Математика – предмет, задачи, изучение, понятие, определения

Математика

Матема́тика (от др.-греч. μάθημα — изучение, наука) — наука о структурах, порядке и отношениях, которая исторически сложилась на основе операций подсчёта, измерения и описания форм реальных объектов [1] . Математические объекты создаются путём идеализации свойств реальных или других математических объектов и записи этих свойств на формальном языке. Математика не относится к естественным наукам, но широко используется в них как для точной формулировки их содержания, так и для получения новых результатов [2] . Математика — фундаментальная наука, предоставляющая (общие) языковые средства другим наукам; тем самым она выявляет их структурную взаимосвязь и способствует нахождению самых общих законов природы [3] .

Содержание

Основные сведения

Идеализированные свойства исследуемых объектов либо формулируются в виде аксиом, либо перечисляются в определении соответствующих математических объектов. Затем по строгим правилам логического вывода из этих свойств выводятся другие истинные свойства (теоремы). Эта теория в совокупности образует математическую модель исследуемого объекта. Таким образом первоначально, исходя из пространственных и количественных соотношений, математика получает более абстрактные соотношения, изучение которых также является предметом современной математики.

Традиционно математика делится на теоретическую, выполняющую углублённый анализ внутриматематических структур, и прикладную, предоставляющую свои модели другим наукам и инженерным дисциплинам, причём некоторые из них занимают пограничное с математикой положение. В частности, формальная логика может рассматриваться и как часть философских наук, и как часть математических наук; механика — и физика, и математика; информатика, компьютерные технологии и алгоритмика относятся как к инженерии, так и к математическим наукам и т. д. В литературе было предложено много различных определений математики (см. ниже).

Этимология

Слово «математика» произошло от др.-греч. μάθημα (máthēma), что означает изучение, знание, наука, и др.-греч. μαθηματικός (mathēmatikós), первоначально означающего восприимчивый, успевающий [4] , позднее относящийся к изучению, впоследствии относящийся к математике. В частности, μαθηματικὴ τέχνη (mathēmatikḗ tékhnē), на латыни ars mathematica, означает искусство математики.

В текстах на русском языке слово «математика» или «мафематика» встречается по крайней мере с XVII века, например, у Николая Спафария в «Книге избранной вкратце о девяти мусах и о седмих свободных художествах» (1672 год) [5]

Определения

Одно из первых определений предмета математики дал Декарт [6] :

К области математики относятся только те науки, в которых рассматривается либо порядок, либо мера и совершенно не существенно, будут ли это числа, фигуры, звёзды, звуки или что-нибудь другое, в чём отыскивается эта мера. Таким образом, должна существовать некая общая наука, объясняющая всё относящееся к порядку и мере, не входя в исследование никаких частных предметов, и эта наука должна называться не иностранным, но старым, уже вошедшим в употребление именем Всеобщей математики.

В советское время классическим считалось определение из БСЭ [7] , данное А. Н. Колмогоровым:

Математика… наука о количественных отношениях и пространственных формах действительного мира.

Это определение Энгельса [8] ; правда, далее Колмогоров поясняет, что все использованные термины надо понимать в самом расширенном и абстрактном смысле.

Сущность математики… представляется теперь как учение об отношениях между объектами, о которых ничего не известно, кроме описывающих их некоторых свойств,— именно тех, которые в качестве аксиом положены в основание теории… Математика есть набор абстрактных форм — математических структур.

Приведём ещё несколько современных определений.

Современная теоретическая («чистая») математика — это наука о математических структурах, математических инвариантах различных систем и процессов [10] .

Математика — наука, предоставляющая возможность исчисления моделей, приводимых к стандартному (каноническому) виду. Наука о нахождении решений аналитических моделей (анализ) средствами формальных преобразований [11] .

Герман Вейль пессимистически оценил возможность дать общепринятое определение предмета математики:

Вопрос об основаниях математики и о том, что представляет собой в конечном счёте математика, остаётся открытым. Мы не знаем какого-то направления, которое позволит в конце концов найти окончательный ответ на этот вопрос, и можно ли вообще ожидать, что подобный «окончательный» ответ будет когда-нибудь получен и признан всеми математиками.

«Математизирование» может остаться одним из проявлений творческой деятельности человека, подобно музицированию или литературному творчеству, ярким и самобытным, но прогнозирование его исторических судеб не поддаётся рационализации и не может быть объективным [12] .

Разделы математики

1. Математика как учебная дисциплина подразделяется в Российской Федерации на элементарную математику, изучаемую в средней школе и образованную дисциплинами:

• арифметика,
• элементарная алгебра
• элементарная геометрия: планиметрия и стереометрия
• теория элементарных функций и элементы анализа

и высшую математику, изучаемую на нематематических специальностях вузов. Дисциплины, входящие в состав высшей математики, варьируются в зависимости от специальности.

Программа обучения по специальности математика [13] образована следующими учебными дисциплинами:

2. Математика как специальность научных работников Министерством образования и науки Российской Федерации [14] подразделяется на специальности:

3. Для систематизации научных работ используется раздел «Математика» [15] универсальной десятичной классификации (УДК).

4. Американское математическое общество (AMS) выработало свой стандарт для классификации разделов математики. Он называется Mathematics Subject Classification. Этот стандарт периодически обновляется. Текущая версия — это MSC 2010. Предыдущая версия — MSC 2000.

Обозначения

Вследствие того, что математика работает с чрезвычайно разнообразными и довольно сложными структурами, система обозначений также очень сложна. Современная система записи формул сформировалась на основе европейской алгебраической традиции, а также математического анализа (понятия функции, производной и т. д.). Геометрия испокон века пользовалась наглядным (геометрическим же) представлением. В современной математике распространены также сложные графические системы записи (например, коммутативные диаграммы), нередко также применяются обозначения на основе графов.

Краткая история

Академиком А. Н. Колмогоровым предложена такая структура истории математики:

1. Период зарождения математики, на протяжении которого был накоплен достаточно большой фактический материал;
2. Период элементарной математики, начинающийся в VI—V веках до н. э. и завершающийся в конце XVI века («Запас понятий, с которыми имела дело математика до начала XVII века, составляет и до настоящего времени основу „элементарной математики“, преподаваемой в начальной и средней школе»);
3. Период математики переменных величин, охватывающий XVII—XVIII века, «который можно условно назвать также периодом „высшей математики“»;
4. Период современной математики — математики XIX—XX века, в ходе которого математикам пришлось «отнестись к процессу расширения предмета математических исследований сознательно, поставив перед собой задачу систематического изучения с достаточно общей точки зрения возможных типов количественных отношений и пространственных форм».

Развитие математики началось вместе с тем, как человек стал использовать абстракции сколько-нибудь высокого уровня. Простая абстракция — числа; осмысление того, что два яблока и два апельсина, несмотря на все их различия, имеют что-то общее, а именно занимают обе руки одного человека, — качественное достижение мышления человека. Кроме того, что древние люди узнали, как считать конкретные объекты, они также поняли, как вычислять и абстрактные количества, такие, как время: дни, сезоны, года. Из элементарного счёта естественным образом начала развиваться арифметика: сложение, вычитание, умножение и деление чисел.

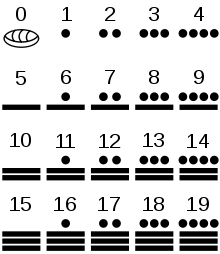
Развитие математики опирается на письменность и умение записывать числа. Наверно, древние люди сначала выражали количество путём рисования чёрточек на земле или выцарапывали их на древесине. Древние инки, не имея иной системы письменности, представляли и сохраняли числовые данные, используя сложную систему верёвочных узлов, так называемые кипу. Существовало множество различных систем счисления. Первые известные записи чисел были найдены в папирусе Ахмеса, созданном египтянами Среднего царства. Индская цивилизация разработала современную десятичную систему счисления, включающую концепцию нуля.

Исторически основные математические дисциплины появились под воздействием необходимости вести расчёты в коммерческой сфере, при измерении земель и для предсказания астрономических явлений и, позже, для решения новых физических задач. Каждая из этих сфер играет большую роль в широком развитии математики, заключающемся в изучении структур, пространств и изменений.

Философия математики

Цели и методы

Математика изучает воображаемые, идеальные объекты и соотношения между ними, используя формальный язык. В общем случае математические понятия и теоремы не обязательно имеют соответствие чему-либо в физическом мире. Главная задача прикладного раздела математики — создать математическую модель, достаточно адекватную исследуемому реальному объекту. Задача математика-теоретика — обеспечить достаточный набор удобных средств для достижения этой цели.

Содержание математики можно определить как систему математических моделей и инструментов для их создания. Модель объекта учитывает не все его черты, а только самые необходимые для целей изучения (идеализированные). Например, изучая физические свойства апельсина, мы можем абстрагироваться от его цвета и вкуса и представить его (пусть не идеально точно) шаром. Если же нам надо понять, сколько апельсинов получится, если мы сложим вместе два и три, — то можно абстрагироваться и от формы, оставив у модели только одну характеристику — количество. Абстракция и установление связей между объектами в самом общем виде — одно из главных направлений математического творчества.

Другое направление, наряду с абстрагированием — обобщение. Например, обобщая понятие «пространство» до пространства n-измерений. «Пространство , при 3″ border=”0″ /> является математической выдумкой. Впрочем, весьма гениальной выдумкой, которая помогает математически разбираться в сложных явлениях». [16]

Изучение внутриматематических объектов, как правило, происходит при помощи аксиоматического метода: сначала для исследуемых объектов формулируются список основных понятий и аксиом, а затем из аксиом с помощью правил вывода получают содержательные теоремы, в совокупности образующие математическую модель.

Основания

Вопрос сущности и оснований математики обсуждался со времён Платона. Начиная с XX века наблюдается сравнительное согласие в вопросе, что надлежит считать строгим математическим доказательством, однако отсутствует согласие в понимании того, что в математике считать изначально истинным. Отсюда вытекают разногласия как в вопросах аксиоматики и взаимосвязи отраслей математики, так и в выборе логических систем, которыми следует при доказательствах пользоваться.

Помимо скептического, известны нижеперечисленные подходы к данному вопросу.

Теоретико-множественный подход

Предлагается рассматривать все математические объекты в рамках теории множеств, чаще всего с аксиоматикой Цермело — Френкеля (хотя существует множество других, равносильных ей). Данный подход считается с середины XX века преобладающим, однако в действительности большинство математических работ не ставят задач перевести свои утверждения строго на язык теории множеств, а оперируют понятиями и фактами, установленными в некоторых областях математики. Таким образом, если в теории множеств будет обнаружено противоречие, это не повлечёт за собой обесценивание большинства результатов.

Логицизм

Данный подход предполагает строгую типизацию математических объектов. Многие парадоксы, избегаемые в теории множеств лишь путём специальных уловок, оказываются невозможными в принципе.

Формализм

Данный подход предполагает изучение формальных систем на основе классической логики.

Интуиционизм

Интуиционизм предполагает в основании математики интуиционистскую логику, более ограниченную в средствах доказательства (но, как считается, и более надёжную). Интуиционизм отвергает доказательство от противного, многие неконструктивные доказательства становятся невозможными, а многие проблемы теории множеств — бессмысленными (неформализуемыми).

Конструктивная математика

Конструктивная математика — близкое к интуиционизму течение в математике, изучающее конструктивные построения [прояснить] . Согласно критерию конструктивности — «существовать — значит быть построенным». [17] Критерий конструктивности — более сильное требование, чем критерий непротиворечивости. [18]

Основные темы

Числа

Понятие «число» первоначально относилось к натуральным числам. В дальнейшем оно было постепенно распространено на целые, рациональные, действительные, комплексные и другие числа.

Числовые системы
Счётные множества	Натуральные числа () • Целые () • Рациональные () • Алгебраические () • Периоды • Вычислимые • Арифметические
Вещественные числа и их расширения	Вещественные () • Комплексные () • Кватернионы () • Числа Кэли (октавы, октонионы) () • Седенионы () • Альтернионы • Процедура Кэли — Диксона • Дуальные • Гиперкомплексные • Суперреальные • Гиперреальные • Surreal number (англ.)
Другие числовые системы	Кардинальные числа • Порядковые числа (трансфинитные, ординал) • p-адические • Супернатуральные числа
См. также	Двойные числа • Иррациональные числа • Трансцендентные • Числовой луч • Бикватернион

Преобразования

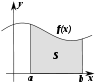
Арифметика	Дифференциальное и интегральное исчисление	Векторный анализ	Анализ
Дифференциальные уравнения	Динамические системы	Теория хаоса

Структуры

Пространственные отношения

Более наглядные подходы в математике.

Дискретная математика

Дискретная математика включает средства, которые применяются над объектами, способными принимать только отдельные, не непрерывные значения.

Математическая логика	Теория вычислимости	Криптография	Теория графов

Коды в системах классификации знаний

• УДК 51
• Государственный рубрикатор научно-технической информации (ГРНТИ) (по состоянию на 2001 год): 27 [19]

Онлайновые сервисы

Существует большое число сайтов, предоставляющих сервис для математических расчётов. Большинство из них англоязычные. [20] Из русскоязычных можно отметить сервис математических запросов поисковой системы Nigma.

Предмет математики

Предмет математики нельзя ни подменять формальными логическими схемами, ни низводить до уровня коллекции разрозненных фактов. Математика есть учение об общих формах, свойственных реальному бытию, она создает постоянно развивающиеся теории, пригодные для самых различных запросов естествознания и техники. Именно это позволяет применять математические методы, разработанные при решении задач одной области науки, к совершенно непохожим на них задачам, относящимся к совсем иным областям знания.

Известны два подхода к определению предмета математики. Одно определение дано Ф.Энгельсом, другое – коллективом французских математиков под общим псевдонимом Н.Бурбаки.

Согласно Ф. Энгельсу, «чистая математика имеет своим объектом пространственные формы и количественные отношения действительного мира, стало быть, – весьма реальный материал. Тот факт, что этот материал принимает чрезвычайно абстрактную форму, может лишь слабо затушевывать его происхождение из внешнего мира». Хотя это предложение нельзя считать полным определением математики, поскольку оно не указывает метод, цели изучения математики, но отражает то, что объект изучения создан умом человека не произвольно, а в связи с реальным миром.

Второй подход отражает методологические установки Н. Бурбаки, которые также определяют не математику, а только объекты, которые она исследует. Прежде чем привести их определение, отметим, что новый подход к объектам исследования в математике связан с «революцией в аксиоматике». Суть ее состоит в переходе от конкретной содержательной аксиоматики к аксиоматике сначала абстрактной, а затем полностью формализованной.

В конкретной содержательной аксиоматике, подобной аксиоматике Евклида, исходные понятия и аксиомы в качестве интерпретации имеют единственную систему хотя и идеализированных, но конкретных объектов. В противоположность этому абстрактная аксиоматика допускает бесчисленное множество интерпретаций. Формализованная аксиоматика возникает на основе абстрактной и отличается, во-первых, точным заданием правил вывода, во-вторых, вместо содержательных рассуждений использует язык символов и формул, в результате чего содержательные рассуждения сводятся к преобразованию одних формул в другие, т. е. к особого рода исчислениям. В соответствии с этим одни и те же аксиомы могут описывать свойства и отношения различных по своему конкретному содержанию объектов.

Эта фундаментальная идея лежит в основе понятия абстрактной структуры. Н.Бурбаки выделяют три основных типа структур, которые играют важную роль при построении ими современной математики.

Алгебраические структуры.Примерами таких структур являются группы, кольца и поля. Основные характеристики алгебраической структуры: задание на некотором множестве А конечного числа операций с соответствующими свойствами, описываемых системой аксиом. В качестве элементов множества А могут выступать как математические объекты (числа, матрицы, перемещения, векторы), так и нематематические.

Структуры порядкахарактеризуются тем, что на рассматриваемом множестве задается отношение порядка (сравнение на числовых множествах), для которого выполняются следующие свойства: рефлексивность, симметричность, транзитивность.

Топологические структуры.Множество М обладает топологической структурой, если каждому его элементу тем или иным способом отнесено семейство подмножеств из М, называемых окрестностями этого элемента, причем эти окрестности должны удовлетворять определенным аксиомам (аксиомам топологических структур). С помощью топологических структур точно определяются такие понятия, как «окрестность», «предел», «непрерывность».

Кроме основных трех типов структур (порождающих), в математике приходится рассматривать сложные структуры, где порождающие структуры органически связываются с помощью объединяющей системы аксиом. Например, множество действительных чисел является сложной структурой, в которую одновременно входят три основные порождающие структуры.

Общей чертой различных понятий, объединенных родовым названием «математическая структура», является то, что они применимы ко множеству элементов, природа которых не определена. Построить аксиоматическую теорию структуры – значит вывести логические следствия из аксиом структуры, отказавшись от каких-либо других предложений относительно рассматриваемых элементов, от всяких гипотез относительно их «природы».

На основе сказанного Н.Бурбаки делают вывод: «В своей аксиоматической форме математика представляется скоплением абстрактных форм – математических структур, и оказывается (хотя по существу и неизвестно почему), что некоторые аспекты экспериментальной действительности как будто в результате предопределения укладываются в некоторые из этих форм».

Итак, по Н.Бурбаки, математика – это «скопление математических структур», не имеющих к действительности никакого отношения. Следует сказать, что этот взгляд на математику разделялся многими учеными, которые считали, что определение Ф. Энгельса устарело.

Накопленный в XVII и XVIII вв. огромный фактический материал привел к необходимости углубленного логического анализа и объединения его с новых точек зрения. Связь математики с естествознанием приобретает все более сложные формы. Новые теории стали возникать не только в результате непосредственных запросов практики, естествознания и техники, но также из внутренних потребностей самой математики. Наиболее важные из них: развитие теории функций, теории групп, связанной с исследованием проблемы разрешимости алгебраических уравнений в радикалах, создание неевклидовых геометрий.

Вторая особенность этого периода развития математики связана со значительным расширением области ее приложений. Если до этого математика применялась в таких разделах физики, как механика и оптика, то теперь ее результаты находят приложение в электродинамике, теории магнетизма, термодинамике. Резко возросли потребности техники в математике: баллистика, машиностроение и др.

Третья особенность математики XIX в. обусловлена усиленным вниманием к вопросам обоснования, критического пересмотра исходных положений (аксиом), построению строгой системы определений и доказательств, а также к критическому рассмотрению логических приемов, употребляемых при этих доказательствах. Г. Рузавин так пишет о математике этого периода: «Если раньше основным предметом ее изучения были метрические количественные отношения между величинами и пространственными формами, то, начиная с середины XIX в. она все больше и больше обращается к анализу взаимосвязей неметрической природы». Такое расширение области исследования математики сопровождалось возрастанием абстрактности ее понятий и теорий.

Революционный переворот во взглядах на математику был связан как раз с ее обоснованием, новым пониманием аксиоматического метода. Открытие в 1826 г. Н.Лобачевским того, что замена пятого постулата Евклида о параллельных его отрицанием («Через точку вне прямой проходит более одной прямой, не пересекающей данную»), и выводы из системы аксиом абсолютной геометрии (где выполняются все аксиомы Евклида, кроме аксиомы параллельности) и аксиомы параллельности Лобачевского не привели к логическим погрешностям.

Это развило столь же стройную и богатую содержанием геометрию, как и геометрия Евклида, послужило толчком в изменении взглядов на математику. Сразу встал вопрос о необходимости обоснования новой геометрии, исследовании ее непротиворечивости (из данной системы аксиом нельзя получить двух взаимоисключающих выводов). В этой связи получает дальнейшее развитие аксиоматический метод: 1) решается проблема непротиворечивости, полноты и независимости системы аксиом; 2) появляется новый взгляд на аксиоматическую теорию как бессодержательную, формально-логическую систему. Решение этих проблем было предложено Д. Гильбертом.

Новый взгляд на аксиоматический метод в корне изменил прежние представления о геометрии как полуэмпирической науке. Из открытий неевклидовых геометрий и построения их интерпретаций следовало, что евклидова и неевклидовы геометрии не представляют непосредственное описание эмпирических свойств реального физического пространства, а являются абстрактными системами утверждений, истинность которых может быть проверена после соответствующей конкретной интерпретации.

Таким образом, подход Н.Бурбаки к определению математики как «скоплению абстрактных, бессодержательных, математических структур» был предопределен новым пониманием аксиоматического метода.

Однако подход Н.Бурбаки встретил и негативное отношение, поскольку они не считали нужным выяснять отношение рассматриваемых структур к действительному миру. Не имея возможности описать различные оценки философов и математиков и позиции Н.Бурбаки, остановимся на точке зрения ведущих отечественных математиков – А.Колмогорова, А.Александрова, В.Гнеденко. Они считают, что во времена Энгельса математика изучала количественные отношения между величинами и пространственными формами. Теперь она поднялась до изучения абстрактных структур и категорий. Но на этом основании нельзя считать, что объект изучения математики стал иным, что вместо количественного аспекта действительного мира математика стала исследовать нечто принципиально иное, что современный этап ее развития не связан с предшествующими этапами.

В действительности дело заключается в том, что качественные изменения, происшедшие в математике, дают ей возможность исследовать количественные отношения глубже и шире. А.Колмогоров приходит к выводу, что круг количественных отношений и пространственных форм, изучаемых математикой, чрезвычайно расширяется: в него входят отношения, существующие между элементами произвольной группы, векторами, операторами в функциональных пространствах, все разнообразие форм пространств любого числа измерений и т.п. При таком широком понимании терминов «количественные отношения» и «пространственные формы» определение математики как науки о количественных отношениях и пространственных формах действительного мира применимо и на современном этапе ее развития.

Эту позицию разделяет и А.Александров: в математике рассматриваются не только формы и отношения, непосредственно абстрагированные из действительности, но и логически возможные, определяемые на основе уже известных форм и отношений. Б. Гнеденко обращает внимание на то, что, хотя любая ветвь современной математики действительно изучает математические структуры, данное Н.Бурбаки определение отнюдь не находится в антагонистических отношениях с определением Ф.Энгельса, а лишь с определенных позиций его дополняет.

Подводя итог сказанному, можно заключить, что подход к определению математики через математические структуры представляет собой выражение определенного этапа математического познания. Математика была и остается определенным «инструментом» познания мира, его пространственных форм и количественных отношений. В настоящее время, как уже отмечалось, этот «инструмент» проникает в изучение все более сложных процессов и явлений, в том числе и неметрической природы. Без осознания этого фундаментального философского, методологического положения не может быть сформировано целостное представление об общей картине мира.

Математика претендует на статус «особой» науки, изначально превышающей все прочие по уровню точности, истинности и непротиворечивости своих фундаментальных положений. В сфере конечных величин математика действительно относительно точна и непротиворечива; этого достаточно для более или менее адекватного количественного моделирования самых различных конечных по размерности предметных областей. Что же касается сферы бесконечного, то здесь у современной математики есть свои противоречия, которые могут быть преодолены лишь совместными усилиями математиков, философов и логиков.

Математика

Именная карта банка для детей
с крутым дизайном, +200 бонусов

Закажи свою собственную карту банка и получи бонусы

План урока:

Что такое математика?

Часто можно услышать высказывание «Математика-царица наук». А существует ли история математики, и что же это за наука? Так ли она необходима в современном мире?

Любой из нас ежедневно выполняет множество действий, которые неразрывно связаны с математикой, но даже не догадывается об этом. Посмотрите вокруг – компьютеры, телефоны, кондиционеры, телевизоры, но для правильного использования домашней техники необходимы знания, связанные с математикой. Идем дальше – магазины, спортивные секции, танцевальные занятия, увлечение литературой также нельзя представить без использования математики. Математические знания облегчают жизнь и делают её насыщенной.

Давайте разберемся, что такое математика:

Дословный перевод с греческого утверждает, что математика – это наука или изучение. Более точное определение поясняет, что это наука, изучающая величины, числовые отношения и формы.

В школьном курсе изучения представлены такие разделы математики:

В основе изучения математики лежит ряд математических понятий и действий, без понимания которых невозможно выполнять простейшие вычисления.

Понятие числа. Виды чисел

В понятие числа входит обозначение количественного состава чего-либо.Это одно из главных определений в математике. Каждый вид числа появлялся в результате необходимости выполнения человеком тех или иных расчетов. В связи с необходимостью владеть информацией о количестве предметов, появилось понятие натурального числа и бесконечности ряда натуральных чисел. Необходимость измерения площадей, длин, объемов – породила рациональное число. Для решения сложных уравнений ввели комплексные числа.

• Натуральные числа – это числа, получаемые при определении количества 1,2,3. Множество таких чисел принято обозначать буквой N. Например: 1,2,3 …..
• Целые числа. Определение понятия формулируется так: множество натуральных, отрицательных чисел и нуль. Их принято обозначать буквой Z. Например: -2,-1,0,1,2,3,4…..
• Рациональные числа. В понятие рационального числа входят дроби m/n, где n≠0, при этом m – целое число, а n – натуральное. Обозначаются буквой Q. Например: 2/3, -4/5
• Действительные. В понятие действительного числа включены рациональные и иррациональные числа, которые могут записываться в виде обычной и десятичной конечной и бесконечной дробей, а также нуль. Обозначаются буквой R. Например: 1245, 5⅔, -648,35
• Простыми называют натуральные числа, которые можно представить в виде двух множителей – единицы и самого этого числа. Обозначается буквой Р. Например: 1,3,7,11….
• Также существуют Иррациональные числа – это числа, не являющиеся рациональными, то есть нельзя представить в виде дроби m/n, где n≠0, при этом m – целое число, а n – натуральное. Например, число пи=3,1415926535, число e=2.718281828, квадратный корень из 3 и так далее.

Классы и разряды чисел

Если число представлено в виде одной цифры (5,9), то оно называется однозначным, в виде двух (24,31), трех (211,984) цифр – двузначным, трехзначным, а далее (1893,100561) просто многозначными.

Все существующие цифры сгруппированы по классам и разрядам натуральных чисел. Место цифры в записи числа называют разрядом. Самый маленький разряд – разряд единиц, за ним следует разряд десятков, сотен, тысяч.

При этом число разрядов в классе равняется 3. Самым большим числом класса единиц является 9, а самым большим числом класса тысяч 999999.

Математические действия

Существование математики невозможно без выполнения математических действий. Всего существует 4 вида арифметических действий:

Порядок выполнения математических действий в выражениях со скобками и без скобок

Так же имеется определенный порядок математических действий, запомнив который с легкостью можно решать задания любой сложности. Этот порядок зависит от наличия скобок и предложенных действий:

При отсутствии скобок, действия выполняются в обычном порядке. Вот правильный порядок математических действий в примере без скобок:

1 действие: 24+16=40

2 действие: 40-5=35

В любом выражении первыми необходимо выполнить умножение или деление в порядке очереди. Вот правильный порядок арифметических действий без скобок:

1 действие: 4×5=20

2 действие: 40-20=20

3 действие: 20+50=70

Когда выражение содержит скобки, первыми вычисляются действия в скобках, а потом по порядку все остальные. Вот необходимый порядок математических действий в примере со скобками:

2 действие: 10_2=5

3 действие: 5+5=10

Все очень просто. Если сразу запомнить не получается, то можно пользоваться этим уроком, как шпаргалкой!

Следующий интересный момент заключается в том, что любой компонент математического действия имеет свое название:

Правила нахождения неизвестного компонента при выполнении математических действий

Для того, чтобы максимально упростить решение задач и уравнений, существуют специальные правила нахождения неизвестного компонента:

– для нахождения одного из слагаемых необходимо от суммы отнять второе слагаемое:

-для нахождения уменьшаемого достаточно найти сумму разности и вычитаемого:

-для нахождения вычитаемого, нужно от уменьшаемого отнять разность

– для нахождения множителя, необходимо найти частное произведения и второго множителя

– для нахождения неизвестного делимого, необходимо найти произведение делителя и частного

– для нахождения неизвестного делителя, необходимо делимое разделить на частное

Основные законы выполнения действий (перместительный, сочетательный, распределительный)

Чтобы правильно и быстро выполнять любые арифметические действия всегда нужно помнить их основные законы, которые упрощают даже самый сложный процесс вычислений:

Переместительный закон для действий сложения и умножения.

Сформулируем переместительный закон сложения: при перестановке слагаемых сумма остается прежней.

Запишем равенство, выражающее переместительный закон сложения a+b=b+a

21+39=60 или 39+21=6015×3=45 или 3×15=45

Использование переместительного закона умножения.

Давайте сформулируем переместительный закон умножения: в случае перестановки множителей произведение остается прежним.

Запишем равенство, выражающее переместительный закон умножения a*b=b*a

11×8=88 или 8×11=88

Применение сочетательного закона в сложении.

Давайте сформулируем сочетательный закон сложения: чтобы сложить число и сумму чисел достаточно найти сумму этого числа и любого слагаемого, и к ней прибавить второе слагаемое.

Запишем равенство, выражающее сочетательный закон сложения a+(b+c)=(a+b)+c=a+b+c

Примеры сочетательного закона сложения:

20+(60+10)=90 или 20+(60+10)=90 или 20+(60+10)=20+60+10=90

1 действие: 60+10=70 1 действие: 20+60=80

2 действие: 20+70=90 2 действие: 80+10=90

Использование сочетательного закона умножения.

Этот закон также распространяется и на действие умножение. Давайте сформулируем сочетательный закон умножения: если необходимо, выполнить умножение числа на произведение чисел, то можно любые два множителя заменить их произведением a×(b×c)=(a×b)×c=a×b×c

Применение распределительного закона.

Давайте разберемся, что такое распределительный закон и как он формулируется. Вот формулировка распределительного закона сложения: для умножения числа на сумму, необходимо найти произведения этого числа с одними вторым слагаемыми, а результаты сложить.

Запишем равенство, выражающее распределительный закон a×(b+c)=ab+ac

В случае, когда вычитаемое меньше или равно уменьшаемому, можно использовать распределительный закон для нахождения произведения числа и разности чисел. Для умножения числа на разность, необходимо сначала умножить на уменьшаемое, после на вычитаемое и найти разность полученных произведений. В буквенном виде записывается так: a×(b-c)=a×b-a×c, если b≥c

Достаточно понять или запомнить эти простые законы и тогда любые задачи или уравнения будут казаться очень простыми и интересными, а уроки математики станут любимыми.

Интересные сведения из истории возникновения математики

Откуда же взялась математика? Куда же уходит корнями история развития математики? Самым первым источником появления простейшей математики ученые считают пальцы на руках и ногах, а также различные части тела. Об этом свидетельствует множество наскальных рисунков, дошедших до нашего времени. Учеными установлено, что 6 тысяч лет назад древние вавилоняне уже использовали простые математические действия: для бытовых нужд, учета скота, подсчета количества урожая, размера прибыли и расходов, при совершении купли или продажи различных товаров. Позже они же первые упоминают о решении математических задач и уравнений повышенной сложности. К самым первым математическим открытиям относят возникновение математических действий, которые известны нам как сложение, вычитание, умножение и деление.

Ученые-историки до сих пор спорят о точной дате появления этой науки и о месте, где впервые она появилась. Конкурентами в этом споре выступают древний Вавилон и Египет. Самые первые подтверждения математической деятельности принадлежат Свазиленду. Там найдены кости бабуинов с нанесенными черточками, которые явно говорят о первых математических операциях, выполненных 40000 лет назад.

А когда же появились дроби? Упоминания о дробях возникли гораздо позже, но уже достоверно известно, что жители древнего Египта совершали операции с дробями, у которых числителем являлась единица.

А вот представление о десятичных дробях появилось всего лишь пять столетий назад, а в Европу попало только через 200 лет после появления.

Невероятные факты, связанные с математикой:

• Всю математическую науку возможно записать в сто тысяч томов;
• Центилион – самое большое известное число, содержащее шестьсот нулей;
• Наименьшее число используется только в астрономии. Названия не имеет. Записывается дробью; после запятой имеет сто миллионов триллионов нулей, а в конце единицу;
• Самая магическая цифра, которая таит множество суеверий – 666. В Европейской палате все время пустует только одно кресло под номером 666. Во всем мире люди стараются не использовать это число. Такой номер не присваивается телефонным кодам, автобусам,трассам или поездам;
• В Китае самым суеверным числом считают число 4. При этом, такой номер не присваивается домам, квартирам, нет даже 4 этажа.

Математика очень дружна со всеми существующими науками, видами деятельности и профессиями. Одно мудрое выражение гласит «Математика-язык других наук». Поспорить с этим очень сложно, ведь она является основой для развития таких дисциплин:

• Химия;
• Физика;
• Астрономия;
• Биология;
• История;
• Экономика;
• География;
• Информатика;
• Политология;
• Музыка;
• Литература.

Теперь мы можем с уверенностью сказать, что знание математики – залог вашей успешности и развития не только в будущем, а уже сегодня!

Математика как наука: предмет, методы, понятия

Число — важнейшее понятие математики. Содержание его меня­лось на протяжении веков. В связи со счетом возникло понятие о целых положительных числах (натуральных), а затем Евклид и Ар­химед (III в. до н.э.) ввели понятие бесконечности натурального ряда чисел. Индийцы изобрели цифры для записи натурального числа при помощи десяти знаков.

Задачи измерения длин, площадей, где предполагалось выде­ление долей, привели к понятию рационального (дробного) чис­ла — числа вида т/п, где тип — целые числа и п * 0. Понятие отри­цательного числа возникло у индийцев в VI—XI вв. Потребность в точном выражении отношений величин (например, отношение диагонали квадрата к его стороне) привела к введению иррацио­нальных чисел. В Древней Греции были зафиксированы иррацио­нальные отношения (отношения несоизмеримости), но они еще не имели статуса чисел. Иррациональные числа представлены бесконечными непериодическими десятичными дробями и выра­жаются через рациональные приближенно.

В связи с решением квадратных и кубических уравнений в XVI в. были введены комплексные числа вида х + />, где х и у — дей­ствительные числа, /— мнимая единица. Вместе с ними возникло понятие мнимого числа. Для многих крупных ученых XVII в. алгеб-

раическая и геометрическая сущность мнимых величин представ­лялась неясной, загадочной и даже мистической. Г. Лейбницу принадлежит фраза: «Мнимые числа – это прекрасное и чудесное убежище божественного духа, почти что амфибия бытия с небы­тием». В физике закономерности микромира описываются ком­плексными величинами. Математический язык благодаря боль­шой емкости, точности и гибкости позволяет выражать отноше­ния, выходящие за рамки наглядных представлений.

о высокой степенью абстрактности ее понятий (точки без размеров, линии без толщины, множества любых предметов);

0 высокой степенью их общности (например, в алгебре буква обо­значает любое число, в математической логике рассматриваются произвольные высказывания и т.д.).

Абстрактность и общность понятий математики позволяют один и тот же математический аппарат применять в различных науках.

Предметом математики являются системы математических объектов. При этом под системой понимается множество объек­тов с множеством отношений, существующих между этими объек­тами.

Математическими объектами называются абстрактные идеа­лизированные объекты. Математические объекты играют важную роль в формировании математических теорий.

Абстрактный объект — это объект, наделенный теми свойства­ми, которые содержатся в его определении. Математика исследует формы и отношения, полностью отвлеченные от содержания, со­храняя в них лишь то, что содержится в их определениях. В связи с этим результаты в математике получаются путем логических вы­водов из самих этих определений, так что чистая математика име­ет дедуктивный умозрительный характер.

Математические объекты не просто абстрактные объекты, но еще и идеализированные объекты (т.е. определены посредством признаков, доведенных «до предела»). Доведение определенных признаков «до предела», «до абсолюта» называется идеализацией. В математике идеализация состоит в доведении количественных характеристик реальных объектов до нуля или до бесконечности.

Предмет математики в действительном мире представляет со­бой пространственные формы и количественные отношения дей­ствительного мира. Отсюда возникает вопрос: каким способом выделить количественные отношения в чистом виде, т.е. как опи­сать их так, чтобы это описание не зависело от содержания объек­тов. Примеры количественных отношений действительного мира общеизвестны.

В истории развития математики постепенно формировались ее основные методы — анализ и синтез, индукция и дедукция, обобщение и абстрагирование, аналогия и различные типы аксио­матик (содержательная, полуформальная и формальная).

Методы выделения формы в чистом виде весьма разнообраз­ны. Для этого применяются логико-математические языки. При этом существенное значение имеет аксиоматический метод.

Аксиоматический метод предполагает описание количествен­ных отношений без учета специфики объектов, между которыми эти отношения имеют место. Существенной чертой этого метода является то, что в аксиоматической теории все термины разделя­ются на исходные и производные, а предложения на недоказуе­мые (аксиомы) и доказуемые (теоремы). Доказательство теорем основывается на формальнологической дедукции, или выводе их из аксиом с помощью правил логики. В зависимости от подразде­ления аксиом математических теорий и их логик на содержатель­ные и формальные выделяют три вида аксиоматик – содержа­тельные, которые имеют содержательные аксиомы математиче­ской теории и неформализованную логику (например, евклидова геометрия в изложении самого Евклида), полуформальные, кото­рые имеют формальные аксиомы и неформализуемую интуитив­ную логику (например, евклидова геометрия в том виде, как ее представил Д. Гильберт в книге «Основания геометрии»), и пол­ностью формальные, содержащие формальные аксиомы как собст­венно математической теории, так и логики.

Хотя математика является единой системой знаний, она под­разделяется на теоретическую (чистую) и прикладную. В рамках теоретической математики принято различать содержательное и формальное знание. К содержательной математике относятся теории, изучающие системы абстрактных математических объек­тов (числовые системы, алгебраические системы, системы гео­метрических фигур и т.д.). К формальной математике принадле­жат формальные теории (исчисление), предложения и термины которых не обязательно связаны с интерпретацией, т.е. с их зави­симостью от эмпирических или абстрактных систем объектов.

В истолковании предмета математики выделяют три аспек­та – синтаксический, семантический и прагматический. Фунда­ментальной характеристикой математического познания являет­ся доказательство.

Итак, возрастание роли математики и ее методов является од­ной из важнейших характеристик науки XX и XXI вв. Логика при этом выступает и как метод математики, и как математическая теория [2].

1. Математика // Энциклопедия книжного клуба XXI века. М., 2002. Т. И.

2. Перминов В.Я. Философия и основания математики. М., 2002.

Методика изучения математических понятий

Методика изучения математических понятий

1. Сущность понятия. Содержание и объем понятия.

2. Определение математических понятий.

3. Классификация математических понятий.

4. Методика введения новых математических понятий.

Любая наука представляет собой систему понятий, поэтому в математике, как и в других учебных предметах, уделяется значительное внимание обучению понятиям. Понятие относится к формам теоретического мышления, которое является рациональной ступенью познания.

1. Сущность понятия. Содержание и объем понятия. При помощи понятий мы выражаем общие, существенные признаки вещей и явлений объективной действительности.

Восприятием называется непосредственное чувственное отражение действительности в сознании человека.

Представлением называется запечатленный в нашем сознании образ предмета или явления, в данный момент нами не воспринимаемого.

Восприятие исчезает как только воздействие предмета на органы чувств человека кончается. Остается представление. Например, показываем куб, а потом его убираем. Мы знаем различные кубы, разного цвета и т. п., но мы от этого отвлекаемся, сохраняя общее и существенное.

Понятие абстрагируется от индивидуальных черт и признаков отдельных восприятий и представлений и является результатом обобщения восприятий и представлений очень большого количества однородных предметов и явлений, например: число, пирамида, окружность, прямая. Понятия образуются путем таких логических приемов, как анализ и синтез, абстрагирование и обобщение. Понятием будем называть мысль о предмете, выделяющую его существенные признаки.

Существенными признаками понятия называются такие признаки, каждый из которых необходим, а все вместе достаточны, чтобы отличить объекты данного рода от других объектов (например, параллелограмм).

В каждом понятии различают его содержание и объем.

Содержанием понятия называется совокупность существенных признаков объектов, охватываемых понятием. Основное содержание – достаточный набор свойств, т. е. все те свойства, каждое их которых, взятое отдельно, необходимо, а взятые в совокупности достаточны для отличения данного понятия от остальных.

Объемом понятия называется совокупность объектов, на которое распространяется данное понятие.

Например, понятие «человек». Содержание: живое существо, создает орудия производства, обладает способностью абстрактного мышления. Объем: все люди.

Понятие «тетраэдр». Содержание: многогранник, ограниченный четырьмя гранями, имеющими форму треугольников. Объем: множество всех тетраэдров.

Между объемом и содержанием понятия существует соотношение: чем больше содержание понятия, тем меньше его объем. Сокращение содержания понятия влечет за собой расширение его объема. Эту операцию называют обобщением понятия. Например, если из содержания понятия «равносторонний треугольник» изъять свойство «равенство всех сторон», то множество треугольников, удовлетворяющих новому содержанию, станет «шире» – будет содержать множество равносторонних треугольников в качестве подмножества. Расширение содержания понятия ведет к сужению его объема и называется ограничением (специализацией) понятия. Пример такой операции – переход от понятия тождественных преобразований к понятию сокращение дробей.

Если объем одного понятия входит как часть в объем другого понятия, то первое понятие называется видовым, а второе – родовым.

Понятия род и вид имеют относительный характер. Например, понятие «призма» является родовым по отношению к понятию «прямая призма», но видовым понятием по отношению к понятию «многогранник».

2. Определение математических понятий. Содержание понятия раскрывается с помощью определения.

Определение (дефиниция) понятия – это такая логическая операция, при помощи которой раскрывается основное содержание понятия или значение термина.

Определить понятие – это значит перечислить существенные признаки предметов, отображенных в данном понятии.

Задача перечисления признаков бывает нелегкой, но она упрощается, если опираться на понятия, ранее уже установленные. Понятие фиксируется в речи с помощью слова или словосочетания, называемого именем или термином понятия. В математике понятие часто обозначается не только именем, но и символом. Например, и другие.

Таким образом, в определении сначала указывается род, в который определяемое понятие входит как вид, а затем указывают те признаки, которые отличают этот вид от других видов ближайшего рода. Такой прием определения понятия называется определением понятия через ближайший род и видовое отличие.

Понятие = род + видовое отличие.

Через род и видовые

отличия Аксиоматические Описательные

Явными называются определения, в которых смысл определяемого термина полностью передается через смысл определяющих терминов, т. е. явные определения содержат прямое указание на существенные признаки определяемого понятия. Определение через ближайший род и видовое отличие относится к явным.

В неявных определениях смысл определяемого термина не передается полностью определяющими терминами. Пример неявного определения – определение исходных понятий с помощью системы аксиом. Такие определения называются аксиоматическими. Примеры аксиоматических определений являются определения группы, кольца и поля и т. п. (аксиоматика Гильберта, Вейля, система аксиом Пеано для натуральных чисел).

Генетическим называется определение объекта путем указания способа его построения, образования, происхождения. Например, «усеченный конус есть тело, происходящее от вращения прямоугольной трапеции вокруг стороны, перпендикулярной к основаниям трапеции». Или определение понятия «линейный угол двугранного угла».

В индуктивном (рекуррентном) определении объект задается как функция от натурального числа . Это задание обеспечивается указанием значения и некоторого равенства, связывающего значения и. Например, по индукции в математике вводится определение натурального числа.

Остенсивные определения понятий и описательные описывают объекты с помощью моделей, рассмотрения частных случаев, выделения отдельных существенных свойств, вводятся с помощью непосредственного показа, демонстрации предметов. Часто применяются в начальных классах и частично в 5-6 классах. Учитель, изображая треугольники на доске, знакомит учащихся с понятием треугольник. В средней школе преобладают вербальные определения.

Чтобы дать логически правильное определение, нужно соблюдать правила определения:

1. Определение должно быть соразмерным, то есть определяемое и определяющие понятия должны быть равны по объему. Чтобы проверить соразмерность, нужно убедиться, что определяемое понятие удовлетворяет признакам определяющего понятия и наоборот.

Например, дано определение: «Параллелограмм есть многоугольник, у которого противоположные стороны параллельны». Проверим его: «Всякий многоугольник, у которого противоположные стороны параллельны, есть параллелограмм» – это неверно. Или: «параллельными прямыми называются прямые, которые не пересекаются» (неверно, это могут быть и скрещивающиеся прямые).

2. Определение не должно содержать в себе «порочного круга». Это означает, что нельзя строить определение таким образом, чтобы определяющим понятием было такое, которое само определяется при помощи определяемого понятия.

Например, «прямым углом называется угол, содержащий , а градусом называется 1/90 часть прямого угла». Иногда «порочный круг» принимает форму тавтологии (то же посредством того же) – употребление слова, имеющего то же самое значение.

3. Определение по возможности не должно быть отрицательным. В определение должны указываться существенные признаки предмета, а не то, чем не является предмет.

Например, «ромб – это не треугольник», «эллипс – это не окружность». В математике в некоторых случаях отрицательные определения допустимы, например, «трансцендентной функцией называется всякая неалгебраическая функция».

4. Определение должно быть четким и ясным, не допускающим двусмысленных или метаморфических выражений.

Например, «арифметика есть царица математики» – образное сравнение, а не определение, утверждение «лень – мать всех пороков», поучительно, но не определяет понятие лени.

3. Классификация математических понятий. Объем понятия раскрывается путем классификации. Классификация – это систематическое распределение некоторого множества по классам, возникающее в результате последовательного деления, основанного на сходстве объектов одного вида и отличии их от объектов других видов.

Операция деления – логическая операция, раскрывающая объем понятия путем выделения в нем возможных видов объекта. Например, всех студентов педагогического университета можно разделить на собирающихся идти работать в школу и не собирающихся. Основанием деления является свойство, в соответствии с которым выделяются виды. В нашем примере основанием является свойство: «иметь намерение работать в школе».

При осуществлении классификации важен выбор основания: разные основания дают разные классификации. Классификация может производиться по существенным свойствам (естественная) и по несущественным (вспомогательная). При естественной классификации, зная к какой группе принадлежит элемент, можем судить о его свойствах.

Два вида деления:

1. деление по видоизменению признака – это деление, при котором свойство – основание деления присуще объектам выделенных видов в разной степени

2. дихотомическое деление – это деление, при котором данное понятие делится на два вида по наличию или отсутствию некоторого свойства.

Операция деления подчиняется следующим правилам:

1. деление должно быть соразмерным, т. е. объединение выделенных классов должно образовывать исходное множество (сумма объемов видовых понятий равна объему родового понятия).

2. деление должно проводится только по одному основанию.

3. пересечение классов должно быть пусто.

4. деление должно быть непрерывным.

4. Методика введения новых математических понятий. В методике преподавания математики выделяются два метода введения понятий: конкретно-индуктивный и абстрактно-дедуктивный (термины введены русским методистом ).

Схема применения конкретно-индуктивного метода.

1. Рассматриваются и анализируются примеры (анализ, сравнение, абстрагирование, обобщение,…).

2. Выясняются общие признаки понятия, которые его характеризуют.

3. Формулируется определение.

4. Определение закрепляется путем приведения примеров и контрпримеров.

5. Дальнейшее усвоение понятия и его определения проходит в процессе их применения:

а) распознавание понятия.

б) конструирование (нарисовать).

в) применение данного определения к решению задач.

Например, понятие параллелограмма.

Пример. Введение понятия – вертикальные углы.

Задания: 1. нарисуйте угол

2. постройте лучи и , противоположные данным.

3. какую фигуру образуют лучи и .

4. углы и называются вертикальными.

5. попробуйте дать определение вертикальных углов.

6. нет ли на рисунке еще вертикальных углов.

7. назовите вертикальные углы.

8. как нарисовать два вертикальных угла.

Схема применения абстрактно-дедуктивного метода.

Формулируется определение понятия. Приводятся примеры и контрпримеры. Закрепляется понятие путем выполнения различных упражнений.

Например, введение квадратного уравнения, понятия декартовых координат и т. п.

При формировании понятий целесообразно применять рекомендации психолого-педагогических наук, например, теорию поэтапного формирования умственных действий .

1 этап. Разъясняют цель вводимого понятия, дают ориентировку.

2 этап. Учащиеся формулируют определение исходя из рисунка.

3 этап. Учащиеся формулируют определение, пользуясь громкой (внешней) речью без опоры на рисунок.

4 этап. Определение проговаривается в форме внешней речи про себя.

5 этап. Определение проговаривается в форме внутренней речи.

При изучении понятий надо варьировать несущественные признаки (принципы варьирования) – это разнообразное расположение на доске рисунков и чертежей, например, треугольника, его высоты, перпендикуляра к прямой и т. д. (не только горизонтальное расположение прямой, основания треугольника и т. п.)

Усвоению определений помогает анализ логической структуры определения. С этой целью составляются алгоритмы распознавания понятий, математические диктанты и тесты.

Предмет математики

Предмет математики — то, что изучает математика как наука, выраженное в наиболее общей форме. Одно из возможных определений предмета математики — это изучение систем математических объектов. Проблема определения предмета математики тесно связана с проблемой определения самой математики и ее сути, что она из себя представляет.

Существуют различные подходы к определению предмета математики. В частности, в литературе высказывается мнение, что предмет математики менялся на протяжении ее развития. При этом достаточно актуальными остаются мысли, высказанные древнегреческими философами.

Содержание

[править] Математические объекты

Математика непосредственно изучает системы математических объектов. Эти объекты определяются в рамках самой математики (базовые объекты — через системы аксиом). Проблема их связи с объективной реальностью («априорность математики») не имеет однозначного разрешения и выходит за рамки математики (изучается в философии математики). Математические объекты возникают как результат человеческого мышления и не существуют в объективной реальности (согласно концепциям идеалистической философии, восходящим к Платону, математические объекты существуют в умопостигаемом мире или «мире идей»). Ф. Энгельс писал в «Диалектике природы»: «…вся так называемая чистая математика занимается абстракциями… все её величины суть, строго говоря, воображаемые величины…». Идеализированные объекты появляются и в других науках, но в них они сохраняют большее сходство с реальностью, в математике их подобие объективной реальности минимальное. Математика изучает системы отношений между математическими объектами, которые также не существуют в материальном мире. Тем не менее, ряд математических теорий находит приложения в качестве основы для моделей процессов реального мира, что является основой развития ряда современных наук — см. Математизация научного знания.

[править] Определения классиков

Существует ряд классических определений математики, актуальных до сих пор.

Одно из первых определений предмета математики дал Рене Декарт [1] :

Лейбниц связал математику с воображением и логикой.

Определение Лейбница стало основой логицизма (философского подхода к математики, развивавшегося в XX веке).

Подход Канта воплотился в интуиционизме.

Другие определения и цитаты, раскрывающие суть математики от ее классиков:

Как обоснование того, что невозможно дать окончательное определение математики на все времена, высказывается довод, что любое определение математики заключает ее в какие-то границы, а математика может обобщить и изменить любую схему, поэтому такое определение обречено быть некорректным.

В советских энциклопедиях обычно приводится определение математики, данное классиком марксизма Фридрихом Энгельсом:

Чистая математика имеет своим объектом пространственные формы и количественные отношения действительного мира

Это определение также не может быть окончательным, так как математика может изучать отношения, не являющиеся ни пространственными, ни количественными. По мнению А. Н. Колмогорова, определение Энгельса нуждается лишь в такой модернизации:

Математика — это наука о количественных отношениях и пространственно-подобных формах во всей их общности.

Во многих из определений математики, речь идет только «чистой» математике, в то же время сейчас считается, что математика включает как чистую и прикладную части, так и метаматематику (совокупность формализуемых представлений о математике).

Прикладной математикой согласно одному из подходов, можно считать совокупность теорий о системах объективной действительности и мышления, полученных интерпретацией теорий чистой математики.

Метаматематика — теория, изучающая синтаксические (формальные), семантические (содержательные) и логические свойства теорий чистой математики, то есть метаматематика занимается непротиворечивостью математических теорий и математики в целом, их полнотой, независимостью систем аксиом.

В. Н. Третьяков в своей дипломной работе «О философских проблемах математики» (Минск, 1978 г.) попытался подытожить определения классиков так:

Математика — это наука, занимающаяся построением теорий о количественных отношениях и пространственно-подобных формах во всей их общности, разрабатывающая интерпретации этих теорий на объекты действительности и проверяющая их состоятельность с точки зрения формы и содержания.

[править] Проблема обоснования математики

С появлением все новых и более абстрактных математических теорий с XIX века появился вопрос об их обосновании. Довольно очевидно, что проверить опытным путем такие теории нельзя. Поэтому обоснование математических теорий стало пониматься как получение доказательства их непротиворечивости и полноты. От работ Георга Кантора идет перевод оснований математики на язык теории множеств. Однако теория множеств столкнулась с некоторыми логическими парадоксами, что привело к необходимости пересмотра логических оснований математики.

Другим подходом к обоснованию математики стала попытка сведения математики к логике (работы Бертрана Рассела, Уайтхеда, Фреге). Появившееся в результате течение под названием «логицизм» ограничивало идеализацию и запрещал вводить такие объекты, приводящих к парадоксам в теории множеств.

Давид Гильберт предложил программу доказательства непротиворечивости математики под названием «формализм». В рамках данного подхода предполагалось последовательно формализовать все содержательные математические теории и свести обоснование теорий к доказательству непротиворечивости формы. Однако теоремы Гёделя показали, что на этом пути получить формальное доказательство непротиворечивости математики невозможно (так называемыми «финитными методами»). Тем не менее, позднее появились нефинитные доказательства непротиворечивости математики.

Еще один подход к обоснованию математики под названием «интуиционизм», восходящий к Брауэру, Вейлю и др., вводит критерий интуитивной ясности для оценки математических суждений. В рамках этого подхода также предлагается ограничивать идеализацию, например, предлагалось исключать из рассмотрения актуально бесконечные множества.

В 1945 году С. К. Клини предложил новый вариант интуиционистского понимания арифметических суждений, основанный на развитой в 1930-е годы теории алгоритмов и получивший известность под именем рекурсивной реализуемости. Дальнейшая разработка данного подхода и связанных с ним идей в научной школе А. А. Маркова привела к возникновению современной конструктивной математики.

Проблема обоснования математики остаётся открытой вплоть до настоящего времени. Существует скептический подход к возможности ее окончательного разрешения.

Понятие «задача». Подходы к классификации математических задач

Содержательный компонент методики обучения математике состоит из теоретического материала и практической части – задач. Причём усвоение теоретического материала происходит именно в процессе решения соответствующих задач. Математик и популяризатор науки Дж.Пойа писал о задачах: «Что значит владение математикой? Это есть умение решать задачи, причём не только стандартные, но и требующие известной независимости мышления, здравого смысла, оригинальности, изобретательности».

Определение понятия «задача»

Термин «задача» в повседневной жизни понимается как проблема, требующая решения, или как проблемная ситуация. В этом понимании задачи присутствуют в жизни человека на всех уровнях.

В рамках математической науки задачи соседствуют с понятиями и определениями, алгоритмами, теоремами и т.д. При этом задачи занимают особое место, так как все теоретические знания усваиваются посредством решения задач.

Очевидно, что задачи являются одним из главных компонентов содержания учебного предмета математики. По этой причине нужно с особым вниманием подойти к определению понятия задачи.

В общих чертах задача понимается как цель, поставленная в определённых условиях. Л.Л. Гурова ставит во главу угла умственные усилия человека, прилагаемые в процессе решения задачи: «Задача – объект мыслительной деятельности, содержащий требования некоторого практического преобразования или ответа на теоретический вопрос посредством поиска условий, позволяющих раскрыть связи (отношения) между известными и неизвестными её элементами».

Понимание задачи как определённой системы обнаруживается в работах Г.А.Балл, Ю.М.Колягина, Л.М.Фридмана, А.Ф.Эсаулова и др. Г.А.Балл определяет задачу как «систему, обязательными компонентами которой являются:

а) предмет задачи, находящийся в исходном состоянии;

б) модель требуемого состояния предмета задачи (эту модель мы отождествляем с требованием задачи).

Л.М.Фридман отсылает к пониманию задачи как проблемной ситуации: «Генезис задачи можно рассматривать как моделирование проблемной ситуации, в какую попадает субъект в процессе своей деятельности, а саму задачу – как модель проблемной ситуации, выраженной с помощью знаков некоторого естественного или искусственного языка».

Структура задачи

Учитывая разнообразие трактовок, можно обозначить структурные элементы задачи как объекта мыслительной деятельности:

1. Условие (У) – предметная область задачи (объекты) и отношения между объектами.
2. Обоснование (О) – теоретические или практические основания для перехода от условия к заключению посредством операций, которые составляют решение задачи, т.е. базис задачи.
3. Решение (Р) – совокупность действий или операций, которую необходимо произвести над известными компонентами, чтобы выполнить требование, сформулированное в заключении,– оператор задачи.
4. Заключение (З) – требование отыскать неизвестные компоненты, убедиться в правильности чего-либо, доказать, сконструировать и т.д.

Термин «решение задачи» в современной практике обучения может иметь несколько трактовок:

• решение задачи как план (способ, метод) осуществления требования задачи;
• решение задачи как процесс выполнения плана, требования задачи;
• решение задачи как результат выполнения плана решения задачи.

Классификации задач

1. По уровню проблемности.

Процесс решения задач зависит от ряда субъективных факторов. Так, Ю.М.Колягин классифицировал задачи по признаку проблемности:

Стандартные задачи: решающему известны все компоненты задачи (условие (У); обоснование (О); решение (Р); заключение (З). Именно такие задачи реализуются на этапе усвоения теоретического материала. Данный тип задач позволяет не только закрепить полученные теоретическое знания, но и проверить уровень понимания, осуществить обратную связь. Так, на этапе усвоения теоретического материала после введения теории (определения, понятия, правила) учитель может использовать задачи на распознавание: относится тот или иной объект к введенному понятию.

Обучающие задачи: один компонент неизвестен – х. Тогда задача схематично может выглядеть так: УОРх, УОхЗ, УхРЗ, хОРЗ.

Рассмотрим примеры задач данного типа:

Дано: 2х 2 + х 2 – 5 = 0. Используя формулу нахождения квадратных корней, найдите х.

Витя нашёл корни квадратного уравнения, применив теорему, обратную теореме Виета. Объясните, как он это сделал.

Маша определила корни квадратного уравнения, разложив его на множители. Назовите математический факт, положенный в основу такого уравнения.

Задача 4. (хОРЗ) Корни квадратного уравнения равны 1 и -1. Они получены с использованием формулы разности квадратов. Составьте соответствующее корням квадратное уравнение.

Поисковые задачи: неизвестны два компонента х и у. Тогда задача схематично выглядит так: УхуЗ, УОху, хуРЗ, УхРу, хОуЗ.

Рассмотрим примеры задач данного типа:

Света изучает математику в кружке. Среди школьников в этом кружке 94% процента мальчиков. Установите наименьшее возможное количество учеников в кружке.

Проблемные задачи: неизвестны три компонента х, у, z. Тогда задача схематично выглядит так: Ухуz, xОуz, хуРz, xyzЗ.

Рассмотрим примеры задач данного типа:

Корабли находятся в открытом море в точках А и В. Расстояние между точками – 50 км. Корабли одновременно начинают движение друг к другу прямолинейно в независимых направлениях со скоростями соответственно 15 км/ч и 20 км/ч. Найдите наибольшее возможное время движения кораблей до момента их встречи в точке С.

1. По структуре деятельности.

От структуры задачи зависит тип деятельности, необходимой для решения задачи:

• репродуктивная или алгоритмическая деятельность (воспроизведение способа решения);
• продуктивная деятельность (использование известного способа решения в изменившихся условиях, привлечение знаний из других тем);
• эвристическая деятельность (поиск решения творческим путём).

1. По математическому содержанию.

В зависимости от того, какому разделу арифметики компоненты У и З, задачи бывают:

• арифметические,
• алгебраические,
• геометрические,
• тригонометрические и т.д.

1. По методу решения.

В зависимости от того, каким образом представлены компоненты О и Р задачи классифицируют на:

• арифметические, в основе которых лежит зависимость между компонентами арифметических действий.
• алгебраические, задачи, в которых требуется составление уравнений,
• геометрические, задачи, в которых необходимо выполнить построение геометрических фигур, охарактеризовать их свойства,
• комбинированные задачи;

1. По характеру требований.

Классификация задач основана на представлении в задачи компонента З:

• задачи на объяснение,
• задачи на вычисление,
• задачи на доказательство,
• задачи на построение и т.д.

1. По специфике языка:

• текстовые, где условие представлено на естественном языке,
• сюжетные (задачи, в которых присутствует фабула),
• абстрактные – к ним относятся предметные задачи.

Образовательный процесс испытывает на себе влияние со стороны окружающего мира. Так, в информационную эпоху наиболее целесообразным становится образный способ представления информации и комбинация разных способов кодирования. Школьный курс математики преимущество отдается трем способам кодирования:

• словесный,
• символьный,
• образный (таблицы, графики, схемы, чертежи, рисунки).

Образный способ можно разделить на подтипы в зависимости от используемых условных обозначений: образно-графический (требуется чтение и понимание легенды) и образно-иконический (нет необходимости читать легенду). Оба способа предполагают сформированность таких умений, как воспринимать условные обозначения, устанавливать связи между ними и самими объектами.

Следовательно, можно классифицировать задачи с опорой на наличие/отсутствие требования перекодировки информации (т.е. изменить способ представления информации, который использовался в задаче изначально); способ представления задачи одним или несколькими способом кодирования информации.

Таким образом, получим следующую классификацию математических задач по способам кодирования информации:

1. Задачи, не требующие перекодировки.
2. Задачи, требующие перекодировки.

К задачам, не требующим перекодировки (первый тип) можно отнести:

• задачи, представленные с использованием одного способа кодирования (первый тип задач);
• задачи, в которых используется несколько способов кодирования (второй тип задач).

К задачам, требующим перекодировки (третий тип) относятся задачи, в которых требуется изменить способ кодирования, представленный в задаче изначально, а именно:

• задачи на внутриобразные перекодировки;
• задачи на символьно-словесные перекодировки;
• задачи на словесно-образные перекодировки;
• задачи на образно-символьные перекодировки.
• задачи на сложные перекодировки.

Задачи, представленные с использованием преимущественно одного способа кодирования информации (образного, символьного или словесного) требуют решения этим же способом. Следует помнить, что не существует задач, представленных исключительно с использованием образного кодирования: всегда требуется словесный комментарий. При этом решение задачи может быть полностью образным. К тому же, задачи, сформулированные словесно, содержат в себе символы (числа).

Задачи второго типа (задачи, в которых используется несколько способов кодирования) требуют от учащегося умения ориентироваться в разных способах представления информации. Данные задачи не требуют от учащегося перекодировки информации из одного способа в другой, его задача – сориентироваться в данном способе кодирования и представления информации, и найти решение. К задачам такого типа можно отнести задачи на выбор правильного ответа, задачи нас соответствие, при этом условия могут быть представлены разным способом кодирования.

Задачи третьего типа (задачи, требующие перекодировки) в обязательном порядке предполагают перекодировку информации. Решая задачу такого типа, учащийся перекодирует информацию, представляя ее отличным от условия способом. Сложная перекодировка сочетает в себе несколько перекодировок.

Рассмотрим пример задачи второго типа: задачи, в которых используется несколько способов кодирования.

Формы представления информации: словесная и образно-иконическая Данная задача предполагает ее перевод в графическую форму.

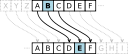
Стадион имеет форму круга с диаметром d. Точка 0 является стартом и финишем. Спортсмен пробегает по окружности стадиона один круг. Изобразите схематически зависимость расстояния между стартом и положением спортсмена (R) от длины пути, который пробежал спортсмен (l).

Рассмотрим пример задачи третьего типа: задача на сложную перекодировку.

Функции 1–6 заданы разными способами. Установите соответствие между функциями (1-6) и промежутками их возрастания (а–д).