Решебник (ГДЗ) по математике 5 класс Виленкин Жохов Чесноков

ГДЗ по Математике 5 класс Виленкин Жохов Чесноков. Учебник Мнемозина ФГОС (ответы к новому и старому учебнику)

Авторы: Н.Я. Виленкин , В.И. Жохов , А.С. Чесноков , С.И. Шварцбурд .

Издательство: Мнемозина

Тип: Учебник

Изучая математику, многие дети не могут обойтись без ГДЗ по математике 5 класс Виленкин. Такая мера полностью оправдана, ведь сам по себе этот предмет очень непростой. К тому же и учителя порой не достаточно четко и ясно разъясняют материал своим подопечным. А большинство родителей слишком заняты, чтобы уделять учебному процессу достаточно внимания. Да многие из них уже и подзабыли все необходимые навыки. Поэтому осваивать такие темы, как:

натуральные числа и шкалы;
арифметические действия с натуральными числами;
площади и объемы;
обыкновенные и десятичные дроби;
инструменты для вычисления и измерения.

Но не все ребята могут это сделать, поэтому помочь им может решебник, где собрана обширная информация по всему текущему курсу. Используя этот сборник, ребята могут добиться значительного прогресса в освоении данной дисциплины. Он будет полезен для всех школьников, от отличников до двоечников.

Когда стоит пользоваться онлайн-помощником по математике за 5 класс Виленкина

В данное пособие вошли две главы, разделенные на восемь параграфов. Авторы приводят разъяснение по сорока четырем темам, которые в них содержаться. Всего в ГДЗ имеется одна тысяча восемьсот сорок девять заданий, на которые даны доскональные ответы. Ученики при помощи их могут проработать каждое решение, найти и исправить любые неточности, повторить ранее пройденный материал.

При этом решебник помогает не только в проверке домашних заданий, но и в подготовке к разноплановым проверочным работам. Благодаря доступно изложенной и подробной информации, школьники могут восполнить недостающие познания.

Лишь немногие ребята с удовольствием ходят на уроки математики. Остальные же просто не понимают этот предмет, поэтому все время дергаются в классе, боясь, что учитель их о чем-то спросит. Больше всего проблем возникает с выполнением д/з, ведь если в школе еще можно что-то спросить, то дома приходится рассчитывать только на себя. Поэтому очень большим подспорьем для учащихся является пособие по математике 5 класс Виленкина, в котором они могут найти много полезной и актуальной информации. Правильно используя этот сборник, можно получать очень хорошие результаты в плане оценок, да и знания в полной мере осядут в памяти.

Глава 1. Натуральные числа

§ 1. Натуральные числа и шкалы

§ 2. Сложение и вычитание натуральных чисел

§ 3. Умножение и деление натуральных чисел

§ 4. Площади и объёмы

Глава 2. Дробные числа

§ 5. Обыкновенные дроби

§ 6. Десятичные дроби. Сложение и вычитание десятичных дробей

§ 7. Умножение и деление десятичных дробей

§ 8. Инструменты для вычисления и измерений

В 5 классе вся школьная программа усложняется, ведь ученики переходят из начальной школы в среднее звено. И, конечно, нельзя не отметить математику, которая приносит больше всего сложностей. Трудно поспорить с тем, что именно ее множество школьников недолюбливает и не понимает, для чего она вообще нужна. Хотя, если задуматься, на ум придет достаточно много простых и житейских примеров: банальная оплата товаров и подсчет процентов со скидки или кредита. Вообще эта дисциплина является языком всех естественных наук, ее формулы и методы нужно для всего: от составления прогнозов погоды и построения новых зданий до глубинного познания космоса. А сколько престижных и высокооплачиваемых профессий связаны с ней! Это и архитектор, и инженер, и строитель, и дизайнер, и многие другие. Конечно, в большинстве своем он только технические, но это не значит, что не интересные, так как и в них есть место творчеству и самовыражению. К тому же, этот предмет способствует развитию логического мышления, тренирует память, формирует вычислительные способности и вообще очень тренирует мозг.

Для того чтобы дети действительно вдумчиво изучали этот предмет, необходимо создать им комфортные условия. То есть, чтобы дома они могли заниматься самостоятельно в удобное для них время, тогда домашняя работа не будет таким испытанием ни для детей, ни для их родителей. Поможет в самообучении решебник, составленный командой опытных методистов и выпущенный издательством «Мнемозина».

Как именно ГДЗ по математике за 5 класс (авторы: Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд) сможет помочь школьникам

Предложенный справочник будет верным другом для вашего ребенка, так как решение каждой задачки объяснено максимально понятно и доходчиво. Ученик не будет просто сидеть и бездумно списывать, ведь детальное пояснение и комментарии авторов помогут ему по-настоящему вникнуть в материал. Так же мамы и папы смогут с помощью задачника проверять д/з и не тратить на это слишком много времени после работы. Другие достоинства:

наличие правильных ответов ко всем заданиям;
простая и быстрая навигация по сайту;
соответствие рабочим программам;
сайт поддерживает все мобильные электронные устройства с доступом в интернет;
онлайн-режим.

Содержание учебно-методического комплекса по математике для 5 класса от Виленкина

Данная книга содержит все главы, параграфы и разделы, которые рекомендованы к изучению в конкретный период обучения:

обозначение натуральных чисел (шкалы и координаты);
числовые, буквенные выражения;
степень, квадрат, куб числа;
доли. Обыкновенные дроби;
приближенные значения, округление;
инструменты для вычислений и измерений.

Математика 5 класс. Виленкин

901
902
903
904
905
906
907
908
909
910
911
912
913
914
915
916
917
918
919
920
921
922
923
924
925
926
927
928
929
930
931
932
933
934
935
936
937
938
939
940
941
942
943
944
945
946
947
948
949
950
951
952
953
954
955
956
957
958
959
960
961
962
963
964
965
966
967
968
969
970
971
972
973
974
975
976
977
978
979
980
981
982
983
984
985
986
987
988
989
990
991
992
993
994
995
996
997
998
999
1000

1101
1102
1103
1104
1105
1106
1107
1108
1109
1110
1111
1112
1113
1114
1115
1116
1117
1118
1119
1120
1121
1122
1123
1124
1125
1126
1127
1128
1129
1130
1131
1132
1133
1134
1135
1136
1137
1138
1139
1140
1141
1142
1143
1144
1145
1146
1147
1148
1149
1150
1151
1152
1153
1154
1155
1156
1157
1158
1159
1160
1161
1162
1163
1164
1165
1166
1167
1168
1169
1170
1171
1172
1173
1174
1175
1176
1177
1178
1179
1180
1181
1182
1183
1184
1185
1186
1187
1188
1189
1190
1191
1192
1193
1194
1195
1196
1197
1198
1199
1200

1301
1302
1303
1304
1305
1306
1307
1308
1309
1310
1311
1312
1313
1314
1315
1316
1317
1318
1319
1320
1321
1322
1323
1324
1325
1326
1327
1328
1329
1330
1331
1332
1333
1334
1335
1336
1337
1338
1339
1340
1341
1342
1343
1344
1345
1346
1347
1348
1349
1350
1351
1352
1353
1354
1355
1356
1357
1358
1359
1360
1361
1362
1363
1364
1365
1366
1367
1368
1369
1370
1371
1372
1373
1374
1375
1376
1377
1378
1379
1380
1381
1382
1383
1384
1385
1386
1387
1388
1389
1390
1391
1392
1393
1394
1395
1396
1397
1398
1399
1400

1501
1502
1503
1504
1505
1506
1507
1508
1509
1510
1511
1512
1513
1514
1515
1516
1517
1518
1519
1520
1521
1522
1523
1524
1525
1526
1527
1528
1529
1530
1531
1532
1533
1534
1535
1536
1537
1538
1539
1540
1541
1542
1543
1544
1545
1546
1547
1548
1549
1550
1551
1552
1553
1554
1555
1556
1557
1558
1559
1560
1561
1562
1563
1564
1565
1566
1567
1568
1569
1570
1571
1572
1573
1574
1575
1576
1577
1578
1579
1580
1581
1582
1583
1584
1585
1586
1587
1588
1589
1590
1591
1592
1593
1594
1595
1596
1597
1598
1599
1600

1701
1702
1703
1704
1705
1706
1707
1708
1709
1710
1711
1712
1713
1714
1715
1716
1717
1718
1719
1720
1721
1722
1723
1724
1725
1726
1727
1728
1729
1730
1731
1732
1733
1734
1735
1736
1737
1738
1739
1740
1741
1742
1743
1744
1745
1746
1747
1748
1749
1750
1751
1752
1753
1754
1755
1756
1757
1758
1759
1760
1761
1762
1763
1764
1765
1766
1767
1768
1769
1770
1771
1772
1773
1774
1775
1776
1777
1778
1779
1780
1781
1782
1783
1784
1785
1786
1787
1788
1789
1790
1791
1792
1793
1794
1795
1796
1797
1798
1799
1800

У нас вы можете найти готовые домашние задания по математике для учеников 5 класса, которые изучают предмет по книге «Математика 5 класс. Учебник для общеобразовательных учреждений», написанной Виленкиным Н.Я., Жоховым В.И., Чесноковым А.С. и Шварцбургом С.И. Во всех 1849 решениях задачах приведено полное описание и вариант краткой записи. В полное описание включены этапы решения и правила, на которых оно основано, в кратком варианте приведено условие и решение без пояснений.

ГДЗ по математике 5 класса Виленкина включают не только печатные варианты решения задачи, но и рукописные. Преимуществом последних является последовательность решения, наличие схем и способы решения задачи. Это позволяет на понятном и простом примере объяснить ребенку 11-12 лет план и варианты решения. Процент усвоения в таком случае намного выше, чем при самостоятельном изучении темы и решении заданий по ней.

В пятом классе обычно не только дети сталкиваются с трудностями при решении домашнего задания, но и родители. Причиной тому является контроль и проверка правильности подготовки уроков к следующему учебному дню. Одним из непростых уроков является математика, она тяжела для восприятия и требует тщательной проработки всех тем. Родители могут не помнить, как решаются подобные задачи, в таком случае им на помощь приходит «решебник».

Для решения задач из учебника за 5 класс Виленкина необходимо вспомнить правила, которые были объяснены на уроке. Для удобства они приводятся перед решением задачи. Это позволяет родителям не пользоваться учебником и сократить количество материала для детей. После правил приводится схема решения, которая обеспечивает простоту понимания и создает структуру решения. При этом соблюдается правило увеличения сложности, постепенно появляются все более сложные примеры. Для запоминания правил приводится большое количество однотипных заданий, на основании которых ученики вырабатывают определенный алгоритм решения.

Ответы на задачи предназначены для повышения уровня знаний, усвоения темы за счет решения более сложных задач, а также проверки правильности результата. Кроме того, они рассчитаны на закрепление порядка решения, что позволит без труда определять ответы в будущем.

В большинстве российских школ пользуются именно учебником Виленкина. Мы стараемся научить понимать математику, т.к. она на самом деле является интересной наукой. Пользуясь развитой логикой, способностью структурировано мыслить и сообразительностью можно решить любую задачу. Поиск ответа на задачи повышенной сложности с изучением новых приемов и схем работы расширит кругозор и заинтересует ребенка.

Задания по математике 5 класс: для занятий дома

Самостоятельные занятия с ребенком в домашних условиях играют важную роль в процессе обучения. Даже не имея специального образования можно самостоятельно прорешивать с ним примеры и задачи по основным темам, встречающимся в текущем учебном году.

Эти задания вы можете распечатать на принтере.

§ Как правильно заниматься дома

Для того чтобы занятия действительно приносили пользу, необходимо придерживаться определенных правил, которые помогут сделать день продуктивнее, без утомления ребенка:

Самое главное правило, которое пригодиться не только школьнику, но и любому взрослому человеку, это правильное чередования умственного труда и физического. Необходимо составить распорядок дня так, чтобы после физических нагрузок обязательно шли более спокойные, умственные занятия. Нельзя делать уроки сразу же после возвращения из школы, то же самое касается и дополнительных занятий.
Для решения задач вне школьной программы лучше всего выбирать менее загруженные уроками дни.
Во время занятий нужно убрать все отвлекающие факторы, для того чтобы внимание ребенка не рассеивалось. Если есть возможность решить важные дела перед уроками, то лучше сделать это заранее.
Начинать всегда нужно со сложных задач, а затем переходить к более простым.
Обязательно нужно хвалить ребенка за его достижения и правильно выполненную работу.
Для того чтобы мозг работал, детям нужно давать шанс самостоятельно решать примеры и задачи. Даже если в течение долгого времени он не может найти ответ, не нужно делать очевидных подсказок, пусть он найдет путь решения самостоятельно.
Хорошо запоминать принцип математических решений помогают ассоциации, например, дроби можно представлять как кусочки одного торта или яблока.

§ Задания для 5 класса на тему «Натуральные числа»

Перед тем как познакомиться с обыкновенными и десятичными дробями, необходимо вспомнить что такое натуральные числа. Ими называются числа, используемые в повседневной жизни, например для счета предметов.

✍ 3адание 1

Определить, какое число стоит перед:

65;
756;
3 857;
45 940.

Определить, какое число на две единицы больше, чем:

404;
543;
6 348;
2 450.

✍ 3адание 2

Написать в виде словосочетаний следующие цифры:

547;
3 417;
814 261;
57 309.

✍ 3адание 3

Представить в виде чисел словосочетания:

триста шестьдесят девять;
одна тысяча двести девяносто три;
десять тысяч шестьсот восемьдесят восемь;
двести пятнадцать тысяч семьсот двадцать четыре.

§ 3адания на тему «Сравнения натуральных чисел»

При помощи сравнения можно определить какое из чисел меньшее, а какое большее. Те что меньше, стоят при счете раньше, чем те, что больше.

✍ 3адание

Расставить 3наки « » или «=» между числами:

18 32;
54 16;
347 524;
546 546;
675 23 433;
563 736 634;
392 450 81;
5 453 5 543;
949 3 432 563;
101 101 3 455 456.

§ 3адания на тему «Сложение, вычитания натуральных чисел»

✍ 3адание 1

Для того чтобы повторить сложение, вычитание чисел, а также порядок действий при вычислении сложного выражения, можно решить несколько выражений:

24 • (58 + 114) — 336;
(563 — 260 : 4) + 61 • 37;
7 354 — (354 + 193 • 4) + (743 — 25);
(1 623 + 570 : 30) — (3 540 — 413 • 7).

Ответ: 1) 3 792, 2) 2 755, 3) 6 946, 4) 993.

✍ 3аданиие 2

В саду росло 208 фруктовых деревьев. Яблонь и слив было 129 штук, а слив и груш — 115. Сколько яблонь росло в саду? Слив? Груш?

Решение: Если известно, что всего деревьев было 208, а яблонь и слив – 129, то можно вычислить количество груш.

1 действие: 208 – 129 = 79 грушевых деревьев.
Стало известно количество грушевых деревьев, значит можно узнать, сколько было слив.
2 действие: 115 – 79 = 36 сливовых деревьев.
После того, как стало известно, сколько было груш и слив, можно высчитать количество яблонь.
3 действие: 208 – (79 + 36) = 93 яблонь.

Ответ: В саду росло 93 яблони, 79 груш и 36 слив.

§ 3адания на тему «Луч, прямая, отрезок»

Отрезком называется часть прямой ограниченная двумя точками, его длинной считается расстояние между крайними точками. Луч — это часть прямой, которая состоит из точки и всех других точек, лежащих по одну сторону от нее.

✍ 3адание 1

Начертите отрезок АВ, равный 12 см. Отметьте на нем точки по порядку С и D так, чтобы отрезок АС был равен 4 см, а СD — 6 см. Вычислите, чему равен отрезок DВ?

Ответ: 12 — (4 + 6) = 2 см.

✍ 3адание 2

Начертите произвольную прямую и отметьте на ней два точки А, В и С так, чтобы длина отрезка АВ была 7 см, а отрезка ВС — 4 см. Какова длина отрезка АС?

Ответ: 7 + 4 = 11 см.

§ 3адания на тему «Уравнения»

Уравнением называется равенство, в котором один или несколько компонентов являются неизвестными.

✍ 3адание 1

Решить уравнения

84 • x = 588;
4 • (18 + x) = 96;
14x — 8x = 18;
50 + 6x — 31 = 4;
13х + 20 — 4х — 16 + х = 54.

Ответ: 1) x=7, 2) х=6, 3) х=3, 4) х=-2,5, 5) х=5.

✍ 3адание 2

Насте 12 лет, что на 4 года меньше, чем возраста Лены. Сколько лет Лене? Решить уравнением.

Решение: Возьмем возраст Лены за x, в таком случае можно составить уравнение:
x – 4 = 12,
х = 12 + 4 = 16.

Ответ: Лене 16 лет.

✍ 3адание 3

Велосипедист за 3 дня проехал 117 км. Какое расстояние он преодолел в первый день, если в последующие два дня он проезжал на 4 км больше, чем в предыдущий? Какое расстояние он преодолел во 2-й и 3-й дни?

Решение: Расстояние которое проехал велосипедист за 1-й день, возьмем за x. В таком случае, второй день будет выглядеть как: x + 4, а третий: (х + 4) + 4.

Можно составить уравнение:

_{1 день 2 день 3 день}

х + (х + 4) +( х + 4 + 4) = 117
3х + 12 = 117
3х = 117 – 12 = 105
х = 105: 3 = 35.

Проверка: 35 + 35 + 4 + 35 +4 + 4 = 117

Ответ: В первый день велосипедист проехал 35 км. Во 2-й день: 35 + 4 = 39 км. В 3-й день: 35 + 4 + 4 = 43 км.

§ 3адания на тему «Квадрат и куб числа»

Квадратом числа называется произведение этого числа самого на себя. Куб — произведение числа самого на себя два раза.

✍ 3адание 1

Найти квадрат чисел:

5;
9;
13;
45;
100;
381.

Ответ: 1) 25, 2) 81, 3) 169, 4) 2025, 5) 10 000, 6) 145 161.

Найти куб чисел:

2;
6;
11;
36;
78;
115.

Ответ: 1) 8, 2) 216, 3) 1 331, 4) 46 656, 5) 474 552, 6) 1 520 875.

✍ 3адание 2

Решить выражения:

(7 + 4) 2 • 6;
5 352 — (47 2 + 4 3 );
61 2 — 7 • 2 3 + (20 — 4) 2 ;
( 5 + 26 ) 2 — ( 6 + 12 ) 2 — 69;
(25 — 16) 3 + (36 — 33) 2 ;
( 5 + 6 ) 3 — ( 5 + 24) 2 + 727.

Ответ: 1) 726, 2) 3 079, 3) 3 921, 4) 568, 5) 738, 6) 1 217.

§ 3адания на тему «Обыкновенные дроби»

✍ 3адание 1

1. Паша собрал 34 гриба, из которых 16 грибов оказались подосиновиками. Какую часть от всех грибов составляют подосиновики?

Ответ: 8/17.

2. Всего в книге 124 страниц, из которых Толя прочитал ровно половину. Какую часть книги прочитал Толя?

Ответ: 1/2.

3. Оля собрала всего 38 ягод, из которых 17 штук были малиной. Какую часть от общего количества составляют остальные ягоды?

✍ 3адание 2

Начертите отрезок и разделите его на 13 равных частей. Отметьте на данном отрезке: 3/13, 6/13, 10/13.

✍ 3адание 3

1. Полина собрала 36 листьев, из которых березовые составляют 6/18. Сколько березовых листьев собрала Полина?

Ответ: 12.

2. Папа был на рыбалке и поймал всего 45 рыбок, 8/15 было карасей. Сколько карасей поймал папа?

Ответ: 24.

3. Мама стряпала пирожки, всего их получилось 32 штуки. 5/8 от общего количества были с капустой. Сколько пирожков с капустой состряпала мама?

Ответ: 20.

✍ 3адание 4

Сравнить дроби:

3/4 и 5/6;
12/13 и 7/26;
21/30 и 5/10;
7/20 и 8/12.

§ 3адания на тему «Сложение и вычитание обыкновенных дробей»

✍ 3адание 1

7⁄30 + 18⁄30 — 6⁄30;
3⁄19 + 8⁄19 — 4⁄19;
19⁄25 — ( 21⁄50 + 2⁄25 ) — 6⁄25;
13⁄76 — 11⁄76 + 49⁄76;
27⁄129 + ( 12⁄86 — 6⁄43 ) — 7⁄43.

Ответ: 1) 19/30, 2) 7/19, 3) 1/50, 4) 51/76, 5) 2/43.

✍ 3адание 2

Расстояние от дома до школы составляет 4/11 км, а от школы до магазина — 5/11 км. Чему равно расстояние от дома до магазина?

Решение: Для того чтобы найти сколько составляет весь путь, необходимо сложить расстояние от дома до школы и расстояние от школы до магазина 4/11 + 5/11 = 9/11 (км).

Ответ: Расстояние от дома до магазина составляет 9/11 км.

✍ 3адание 3

От рулона ткани первый раз отрезали 7/15 части, а затем еще 5/15, после чего в рулоне осталось 27 м. Сколько метров длина рулона?

Решение: В первую очередь нужно узнать какая часть рулона осталась.

1 действие: 15/15 — 7/15 — 5/15 = 3/15.

Можно сделать вывод, что 27 м составляет 3/15 части от всего рулона. Для того чтобы найти длину всего рулона ткани, необходимо узнать, сколько метров составляет 7/15 и 5/15 частей.

2 действие: 27 : 3 = 9 (м) — в 1 части.

3 действие: 9 • 7 = 63 (м) — составляет 7/15.

4 действие: 9 • 5 = 45 (м) — составляет 5/15.

После того, как стало известно какая длина у каждой из частей, можно вычислить всю длину рулона.

5 действие: 63 + 45 + 27 = 135 (м).

Ответ: длина рулона 135 метров.

§ 3адания на тему «Умножение и деление обыкновенных дробей»

✍ 3адание 1

8/13 • 1/2;
4/24 : 6/12;
3/21 • 7/9 : 2/4;
18/20 • 5/8 : 6/14;
2/5 : 15/30 • 9/11.

Ответ: 1) 4/13, 2) 1/3, 3) 2/9, 4) 21/16, 5) 36/55.

✍ 3адание 2

В первом ящике лежит 3/16 от всего количества яблок, а во втором в 3 раза больше. Какая часть от всего количества яблок лежит в обоих ящиках?

Решение: Сначала нужно узнать сколько яблок лежит во втором ящике.

1 действие: 3/16 •3 = 9/16 (яб.).

После того как стало известно сколько яблок лежит во втором ящике, можно узнать их общее количество.

2 действие: 3/16 + 9/16 = 12/16 = 3/4 (яб.)

Ответ: 3/4 части от общего количества яблок лежит в обоих ящиках.

✍ 3адание 3

3а два дня автомобиль поехал 6/10 пути. Известно, что во второй день он проделал путь в 4 раза больше, чем в первый. Cколько проехал автомобиль в первый и второй день?

Решение: Пусть первый день пути будет x, тогда можно составить уравнение x + х • 4 = 6/10.

х + х • 4 = 6/10;
5 • x = 6/10;
х = 6/10 : 5;
х = 3/25 — проехал автомобиль в 1 день.

После того как стало известно, какая часть пути была преодолена в 1 день, можно высчитать 2 день.

2 действие: 3/25 • 4 = 12/25.

Ответ: в первый день автомобиль проехал 3/25, а во второй — 12/25.

§ 3адания на тему «Десятичные дроби»

✍ 3адание 1

Представить обыкновенные дроби в виде десятичных:

5/10;
13/100;
5/25;
164/1000;
45/250.

Ответ: 1) 0,5; 2) 0,13; 3) 0,2; 4) 0,164; 5) 0,18.

✍ 3адание 2

Начертите отрезок, разделите его на 6 равных частей. Отметьте на нем точки 0,3; 1,5; 2,2; 3,7; 4; 5,6.

§ 3адания на тему «Сложение и вычитание десятичных дробей»

✍ 3адание 1

28,3 + 4,45;
58,9 + 18,1;
0,48 + 6,8;
34,1 — 2,2;
39 — 20,3;
15,28 — 6,347.

Ответ: 1) 32,75; 2) 77; 3) 7,28; 4) 31,9; 5) 18,7; 6) 8,933.

✍ 3адание 2

В первый день катер проплыл 3,5 км, во второй на 4,31 км больше, а в третий — на 0,9 км меньше, чем во второй. Сколько всего км проплыл катер за 3 дня?

Решение: Необходимо вычислить, сколько катер проплыл в первый и во второй день.

1 действие: 3,5 + 4,31 = 7,81 (км) — проплыл во второй день.

2 действие: 7,81 — 0,9 = 6,91 (км) — проплыл в третий день.

После того как стало известно, сколько было пройдено за каждый день, можно узнать весь путь.

3 действие: 3,5 + 7,81 + 6,91 = 18,22 (км).

Ответ: за три дня катер проплыл 18,22 км.

§ 3адания на тему «Умножение и деление десятичных дробей»

✍ 3адание 1

5,6 • 8,34;
11,4 • 24,08;
0,56 • 34,9;
6,8 : 3,2;
33,021 : 12,23;
59,72 : 6,26.

Ответ: 1) 46,704; 2) 274,512; 3) 19,544; 4) 2,125; 5) 2,7; 6) 9,54.

✍ 3адание 2

3агадано число, если его увеличить в 3 раза, а затем прибавить 2,16, то получиться 27,96. Какое число было загадано?

Решение: Пусть неизвестное число будет x, тогда можно составить уравнение х • 3 + 2,16 = 27,96.

х • 3 + 2,16 = 27,96;

Ответ: было загадано число 8,6.

✍ 3адание 3

Расстояние между населенными пунктами равно 53,7 км. Навстречу друг другу вышли два пешехода, скорость первого 3,8 км/ч, второго — 4,6 км/ч. Какое расстояние будет между ними через 2,7 часа?

Решение: Нужно вычислить, какое расстояние пешеходы пройдут за 2,7 часа.

1 действие: 3,8 • 2,7 = 10,26 (км) — пройдет первый пешеход.

2 действие: 4,6 • 2,7 = 12,42 (км) — пройдет второй пешеход.

После того как стало известно, сколько прошли пешеходы, можно высчитать, какой путь им еще нужно преодолеть до встречи друг с другом.

3 действие: 53,5 — 10,26 — 12,42 = 30,82 (км).

Ответ: через 2,7 часа между пешеходами будет 30,82 км.

Виленкин Н.Я.. Книги онлайн

Наум Яковлевич Виленкин (30 октября 1920, Москва — 19 октября 1991) — советский математик, популяризатор математики. Автор известных школьных учебников по математике для 5 и 6 классов, которые служат уже более сорока лет. Первые учебники были изданы в сентябре 1970 года (в соавторстве с К. И. Нешковым, С. И. Шварцбурдом, А. Д. Семушиным, А. С. Чесноковым, Т. Ф. Нечаевой).

Учился в «7-й опытной школе имени проф. Коваленского» в Кривоарбатском переулке. Затем окончил МГУ (1942); доктор физико-математических наук (1950), профессор (1951). С 1943 года работал в различных вузах, с 1961 года — в Московском заочном педагогическом институте.

Первые работы, в том числе диссертация, были посвящены теории топологических групп. Развивая теорию характеров Понтрягина, установил связь между системами характеров нульмерных компактных абелевых групп, известных также как системы Виленкина, с классом ортонормированных систем кусочно постоянных функций.

Начиная с 1950-х годов введённые Виленкиным системы активно изучаются в связи с широким применением в области цифровой обработки сигналов.

С середины 1950-х работал над изучением теории представлений групп Ли, где получил ряд результатов, связанных с бесконечномерными представлениями, построенными И. М. Гельфандом и М. А. Наймарком.

Является автором монографии «Специальные функции и теория представлений групп» (1965, 1991), которая затем была (совместно с А. У. Климыком) преобразована в «Representations of Lie groups and special functions» (1991–1993, 1995).

Автор научно-популярных книг «Рассказы о множествах», «Комбинаторика», ряда школьных учебников по математике.

Книги (16)

Соавтор: Ивашев-Мусатов О.С., Шварцбурд С.И.

Учебник соответствует требованиям Федерального государственного стандарта среднего образования, предназначен для изучения курса алгебры и начал математического анализа в 10-м классе на углубленном уровне.

В учебнике выделены типовые задачи для подготовки учащихся к единому государственному экзамену, предложены алгоритмы их выполнения и варианты заданий для самоконтроля, реализованы современные подходы к формированию проектно-исследовательских умений и ИКТ-компетенций. Темы индивидуальных проектов, предложенные в учебнике, входят в базовое академическое образование по экономике.

Соавтор: Ивашев-Мусатов О.С., Шварцбурд С.И.

Учебник соответствует требованиям ФГОС среднего общего образования. В книге выделены типовые задачи для подготовки учащихся к Единому государственному экзамену, предложены алгоритмы их выполнения и варианты заданий для самоконтроля.

В учебнике реализованы современные подходы к формированию проектно-исследовательских умений и ИКТ-компетенций. Темы индивидуальных проектов, предложенные в учебнике, входят в базовое академическое образование по экономике.

Наряду с теоретическим материалом пособие содержит большое количество подробно разобранных примеров, а также упражнения для самостоятельного решения.

Соавтор: Сурвилло Г.С., Симонов А.С., Кудрявцев А.И

Издание для учащихся 9 класса с углубленным изучением математики.

Особенность этого издания — систематическая демонстрация возможностей курса математики 9 класса при решении важных задач современной экономики.

За последнее столетие одно из центральных мест в математической науке завяла созданная немецким математиком Г.Кантором теория бесконечных множеств, понятия которой отражают наиболее общие свойства математических объектов. Однако в этой теории был вскрыт ряд парадоксов, вызвавших у многих видных ученых сомнения в справедливости ее основ.

В данной книге излагается в популярной форме, какими путями шла человеческая мысль в попытках понять идею бесконечности как в физике, так и в математике, рассказывается об основных понятиях теории множеств, истории развития этой науки, вкладе в нее русских ученых.

Книга адресована учащимся старших классов, желающим расширить и углубить знания по всем разделам математики. Изложение новых математических понятий опирается на школьный курс и сопровождается интересными историческими фактами.

Книга погружает учащихся в мир современной математики, рассказывает о роли ученых — математиков в развитии мировой науки. Теоретические сведения дополнены разнообразными задачами.

Книга поможет школьникам расширить знания по математике, повысить математическую культуру. Материал излагается в доступной и занимательной форме с привлечением исторических фактов.

Книга предназначена для внеклассного чтения.

В книге о комбинаторных проблемах рассказывается в занимательной, популярной форме. Тем не менее в ней разбираются и некоторые довольно сложные комбинаторные задачи, дается понятие о методах рекуррентных соотношений и производящих функций.

Соавтор: Пышкало А.М., Рождественская В.В, Стойлова Л.П.

Книга предназначена будущим учителям начальных классов. Она соответствует как программе для педагогических институтов, так и содержанию действующих учебников математики для I-III классов.

Соавтор: Жохов В.И., Чесноков А.С., Шварцбурд С.И.

Основа хорошего понимания математики — умение считать, думать, рассуждать, находить удачные решения задач. Все эти навыки и способности вы можете выработать, если будете настойчивы, трудолюбивы и внимательны на уроках, будете самостоятельно и с интересом заниматься дома.

Соавтор: Куницына Е.С., Мордкович А.Г.

Учебно-методическое пособие для студентов-заочников физико-математических факультетов пединститутов, которое содержит изложение курса дифференциального исчисления (производная) и его приложений к исследованию функции.

Комбинаторика — важный раздел математики, знание которого необходимо представителям самых разных специальностей. С комбинаторными задачами приходится иметь дело физикам, химикам, биологам, лингвистам, специалистам по кодам и др. Комбинаторные методы лежат в основе решения многих задач теории вероятностей и ее приложений.

В книге в популярней форме рассказывается об интересных комбинаторных задачах и методах их решения.

В 70-х годах XIX века немецкий математик Г. Кантор создал новую область математики — теорию бесконечных множеств. Через несколько десятилетий почти вся математика была перестроена на теоретико-множественкой основе. Понятия теории множеств отражают наиболее общие свойства математических объектов.

Обычно теорию множеств излагают в учебниках для университетов и пединститутов. В настоящей книге в популярной форме излагаются основные понятия а результаты теории множеств. Значительную часть книги составляет рассказ известного героя польского писателя С. Лема звездопроходца Иона Тихого о необыкновенной космической гостинице, где было бесконечно много номеров.

Решение многих задач элементарной алгебры значительно облегчается, если использовать симметричность условия задачи.

В этой книге рассказывается, как использовать симметрию при решении систем уравнений, иррациональных уравнений, неравенств ит. д. Все эти задачи решаются единообразным методом, основанным на теории симметрических многочленов.

Книга будет полезна школьникам, готовящимся к конкурсным экзаменам, студентам пединститутов и учителям математики.

Решение очень многих важных задач математической физики и техники не может быть выражено с помощью обычных, элементарных функций, и тогда приходят на помощь специальные функции (функции Лежандра, функции Бесселя, гипергеометрическая функция и т. д.). Теория специальных функций очень детально разработана и включает в себя необозримое множество формул и соотношений, выводимых самыми разнообразными методами, что затрудняет ее изучение.

Целью данной книги является изложение теории специальных функций с единой точки зрения при помощи теории представлений групп. Этот подход позволяет единым образом получать всевозможные соотношения между специальными функциями, как ранее известные, так и новые.

В книге рассказывается о различных приложениях элементарных функций, изучаемых в школе, о развитии и применениях дифференциального и интегрального исчислений, о том, как математики ищут оптимальные решения задач.

Математика 1 класс учебник Моро 1, 2 часть

Часть 1. Страницы

Часть 2. Страницы

Дополнительное ГДЗ Моро

Рабочая тетрадь по математике 1 класс Моро, Волкова
Проверочные работы по математике 1 класс Волкова

Описание

Сборник готовых домашних заданий по учебнику М.И. Моро, С.И. Волковой, С. В. Степановой «Математика 1 класс» демонстрирует принципы выполнения основных номеров.

Для удобства материал разбит на две части. Страницы ГДЗ строго соответствуют учебнику. Имеются необходимые пояснения к аналитическим заданиям, краткие записи задач на сложение, вычитание, чертежи, неравенства.

Преимущество пособия состоит в том, что оно представляет решения упражнений под чертой, что не всегда встречается у авторов других ГДЗ.

Высококачественные иллюстрации выглядят чётко, разборчиво. Наглядное объяснение алгоритмов помогает понять принципы решения, поэтапной записи, итогового оформления. Это позволяет оперативно передавать навыки работы детям.

Математика 6 Виленкин. Задачи 381-431

Упражнения №№ 381-431 по математике в 6 классе из учебника УМК Виленкин с ответами. § 2. Сложение и вычитание дробей с разными знаменателями. 12. Сложение и вычитание смешанных чисел. Математика 6 Виленкин. Задачи 381-431. Цитаты из учебника использованы в учебных целях. Ответы адресованы родителям.

Математика 6 класс Виленкин
12. Упражнения 381-431.

№ 381. Выполните сложение: а) 3 2 /₇ + 5 3 /₁₄; б) 5 7 /₈ + 2 5 /₁₂; в) 7 3 /₈ + 1 5 /₆; …

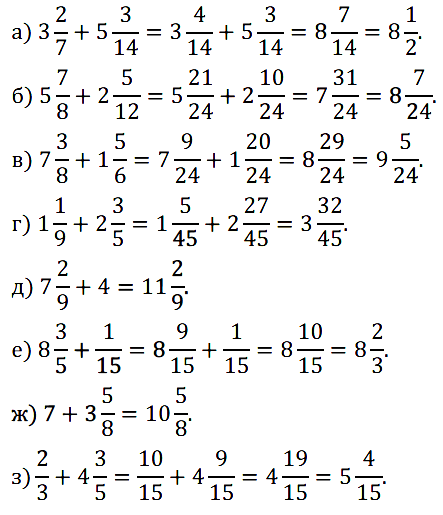
№ 382. Выполните вычитание: а) 1 – 3/4; б) 2 – 5/6; в) 9 – 11/12; г) 7 – 1 7 /₈; …

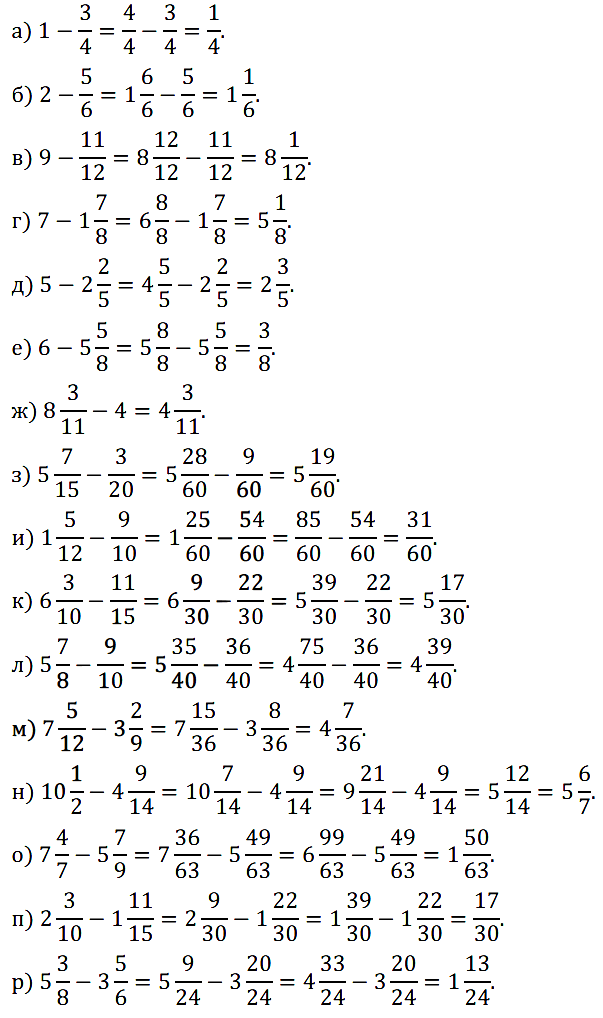
№ 383. Найдите значение выражения: а) 1/4 – (1 – 11/12); б) 2 – (13/33 – 5/22); …

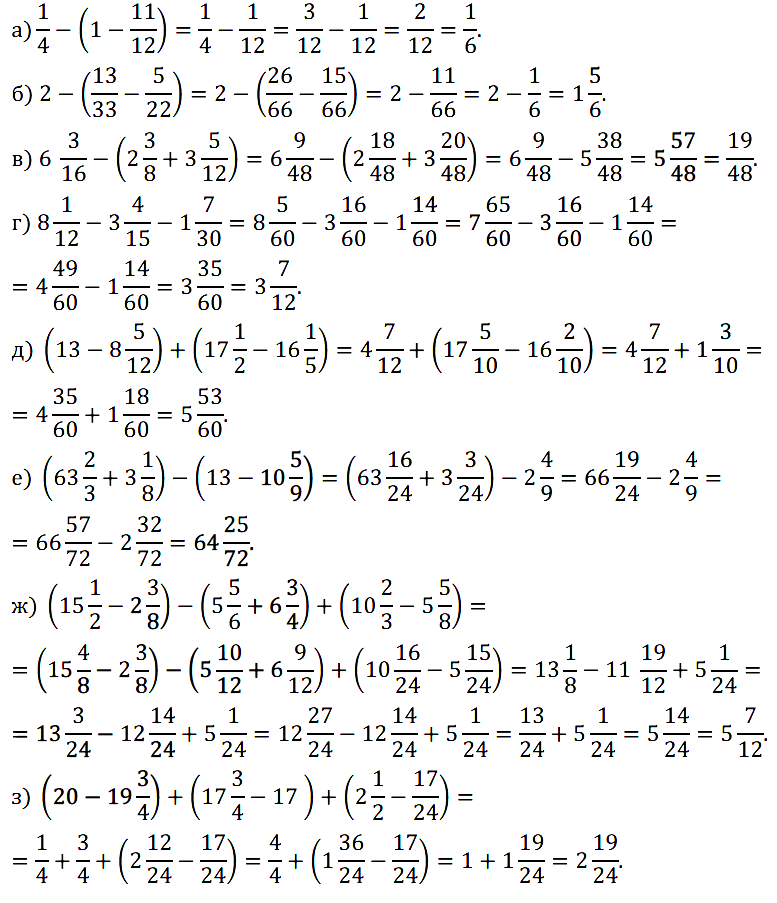
№ 384. Выполните действие: а) 2,4 + 1 2 /₃; б) 3,7 – 2 2 /₅; в) 4 1 /₆ – 6,2; г) 9 4 /₁₅ – 1,8.

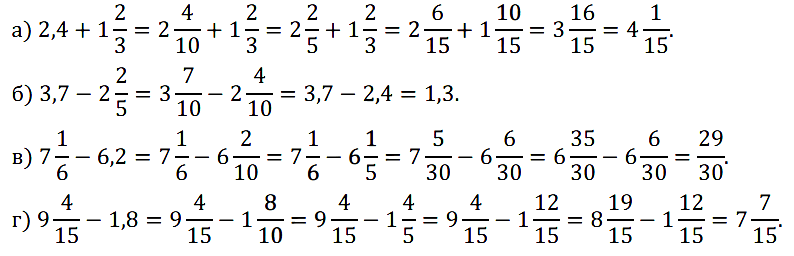
№ 385. Решите уравнение: а) х + 2 2 /₁₁ = 5; б) 26 5 /₈ + а = 30; …

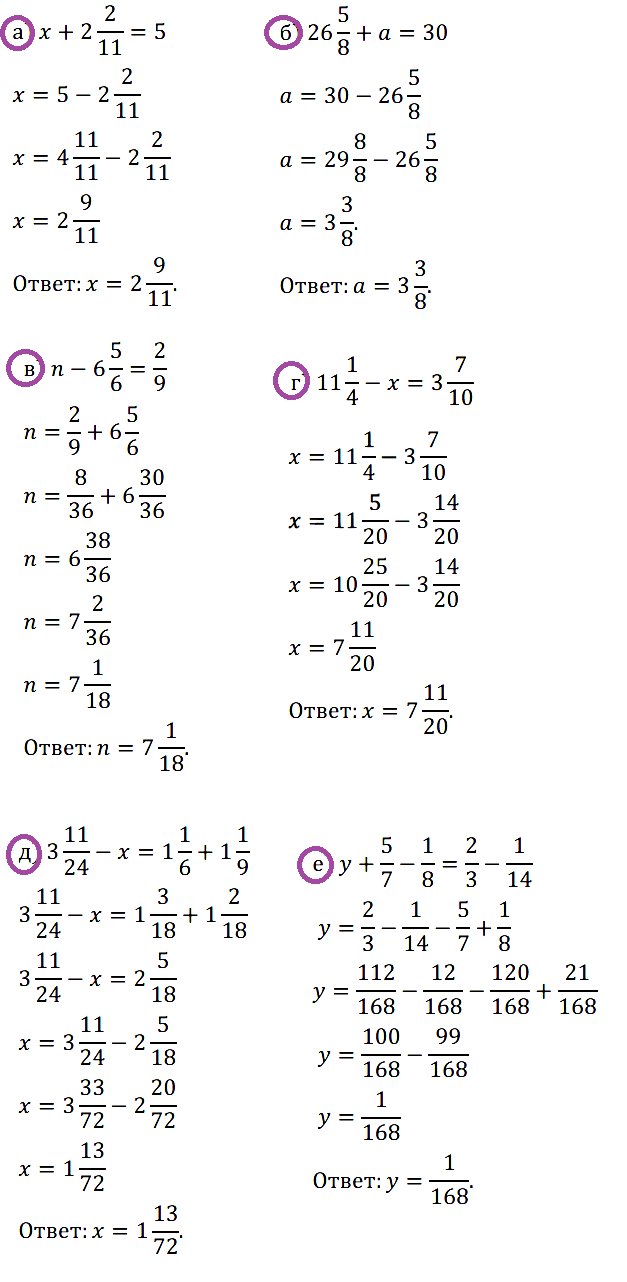
№ 386. Найдите по формуле А = m – 6 1 /₂:
а) значение А, если m = 6 3 /₄; 8 7 /₈; 11; б) значение m, если А = 6 3 /₄; 3 5 /₈; 0.

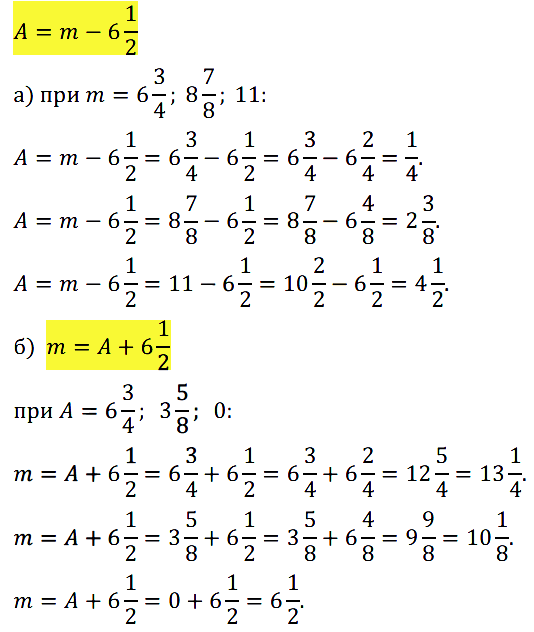
№ 387. Школьный бассейн наполняется через первую трубу за 4 ч, а через вторую — за 6 ч. Какую часть бассейна останется наполнить после совместной работы обеих труб в течение часа?

№ 388. Новая машина может выкопать канаву за 8 ч, а старая — за 12 ч. Новая машина работала 3 ч, а старая 5 ч. Какую часть канавы осталось выкопать?

№ 389. От ленты длиной 8 м отрезали кусок длиной 3 7 /₂₅ м. Найдите длину оставшейся части.

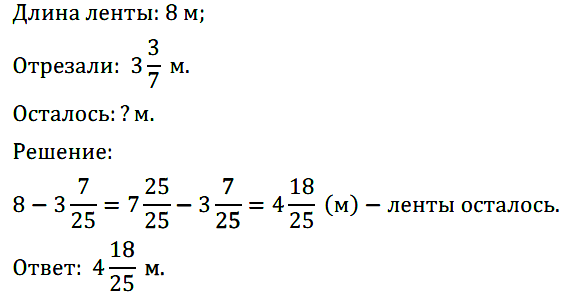
№ 390. Одна шахматная партия длилась 11/12 ч, а другая — 5/6 ч. Сколько времени длилась третья партия, если на все три партии было затрачено 3 ч?

№ 391. Когда от верёвки отрезали кусок, то оставшаяся часть имела длину 2 м. Какой длины была бы оставшаяся часть, если бы от верёвки отрезали на 2/5 м меньше? на 3/4 м больше?

№ 392. Запишите все числа, знаменатель дробной части которых равен 12, большие 2 1 /₃ и меньшие 3 1 /₁₂.

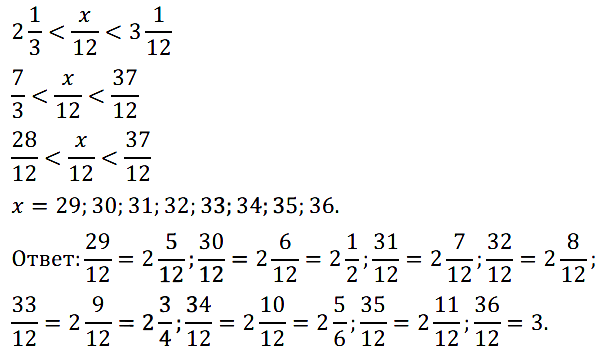
№ 393. На координатном луче отмечена точка А (m/n) (рис. 17). Отметьте на луче точки, координаты которых равны:
a) 1 + m/n; б) 2 – m/n; в) 2 + m/n; г) 1 + 1 m /_n.

№ 394. Найдите периметр треугольника АВС, если АВ = 3 2 /₅ м, ВС = 2 3 /₄ м и АС = 2 7 /₁₀ м.

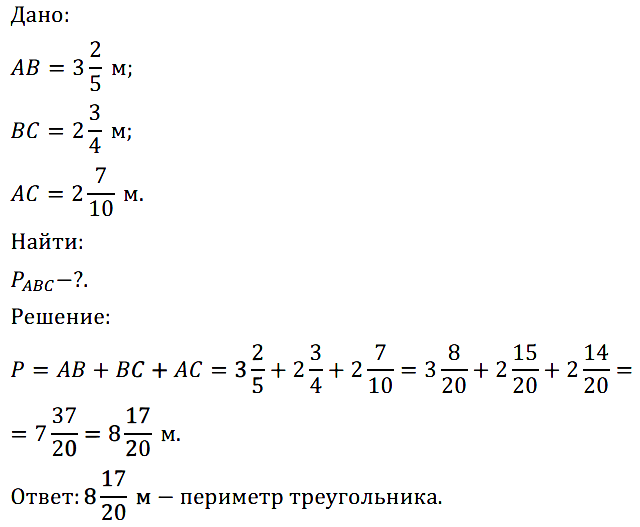
№ 395. На одной машине 4 7 /₁₀ т груза, а на другой — на 1 2 /₅ т меньше. Сколько тонн груза на двух машинах?

№ 396. В одном ящике 5 3 /₁₀ кг винограда, что на 2 4 /₅ т кг меньше, чем в другом ящике. Сколько килограммов винограда в двух ящиках?

№ 397. На окраску оконных рам израсходовали 2 7 /₁₀ кг краски, на окраску пола пошло 10 19 /₂₀ кг, а на окраску дверей потребовалось на 4 3 /₅ кг меньше, чем на окраску пола. Сколько всего израсходовали краски?

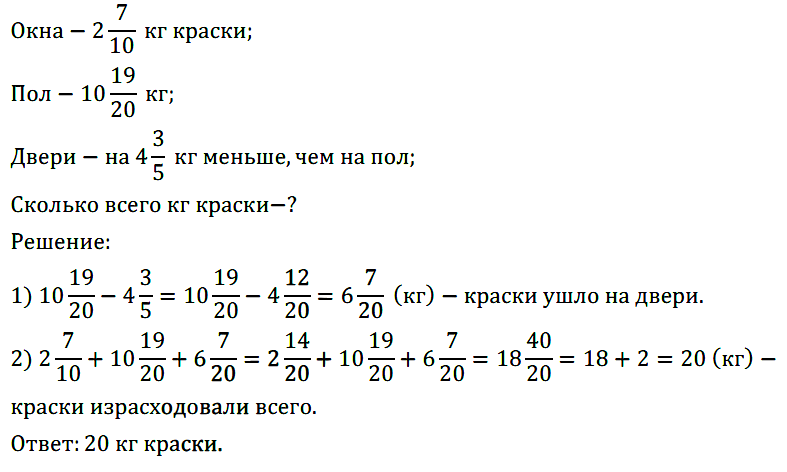
№ 398. Три бригады вырастили горох на площади 72 19 /₂₀ га. Первая и вторая бригады вырастили горох на площади 44 3 /₄ га, а вторая и третья — на площади 52 9 /₂₀ га. Найдите площадь каждого участка.

№ 399. На сахарный завод в понедельник привезли 212 1 /₂ т свёклы, во вторник — на 297 1 /₅ т больше, чем в понедельник, а в среду — на 114 2 /₅ т меньше, чем во вторник и понедельник вместе. Из 7 т свёклы получается 1 т сахара. Сколько сахара получится из привезённой свёклы?

№ 400. В трёх бидонах 10 л молока. В первом и втором бидонах было 6 3 /₄ л, а во втором и третьем — 5 1 /₃ л молока. Сколько литров молока было в каждом бидоне?

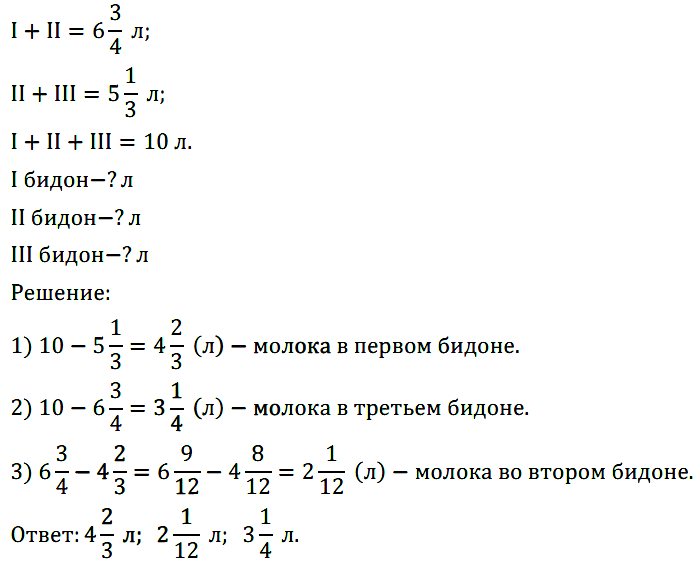
№ 401. Теплоход по течению реки проходит 33 3 /₈ км за 1 ч. Скорость течения 2 1 /₂ км/ч. Найдите скорость теплохода против течения.

№ 402. Скорость катера по течению реки 17 1 /₂ км/ч, а против течения 12 1 /₂ км/ч. Какова скорость течения?

№ 403. Федя и Вася шли навстречу друг другу. Каждый час расстояние между ними уменьшалось на 8 2 /₅ км. Найдите скорость Феди, если скорость Васи 3 1 /₂ км/ч.

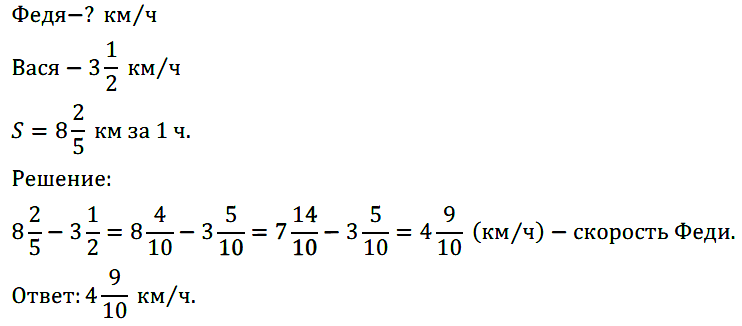
№ 404. Первый велосипедист догонял второго, причём расстояние между ними уменьшалось каждый час на 2 3 /₄ км. С какой скоростью ехал первый велосипедист, если второй ехал со скоростью 12 1 /₂ км/ч?

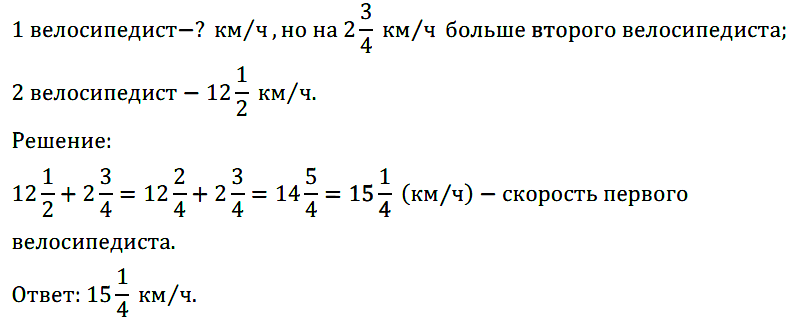
№ 405. Найдите значение выражения: а) 1 7 /₉ + 28 + 2 5 /₁₂ + 5 2 /₉ + 7/12 + 4 3 /₄; б) 5 3 /₅ – 3,15 + 7 12 /₂₅; …

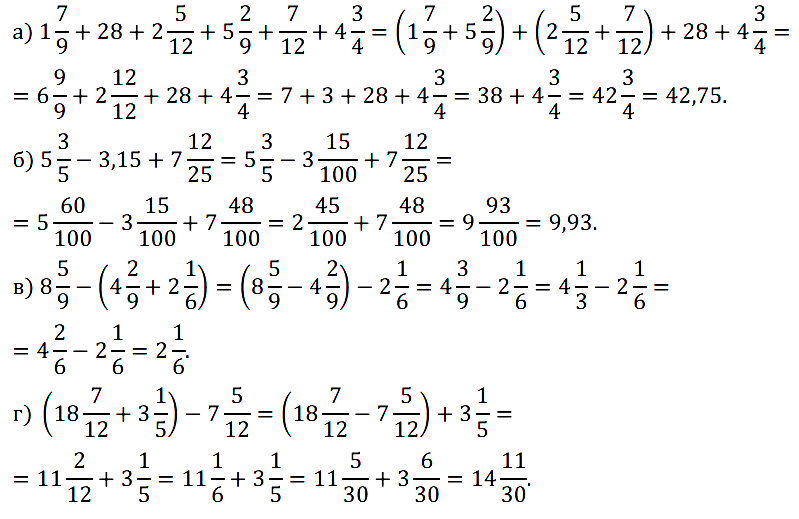
№ 406. Вычислите устно: а) 70 : 5 • 7 – 18 : 5 + 64 = ? …

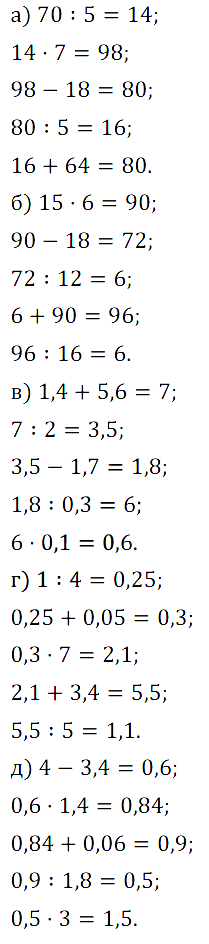
№ 407. Найдите пропущенные числа на рисунке: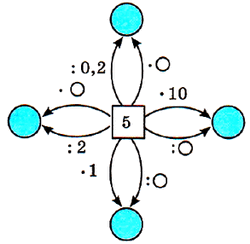

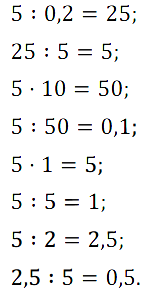
№ 408. Найдите натуральные значения m, при которых верно неравенство:
а) m/13 Нажмите на спойлер, чтобы увидеть ОТВЕТ

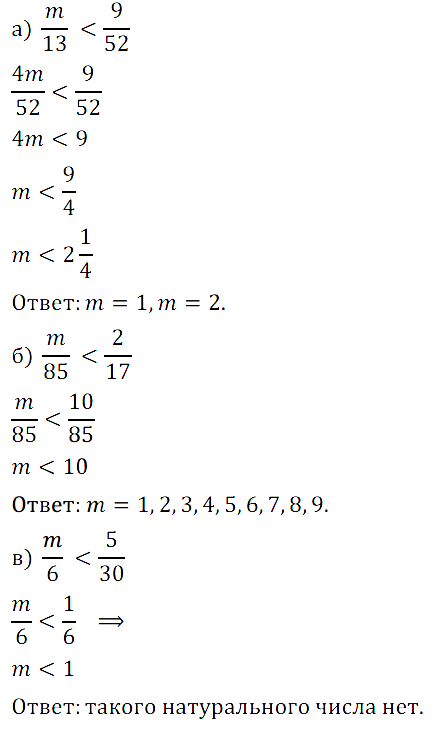
№ 409. На сколько процентов увеличится объём куба, если длину каждого его ребра увеличить на 20 %?

№ 410. Почтовый самолёт поднялся с аэродрома в 10 ч 40 мин утра, пробыл в полёте 5 ч 15 мин, а на земле во время стоянки 1 ч 37 мин. Когда самолёт вернулся на аэродром?

№ 411. Выполните действие: а) 5/6 – 3/4; б) 1/3 + 1/5; в) 3/10 + 1/2; …

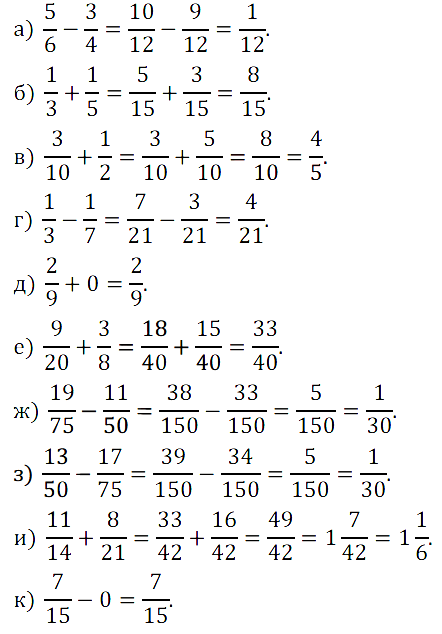
№ 412. Четырёхугольник с равными сторонами называют ромбом (рис. 18). Подумайте, является ли ромб правильным многоугольником. В чём сходство решения этой задачи с нахождением решений двойного неравенства 0 Нажмите на спойлер, чтобы увидеть ОТВЕТ

№ 413. Докажите переместительное и сочетательное свойства сложения для дробей с одинаковыми знаменателями на основе таких же свойств для натуральных чисел.

№ 414. Три сына хана получили в наследство большую отару овец. Старшему сыну достались 25 частей стада, среднему — 10 частей, а младшему — 1 часть. Сколько овец было в отаре, если средний брат получил на 765 овец больше, чем младший?

№ 415. В городе семизначные телефонные номера. Сколько в нём может быть номеров, начинающихся цифрами 235?

№ 416. Выполните вычисления с помощью микрокалькулятора и результат округлите до тысячных: 3,281 • 0,57 + 4,356 • 0,278 – 13,758 : 6,83.

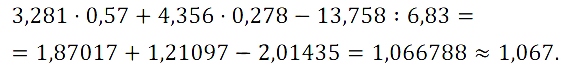
№ 417. Решите задачу:
1) Для борьбы с вредителями садов готовится известково–серный отвар, состоящий из 6 частей серы, 3 частей негашёной извести и 50 частей воды (по массе). Сколько получится килограммов отвара, если воды взять на 8,8 кг больше, чем серы?
2) Для приготовления фарфора на 1 часть гипса берут 2 части песка и 25 частей глины (по массе). Сколько получится килограммов фарфора, если взять глины на 6,9 кг больше, чем песка?

№ 418. Выполните действия:
1) 7225 : 85 + 64 • 2345 – 248 838 : 619;
2) 54 • 3465 – 9025 : 95 + 360 272 : 712.

№ 419. Выполните действие: а) 91 1 /₆ +3 5 /₁₈; б) 1 4 /₁₅ + 2 3 /₂₀; в) 5 1 /₈ + 41 7 /₁₂; …

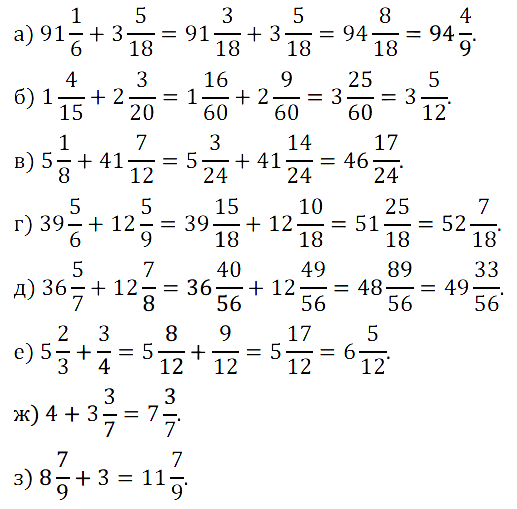
№ 420. Найдите значение разности: а) 1 – 8/15; б) 3 – 2/11; в) 4 – 3 4 /₉; …

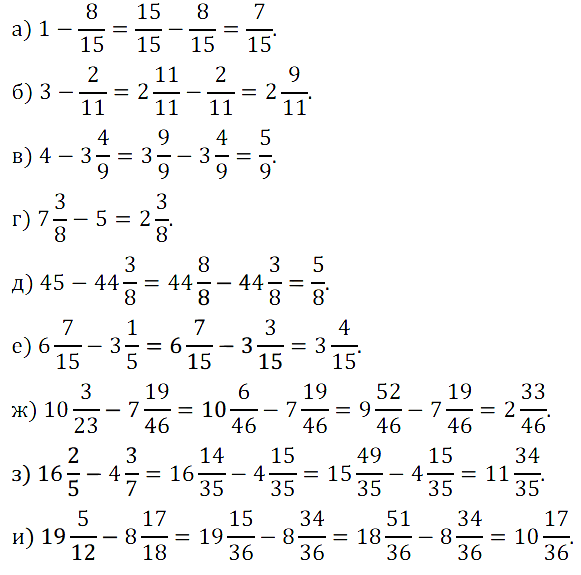
№ 421. Решите уравнение: а) 1 – k = 3/5 + 1/10; б) t + 1 = 4/9 + 2/3; в) x + 2 3 /₈ = 5 1 /₄ – 1 3 /₈.

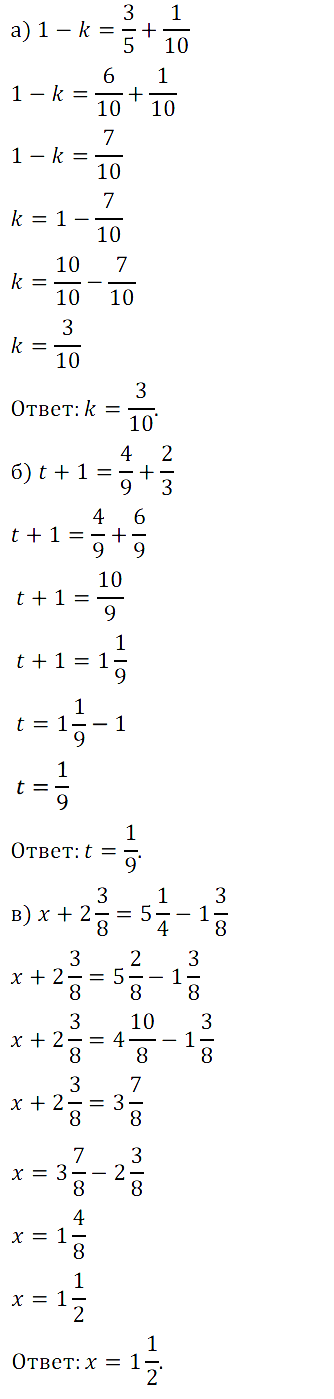
№ 422. Найдите значение выражения: а) 3 5 /₁₆ + 1/4 – 2 1 /₁₆; б) 1/8 + 2 3 /₅ + 2 7 /₈; …

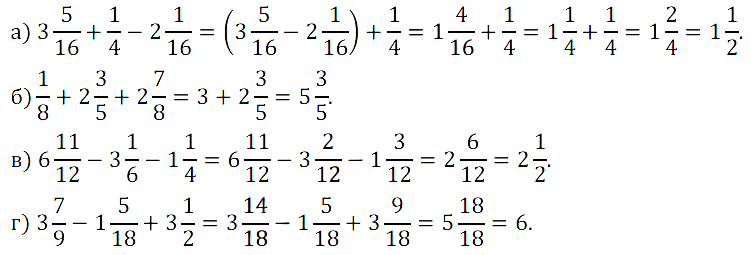
№ 423. Один тракторист вспахал 2/9 поля, а другой — 2/3 того же поля. Какую часть поля осталось вспахать?

№ 424. Бочки горючего хватает для работы одного двигателя на 7 ч, а другого — на 5 ч. Какая часть горючего останется от полной бочки после 2 ч работы первого двигателя и 3 ч работы второго двигателя?

№ 425. Для экспедиции, работающей в тайге, сбросили с вертолёта упаковку с продуктами, которая упала на землю через 3 с. С какой высоты была сброшена эта упаковка, если в первую секунду она пролетела 4 9 /₁₀ м, а в каждую следующую секунду она пролетала на 9 4 /₅ м больше, чем в предыдущую?

№ 426. Сколько времени пошло на изготовление детали, если её обрабатывали на токарном станке 2 1 /₄ ч, на фрезерном станке 3 1 /₆ ч и на сверлильном станке 1 1 /₁₅ ч?

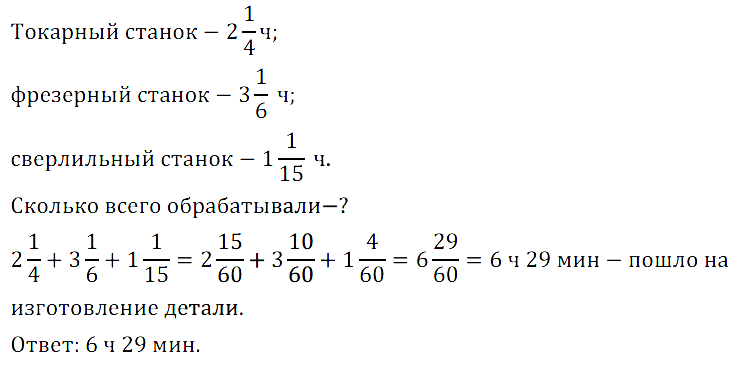
№ 427. Найдите значение выражения: а) 5,7 + 3 2 /₅ – 7 1 /₂; б) 3 7 /₁₅ + 4,6 – 1 2 /₃.

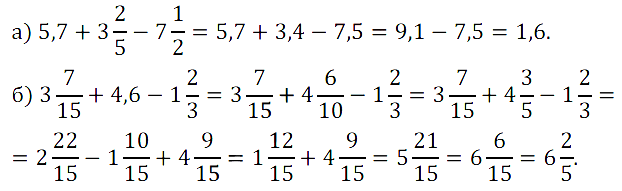
№ 428. Из одного пункта одновременно в противоположных направлениях вышли два пешехода. Через 1,5 ч расстояние между ними было 12,3 км. Скорость одного пешехода 4,4 км/ч. Найдите скорость другого пешехода.

№ 429. Для приготовления варенья из вишни на 3 части сахара берут 2 части ягод (по массе). Сколько килограммов сахара и сколько килограммов ягод надо взять, чтобы получить 10 кг варенья, если при варке его масса уменьшается в 1,5 раза?

№ 430. Найдите значение выражения:
а) (44,96 + 28,84 : (13,7 – 10,9)) : 1,8;
б) 102,816 : (3,2 • 6,3) + 3,84.

№ 431. Решите уравнение:
а) (х – 4,7) • 7,3 = 38,69; б) (3,6 – а) • 5,8 = 14,5; в) 23,5 – (2,3а + 1,2а) = 19,3; г) 12,98 – (3,8x – 1,3x) = 11,23.

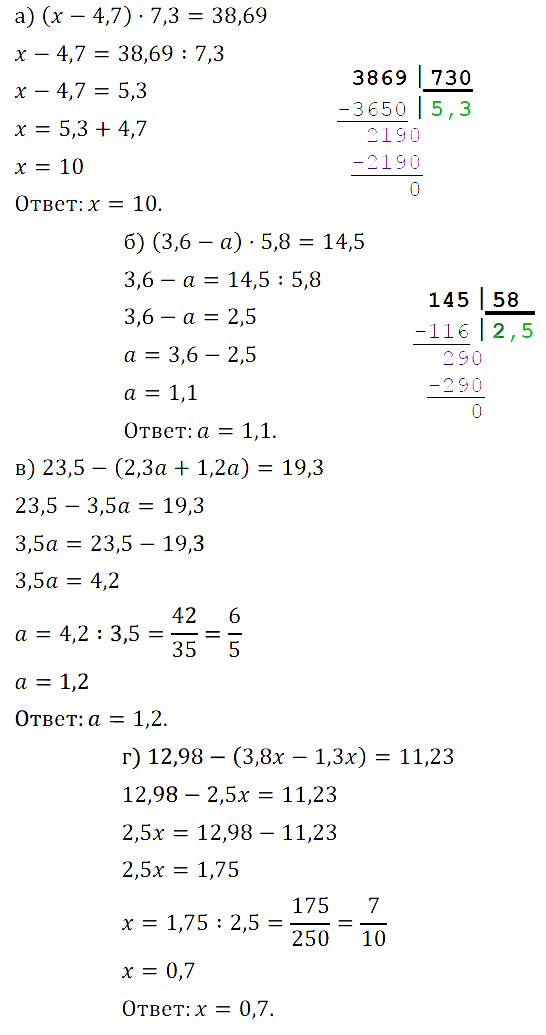
Вы смотрели: Упражнения по математике для УМК Виленкин с ответами на некоторые задачи. § 2. Сложение и вычитание дробей с разными знаменателями. 12. Сложение и вычитание смешанных чисел. Математика 6 Виленкин. Задачи 381-431 . ГДЗ по новому учебнику (Решебник упражнений).

Возведение в степень: правила, примеры

Мы разобрались, что вообще из себя представляет степень числа. Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. возводить числа в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя. Все определения будут проиллюстрированы примерами.

Понятие возведения в степень

Начнем с формулирования базовых определений.

Возведение в степень – это вычисление значения степени некоторого числа.

То есть слова “вычисление значение степени” и “возведение в степень” означают одно и то же. Так, если в задаче стоит “Возведите число 0 , 5 в пятую степень”, это следует понимать как “вычислите значение степени ( 0 , 5 ) 5 .

Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.

Как возвести число в натуральную степень

Вспомним, что такое степень числа с натуральным показателем. Для степени с основанием a и показателем n это будет произведение n -ного числа множителей, каждый из которых равен a . Это можно записать так:

Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.

Условие: возведите – 2 в степень 4 .

Решение

Используя определение выше, запишем: ( − 2 ) 4 = ( − 2 ) · ( − 2 ) · ( − 2 ) · ( − 2 ) . Далее нам нужно просто выполнить указанные действия и получить 16 .

Возьмем пример посложнее.

Вычислите значение 3 2 7 2

Решение

Данную запись можно переписать в виде 3 2 7 · 3 2 7 . Ранее мы рассматривали, как правильно умножать смешанные числа, упомянутые в условии.

Выполним эти действия и получим ответ: 3 2 7 · 3 2 7 = 23 7 · 23 7 = 529 49 = 10 39 49

Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности. Разберем пример.

Выполните возведение в квадрат числа π .

Решение

Для начала округлим его до сотых. Тогда π 2 ≈ ( 3 , 14 ) 2 = 9 , 8596 . Если же π ≈ 3 . 14159 , то мы получим более точный результат: π 2 ≈ ( 3 , 14159 ) 2 = 9 , 8695877281 .

Отметим, что необходимость высчитывать степени иррациональных чисел на практике возникает сравнительно редко. Мы можем тогда записать ответ в виде самой степени ( ln 6 ) 3 или преобразовать, если это возможно: 5 7 = 125 5 .

Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой:

Это понятно из записи .

От основания степени это не зависит.

Так, ( − 9 ) 1 = − 9 , а 7 3 , возведенное в первую степень, останется равно 7 3 .

Как возвести число в целую степень

Для удобства разберем отдельно три случая: если показатель степени – целое положительное число, если это ноль и если это целое отрицательное число.

В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. О том, как работать с такими степенями, мы уже рассказали выше.

Теперь посмотрим, как правильно возводить в нулевую степень. При основании, которое отличается от нуля, это вычисление всегда дает на выходе 1 . Ранее мы уже поясняли, что 0 -я степень a может быть определена для любого действительного числа, не равного 0 , и a 0 = 1 .

5 0 = 1 , ( – 2 , 56 ) 0 = 1 2 3 0 = 1

0 0 – не определен.

У нас остался только случай степени с целым отрицательным показателем. Мы уже разбирали, что такие степени можно записать в виде дроби 1 a z , где а – любое число, а z – целый отрицательный показатель. Мы видим, что знаменатель этой дроби есть не что иное, как обыкновенная степень с целым положительным показателем, а ее вычислять мы уже научились. Приведем примеры задач.

Возведите 2 в степень – 3 .

Решение

Используя определение выше, запишем: 2 – 3 = 1 2 3

Подсчитаем знаменатель этой дроби и получим 8 : 2 3 = 2 · 2 · 2 = 8 .

Тогда ответ таков: 2 – 3 = 1 2 3 = 1 8

Возведите 1 , 43 в степень – 2 .

Решение

Переформулируем: 1 , 43 – 2 = 1 ( 1 , 43 ) 2

Вычисляем квадрат в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом: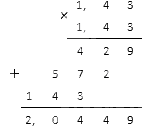

В итоге у нас вышло ( 1 , 43 ) – 2 = 1 ( 1 , 43 ) 2 = 1 2 , 0449 . Этот результат нам осталось записать в виде обыкновенной дроби, для чего необходимо умножить ее на 10 тысяч (см. материал о преобразовании дробей).

Ответ: ( 1 , 43 ) – 2 = 10000 20449

Отдельный случай – возведение числа в минус первую степень. Значение такой степени равно числу, обратному исходному значению основания: a – 1 = 1 a 1 = 1 a .

Пример: 3 − 1 = 1 / 3

9 13 – 1 = 13 9 6 4 – 1 = 1 6 4 .

Как возвести число в дробную степень

Для выполнения такой операции нам потребуется вспомнить базовое определение степени с дробным показателем: a m n = a m n при любом положительном a , целом m и натуральном n .

Таким образом, вычисление дробной степени нужно выполнять в два действия: возведение в целую степень и нахождение корня n -ной степени.

У нас есть равенство a m n = a m n , которое, учитывая свойства корней, обычно применяется для решения задач в виде a m n = a n m . Это значит, что если мы возводим число a в дробную степень m / n , то сначала мы извлекаем корень n -ной степени из а , потом возводим результат в степень с целым показателем m .

Проиллюстрируем на примере.

Вычислите 8 – 2 3 .

Решение

Способ 1. Согласно основному определению, мы можем представить это в виде: 8 – 2 3 = 8 – 2 3

Теперь подсчитаем степень под корнем и извлечем корень третьей степени из результата: 8 – 2 3 = 1 64 3 = 1 3 3 64 3 = 1 3 3 4 3 3 = 1 4

Способ 2. Преобразуем основное равенство: 8 – 2 3 = 8 – 2 3 = 8 3 – 2

После этого извлечем корень 8 3 – 2 = 2 3 3 – 2 = 2 – 2 и результат возведем в квадрат: 2 – 2 = 1 2 2 = 1 4

Видим, что решения идентичны. Можно пользоваться любым понравившимся способом.

Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью. Для простоты вычислений его лучше заменить обычной дробью и считать, как указано выше.

Возведите 44 , 89 в степень 2 , 5 .

Решение

Преобразуем значение показателя в обыкновенную дробь: 44 , 89 2 , 5 = 44 , 89 5 2 .

А теперь выполняем по порядку все действия, указанные выше: 44 , 89 5 2 = 44 , 89 5 = 44 , 89 5 = 4489 100 5 = 4489 100 5 = 67 2 10 2 5 = 67 10 5 = = 1350125107 100000 = 13 501 , 25107

Ответ: 13 501 , 25107 .

Если в числителе и знаменателе дробного показателя степени стоят большие числа, то вычисление таких степеней с рациональными показателями – довольно сложная работа. Для нее обычно требуется вычислительная техника.

Отдельно остановимся на степени с нулевым основанием и дробным показателем. Выражению вида 0 m n можно придать такой смысл: если m n > 0 , то 0 m n = 0 m n = 0 ; если m n 0 нуль остается не определен. Таким образом, возведение нуля в дробную положительную степень приводит к нулю: 0 7 12 = 0 , 0 3 2 5 = 0 , 0 0 , 024 = 0 , а в целую отрицательную – значения не имеет: 0 – 4 3 .

Как возвести число в иррациональную степень

Необходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считают на компьютере из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.

Если нам нужно вычислить значение степени a с иррациональным показателем a , то мы берем десятичное приближение показателя и считаем по нему. Результат и будет приближенным ответом. Чем точнее взятое десятичное приближение, тем точнее ответ. Покажем на примере:

Вычислите приближенное значение 2 в степени 1,174367.

Решение

Ограничимся десятичным приближением a n = 1 , 17 . Проведем вычисления с использованием этого числа: 2 1 , 17 ≈ 2 , 250116 . Если же взять, к примеру, приближение a n = 1 , 1743 , то ответ будет чуть точнее: 2 1 , 174367 . . . ≈ 2 1 , 1743 ≈ 2 , 256833 .