Тригонометрические функции

В школьной программе изучаются четыре тригонометрических функции – синус, косинус, тангенс и котангенс. В этой статье мы рассмотрим графики и основные свойства этих функций.

1. Начнем с построения графика функции y = sin x.

Выберем подходящий масштаб. По оси X: три клетки примем за (это примерно полтора). Тогда – одна клеточка, – две клетки.
По оси Y : две клетки примем за единицу.

Область определения функции y = sin x – все действительные числа, поскольку значение sin α можно посчитать для любого угла α.

Вспомним, что у нас есть тригонометрический круг, на котором обозначены синусы и косинусы основных углов. Удобнее всего отметить на будущем графике точки, в которых значение синуса является рациональным числом.

Можем добавить, для большей плавности графика, точки и . В них значение синуса равно
Соединим полученные точки плавной кривой.

Мы помним, что . Это значит, что
Получается часть графика, симметричная той, которую нарисовали раньше.

Кроме того, значения синуса повторяются через полный круг или через целое число кругов, то есть

Это значит, что функция y = sin x является периодической. Мы уже построили уча-сток графика длиной 2π. А теперь мы как будто “копируем” этот участок и повторяем его с периодом 2π:

Синусоида построена.
Перечислим основные свойства функции y = sin x.

1) D(y): x ∈ R, то есть область определения – все действительные числа.

2) E(y): y ∈ [−1; 1]. Это означает, что наибольшее значение функции y = sin x равно единице, а наименьшее – минус единице.

3) Функция y = sin x – нечетная. Ее график симметричен относительно нуля.

4) Функция y = sin x – периодическая. Ее наименьший положительный период равен 2π.

2. Следующий график: y = cos x. Масштаб – тот же. Отметим на графике точки, в которых косинус является рациональным числом:

Поскольку cos (−x) = cos x, график будет симметричен относительно оси Y , то есть левая его часть будет зеркальным отражением правой.

Функция y = cos x – тоже периодическая. Так же, как и для синуса, ее значения повторяются через 2πn. “Копируем” участок графика, который уже построили, и повторяем периодически.

Перечислим основные свойства функции y = cos x.

1) D(y): x ∈ R, то есть область определения – все действительные числа.

2) E(y): y ∈ [−1; 1]. Это означает, что наибольшее значение функции y = cos x равно единице, а наименьшее – минус единице.

3) Функция y = cos x – четная. Ее график симметричен относительно оси Y .

4) Функция y = cos x – периодическая. Ее наименьший положительный период равен 2π.

Отметим еще одно свойство. Графики функций y = sin x и y = cos x весьма похожи друг на друга. Можно даже сказать, что график косинуса получится, если график синуса сдвинуть на влево. Так оно и есть – по одной из формул приведения, .

Форма графиков функций синус и косинус, которые мы построили, очень характерна и хорошо знакома нам. Такой линией дети рисуют волны. Да, это и есть волны!

Функции синус и косинус идеально подходят для описания колебаний и волн – то есть процессов, повторяющихся во времени.

По закону синуса (или косинуса) происходят колебания маятника или груза на пружине. Переменный ток (тот, который в розетке) выражается формулой I(t) = I cos(ωt+α). Но и это не все. Функции синус и косинус описывают звуковые, инфра– и ультразвуковые волны, а также весь спектр электромагнитных колебаний. Ведь то, что наш глаз воспринимает как свет и цвет, на самом деле представляет собой электромагнитные колебания. Разные длины волн света воспринимается нами как разные цвета. Наши глаза видят лишь небольшую часть спектра электромагнитных волн. Кроме видимого цвета, в нем присутствуют радиоволны, тепловое (инфракрасное) излучение, ультрафиолетовое, рентгеновское и гамма–излучение. Более того – объекты микромира (например, электрон) проявляют волновые свойства.

3. Перейдем к графику функции y = tg x.

Чтобы построить его, воспользуемся таблицей значений тангенса. Масштаб возьмем тот же – три клетки по оси X соответствуют , две клетки по Y – единице. График будем строить на отрезке от 0 до π. Поскольку tg (x + πn) = tg x, функ-ция тангенс также является периодической. Мы нарисуем участок длиной π, а затем периодически его повторим.

Непонятно только, как быть с точкой . Ведь в этой точке значение тангенса не определено. А как же будет вести себя график функции y = tg x при x, близких к , то есть к 90 градусам?

Чтобы ответить на этот вопрос, возьмем значение x, близкое к , и посчитаем на калькуляторе значения синуса и косинуса этого угла. Пусть .

Синус угла – это почти 1. Точнее, sin = 0,9998. Косинус этого угла близок к нулю. Точнее, cos = 0,0175.

Тогда
график уйдет на 59 единиц (то есть на 118 клеток) вверх. Можно сказать, что если x стремится к (то есть к , значение функции y = tg x стремится к бесконечности .

Аналогично, при x, близких к , график тангенса уходит вниз, то есть стремится к минус бесконечности .

Осталось только “скопировать” этот участок графика и повторить его с периодом π.

Перечислим свойства функции y = tg x.

1) .
Другими словами, тангенс не определен для где n ∈ Z.
2) Область значений E(y) – все действительные числа.

3) Функция y = tg x – нечетная. Ее график симметричен относительно начала координат.

4) Функция y = tg x – периодическая. Ее наименьший положительный период равен π.

5) Функция y = tg x возрастает при то есть на каждом участке, на котором она непрерывна.

4. График функции y = ctg x строится аналогично. Вот он:

1) .
Другими словами, котангенс не определен для где n ∈ Z.
2) Область значений E(y) – все действительные числа.

3) Функция y = сtg x – нечетная. Ее график симметричен относительно начала координат.

4) Функция y = сtg x – периодическая. Ее наименьший положительный период равен π.

5) Функция y = сtg x убывает при то есть на каждом участке, на котором она непрерывна.

Построение графиков функций

О чем эта статья:

11 класс, ЕГЭ/ОГЭ

Понятие функции

Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
Графический способ — наглядно.
Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
Словесный способ.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида область определения выглядит так

х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Понятие графика функции

Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.

График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.

Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.

Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.

В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.

Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).

Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:

Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.

Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.

Исследование функции

Важные точки графика функции y = f(x):

стационарные и критические точки;
точки экстремума;
нули функции;
точки разрыва функции.

Стационарные точки — точки, в которых производная функции f(x) равна нулю.

Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.

Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.

Нули функции — это значения аргумента, при которых функция равна нулю.

Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.

Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:

Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.

Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.

Схема построения графика функции:

У нас есть отличные онлайн занятия по математике для учеников с 1 по 11 классы! Приходи на пробное занятие с нашими лучшими преподавателями!

Построение графика функции

Чтобы понять, как строить графики функций, потренируемся на примерах.

Задача 1. Построим график функции

Упростим формулу функции:

при х ≠ -1.

График функции — прямая y = x – 1 с выколотой точкой M (-1; -2).

Задача 2. Построим график функции

Выделим в формуле функции целую часть:

График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции

Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.

Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.

Вспомним, как параметры a, b и c определяют положение параболы.

Ветви вниз, следовательно, a 0.

Точка пересечения с осью Oy — c = 0.

Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.

Ветви вниз, следовательно, a 0.

Координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b

x	y
	-1
1	2

Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.

x	y
	2
1	1

k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.

x	y

1	2

k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.

k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.

Задача 5. Построить график функции

Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.

Нули функции: 3, 2, 6.

Промежутки знакопостоянства функции определим с помощью метода интервалов.

Вертикальные асимптоты: x = 0, x = 4.

Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.

Вот так выглядит график:

Задача 6. Построить графики функций:

б)

г)

д)

Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.

а)

Преобразование в одно действие типа f(x) + a.

Сдвигаем график вверх на 1:

б)

Преобразование в одно действие типа f(x – a).

Сдвигаем график вправо на 1:

В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x – a), затем сложение f(x) + a.

Сдвигаем график вправо на 1:

Сдвигаем график вверх на 2:

г)

Преобразование в одно действие типа

Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:

д)

Мы видим три преобразования вида f(ax), f (x + a), -f(x).

Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.

Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:

Синусоида формула, основные свойства кривой, построение графика тригонометрической функции, область определения

Все углы А по умолчанию приведены в градусах. Все таблицы значений и формулы синусов, косинусов, тангенсов, котангенсов (здесь). Во всех формулах пределов и разложений в ряд – углы в радианах.

Графики функций y=sinA, y=cosA, y=tgA,построенные для диапазона от 0 o до 360 o , показаны на рисунках ниже.

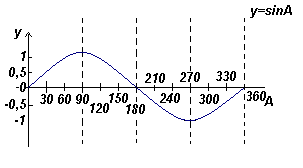График функции y=sinA (синусоида)	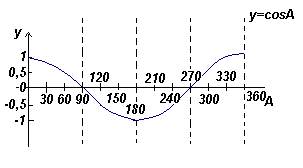График функции y=cosA (косинусоида)
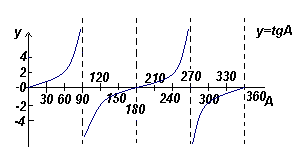График функции y=tgA (тангенсоида)

Из графиков видно что:

Графики синуса и косинуса колеблются в пределах между -1 и 1
Кривая косинуса имеет ту же форму, что и кривая синуса, но сдвинута относительно нее на 90 o
Кривые синуса и косинуса непрерывны и повторяются с периодом 360 o , кривая тангенса имеет разрывы и повторяется с периодом 180 o .

Углы произвольной величины

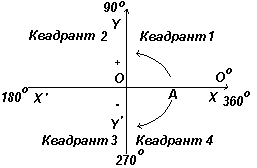На рис. слева показаны перпендикулярные оси ХХ’ и YY’; пересекающиеся в начале координат О. При работе с графиками измерения вправо и вверх от О считаются положительными, влево и вниз от О – отрицательными. Пусть ОА свободно вращается относительно О. При повороте ОА против часовой стрелки измеряемый угол считается положительным, а при повороте по часовой стрелке – отрицательным.

График. Положительное или отрицательное направление при движении по окружности.

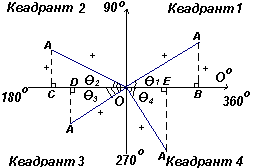Пусть ОА вращается против часовой стрелки таким образом, что Θ₁ – любой угол в первом квадранте, и построим перпендикуляр АВ для получения прямоугольного треугольника ОАВ на рис. слева. Поскольку все три стороны треугольника положительны, тригонометрические функции синус, косинус и тангенс в первом квадранте будут положительны. (Отметим, что длина ОА всегда положительна, поскольку является радиусом круга.)
Пусть ОА вращается дальше таким образом, что Θ₂ – любой угол во втором квадранте, и построим АС так, чтобы образовался прямоугольный треугольник ОАС. Тогда sin Θ₂=+/+ = +; cos Θ₂=+/- = -; tg Θ₂=+/- = -. Пусть ОА вращается дальше таким образом, что Θ₃ – любой угол в третьем квадранте, и построим АD так, чтобы образовался прямоугольный треугольник ОАD. Тогда sin Θ₃= -/+ = -; cos Θ₃= -/+ = -; tg Θ₃ = -/- =+ .

График. Поcтроение углов в различных квадрантах.

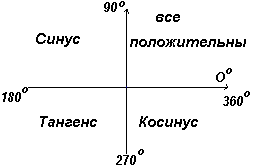Пусть ОА вращается дальше таким образом, что Θ₄– любой угол в четвертом квадранте, и построим АЕ так, чтобы образовался прямоугольный треугольник ОАЕ. Тогда sin Θ₄= -/+= -; cos Θ₄=+/+=+; tg Θ₄= -/+= -.

В первом квадранте все тригонометрические функции имеют положительные значения, во втором положителен только синус, в третьем – только тангенс, в четвертом только косинус, что и показано на рис. слева.

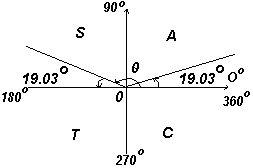
Знание углов произвольной величины необходимо при нахождении, например, всех углов между 0 o и 360 o , синус которых равен, скажем, 0,3261. Если ввести в калькулятор 0,3261 и нажать кнопку sin -1 , получим ответ 19,03 o . Однако существует второй угол между 0 o и 360 o , который калькулятор не покажет. Синус также положителен во втором квадранте. Другой угол показан на рис. ниже как угол Θ, где Θ=180 o – 19,03 o = 160,97 o . Таким образом, 19,03 o и 160,97 o – это углы в диапазоне от 0 o до 360 o , синус которых равен 0,3261.

Будьте внимательны! Калькулятор дает только одно из этих значений. Второе значение следует определить согласно теории углов произвольной величины.
График. Нахождение всех углов по заданному значению синуса (пример)

Пример 1

Найти все углы в диапазоне от 0 o до 360 o , синус которых равен -0,7071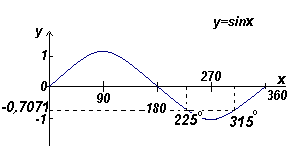

Решение:
Углы, синус которых равен -0,7071 o находятся в третьем и четвертом квадранте, поскольку синус отрицателен в этих квадрантах (смотри рис. слева).

График. Нахождение всех углов по заданному значению синуса (пример)

Из следующего рисунка Θ = arcsin 0,7071 = 45 o . Два угла в диапазоне от 0 o до 360 o , синус которых равен -0,7071, это 180 o +45 o =225 o и 360 o – 45 o = 315 o .

Примечание. Калькулятор дает только один ответ.
График. Нахождение всех углов по заданному значению синуса (пример)

Пример 2

Найти все углы между 0 o и 360 o , тангенс которых равен 1, 327.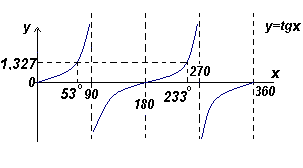

Решение:
Тангенс положителен в первом и третьем квадрантах – рис. слева.
График. Нахождение всех углов по заданному значению тангенса (пример)

Из рис ниже Θ = arctg1,327= 53 o .
Два угла в диапазоне от 0 o до 360 o , тангенс которых равен 1,327, это 53 o и 180 o + 53 o , т.е. 233 o .
График. Нахождение всех углов по заданному значению тангенса (пример)

Построение синусоиды и косинусоиды

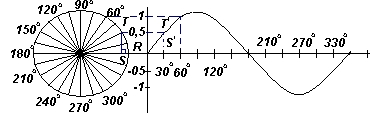
Пусть ОR на рис. слева- это вектор единичной длины, свободно вращающийся против часовой стрелки вокруг О. За один оборот получается круг, показанный на рис. и разделенный секторами по 15 o . Каждый радиус имеет горизонтальную и вертикальную составляющую. Например, для 30 o вертикальная составляющая – это ТS, а горизонтальная – ОS.

График. Построение синусоиды.

Из определения тригонометрических функций
sin30 o =TS/TO=TS/1, т.е. TS= sin30 o и cos30 o =OS/TO=OS/1, т.e. OS=cos30 o

Вертикальную составляющую TS можно перенести на график в виде T’S’, что равно значению, соответствующему углу 30 o на графике зависимости y от угла х. Если все вертикальные составляющие, подобно TS, перенести на график, то получится синусоида, показанная на рис. выше.

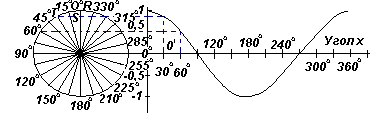
Если все горизонтальные составляющие, подобные OS, спроецировать на график зависимости у от угла х, получится косинусоида. Эти проекции легко визуализировать, перерисовывая круг с радиусом OR и началом отсчета углов от вертикали, как показано на рисунке слева.
Из рис. слева видно, что синусоида имеет ту же форму, что и косинусоида, но смещенная на 90 o .
График. Построение косинусоиды.

Синусоидальные и косинусоидальные графики

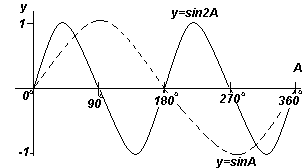График. y=sinA и y=sin2A (синусоиды).	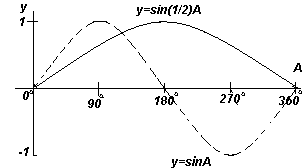График. y=sinA и y=sin(1/2)A (синусоиды).
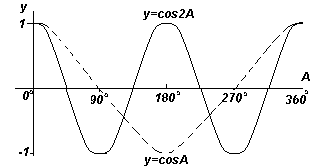График. y=cosA и y=cos2A (косинусоиды).	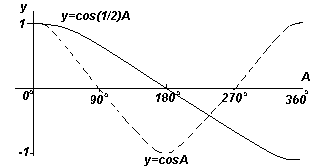График. y=cosA и y=cos(1/2)A (косинусоиды).

Периодические функции и период
Каждый из графиков функций, показанных на четырех рис. выше, повторяется при увеличении угла А, поэтому их называют периодическими функциями.
Функции y=sinA и y=cosA повторяются через каждые 360 o (или 2π радиан), поэтому 360 o называется периодом этих функций. Функции y=sin2A и y=cos2A повторяются через каждые 180 o (или π радиан),поэтому 180 o – это период для данных функций.
В общем случае если y=sinpA и y=cospA (где р – константа), то период функции равен 360 o /p (или 2π/p радиан ). Следовательно, если y=sin3A, то период этой функции равен 360 o /3= 120 o , если y=cos4A, то период этой функции равен 360 o /4= 90 o .

Амплитуда
Амплитудой называется максимальное значение синусоиды. Каждый из графиков 1-4 имеет амплитуду +1 (т.е. они колеблются между +1 и -1). Однако, если y=4sinA, каждая из величин sinA умножается на 4, таким образом, максимальная величина амплитуды – 4. Аналогично для y=5cos2A амплитуда равна 5, а период – 360 o /2= 180 o .

Пример 3.
Построить y=3sin2A в диапазоне от А= 0 o до А=360 o .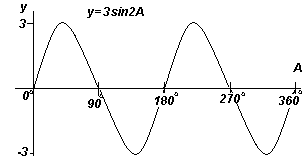

Решение:
Амплитуда =3, период = 360 o /2 =180 o .
График. Построение y=3sin2A (синусоида).

Пример 4.
Построить график y=4cos2x в диапазоне от х=0 o до х=360 o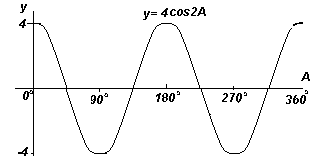

Решение:
Амплитуда = 4. период = 360 o /2 =180 o .

График. Построение y=4cos2x (косинусоида).

Углы запаздывания и опережения
Кривые синуса и косинуса не всегда начинаются в 0 o . Чтобы учесть это обстоятельство, периодическая функция представляется в виде y=sin(A± α), где α – сдвиг фазы относительно y=sinA и y=cosA.

o ) (синусоида).” name=”sin(A-60)” src=”https://www.dpva.ru/netcat_files/Image/GuideMathematics/TrigonometricCurves/sin(A-60).gif” style=”float: left; width: 311px; height: 168px;” title=”График. y=sin(A-60o) (синусоида).” />Составив таблицу значений, можно построить график функции y=sin(A-60 o ), показанный на рис. слева. Если кривая y=sinA начинается в 0 o , то кривая y=sin(A-60 o ) начинается в 60 o (т.е. ее нулевое значение на 60 o правее ). Таким образом, говорят, что y=sin(A-60 o ) запаздывает относительно y=sinA на 60 o .
График. y=sin(A-60 o ) (синусоида).

o ) (косинусоида).” name=”cos(A+45)” src=”https://www.dpva.ru/netcat_files/Image/GuideMathematics/TrigonometricCurves/cos(A+45).gif” style=”float: left; width: 311px; height: 168px;” title=”График. y=cos(A+45o) (косинусоида).” /> Составив таблицу значений, можно построить график функции y=cos(A+45 o ), показанный на рис. ниже.
Если кривая y=cosA начинается в 0 o , то кривая y=cos(A+45 o ) начинается на 45 o левее (т.е. ее нулевая величина находится на 45 o раньше ).
Таким образом, говорят, что график y=cos(A+45 o ) опережает график y=cosA на 45 o .
График. y=cos(A+45 o ) (косинусоида).

В общем виде, график y=sin(A-α) запаздывает относительно y=sinAна угол α.
Косинусоида имеет ту же форму, что и синусоида, но начинается на 90 o левее, т.е. опережает ее на 90 o . Следовательно, cosA=sin(A+90 o ).

Пример 5.
Построить график y=5sin(A+30 o ) в диапазоне от А=0 o до А=360 o

o ) (синусоида).” name=”5sin(A+30)” src=”https://www.dpva.ru/netcat_files/Image/GuideMathematics/TrigonometricCurves/5sin(A+30).gif” style=”float: left; width: 311px; height: 168px;” title=”График. y=cos(A+45o) (косинусоида).” />
Решение:
Амплитуда = 5, период = 360 o /1 = 360 o .
5sin(A+30 o ) опережает 5sinA на 30 o т.е. начинается на 30 o раньше.
График y=5sin(A+30 o ) (синусоида).

Пример 6.
Построить график y=7sin(2A-π/3) в диапазоне от А=0 o до А=360 o .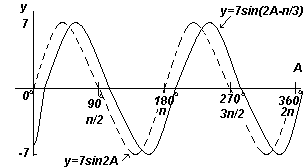

Решение:
Амплитуда = 7, период =2π/2= π радиан
В общем случае y=sin(pt-α) запаздывает относительно y=sinpt на α/p, следовательно 7sin(2A-π/3) запаздывает относительно 7sin2A на ( π/3)/2, т.е. на π/6 радиан или на 30 o
График. y=7sin2A и y=7sin(2A-п/3) (синусоиды).

Синусоида вида Asin(ωt±α). Фазовый угол. Сдвиг по фазе.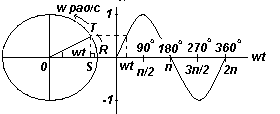

Пусть OR на рис. слева представляет собой вектор, свободно вращающийся против часовой стрелки вокруг О со скоростью ω радиан/с. Вращающийся вектор называется фазовым вектором. Через время t секунд OR повернется на угол ωt радиан (на рис. слева это угол TOR). Если перпендикулярно к OR построить ST, то sinωt=ST/OT, т.e. ST=OTsinωt.
Если все подобные вертикальные составляющие спроецировать на график зависимости у от ωt, получится синусоида с амплитудой OR.
График. Фазовый угол. Сдвиг по фазе.

Если фазовый вектор OR делает один оборот (т.е. 2π радиан) за Т секунд, то угловая скорость ω=2π/Т рад/с, откуда
Т=2π/ ω (с), где
Т – это период
Число полных периодов, проходящих за 1 секунду, называется частотой f.
Частота = (количество периодов)/(секунда) = 1/ T = ω/2π Гц, т.е. f= ω/2π Гц
Следовательно, угловая скорость
ω=2πf рад/с.

Если в общем виде синусоидальная функция выглядит, как y=sin(ωt± α), то
А – амплитуда
ω – угловая скорость
2π/ ω – период Т, с
ω/2π – частота f, Гц
α – угол опережения или запаздывания (относительно y=Аsinωt ) в радианах, он называется также фазовым углом.

Пример 7.
Переменный ток задается как i=20sin(90πt+0,26) ампер. Определить амплитуду, период, частоту и фазовый угол (в градусах)

Решение:
i=20sin(90πt+0,26)А, следовательно,
амплитуда равна 20 А
угловая скорость ω=90π, следовательно,
период Т = 2π/ ω = 2π/ 90π = 0,022 с = 22мс
частота f = 1/Т = 1/0,022 = 45,46 Гц
фазовый угол α = 0,26 рад. = (0,26*180/π) o = 14,9 o .

Пример 8.
Колебательный механизм имеет максимальное смещение 3 м и частоту 55 Гц. Во время t=0 смещение составляет 100см. Выразить смещение в общем виде Аsin(ωt± α).

Решение
Амплитуда = максимальное смещение = 3м
Угловая скорость ω=2πf = 2π(55) = 110 πрад./с
Следовательно, смещение 3sin(110πt + α) м.
При t=0 смещение = 100см=1м.
Следовательно, 1= 3sin(0 + α), т.е. sinα=1/3=0,33
Следовательно α=arcsin0,33=19 o
Итак, смещение равно 3sin(110 πt + 0,33).

Пример 9.
Значение мгновенного напржения в схеме переменного тока в любые t секунд задается в виде v=350sin(40πt-0,542)В. Найти:
а) Амплитуду, период, частоту и фазовый угол (в градусах)
б) значение напряжения при t =0
в) значение напряжения при t =10 мс
г) время, за которое напряжение впервые достигнет значения 200 В.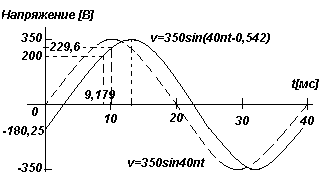
Решение:
а) Амплитуда равна 350 В, угловая скорость равна ω=40π
Следовательно,
период Т=2π/ ω=2π/40π=0,05 с =50мс
частота f=1/Т=1/0,05=20 Гц
фазовый угол = 0,542 рад (0,542*180/π) = 31 o с запаздыванием относительно v=350sin(40πt)
б) Если t =0, то v=350sin(0-0,542)=350sin(-31 o )=-180,25 В
в) Если t =10 мс, то v=350sin(40π10/10 3 -0,542)=350sin(0,714)=350sin41 o =229,6 В
г) Если v=200 И, то 200=350sin(40πt-0,542) 200/350=sin(40πt-0,542)

График. Колебательный механизм (пример, синусоида).

v=350sin(40πt-0,542) Следовательно, (40πt-0,542)=arcsin200/350=35 o или 0,611 рад.
40πt= 0,611+0,542=1,153.
Следовательно, если v=200В, то время t=1,153/40π=9,179 мс

Функция y = sin x, её свойства и график

п.1. Развертка ординаты движения точки по числовой окружности в функцию от угла

При движении точки по числовой окружности её ордината является синусом соответствующего угла (см. §2 данного справочника).

Рассмотрим, как изменяется синус, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=sinx на этом отрезке.

Если мы продолжим движение по окружности для углов x > 2π, кривая продолжится вправо; если будем обходить числовую окружность в отрицательном направлении (по часовой стрелке) для углов x синусоидой .
Часть синусоиды для 0≤x≤2π называют волной синусоиды .
Часть синусоиды для 0≤x≤π называют полуволной или аркой синусоиды .

п.2. Свойства функции y=sinx⁡

1. Область определения (xinmathbb) – множество действительных чисел.

2. Функция ограничена сверху и снизу

Область значений (yin[-1;1])

3. Функция нечётная

4. Функция периодическая с периодом 2π

5. Максимальные значения (y_=1) достигаются в точках

Минимальные значения (y_=-1) достигаются в точках

Нули функции (y_<0>=sinx_0=0) достигаются в точках (x_0=pi k)

6. Функция возрастает на отрезках

$$ -fracpi2+2pi kleq xleqfracpi2+2pi k $$

Функция убывает на отрезках

$$ fracpi2+2pi kleq xleqfrac<3pi><2>+2pi k $$

7. Функция непрерывна.

п.3. Примеры

Пример 1. Найдите наименьшее и наибольшее значение функции y=sinx на отрезке:

a) (left[fracpi6; frac<3pi><4>right]) $$ y_=sinleft(fracpi6right)=frac12, y_=sinleft(fracpi2right)=1 $$ б) (left[frac<5pi><6>; frac<5pi><3>right]) $$ y_=sinleft(frac<3pi><2>right)=-1, y_=sinleft(frac<5pi><6>right)=frac12 $$

Пример 2. Решите уравнение графически:
a) (sinx=3x)

Один корень: x = 0

б) (sinx=2x-2pi)

Один корень: x = π

в) (sinx-sqrt=0)
(sinx=sqrt)

Один корень: x = π

г*) (sinx=left(x-fracpi2right)^2-frac<4>)
(y=left(x-fracpi2right)^2-frac<4>) – парабола ветками вверх, с осью симметрии (x_0=fracpi2) и вершиной (left(fracpi2; -frac<4>right)) (см. §29 справочника для 8 класса)

Два корня: (x_1=0, x_2=pi)

Пример 3. Постройте в одной системе координат графики функций $$ y=sinx, y=-sinx, y=2sinx, y=sinx+2 $$

(y=-sinx) – отражение исходной функции (y=sinx) относительно оси OX. Область значений (yin[-1;1]).
(y=2sinx) – исходная функция растягивается в 2 раза по оси OY. Область значений (yin[-2;2]).
(y=sinx+2) – исходная функция поднимается вверх на 2. Область значений (yin[1;3]).

Пример 4. Постройте в одной системе координат графики функций $$ y=sinx, y=sin2x, y=sinfrac <2>$$

Амплитуда колебаний у всех трёх функций одинакова, область значений (yin[-1;1]).
Множитель под синусом изменяет период колебаний.
(y=sin2x) – период уменьшается в 2 раза, полная волна укладывается в отрезок (0leq xleq pi).
(y=sinfrac<2>) – период увеличивается в 2 раза, полная волна укладывается в отрезок (0leq xleq 4pi).

Тригонометрические функции, их свойства и графики
методическая разработка по алгебре (10 класс) на тему

Открытый урок в форме ФГОС

Скачать:

Вложение	Размер
organizatsionnaya_struktura_zanyatiya.docx	55.37 КБ
spetsialnost.docx	20.09 КБ
geometricheskie_preobrazovaniya_grafikov_trigonometricheskikh_funktsiy.doc	54.5 КБ
garmonika.pptx	550.63 КБ

Предварительный просмотр:

Организационная структура занятия

Учебный материал с указанием задания

Методы, приемы и формы обучения

Проверка присутствующих подготовка к работе

Подготовка к уроку

Проверка домашнего задания

Разбор на доске примеров из д.р., вызвавших затруднение

Актуализация опорных знаний, умений и навыков по данной теме .

Решите эти примеры, заполните таблицу, и вы узнаете, как называется график функции, которую мы сегодня будем изучать

Работа с презентацией (1), фронтальный опрос

Тема нашего урока « Тригонометрические функции и их графики»., мы узнаем как выглядит график тригонометрических функций, научимся строить эти графики, узнаем свойства этих ьфункцийСегодня на уроке мы с вами обобщим занятия и умения в построении графиков тригонометрических функций с помощью преобразований. Во время урока постепенно мы будем использоваться тот раздаточный материал, который находится у вас на партах».

А также узнаем, что такое волна, почему на рок концертах возрастает агрессивность и неадекватное поведение публики и что общего между качелями, звуком и красками

Мотивировать на конструктивную работу в течение урока

Отвечают на вопросы преподавателя

Объяснение нового материала.

(Рассказывая теорию, показываю соответствующие слайды из презентации). (Слайд 1) Откройте свои тетради, запишите число, сегодня 15.12.14, и тему занятия: «Свойства и графики тригонометрических функций». А работать мы будем по следующему плану (Слайд 2).

Как вы думаете, какие функции называются тригонометрическими?

Не совсем верно. Правильнее будет сказать: тригонометрическими функциями называются функции вида: y=sinx, y=cosx, y=tgx, y=ctgx. Запишите это определение.

(Слайд 3) Рассмотрим основополагающую тригонометрическую функцию y=sinx. Запишите подзаголовок: Свойства функции y=sinx и ее график. Для построения графика функции y=sinx, составим ее таблицу значений. Для каких углов синус легко определяется?

Составьте таблицу значений и напишите ее у себя в тетрадях. У каждого из вас лежат на столах листы, на которых начерчены системы координат (Приложение 1), отметим на первой системе координат полученные точки. Для удобства, возьмем за 3 ед. Соедините их, и получим график функции y=sinx (Слайд 4), так называемую синусоиду. С чем у вас ассоциируется график функции y=sinx? Да, вы правы. А знаете ли вы, что… Дальше учитель рассказывает исторические факты из создания теории тригонометрии. (Приложение 2).

Исследуем данный график. Посмотрите внимательно на график и скажите: Какова область определения данной функции? А область значения…? На каком промежутке функция y=sinx возрастает, а на каком убывает? Вы заметили, что функция снова возрастает и убывает через определенный промежуток? Значит, она обладает чем…? И каков же ее период? При каком значении х, у=0? Также эту функцию можно определить на четность или нечетность. Как вы думаете, какой функцией, четной или нечетной, она является и почему? Вот мы с вами и сформулировали основные свойства функции y=sinx. Запишите их в тетрадь (Слайд 5).

Отвечают: она бесконечна, т. е. х любое действительное число. А у принадлежит от -1 до 1.

Убывает на промежутке от до , а возрастает от – до .

Да. Периодом, он равен 2 .

Она является нечетной функцией, т. к. sin(-x)=-sinx

Слайд 6) Запишите следующий подзаголовок: «Свойства функции у=cosx и ее график».

Для построения графика функции у=cosx, воспользуемся формулой приведения cosx=sin( + x). Т. е. строим синусоиду, сдвинутую по оси Ох влево на…? Получим график функции у=cosx. Начертите эту функцию.

Рассказывает о происхождении понятия косинус (см. Приложение 2).

(Слайд 7) Т. к. график функции у=cosx, есть преобразованная синусоида, то и свойства функции у=cosx будут схожи со свойствами функции y=sinx. Запишите их, а затем найдите и назовите отличия.

1. убывает при х ;

2. возрастает при х ;

3. четная, т.к. cos(-x)=cosx;

Аналогично рассматривают пункты:

Свойства функции y=tgx и ее график
Свойства функции y=ctgx и ее график

(см. Слайд 8 – Слайд 12)

Работа с презентацией (2), Помощь в заполнении конспекта, визуальный контроль,

Наглядно-образные методы и приемы

Работа в тетрадях, построение графика синусоиды

Отвечают: sinx, cosx, tgx, ctgx

Записывают определение под диктовку учителя.

Записывают в тетради подзаголовок.

Составляют таблицу значений и пишут ее в тетрадях.

Отмечают на системе координат полученные точки, соединяют их и получают график функции y=sinx.

Отвечают: с волной на реке.

Записывают свойства функции в тетрадь.

Записывают новый подзаголовок.

Чертят на листах полученную функцию.

Первичное закрепление материала:

Решим несколько примеров для усвоения и закрепления полученных знаний. (Слайд 13).Устное решение примеров

2. (Первый пример решаю у доски, объясняю) Записывайте в тетрадь.

1.Найти множество значений функции а) y=2cosx

Следующий пример кто-нибудь у доски, остальные в тетради. (Вызываю к доске).

Второе задание направлено на определение четности и нечетности функции. Вспомним правило: Если y(-x) = y (x), то функция четная, а если y(-x) = -y (x), то функция нечетная.

y(-x)=(-x) 2 + cos(-x) = x 2 + cosx = = y(x) – четная

y(-x) = (-x) 3 – sin(-x) = -x 3 + sin x = = -(x 3 – sinx) = -y(x) – нечетная

А теперь научимся находить наименьший положительный период функции. Записывайте:

Работа со слайдами

Устная работа по презентации

Записывают. Отвечают на вопросы учителя в процессе решения.

Отвечают на вопросы учителя в процессе решения.

Выполнение упражнений из раздаточного материала с последующей проверкой, за правильно выполненные задания начисляются баллы

Помощь в решении примеров, визуальный контроль,

Практические методы, проблемная задача

Выполнение построения графика путем геометрических преобразований

Работа в парах, взаимопроверка

Презентации, подготовленные студентами «Тригонометрические функции в природе, технике», «Уравнение гармонических колебаний», «Гармоника в музыке»

Рефлексия. Проанализировать какие преобразования вызвали у вас затруднения, что понравилось и не понравилось на уроке, выявить причину неудавшихся упражнений,

посчитать количество баллов заработанных на уроке, выставить себе оценку, передать ее преподавателю .

Домашнее задание: продоллжитьпостроение графиков по листу-шаблону, нати период и множество значений полученных функций,

Предварительный просмотр:

Тригонометрические функции, их свойсива и графики

Актуальность использования ТСО

Визуализация материала, экономия времени на уроке, наглядность объяснения материала с помощью динамических моделей

Предполагается, что к окончанию урока учащиеся будут знать новый вид функции- тригонометрические.

Будут уметь оперировать математическими понятиями по этой теме, применять свойства функции для решения примеров

Урок способствует формированию коммуникативных навыков.

знать новый вид функций- тригонометрические, уметь различать их среди других функций , заданных графически и формулой, находить область определения и множество значений функции, строить график этих функций путем геометрических преобразований, показать применение функции в природе и жизни. Обеспечить усвоение свойств и графиков тригонометрических функций Установить связь между алгеброй и другими науками (геометрией, физикой, астрономией и т.д.).

Создание на уроке условий, обеспечивающих воспитание аккуратности и внимательности при выполнении работ с применением чертежных инструментов, способствование развитию творческого отношения к учебной деятельности, организация ситуаций, акцентирующих формирование сознательной дисциплины при работе, способствовать овладению необходимыми навыками самостоятельной учебной деятельности

Формировать умения учащихся исследовать тригонометрические функции;

Формировать умения учащихся строить графики тригонометрических функций.

Способствовать развитию умений учащихся обобщать полученные знания, проводить анализ, синтез, сравнения, делать необходимые выводы.Способствовать развитию абстрактного, логического, мышления.Обеспечить условия для овладения учащимися алгоритмом решения проблемных и исследовательских задач. Развивать познавательные процессы: умения наблюдать и обобщать, формулировать свойства, правила.

Развивать математическую речь.

Объяснительно-иллюстративный, частично-поисковый, приучения и упражнения

Тригонометрические формулы, определения синуса, косинуса и тангенса, построение графика путем геометрических преобразований, функции: нахождение D(f) и E(f)

Методическое оборудование занятия

Учебник, раздаточный материал для работы на уроке, мультимедийная презентация

з новый вид функции- тригонометрической, формулу, задающую функцию, различать ее среди других функций , заданных графически и формулой, знать свойства функции, ее применение в природе и жизни

По заданному графику функции восстановить формулу, задающую функцию и обратную задачу: по формуле построить график тригонометрической функции, строить график тригонометрической функции , заданной формулой путем геометрических преобразований; находить область определения и множество значений функции, сравнивать частные значения тригонометрической функции между собой и с единицей , решать задачи с практическим содержанием, применять свойства функции для нахождения нб и нм значения функции

Термины и понятия

График функции, значение функции и аргумента. Тригонометрические функция, их свойства. Параллельный перенос, растяжение (сжатие) в k раз, симметрия относительно оси, «неподвижные» точки графика

ГБПОУ СПО «МИПК им.И.Федорова»

Методическая разработка урока:

Тригонометрические функции, их свойства и графики

Преподаватель: Ромбах О.Б.

Предварительный просмотр:

Геометрические преобразования графиков тригонометрических функций

Предварительный просмотр:

Подписи к слайдам:

Что такое гармонический звук и как он влияет на человека

гармоническая составляющая, период которой равен периоду негармонического сигнала, называется первой или основной гармоникой сигнала. Все остальные составляющие называются высшими гармоническими составляющими. Гармоника, частота которой в k раз больше первой гармоники (а период, соответственно, в k раз меньше) , называется k – ой гармоникой. ГАРМОНИКА Гармония – чувство эстетического удовлетворения, обеспечиваемое равновесием (в. т. ч. душевным) и отсутствием внешних раздражителей.

Сущность музыкальной гармонии — проекция общеэстетического понятия гармонии на область звуковых явлений, объединяющая наиболее специфические для музыкального искусства художественные элементы и отношения: созвучия, ладовые функции и т. д. (тогда как, например, метр и ритм свойственны и поэзии) . Осознание благозвучности гармонически упорядоченных отношений звуков явилось величайшим завоеванием художественного мышления.

«Гармония» – одно из самых главных понятий музыкального искусства. Что же оно означает? Очевидно, слово «гармония» возникло далеко за пределами музыки: ведь люди издавна называли гармонией красоту и соразмерность, где бы она себя ни проявляла – в архитектурном ли сооружении, состоянии души или человеческой фигуре. Древние греки словом «гармония» определяли даже периоды мирной жизни, свободные от войн и потрясений. И это же слово – такое богатое смыслами, такое многозначное – из множества других было избрано для выражения глубинного смысла музыки, того главнейшего, что отличает ее от других видов искусства.

СПАСИБО ЗА ВНИМАНИЕ! Лебедева Анна группа 1КТ1

По теме: методические разработки, презентации и конспекты

Используемые технологии: дифференцированного обучения, критического мышления, коммуникативного общения, развивающее обучение. .

Применение интеграции в учебном процессе как способа развития аналитических и творческих способностей.

Презентация по теме функции и их свойства, чтение по графику функции.

Интегрированный урок математики и информатики.

Конспект урока в 10 классе. А.Н. Колмогоров.

Данная программа предназначена для повышения эффективности подготовки учащихся 11-х классов к итоговой аттестации по алгебре и началам анализа за курс полной средней школы и предусматривает их подгото.

Материалы могут быть использованы как для дистанционного обучения, так и самостоятельного исследования с последующей самопроверкой.

Геометрия. Урок 1. Тригонометрия

Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Тригонометрия в прямоугольном треугольнике

Тригонометрический круг

Основное тригонометрическое тождество

Таблица значений тригонометрических функций

Градусы и радианы

Формулы приведения

Теорема синусов

Расширенная теорема синусов

Теорема косинусов

Тригонометрические уравнения (10-11 класс)

Примеры решений заданий из ОГЭ

Тригонометрия в прямоугольном треугольнике

Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.

Синус угла – отношение противолежащего катета к гипотенузе.

sin α = Противолежащий катет гипотенуза

Косинус угла – отношение прилежащего катета к гипотенузе.

cos α = Прилежащий катет гипотенуза

Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).

tg α = Противолежащий катет Прилежащий катет

Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).

ctg α = Прилежащий катет Противолежащий катет

Рассмотрим прямоугольный треугольник A B C , угол C равен 90 °:

sin ∠ A = C B A B

cos ∠ A = A C A B

tg ∠ A = sin ∠ A cos ∠ A = C B A C

ctg ∠ A = cos ∠ A sin ∠ A = A C C B

sin ∠ B = A C A B

cos ∠ B = B C A B

tg ∠ B = sin ∠ B cos ∠ B = A C C B

ctg ∠ B = cos ∠ B sin ∠ B = C B A C

Тригонометрия: Тригонометрический круг

Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.

Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.

Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 )

На данной окружности будет три шкалы отсчета – ось x , ось y и сама окружность, на которой мы будем откладывать углы.

Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x , против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A . Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .

Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B ) и на ось игрек (точка C ) .

Отрезок O B является проекцией отрезка O A на ось x , отрезок O C является проекцией отрезка O A на ось y .

Рассмотрим прямоугольный треугольник A O B :

cos α = O B O A = O B 1 = O B

sin α = A B O A = A B 1 = A B

Поскольку O C A B – прямоугольник, A B = C O .

Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).

Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :

Опускаем из точки A перпендикуляры к осям x и y . Точка B в этом случае будет иметь отрицательную координату по оси x . Косинус тупого угла отрицательный .

Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x . (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y .

Координата по оси x – косинус угла , координата по оси y – синус угла .

Ещё одно замечание.

Синус тупого угла – положительная величина, а косинус – отрицательная.

Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный .

Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный .

Основное тригонометрическое тождество

sin 2 α + cos 2 α = 1

Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :

A B 2 + O B 2 = O A 2

sin 2 α + cos 2 α = R 2

sin 2 α + cos 2 α = 1

Тригонометрия: Таблица значений тригонометрических функций

Тригонометрия: градусы и радианы

Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!

Тригонометрия: Формулы приведения

Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,

можно заметить, что:

sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °

sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °

sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °

sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °

cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °

cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °

cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °

cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °

Рассмотрим тупой угол β :

Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:

sin ( 180 ° − α ) = sin α

cos ( 180 ° − α ) = − cos α

tg ( 180 ° − α ) = − tg α

ctg ( 180 ° − α ) = − ctg α

Тригонометрия: Теорема синусов

В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.

a sin ∠ A = b sin ∠ B = c sin ∠ C

Тригонометрия: Расширенная теорема синусов

Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R

Тригонометрия: Теорема косинусов

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A

b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B

c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с тригонометрией.

Тригонометрия: Тригонометрические уравнения

Это тема 10-11 классов.

Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!

Better Explained: Как понять ноль в нулевой степени?

В школе нас учат, что степень — это многократное умножение. Это прекрасно, но становится совсем непонятным, когда мы встречаем 3 1,5 или 0 0 .

Как мы можем повторить ноль нулевое количество раз и получить единицу? Всё дело в том, что наш подход к степени числа как к многократному умножению неверен. Нам нужно сменить парадигму. Давайте посмотрим, как мы привыкли воспринимать арифметические действия, и что они на самом деле из себя представляют.

Сложение

Как мы привыкли думать: это повторяющийся счёт

Как на самом деле: перемещение

Умножение

Как мы привыкли думать: это многократное сложение

Как на самом деле: масштабирование

Степень

Как мы привыкли думать: многократное умножение

Как на самом деле: рост с течением времени

Смотрим на арифметику как на преобразование

Отойдём на шаг назад. Как мы изучаем арифметику? Нас учат, что числа — это некое количество единиц; сложение — это прибавление одного количества единиц к другому количеству единиц (3+4 = 7), а умножение — это многократное сложение (2*3 = 2+2+2 = 6).

Многократное сложение прекрасно работает с круглыми числами, но что вы скажете про сложение чисел вроде -1 или 2²?

Очевидно, что эта модель восприятия неполноценна. Числа — это не просто единицы чего-то; гораздо лучше представлять их как некие точки с определённым положением на линии. Положение может быть отрицательным (-1), либо между другими числами (2²), либо в другом измерении (i).

Таким образом арифметика предстаёт перед нами как способ преобразовывать число. Сложение становится перемещением (+3 — это перемещение на 3 единицы вправо); умножение становится масштабированием (*3 — это увеличить число в три раза).

А что же такое тогда степень числа?

Познакомьтесь с Экпандотроном™

Это Экспандотрон 3000. Он выглядит как достаточно потрёпанная микроволновка, но вместо подогрева пищи она занимается ростом чисел. Просто положите число внутрь и проделайте несколько простых операций.

Начните с 1
Установите желаемый показатель «Роста» за одну секунду (2х, 3х, 10,3х и т.д.)
Установите желаемый показатель «Времени» в секундах
Нажмите кнопку START

Вуаля! После звукового сигнала достаём наше новенькое готовое число. Например, мы хотим изменить 1 на 9. Что нам нужно сделать?

Поместите 1 в Экспандотрон
Установите «Рост» на 3х, а «Время» на 2 секунды
Нажмите кнопку START

Что мы видим? Мы видим, как число начинает преобразовываться: 1; 1,1; 1,2. По окончании первой секунды оно уже выглядит как 3 и продолжает меняться: 3,1; 3,5; 4,0; 6,0; 7,5. И по окончании второй секунды оно превратилось в 9.

В математическом представлении Экспандотрон (или показательная функция) делает для нас следующее:

Например, 3 2 = 9/1. Основанием является то количество раз, в которое нам нужно вырастить число (х3), а степенью — количество времени (2). Формула типа 2 n означает «Используйте свой Экспандотрон на мощности х2 в течение n секунд».

Работу Экспандотрона мы всегда начинаем с 1, чтобы посмотреть, как он меняет одну единицу. Если мы хотим посмотреть, что случится с 3 в Экспандотроне, мы просто масштабируем конечный результат. Например:

Начните с 1 и умножьте на двойку в третьей степени: 1*2 3 = 1 * 2 * 2 * 2 = 8

Начните с 3 и умножьте на двойку в третьей степени: 3*2 3 = 3 * 2 * 2 * 2 = 24

Каждый раз, когда вы видите простую степень, вы начинаете с 1.

Идём к пониманию масштабирующего множителя

При умножении мы можем просто указать конечный масштабирующий множитель. Хотите число в 8 раз больше? Умножаем на 8. Готово.

Степени более капризны в обращении. Вот как они работают:

Вы: Хочу вырастить вот это число.

Экспандотрон: Ок, давай его сюда.

Вы: И насколько большим оно станет?

Экспандотрон: Пффф, без понятия. Давай посмотрим.

Вы: Посмотрим? Я думал, ты зна.

Экспандотрон: Тихо! Оно растёт! Растёт!

Экспандотрон: Готово! Это шедевр!

Экспандотрон не прямолинеен. Вы смотрите на него, но не знаете, что он сделает. Что значит 3 10 ? Степень числа вместо простого масштабирования заставляет нас почувствовать всеми органами процесс роста.

Это может звучать раздражающе неопределённо, но знаете, что? Большинство явлений природы заканчиваются неизвестно чем!

Как думаете, бактерия действительно планирует делиться каждые 14 часов? Нет, она просто питается забытым вами в холодильнике хлебом и растёт так быстро, как только может. Чтобы предсказать поведение этой бактерии, мы можем лишь использовать значения темпа её роста и длительности роста — и только потом мы получим конечное значение.

Иными словами, степень числа — это такой способ сказать «Начинаем с таких условий, изменяем их и смотрим, к чему мы придём». Этим и занимается наш Экспандотрон.

Идём к пониманию дробных степеней

Может ли Экспандотрон помочь нам осознать степени ещё глубже? Ну, к примеру, что означает 2 1,5 ?

Очень легко запутаться, если мы думаем о двойке в полуторной степени привычным способом — как о многократном умножении. Но в Экспандотроне всё просто: 1,5 — это всего лишь проведённое в нём время.

2 1 — это одна секунда в машине (двукратный рост)
2 2 — это две секунды в машине (четырёхкратный рост)

2 1,5 означает 1,5 секунды в машине, значит, этот рост окажется где-то между двукратным и четырёхкратным.

Умножение степеней

Что если мы захотим прогнать два цикла роста один за другим? Ну, например, мы используем машину в течение 2 секунд, а потом ещё 3 секунды на той же мощности:

Представьте самую обычную микроволновку. Разве это не будет самый обычный цикл длительностью в 5 секунд? Будет. Здесь происходит то же самое — раз уже мощность (основание) остаётся одинаковой, мы просто складываем время:

Квадратные корни

Продолжим. Предположим, мы выбрали мощность а и устанавливаем рост в течение 3 секунд:

Неплохо. Как будет выглядеть рост в течение половины этого времени? Логично, что 1,5 секунды.

А если мы проделаем то же самое два раза?

частичный рост * частичный рост = полный рост

Смотрим на это уравнение и видим, что «частичный рост» — это квадратный корень из значения полного роста. А если мы разделим время на три части?

частичный рост * частичный рост * частичный рост = полный рост

А вот и кубический корень! Это даёт нам интуитивное понимание того, почему деление степеней даёт нам корни: мы разбиваем время на равные доли.

Отрицательные степени

А как быть с отрицательными степенями? Отрицательные степени для нас будут значить обратный отсчёт во времени. Если движение вперёд во времени приводит нас к росту, движение назад, скорее всего, выльется в уменьшение числа.

Это значит следующее: «Секунду назад у нас была половина от текущего количества (1/2 1 ). Любой график экспоненциального роста строится именно так.

Выберите точку на шкале времени, например, 3,5 секунды (2 3,5 = 11,3). Через секунду мы удвоим наше количество (2 4,5 = 22,5). А секунду назад у нас была всего лишь половина от текущего количества (2 2,5 = 5,65).

Приходим к нулевой степени

Теперь самое интересное: что означает 3 0 ? А всё очень просто. Мы устанавливаем нашу микроволновку на мощность х3 и используем её в течение. 0 секунд. Это значит, что мы её просто не запускаем!

Значит, масштабирующий множитель равен единице, значит, никаких изменений с нашим числом не происходит. Новое число будет равняться исходному числу, то есть (вы же помните, что исходное число у нас единица?) единице. Масштабирования не происходит.

Приходим к нулевому основанию

А что мы делаем с 0 x ? Что ж, наша мощность в этом случае будет х0, а значит, после секунды времени Экспандотрон превращает число в ноль. Раз мы уже аннулировали число, совершенно неважно, сколько времени оно пробудет в машине — оно так и останется нулём.

Приходим к нулевому основанию в нулевой степени

Вот он, великий и ужасный 0 0 . И снова нас спасает Экспандотрон.

0 в степени 0 означает рост х0 в течение 0 секунд. Хоть мы и планировали аннулировать число, мы так и не запустили машину. Новое число равно исходному числу (то есть в наш Экспандотрон мы положили единицу), масштабирующий множитель тоже равен единице.

Конечно, Экспандотрона на самом деле не существует (а жаль!). Конечно, числа на самом деле не выстраиваются в линейку — они всего лишь один из множества способов взглянуть на мир.

Что даёт нам Экспандотрон? Он помогает нам не запинаться о кажущиеся препятствия вроде 2 1,5 или 0 0 . Как только мы начинаем понимать основные принципы роста, постепенно мы начнём дружить и с формулой Эйлера.

По материалам очаровательной статьи на Better Explained.