Уравнение Бернулли физический и геометрический смысл, вывод формулы Бернулли общего вида для идеальной жидкости, для потока реальной жидкости, для идеального газа

Уравнение Бернулли

Уравнение Бернулли для струйки жидкости формулируется следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия, т.е. сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии – есть величина постоянная во всех сечениях струйки.

Уравнение Бернулли выглядит так:

Подробное описание всех входящих в состав уравнения параметров уже описан в этой статье.

Содержание статьи

Смысл уравнения Бернулли

По существу вывода уравнение Бернулли для струйки идеальной жидкости представляет собой закон сохранения механической энергии, составленный применительно к единице массового расхода жидкости. Это следует из того, что в процессе вывода значения работы сил, приложенных к выделенному объему струйки и значения кинетической энергии этого объема были поделены на величину ρqΔT.

Отсюда вытекает, что поскольку член υ 2 /2 является мерой кинетической энергии единицы массы движущейся жидкости, то сумма членов gz+p/ρ будет мерилом ее потенциальной энергии.

В отношении величины gz это очевидно, ведь если частица жидкости массы m расположена на высоте z относительно некоторой плоскости и находится под действием сил тяжести, то способность ее совершить работу, т.е. её потенциальная энергия относительно этой плоскости равняется mgz. Но если её поделить на массу частиц m, то эта часть потенциальной энергии даст величину gz.

Для более ясного физического представления о том, что потенциальная энергия измеряется величиной p/ρ рассмотрим такую схему: пусть к трубе, заполненной жидкостью с избыточным давлением p, присоединен пьезометр, снабженный на входе в него краном.

Кран сначала закрыт, т.е. пьезометр свободен от жидкости, а элементарный объем жидкости ΔV массой ρ*ΔV перед краном находится под давлением p.

Если затем открыть кран, то жидкость в пьезометре поднимется на некоторую высоту, равную

Таким образом, единица массы, находящейся под давлением p, как бы несет в себе ещё заряд потенциальной энергии, определяемой величиной p/ρ.

В гидравлике для характеристики удельной энергии обычно используется понятие напор, под которым понимают энергию жидкости, отнесенную к единице силы тяжести, а не её массы. В соответствии с этим уравнение Бернулли записанное в начале этой статьи примет вид

Такое уравнение Бернулли для элементарной струйки идеальной жидкости в другой форме, весьма удобно для гидравлических расчетов и может быть сформулировано следующим образом.

Для элементарной струйки идеальной жидкости полный напор, т.е. сумма геометрического, пьезометрического и скоростного напоров, есть величина постоянная во всех её сечениях.

Отсюда следует, что между напором и удельной энергией существует очень простая зависимость

где э – удельная энергия

Уравнение Бернулли для элементарной струйки реальной жидкости

Если вместо идеальной жидкости рассматривать жидкость реальную, то уравнение Бернулли для реальной жидкости должно принять несколько другой вид.

При движении идеальной жидкости её полная удельная энергия или напор сохраняет постоянное значение по длине струйки, а при движении реальной жидкости эта энергия будет убывать по направлению движения. Причиной этого являются затраты энергии на преодоление сопротивлений движению, обусловленные внутренним трением в вязкой жидкости.

Если же мы рассмотрим два сечения для струйки идеальной жидкости: 1-1 в начале и 2-2 в конце струйки, то полная удельная энергия будет

Полная удельная энергия для сечения 1-1 всегда будет больше, чем полная удельная энергия для сечения 2-2 на некоторую величину потерь, и уравнение Бернулли в этом случае получается

Величина Э_1-2 представляет собой меру энергии, потерянную единицей массы жидкости на преодоление сопротивлений при её движениями между указанными сечениями.

Соответствующий этой потере удельной энергии напор называют потерей напора между сечениями 1-1 и 2-2 и обозначают h_1-2 . Поэтому уравнение Бернулли для элементарной струйки реальной жидкости можно представить в виде

Уравнение Бернулли для потока реальной жидкости

Уравнение Бернулли для струйки реальной жидкости это еще только половина дела, ведь в при решении различных практических вопросов о движении жидкостей приходится иметь дело с потоками конечных размеров. Уравнение Бернулли в этом случае может быть получено, исходя из рассмотрения потока как совокупности множества элементарных струек.

Учитывая, что все струйки движутся с одной и той же средней скоростью форма записи уравнения Бернулли для потока идеальной жидкости становится идентичной его записи для элементарной струйки.

В таком виде уравнение Бернулли обычно и применяется при решении практических задач для потоков однородной несжимаемой жидкости при установившемся движении, происходящем под действием одной силы тяжести.

Такое уравнение составляется для различных живых сечений потока, вблизи которых движение жидкости должно удовлетворять условиям медленно изменяющегося движения, хотя на пути между этими сечениями движение может и не удовлетворять указанным условиям.

Слагаемое h_1-2 в этом уравнении показывает потери напора на преодоление сопротивлений движению жидкости. При этом в гидравлике различают два основных вида сопротивлений:
– h_лп – линейные потери – сопротивления, проявляющиеся по всей длине потока, обусловленные силами трения частиц жидкости друг о друга и о стенки, ограничивающие поток.
– h_мп – местные потери – местные сопротивления, обусловленные различного рода препятствиями, устанавливаемыми в потоке (задвижка, кран, колено), приводящими к изменениям величины или направления скорости течения жидкости

Поэтому полная потеря напора между двумя сечениями потока при наличии сопротивлений обоих видов будет

Видео по теме

Уравнение Бернулли подходит и для газов. Явление уменьшения давления при повышении скорости потока является основой работы различных приборов для измерения расхода. Закон Бернулли справедлив и для жидкостей вязкость которых равна нулю. При описании течения таких жидкостей используют уравнение Бернулли с добавлением слагаемых учитывающих потери на местные сопротивления.

Течение жидкости и уравнение Бернулли для новичков

• 12 января 2021 г.
• 6 минут
• 54 402

Как закон Всемирного Тяготения Ньютона действовал задолго до самого Ньютона, так и уравнение Бернулли существовало задолго до того, как родился сам Бернулли. Ему удалось лишь облечь это уравнение в наглядную форму, в чем его неоспоримая и огромная заслуга. Зачем мне уравнение Бернулли, спросите Вы, ведь я прекрасно жил и без него. Да, но оно может пригодиться Вам хотя бы на экзамене по гидравлике! Как говорится, «все не так уж плохо, если ты знаешь и можешь сформулировать уравнение Бернулли».

Кто такой Бернулли?

Даниил Бернулли – сын известного ученого Якоба Бернулли, швейцарский математик и физик. Жил с 1700 по 1782 годы, а с 1725 по 1733 трудился в Петербургской Академии наук. Помимо физики и математики Бернулли также изучал медицину наряду с Д’Аламбером и Эйлером считается отцом основателем математической физики. Успехи этого человека позволяют с уверенностью сказать, что это был настоящий «супермозг».

Д. Бернулли (1700-1782)

Идеальная жидкость и течение идеальной жидкости

Помимо известной нам материальной точки и идеального газа существует также идеальная жидкость. Какой-нибудь студент, конечно, может подумать, что эта жидкость – его любимое пиво или кофе, без которого невозможно жить. Но нет, идеальная жидкость – это жидкость, которая абсолютно несжимаема, лишена вязкости и теплопроводности. Тем не менее, такая идеализация дает вполне хорошее описание движения реальных жидкостей в гидродинамике.

Течением жидкости называется движение ее слоев относительно друг друга или относительно всей жидкости.

Помимо того есть разные режимы течения жидкости. Нас интересует тот случай, когда скорость потока в какой-то конкретной точке не меняется со временем. Такой поток называют стационарным. При этом скорость течения в различных точках стационарного потока может различаться.

Поток жидкости– совокупность частиц движущейся жидкости.

Поток жидкости

Вывод уравнения Бернулли

Но как описать движение жидкости? Для этого нам нужно знать вектор скорости частиц, точнее зависимость его от времени. Совокупность скоростей в разных точках потока дает поле вектора скорости.

Рассмотрим стационарное течение жидкости по трубке. В одном месте сечение этой трубки равно S1, а в другой – S2. При стационарном потоке через оба сечения за одинаковый промежуток времени пройдет одинаковое количество жидкости.

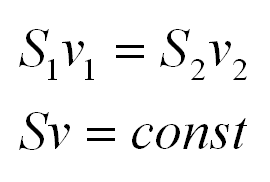
Данное уравнение – уравнение неразрывности струи.

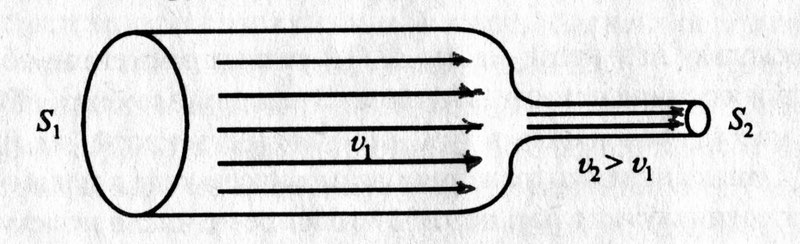К выводу уравнения Бернулли

Узнав его, Бернулли решил установить связь между давлением и скоростью жидкости в разных сечениях. Полное давление – это сумма статистического (обусловлено потенциальной энергией жидкости) и динамического давлений (обусловлено кинетической энергией). Оказывается, сумма статического и динамического давлений в любом сечении трубы постоянна. Само же уравнение Бернулли имеет вид:

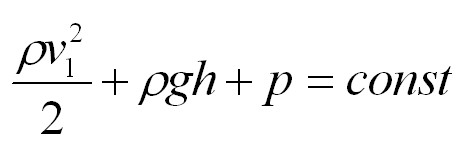
Смысл уравнения Бернулли

Физический смысл уравнения Бернулли. Уравнение Бернулли является следствием закона сохранения энергии. Первый член уравнения Бернулли – это кинетическая энергия, второе слагаемое уравнения Бернулли – потенциальная энергия в поле силы тяжести, третье – работа силы давления при подъеме жидкости на высоту h.

Вот и все, друзья, не так уж и страшно. Совсем немного времени, а Вы уже знаете уравнение Бернулли. Даже если Вы не знаете больше ничего, с этими знаниями идти на экзамен или зачет гораздо лучше, чем просто так. А если Вам необходима помощь в том, как решать задачи на уравнение Бернулли – не стесняйтесь и оформляйте заявку. После того как наши авторы распишут решение уравнения Бернулли максимально подробно, у Вас не останется пробелов в знаниях.

Уравнение Бернулли

Основные уравнения гидродинамики – уравнение Бернулли и неразрывности позволяют установить взаимосвязь между параметрами плавно изменяющегося потока.

Уравнение Бернулли для потока идеальной жидкости

Рассмотрим установившееся движение потока идеальной несжимаемой жидкости, на которую действует только одна массовая сила – сила тяжести.

Выбреем два живых сечения , 1-1 в начале рассматриваемого участка, 2-2 – в конце.

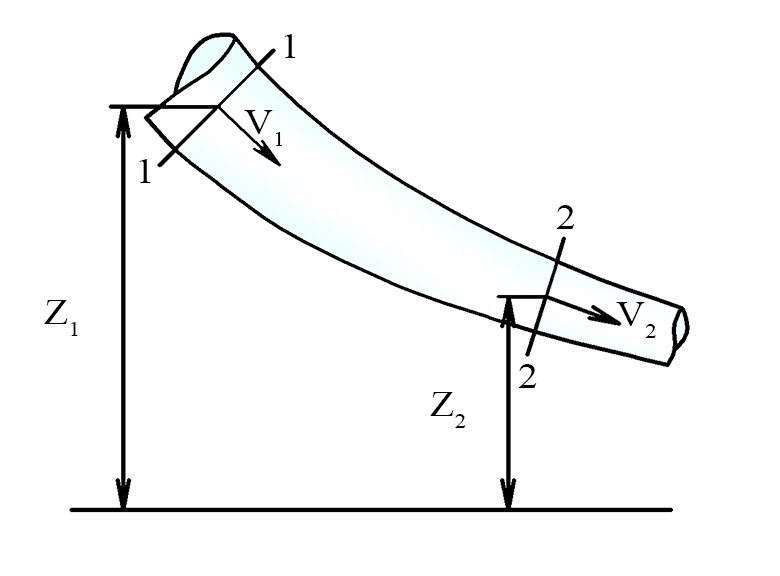
Запишем для этого случая уравнение, связывающее между собой скорость движения жидкости и ее давление в каждом сечении.

Указанное уравнение называют законом или уравнением Бернулли для элементарной струйки идеальной несжимаемой жидкости.

Для каждого рассматриваемого сечения полный напор есть сумма геометрического, пьезометрического и скоростного напора. Для идеальной жидкости (т.е. при отсутствии потерь энергии) полный напор – величина постоянная.

Уравнение Бернулли можно записать и в другом виде, умножим обе части уравнения на g получим:

Физический смысл уравнения Бернулли

Составляющие уравнения Бернулли являются различными формами удельной (отнесенной к единице массы) механической энергии жидкости:

• gz – удельная энергия положения,
• p/ρ – удельная энергия давления движущейся жидкости,
• V₁ 2 /2 – удельная кинетическая энергия жидкости,
• gz + p/ρ + V 2 /2 = Hg – полная удельная энергия движущейся идеальной жидкости.

Физический и энергетический смысл уравнения Бернулли заключается в постоянстве полной удельной энергии вдоль элементарной струйки идеальной жидкости.

Уравнение Бернулли отражает закон сохранения механической энергии для идеальной несжимаемой жидкости.

Уравнение Бернулли для потока реальной вязкой жидкости

Если на участке между расчетными сечениями не совершается механическая работа, а движение является установившимся, без притока и отбора жидкости, и сама жидкость является несжимаемой, то для потока будут справедливы зависимости:

Н₁=Н₂ + Δh_{1 – 2} z₁ + p₁/ρg + V₁ 2 /2g = z₂ + p₂/ρg + V₂ 2 /2g + Δh_{1 – 2}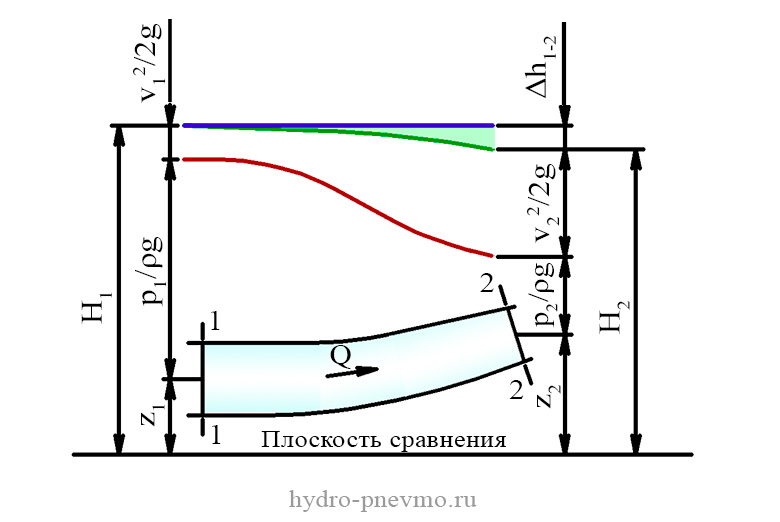

Уравнение Бернулли устанавливает связь между полными напорами потока жидкости на участке ограниченными сечениями 1-1 и 2-2. В соответствии с уравнением Бернулли полный напор потока Hi уменьшается от сечения 1-1 к сечению 2-2 на величину потерь напора (энергии) h_{1 – 2}, вызванных гидравлическими сопротивлениями участка.

Иллюстрация уравнения Бернулли

Для иллюстрации закона Бернулли на координатной плоскости, совмещенной с принципиальной гидравлической схемой системы изображают напорную и пьезометрическую линии.

Уравнение Бернулли для горизонтальной трубы

Для горизонтальных трубопроводов и силовых гидроприоводов, в которых пьезометрический набор существенно превышает геометрический удобна следующая форма записи уравнения Бернулли:

Алгоритм решения задач с помощью уравнения Бернулли

Задачи с помощью уровнения Бернулли удобно решать в следующей последовательности:

1. Изобразить принципиальную гидравлическую схему системы
2. Провести общую для всего потока плоскость сравнения. Лучше всего провести ее самой нижней точки системы, например на уровне оси самого нижнего трубопровода, или не уровне жилкости самого нижнего резервуара.
3. Выбрать два (или несколько) живых сечения. Одно сечение выбирается в, том месте где параметры потока известны, другое там, где нужно определить неизвестные параметры (напрмер давление). Сечения следует выбирать только в тех местах где движение можно считать плавно изменяющимся. Нумеровать сечения следует в направлении движения жидкости.
4. Записать уравенение Бернулли для выбранных сечений.
5. При необходимости определить гидравлические потери напора на различных участка гидросистемы.
6. Вычислить неизвестные параметры, используя уранение Бренулли.

Лекция 4

4.1. Уравнение Бернулли для жидкости

Рассмотрим поток жидкости, проходящий по трубопроводу переменно­го сечения (рис. 10). В первом сечении гидродинамический напор пусть ра­вен H1. По ходу движения потока часть напора H1 необратимо потеря­ется из-за проявления сил внутреннего трения жидкости и во втором сечении напор уменьшится до H2 на величину потерь напора H.

Уравнение Бeрнýлли для жидкости в самом простейшем виде записывается так:

H1 = H2 + H ,

то есть это уравнение для двух сечений потока в направлении его течения, выраженное через гидродинамические напоры и отражающее закон сохра­нения энергии (часть энергии переходит в потери) при движении жидкости.

Уравнение Бeрнýлли в традиционной записи получим, если в по­следнем ра­венстве раскроем значения гидродинамических напоров H1 и H2 (м) :

.

Энергетический смысл уравнения Бeрнулли заключается в том, что оно отражает закон сохранения энергии: сумма потенциальной z+hp, кинетической v2/2g энергии и энергии потерь H остаётся неизменной во всех точках потока.

4.2. Геометрическая интерпретация уравнения Бернулли

Положение любой частицы жидкости относительно некоторой произвольной линии нулевого уровня 0-0 определяется вертикальной координатой Z. Для реальных гидравлических систем это может быть уровень, ниже которого жидкость из данной гидросистемы вытечь не может. Например, уровень пола цеха для станка или уровень подвала дома для домашнего водопровода.

· Как и в гидростатике, величину Z называют нивелирной высотой.

· Второе слагаемое – носит название пьезометрическая высота. Эта величина соответствует высоте, на которую поднимется жидкость в пьезометре, если его установить в рассматриваемом сечении, под действием давления P.

· Сумма первых двух членов уравнения ¾ гидростатический напор.

· Третье слагаемое в уравнения Бернулли называется скоростной высотой или скоростным напором. Данную величину можно представить как высоту, на которую поднимется жидкость, начавшая двигаться вертикально со скорость u при отсутствии сопротивления движению.

· Сумму всех трёх членов (высот) называют гидродинамическим или полным напором и, как уже было сказано, обозначают буквой Н.

Все слагаемые уравнения Бернулли имеют размерность длины и их можно изобразить графически.

4.3. Энергетическая интерпретация уравнения Бернулли

Выше было получено уравнение Бернулли с использованием энергетических характеристик жидкости. Суммарной энергетической характеристикой жидкости является её гидродинамический напор.

С физической точки зрения это отношение величины механической энергии к величине веса жидкости, которая этой энергией обладает. Таким образом, гидродинамический напор нужно понимать как энергию единицы веса жидкости. И для идеальной жидкости эта величина постоянна по длине. Таким образом, физический смысл уравнения Бернулли это закон сохранения энергии для движущейся жидкости.

.

Физический смысл слагаемых, входящих в уравнение следующий:

· Z – потенциальная энергия единицы веса жидкости (удельная энергия) – энергия, обусловленная положением (высотой) единицы веса жидкости относительно плоскости сравнения (нулевого уровня), принимаемой за начало отсчета;

· – потенциальная энергия единицы веса жидкости – энергия, обусловленная степенью сжатия единицы веса жидкости, находящейся под давлением ;

· – полная потенциальная энергия единицы веса жидкости;

· – кинетическая энергия единицы веса жидкости – энергия, обусловленная движением единицы веса жидкости со скоростью u;

· H – полная энергия единицы веса жидкости (полная удельная энергия).

4.4. Уравнение Бернулли для потока реальной жидкости

В реальных потоках жидкости присутствуют силы вязкого трения. В результате слои жидкости трутся друг об друга в процессе движения. На это трение затрачивается часть энергии потока. По этой причине в процессе движения неизбежны потери энергии. Эта энергия, как и при любом трении, преобразуется в тепловую энергию. Из-за этих потерь энергия потока жидкости по длине потока, и в его направлении постоянно уменьшается. Т. е. напор потока Hпотока в направлении движения потока становится меньше. Если рассмотреть два соседних сечения 1-1 и 2-2, то потери гидродинамического напора Δh составят:

,

где H1-1– напор в первом сечении потока жидкости,

H2-2 – напор во втором сечении потока,

∆h – потерянный напор – энергия, потерянная каждой единицей веса движущейся жидкости на преодоление сопротивлений на пути потока от сечения 1-1 до сечения 2-2.

С учётом потерь энергии уравнение Бернулли для потока реальной жидкости будет выглядеть

Индексами 1 и 2 обозначены характеристики потока в сечениях 1-1 и 2-2.

Если учесть, что характеристики потока V и α зависят от геометрии потока, которая для напорных потоков определяется геометрией трубопровода, понятно, что потери энергии (напора) в разных трубопроводах будут изменяться неодинаково. Показателем изменения напора потока является гидравлический уклон I, который характеризует потери напора на единице длины потока. Физический смысл гидравлического уклона – интенсивность рассеяния энергии по длине потока. Другими словами, величина I показывает, как быстро трубопровод поглощает энергию потока, протекающего в нём

.

Изменение энергии по длине потока удобно проследить на графиках. Из уравнения Бернулли для потока реальной жидкости (закона сохранения энергии) видно, что гидродинамическая линия для потока реальной жидкости (с одним источником энергии) всегда ниспадающая. То же справедливо и для пьезометрической линии, но только в случае равномерного движения, когда скоростной напор а уменьшение напора происходит только за счёт изменения потенциальной энергии потока, главным образом за счёт уменьшения давления P.

4.5. Разность напоров и потери напора

Различие в применении терминов «разность напоров» и «потери напора» с одним и тем же обозначениемH поясним на примерах.

Движение жидкости происходит только при наличии разности на­поров (H = H1 – H2), от точки с бóльшим напором H1 к точке с ме­ньшим H2. Например, если два бака, заполненных водой до разных вы­сотных отметок, соединить трубопроводом, то по нему начнётся пере­текание в бак с меньшей от­меткой уровня воды под влиянием разности напоров H, равной в этом случае разности отметок уровней воды в ба­ках. При выравнивании уровней напоры в обоих баках становятся оди­наковыми H1 = H2 , разность напоров H=0 и перетекание пре­кращается.

Потери напора H отражают потерю полной энергии потока при движении жидкости. Если в предыдущем примере на трубе установить задвижку и закрыть её, то движение воды прекратится и потерь напора не будет (H = = 0), однако разность уровней воды будет создавать неко­торую разность напоров H. После открывания задвижки вода вновь начнёт перетекать по трубе и общие потери напора в трубопроводе при движении из одного бака в другой будут равны разности напоров в баках H = H1 – H2 , то есть мы опять пришли к уравнению Бернулли.

Таким образом, «разность напоров» является причиной движения воды, а «потеря напора» — следствием. При установившемся движении жидкости они равны. Измеряются они в одних и тех же единицах СИ: метрах по высоте.

Обычно в гидравлических задачах при известных v или q опреде­ляемая величина H назывется потерей напора и, наоборот, при оп­ределении v или q известная H — разностью напоров.

4.6. Связь давления и скорости в потоке

Связь давления и скорости в потоке жидкости — обратная: если в каком-то месте потока скорость увеличивается, то давление здесь малó, и, наоборот, там, где скорости невелики, давление повышенное. Эту законо­мерность объясним на основе уравнения Бернýлли.

Рассмотрим работу водоструйного насоса (см. рис. 11). На подходе по на­гнетательному трубопроводу 1 поток рабочей жидкости имеет относи­те­ль­но небольшую скорость v1 и высокое избыточное давление pизб1. Проходя через соплó 2, поток сужается, скорость его резко возрастает до v2. Для дальнейших рассуждений запишем уравнение Бернýлли так:

.

Здесь нет z1 и z2, так как труба горизонтальная, а величиной потерь на­пора DH» пренебрегаем. Так как в правой части уравнения кинети­ческая составляющая энергии потока резко возросла из-за увеличения v2, то потенциальная составляющая, связанная с избыточным давлением после соплá pизб2, наоборот, уменьшится. Величину pизб2 можно выразить из этого уравнения и найти численное значение. Если pизб2 получается отри­цательным, то, значит, возник вакуум (полное давление в струе стало меньше атмосферного). В последнем случае пьезометрическая линия опу­стится ниже отметки самой струи (см. рис 11).

Таким образом в струе рабочей жидкости после соплá образуется об­ласть пониженного давления или даже вакуум, что вызывает подсос транс­портируемой жид­кости по всасывающему трубопроводу 3 (см. рис. 11). Далее обе жидкости смешиваются в горловине 4 и транспортируются по отво­дяще­му трубопро­воду 5.

Водоструйные насосы не имеют трущихся частей, в этом их пре­имущес­тво перед механическими. По их принципу работают также эжекто­ры, гидро­эле­ваторы, насосы для создания вакуума.

Уравнение Бернулли физический и геометрический смысл, вывод формулы Бернулли общего вида для идеальной жидкости, для потока реальной жидкости, для идеального газа

Е. М. Пантелова

В. А. Кисюк

О. С. Копылова

М. И. Кузин

ФГБОУ ВО Ставропольский государственный аграрный университет

Россия, г. Ставрополь

Аннотация: в данной статье мы рассмотрим применение уравнения Бернулли в гидродинамики, подробно рассмотрим вывод уравнения Бернулли для потока идеальной жидкости и для потока реальной жидкости.

Основным уравнением гидродинамики считается полученное в 1738 году уравнение Даниила Бернулли. Данное выражение демонстрирует закон сохранения энергии движущейся жидкости и создает взаимосвязь между средней скоростью υ, давлением P, и пьезометрической высотой z в разных сечениях потока. Многие задачи решаются с помощью этого уравнения.

Ключевые слова: уравнение Бернулли, жидкость, сечение, трубка Пито, энергия.

Рассмотрим трубопровод изменчивого диаметра, который расположен в пространстве под углом β (рис.1).

На данном участке трубопровода подберем произвольно два сечения: сечение 1-1 и сечение 2-2. От первого сечения ко второму ввысь по трубопроводу перемещается жидкость, расход которой равен Q.

Для того, что бы измерить давление жидкости применяются пьезометры – стеклянные трубки с тонкими стенками, в таких трубках жидкость поднимается на высоту .Уровень жидкости в пьезометрах, установленных в каждом из сечений, поднимается на разную высоту.

Рис.1 к выводу уравнения Бернулли для идеальной жидкости

Так же в сечениях 1-1 и 2-2 установлена трубка с загнутым концом. Этот конец направлен навстречу потоку жидкости. Эти трубки получили название трубки Пито. Если мы будем отсчитывать от пьезометрической линии, то жидкость в таких трубках поднимется на разные уровни. Построим пьезометрический отрезок следующим способом: если между заданными сечениями поставить пару подобных пьезометров и провести в них кривую через показания уровней жидкости, то мы получим зигзагообразную линию (рис.1).

Относительно произвольной прямой 0-0, проходящей горизонтально, высота уровней в трубках Пито остается постоянной. Эту прямую назовем плоскостью сечения.

Уровень полной энергии трубопровода показывает горизонтальная линия, которая проведена, через показания уровней жидкости в трубках Пито.

Для сечений 1-1 и 2-2 потока идеальной жидкости уравнение Бернулли запишем в виде:

Так как два сечения подобранны произвольно, то полученное уравнение запишем иначе:

Данное уравнение можно прочесть следующим образом: сумма трех членов уравнения Бернулли для любого сечения потока идеальной жидкости есть величина постоянная. Если рассматривать это уравнение с энергетической точки зрения, то каждый член представляет собой некоторый вид энергии:

z1 и z2 – удельные энергии положения, характеризующие потенциальную энергию в сечениях 1-1 и 2-2;

и – удельные энергии давления, характеризующие потенциальную энергию давления в тех же сечениях;

и – удельные кинетические энергии в тех же сечениях.

Таким образом, опираясь на уравнение Бернулли, мы получим, что в любом сечении полная удельная энергия идеальной жидкости остается постоянной.

Уравнение Бернулли можно объяснить геометрически. Дело в том, что каждый член уравнения имеет линейную размерность. Смотря на рис.1 заметим, что z₁ и z₂ – геометрические высоты сечений 1-1 и 2-2 над плоскостью сравнения; и – пьезометрические высоты; и – скоростные высоты в указанных сечениях [1-6].

В данном случае уравнение Бернулли можно прочитать так: сумма геометрической, пьезометрической и скоростной высоты для идеальной жидкости есть величина постоянная.

Уравнение Бернулли для потока реальной жидкости и для потока идеальной жидкости немного различны, так как при движении реальной жидкости возникают силы трения, и что бы преодолеть эти силы жидкость тратит энергию. В результате полная удельная энергия жидкости в сечении 2-2 окажется меньше, чем в сечении 1-1, на величину потерянной энергии (рис.2)

Рис.2 к выводу уравнения Бернулли для реальной жидкости

Обозначим потерянную энергию (потерянный напор) за (имеет линейную размерность).

Запишем уравнение Бернулли для реальной жидкости в виде:

Из второго рисунка мы видим, что по мере того, как жидкость движется от первого сечения ко второму потерянный напор (выделен штриховкой) во время всего пути увеличивается. В итоге, уровень первоначальной энергии, которой обладает жидкость в первом сечении, для второго сечения будет складываться из четырех составляющих: геометрической высоты, пьезометрической высоты, скоростной высоты и потерянного напора между двумя сечениями [7-10].

Коэффициенты и , которые зависят от режима течения жидкости, для ламинарного режима , а для турбулентного режима , называются коэффициентами Кориолиса. Потерянная высота складывается из линейных потерь, вызванных силой трения между слоями жидкости, и потерь, вызванных местными сопротивлениями (изменениями конфигурации потока)

Рассмотрим пример решения задачи с помощью уравнения Бернулли.

В дождевальной установке вода подается сначала по трубе диаметром h ₂ =40 мм, которая сужается до h ₁ =24 мм. Статическое давление в широкой части трубы равно 250 кПа, скорость равна 14,4 м/с. Определить статическое давление в узкой части трубы. Плотность воды 10 3 кг/м 3 .

Запишем уравнение неразрывности:

;

Получим, что скорость в узкой части трубки будет равна:

Уравнение Бернулли в данной задаче будет иметь вид:

Из этого уравнения выразим статическое давление в узкой части трубы:

Теперь найдем значение этого давления:

Мы получили, что статическое давление в узкой части дождевальной установке равна .

Большая часть задач практической гидродинамики решается с помощью уравнения Бернулли. Для этого выбирают два сечения по длине потока жидкости, таким образом, чтобы для одного из них были известны величины: Р, ρ, g , а для другого сечения одна или две величины подлежали определению. При двух неизвестных для второго сечения используют уравнение постоянства расхода жидкости, которое имеет вид: υ₁ω ₁ = υ₂ω₂.

4. Герасимов Е.В., Кисюк В.А., Овсянников С.А. Перспективы утилизации тепловых потерь двигателя // В сборнике: Актуальные проблемы научно-технического прогресса в АПК VII Международная научно-практическая конференция в рамках XIX Международной агропромышленной выставки “Агроуниверсал – 2013”. / Ставрополь. – 2013. – С. 69-73.

5. Герасимов Е.В., Кисюк В.А., Алексеенко В.А., Сидельников Д.А. Определение режимных и конструктивных параметров работы обезвоживающего устройства // В сборнике: Актуальные проблемы научно-технического прогресса в АПК Сборник научных статей XII Международной научно-практической конференции, в рамках XVIII Международной агропромышленной выставки “Агроуниверсал – 2016”. / Ставрополь. – 2016. – С. 273-277.

6. Любая С.И., Стародубцева Г.П., Афанасьев М.А., Копылова О.С. Практикум для лабораторных работ по физике – Ставрополь, 2015.

Сведения об авторе:

Пантелова Елизавета Михайловна – студентка 2 курса электроэнергетического факультета СтГАУ

Кисюк Василий Адамович – к. с. х. н., доцент кафедры физики СтГАУ

Копылова Оксана Сергеевна – к. ф. м. н., доцент кафедры физики СтГАУ

Кузин Михаил Игоревич – студент 4 курса электроэнергетического факультета СтГАУ

E. M. Pantelova

O. S. Kopylova

V. A. Kisuk

M. I. Kuzin

BERNOULLI’S EQUATION FOR IDEAL FLUID

Summary: in this article we will discuss the application of Bernoulli’s equation in fluid dynamics, a detailed look at the output of the Bernoulli’s equation for fluid flow and for the flow of a real fluid.

The basic equation of hydrodynamics is deemed to be received in 1738 Daniel Bernoulli equation. This expression demonstrates the law of conservation of energy of a moving fluid and creates a relationship between the average velocity υ, the pressure P, and the piezometric elevation z in the different sections of the stream. Many problems are solved using this equation.

Keywords: Bernoulli’s equation, liquid, section, Pitot’s tube, energy.

1. Afanasyeva V. S., Kopylova O. S., Afanasiev M. A., Kopylov V. B. Design of physics lessons in 8th grade on the topic: “Changing aggregate States of substances” taking into account GEF // Naukar. – 2014. – № 5 (25). – Pp. 2-9.

2. Afanasyev M. A., Gutsevich, A., Kisuk V. A., Hytov, K.-M. V., Yakuba, I. V. Design of the laboratory work on hydrostatic pressure // In book: Physical-technical problems of creation of new technologies in agroindustrial complex / Stavropol. – 2015. – S. 11-15.

3. Vecher O. V., Khashchenko A. A., Vorob’ev I. N., Afanasyev M. A., Theoretical analysis of rate of evaporation of liquid from the surface of section of two liquid phases // In the book: the Use of modern resource-saving innovative technologies in agriculture III international scientific-practical conference. / Stavropol. – 2013. – P. 29-31.

4. Gerasimov E. V., Kisuk V. A., Ovsyannikov S. A. Prospects of the use of thermal losses of the motor // In collection: Actual problems of scientific-technical progress in agriculture VII international scientific-practical conference in the framework of the XIX International agricultural exhibition “Agrouniversal – 2013”. / Stavropol. – 2013. – P. 69-73.

5. Gerasimov E. V., Kisuk V. A., Alekseenko V. A., Sidelnikov D. A. Definition of operating and design parameters of the dewatering device // In collection: Actual problems of scientific-technical progress in agriculture the Collection of scientific articles of the XII International scientific-practical conference in the framework of the XVIII International agricultural exhibition “Agrouniversal – 2016”. / Stavropol. – 2016. – Pp. 273-277.

6. Lybaya S. I., Starodubtseva G. P., Afanasyev M. A., Kopylova O. S. Practicum for laboratory works on physics – Stavropol, 2015.

7. Menshikov V. A., Khashchenko A. A., Afanasyev M. A. General description of the process of boiling liquid and its application in modern power system // proceedings: New technologies in agriculture and food industry with the use of electro-physical factors and ozone VII all-Russian scientific-practical conference. / Stavropol. – 2012. – P. 113-115.

8. Khainovskii V. I., Gorokhov A.V., Afanasyev M. A. Methods and accuracy of measurement of surface tension of liquids // In the book: Physical and technical problems of creation of new technologies in agriculture III Russian scientific-practical conference. / Stavropol. – 2005. – S. 227-232.

9. Khashchenko A. A., Menshikov A. V., Afanasyev M. A., Vorob’ev I. N. Experimental study of the value of a superheated layer of liquid at boiling // In the book: New technologies in agriculture and food industry with the use of electro-physical factors and ozone VII all-Russian scientific-practical conference. / Stavropol. – 2012. – S. 111-112.

10. Khashchenko A. A., Menshikov A. V., Afanasyev M. A., Pulia A. V., Korobov Y. A. Experimental study of the processes of evaporation and boiling of liquids // proceedings: New technologies in agriculture and food industry with the use of electro-physical factors and ozone VII all-Russian scientific-practical conference. / Stavropol. – 2012. – P. 108-111.

7. Уравнение Бернелли для идеальной и реальной жидкостей.

Уравнение Бернулли для струйки идеальной жидкости. движение жидкости в трубопроводах и каналах осуществляется за счет энергии самой жидкости . чаще всего необходимо энергии для перемещения передавай передается жидкости с помощью насосов.

Механическая энергия жидкости состоит из трех видов энергии: энергии положение, давления и кинетической энергии . В гидравлике под напором понимает энергию жидкости относительно единица веса. в этом случае напор измеряется в метрах что используется при его графическом представлении. Полный гидродинамический напор действующей жидкости равен сумме3 напоров геометрического напора( Удельная потенциальная энергия положения) , пьезометрического напора (Удельная потенциальная энергия давления) и скоростного напора Удельная кинетическая энергия).

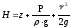
Уравнение Бернулли для потока идеальной жидкости

В потоке идеальной жидкости, движущийся по трубопроводам и каналам, вследствие отсутствия потери энергии при движении, полный гидродинамический напор жидкости остается постоянным. это условие является частным случаем законы сохранения энергии и записывается для двух сечений потока жидкости равенство полное гидростатический напор от называют уравнением Бернул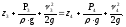ли или

в процессе движения идеальной жидкости один вид энергии может превращаться в другой , Однако полная энергия при этом остается без изменений.

Уравнение Бернулли для реальной жидкости

При движении реальной вязкой жидкости вследствие влияния сил молекулярного сцепления между стенкой и жидкостью происходит торможение потока приводящее к скольжению слоев жидкости друг относительно друга на вене и возникновению напряжений трения между слоями. Кроме того движения вязкой жидкости часто сопровождается вращением частиц , вихреобразованием и перемешиванием . Все это требует затрат энергии жидкости, поэтому энергия реальной жидкости не остается постоянной, как случается идеальной жидкостью, а постоянно расходуется на Преодоление сопротивлений и , следовательно уменьшается вдоль потока . Из-за неравномерного распределения скоростей потока реальной жидкости приходится вводить в рассмотрение среднюю скорость , а также средние значения Удельной энергии жидкости в данном сечении . при этом предполагается, что гидростатический напор в пределах сечения , есть величина одинакова для всех точек данного сечения.

В Результате полная Удельная энергия жидкости в течении 3-3 будет больше полной удельной энергии в сечении 4-4 на величину потерянной Удельной энергии . Потерянная удельная энергия или потерянный напор обозначаетсяи имеют также линейную размерность. уравнение Бернулли для реальной жидкости, таким образом представляет собой баланс энергии в потоке с учетом потерь.

8. Геометрический и физический смысл уравнения Бернулли.

Физический смысл

геометрический напор(z) характеризует запас удельной потенциальной энергии положения пьезометрический напор() характеризует запас энергии жидкости обусловленный ее давлением относительно давления сравнения (часто атмосферного давления . Удельная потенциальная энергия давления) геометрический и пьезометрический напоры присущи жидкости находящейся в покое, поэтому их сумму называют гидростатическим напором. скоростной напор( ) характеризует запас энергии обусловленный скоростью ее движения. (Удельная кинетическая энергия)

сумма трех наборов называется полный гидродинамический напор.

Геометрический смысл

геометрический напор равен расстоянию от плоскости сравнения до рассматриваемой точке жидкости (для потока жидкости до точки совпадающий с центром тяжести рассматриваем его сечения) пьезометрический напор это расстояние в пьезометрической трубке (To есть расстояние до рассматриваемой точки от плоскости).

Броуновское движение

Нам известно, что все вещества состоят из огромного числа очень и очень маленьких частиц, которые находятся в непрерывном и беспорядочном движении. Откуда нам это стало известно? Как учёные смогли узнать о существовании настолько маленьких частиц, которые ни в один оптический микроскоп невозможно увидеть? И уж тем более, как им удалось выяснить, что эти частицы находятся в непрерывном и беспорядочном движении? В этом учёным помогли разобраться два явления — броуновское движение и диффузия. Об этих явлениях мы и поговорим более подробно.

2. Броуновское движение

Английский учёный Роберт Броун не был физиком или химиком. Он был ботаником. И он совсем не ожидал, что откроет столь важное для физиков и химиков явление. И он не мог даже подозревать о том, что в своих довольно простых экспериментах он будет наблюдать результат хаотичного движения молекул. А это было именно так.

Что же это были за эксперименты? Они были почти такие же, что делают ученики на уроках биологии, когда с помощью микроскопа пытаются рассмотреть, например, клетки растений. Роберт Броун хотел рассмотреть в микроскоп пыльцу растений. Рассматривая зёрна пыльцы в капле воды, он заметил, что зёрна не находятся в покое, а непрерывно дёргаются, будто они живые. Наверное, сначала он так и подумал, но будучи учёным, конечно же отбросил эту мысль. Ему не удалось понять, почему эти зёрна пыльцы ведут себя таким странным образом, но он описал всё увиденное, и это описание попало в руки физиков, которые тут же поняли, что перед ними наглядное доказательство непрерывного и беспорядочного движения частиц.

Объясняется это движение, описанное Броуном, следующим образом: зёрна пыльцы достаточно велики, так что мы можем увидеть их в обычный микроскоп, а вот молекулы воды мы не видим, но, в то же время, зёрна пыльцы достаточно малы, чтобы из-за ударов по ним молекул воды, окружающих их со всех сторон, они смещались то в одну, то в другую сторону. То есть этот хаотичный «танец» зёрен пыльцы в капле воды показывал, что молекулы воды непрерывно и беспорядочно с разных сторон ударяют по зёрнам пыльцы и смещают их. С тех пор непрерывное и хаотичное движение мелких твёрдых частичек в жидкости или газе стали называть броуновским движением. Важнейшей особенностью этого движения является то, что оно непрерывное, то есть не прекращается никогда.

Диффузия — это ещё один пример наглядного доказательства непрерывного и беспорядочного движения молекул. И заключается оно в том, что газообразные вещества, жидкости и даже твёрдые вещества, хотя и намного медленнее, могут самоперемешиваться друг с другом. К примеру, запахи различных веществ распространяются в воздухе даже в отсутствие ветра именно благодаря этому самоперемешиванию. Или вот ещё пример — если в стакан с водой бросить несколько кристаллов марганцовки и, не перемешивая воду, подождать около суток, то мы увидим, что вся вода в стакане будет окрашена равномерно. Это происходит из-за непрерывного движения молекул, которые меняются местами, и вещества постепенно перемешиваются самостоятельно без внешнего воздействия.

4. Свойства броуновского движения и диффузии

Когда учёные-физики стали более подробно рассматривать явление, описанное Робертом Броуном, они заметили, что, как и диффузию, этот процесс можно ускорить, повышая температуру. То есть в горячей воде и окрашивание с помощью марганцовки будет происходить быстрее, и движение мелких твёрдых частичек, к примеру, графитовой крошки или тех же зёрен пыльцы, происходит с большей интенсивностью. Это подтверждало тот факт, что скорость хаотичного движения молекул напрямую зависит от температуры. Не вдаваясь в подробности, перечислим, от чего может зависеть и интенсивность броуновского движения, и скорость протекания диффузии:

1) от температуры;

2) от рода вещества, в котором эти процессы происходят;

3) от агрегатного состояния.

То есть при равной температуре диффузия газообразных веществ протекает значительно быстрее, чем жидкостей, не говоря уже о диффузии твёрдых тел, которая происходит настолько медленно, что её результат, и то очень незначительный, можно заметить или при очень высоких температурах, или за очень большое время — годы или даже десятилетия.

5. Практическое применение

Диффузия и без практического применения имеет огромное значение не только для человека, но и для всего живого на Земле: именно благодаря диффузии в нашу кровь через лёгкие попадает кислород, именно посредством диффузии растения добывают из почвы воду, поглощают углекислый газ из атмосферы и выделяют в ней кислород, а рыбы дышат в воде кислородом, который из атмосферы посредством диффузии попадает в воду.

Явление диффузии применяется и во многих областях техники, причём именно диффузии в твёрдых телах. К примеру, есть такой процесс — диффузионная сварка. В этом процессе детали очень сильно прижимаются друг к другу, нагреваются до 800 °C и посредством диффузии происходит их соединение друг с другом. Именно благодаря диффузии земная атмосфера, состоящая из большого количества различных газов, не разделяется на отдельные слои по составу, а везде примерно однородна — а ведь будь иначе, мы вряд ли смогли бы дышать.

Существует огромное количество примеров влияния диффузии на нашу жизнь и на всю природу, которые может найти любой из вас, если захочет. А вот о применении броуновского движения мало что можно сказать, кроме того, что сама теория, которая описывает это движение, может применяться и в других, казалось бы совершенно не связанных с физикой, явлениях. К примеру, эту теорию используют для описания случайных процессов, с применением большого количества данных и статистики — таких, как изменение цен. Теория броуновского движения используется для создания реалистичной компьютерной графики. Интересно, что человек, заблудившийся в лесу движется примерно так же, как и броуновские частички — блуждает из стороны в сторону, многократно пересекая свою траекторию.

6. Методические рекомендации учителям

1) Рассказывая классу о броуновском движении и диффузии, необходимо сделать акцент на том, что эти явления не доказывают факт существования молекул, но доказывают факт их движения и то, что оно беспорядочное — хаотичное.

2) Обязательно обратите особое внимание на то, что это непрерывное движение, зависящее от температуры, то есть тепловое движение, которое не может прекратиться никогда.

3) Продемонстрируйте диффузию с помощью воды и марганцовки, дав задание наиболее любознательным ребятам провести подобный эксперимент в домашних условиях и делая фотографии воды с марганцовкой через каждый час-два в течение дня (в выходной дети это с удовольствием сделают, а фото пришлют вам). Лучше, если в подобном эксперименте будет две ёмкости с водой — холодной и горячей, чтобы можно было продемонстрировать наглядно зависимость скорости диффузии от температуры.

4) Попробуйте измерить скорость диффузии в классе с помощью, к примеру, дезодоранта — в одном конце класса распыляем небольшое количество аэрозоля, а в 3-5 метрах от этого места ученик с секундомером фиксирует время, через которое он почувствует запах. Это и весело, и интересно, и запомнится детьми надолго!

5) Обсудите с детьми понятие хаотичности и тот факт, что даже в хаотических процессах учёные находят некие закономерности.