Теорема Пифагора
Теорема Пифагора — квадрат гипотенузы равен сумме квадратов катетов (в прямоугольном треугольнике); формула: c² = a² + b².
Доказательство
Доказательство теоремы Пифагора, используя алгебру

Нужно доказать, что c² = a² + b²:
Это квадрат, в котором есть 4 одинаковых треугольника abc:
- Каждая сторона этого квадрата имеет длину a + b, значит его общая площадь: A = (a + b) (a + b);
- Площадь наименьшего квадрата (который находится внутри, под наклоном): c²;
- Площадь каждого из треугольников: ab/2. Значит площадь всех четырёх вместе: 4ab/2 = 2ab;
- Сумма наименьшего квадрата и треугольников: A = c² + 2ab;
- Площадь большого квадрата (A = (a + b) (a + b)) равна сумме наименьшего квадрата со всеми треугольниками. Значит:
(a + b) (a + b) = c² + 2ab
a² + 2ab + b² = c² + 2ab
Что и требовалось доказать.
“Пифагоровы штаны на все стороны равны”
Это шуточная фраза, которая именует ещё одно доказательство теоремы Пифагора

На этой фигуре c — гипотенуза, a и b — катеты.
Проведём перпендикулярную линию к гипотенузе (c):

Таким образом появились два новых прямоугольных треугольника (A и B) внутри большого (исходный треугольник С).
- Общая площадь исходного треугольника (С) равна сумме двух новых, маленьких (A и B): С = А + B;
- Делим “Пифагоровы штаны” на 3 похожие фигуры:

Что и требовалось доказать.
Примеры
Задача 1

На рисунке видно, что длина одной стороны прямоугольного треугольника составляет 3 см, длина другой — 4 см. Найдите длину гипотенузы.
Подставить известные значения
Ответ: длина гипотенузы равна 5.
Задача 2

Длина одной стороны прямоугольного треугольника составляет 12 см, длина гипотенузы 13 см. Найдите длину другой стороны треугольника.
Подставить известные значения
Ответ: длина другой стороны треугольника равна 5.
Следствия из теоремы Пифагора
Это основные следствия теоремы:
- В прямоугольном треугольнике гипотенуза всегда больше любого из двух катетов.
- Если применить формулу теоремы Пифагора (c² = a² + b²) и равенство будет верным, (т.е. если квадрат одной стороны равен сумме квадратов двух других сторон), то треугольник прямоугольный.
- Из формулы теоремы Пифагора также можно посчитать любой из катетов: a² = c² − b² либо b² = c² − a².
- Любой косинус (cos) острого угла будет меньше 1.
Кто придумал теорему Пифагора
Концепция теоремы Пифагора была известна ещё в древнем Египте и Вавилоне (около 1900 г. до н. э.). Связь между катетами и гипотенузой в прямоугольном треугольнике была изображена на вавилонской глиняной табличке (которой около 4000 лет). Однако это знание стало широко использоваться лишь после того, как сам Пифагор заявил о нём (он жил в 6 веке до н. э.).
Узнайте также, что такое Теорема Виета и Аксиома.
Теорема Пифагора
Формула теоремы Пифагора
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов (рис. 1):
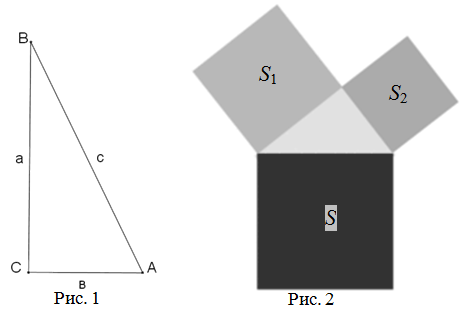
Доказательство теоремы Пифагора
Пусть треугольник $A B C$ – прямоугольный треугольник с прямым углом $C$ (рис. 2).
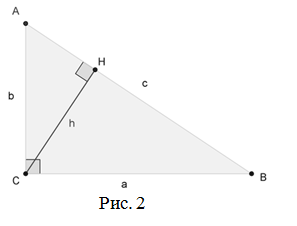
Проведём высоту из вершины $C$ на гипотенузу $A B$, основание высоты обозначим как $H$ .
Прямоугольный треугольник $A C H$ подобен треугольнику $A B C$ по двум углам ( $angle A C B=angle C H A=90^
из подобия треугольников получаем, что
Отсюда имеем, что
$$a^<2>=c cdot H B, b^<2>=c cdot A H$$
Сложив полученные равенства, получаем
$$a^<2>+b^<2>=c cdot H B+c cdot A H$$
Что и требовалось доказать.
Геометрическая формулировка теоремы Пифагора
В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах (рис. 2):
Примеры решения задач
Задание. Задан прямоугольный треугольник $A B C$, катеты которого равны 6 см и 8 см. Найти гипотенузу этого треугольника.
Решение. Согласно условию катеты $a=6$ см, $b=8$ см. Тогда, согласно теореме Пифагора, квадрат гипотенузы
Отсюда получаем, что искомая гипотенуза
Ответ. 10 см
Теорема Пифагора не по зубам? Тебе ответит эксперт через 10 минут!
Задание. Найти площадь прямоугольного треугольника, если известно, что один из его катетов на 5 см больше другого, а гипотенуза равна 25 см.
Решение. Пусть $x$ см – длина меньшего катета, тогда $(x+5)$ см – длина большего. Тогда согласно теореме Пифагора имеем:
Раскрываем скобки, сводим подобные и решаем полученное квадратное уравнение:
Согласно теореме Виета, получаем, что
Значение $x_<2>$ не удовлетворяет условию задачи, а значит, меньший катет равен 15 см, а больший – 20 см.
Площадь прямоугольного треугольника равна полупроизведению длин его катетов, то есть
Ответ. $S=150left(mathrm<см>^<2>right)$
Историческая справка
Теорема Пифагора – одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника.
В древнекитайской книге “Чжоу би суань цзин” говорится о пифагоровом треугольнике со сторонами 3, 4 и 5. Крупнейший немецкий историк математики Мориц Кантор (1829 – 1920) считает, что равенство $3^<2>+4^<2>=5^<2>$ было известно уже египтянам ещё около 2300 г. до н.э. По мнению ученого, строители строили тогда прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5. Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте приводится приближённое вычисление гипотенузы равнобедренного прямоугольного треугольника.
На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии.
Остались вопросы?
Здесь вы найдете ответы.
Согласно теореме Пифагора, значение длины гипотенузы (с) треугольника с прямыми углами, возведенное в квадратную степень, является величиной, равной сумме его катетов (а и b), каждый из которых также возведен в квадрат. Наглядно и с применением условных обозначений это выглядит так:
В теореме Пифагора говорится о том, что в треугольнике с прямыми углами сумма длин катетов, каждая из которых возведена в квадрат, равна длине его гипотенузы, также возведенной в квадратную степень.
При этом под гипотенузой понимается сторона, которая расположена противоположно прямому углу. Катетом считается одна из сторон, участвующих в образовании прямого угла.
Основание прямоугольного треугольника обозначим как Н. Из его вершины С проведем высоту на гипотенузу АВ. Получившийся в результате этого треугольник АСН является подобным треугольнику АВС по двум углам, равным 90º (∠ACB =∠CHA).
В обоих треугольниках есть один общий угол – ∠A.
Подобными также являются треугольные фигуры АВС и СВН. Основанием их подобия являются прямые углы (∠ACB =∠CHB). Оба эти треугольника имеют общий угол, которым является ∠B.
Для продолжения доказательства теоремы Пифагора следует ввести дополнительные обозначения: BC = a, AC = b, AB = c.
На основании полученной ранее информации о подобии треугольников можно утверждать, что:
a/с = HB/a, b/с = AH/b.
Полученное равенство также позволяет сделать следующий вывод:
a2 = c * HB, b2 = c * AH.
На следующем этапе произведем сложение полученных ранее равенств:
a2 + b2 = c * HB + c * AH
Вынесем за скобки общий множитель во второй части равенства:
a2 + b2 = c * (HB + AH)
Теперь можно сократить Н в левой части равенства, в результате получим:
В приведенных выше обозначениях указано, что АВ = с. Это позволяет переписать равенство следующим образом:
a2 + b2 = c * c, или a2 + b2 = c2
Таким образом, теорема Пифагора доказана.
Согласно теореме Пифагора, длина гипотенузы прямоугольного треугольника, которая возведена в квадрат, равна сумме, полученной в результате сложения квадратов длин его катетов. Из этого следует, что:
Извлечем квадрат из обеих частей равенства, в итоге получим:
x = √(5² + 5²)= √(25+25) = √50 = √25*2 = 5√2
Ответ: длина гипотенузы прямоугольного треугольника, катет которого равен 5 см, составляет 5√2, что равно примерно 7,07 см.
Теорема Пифагора не может быть применима к треугольнику с тупыми или острыми углами. Она выполняется только в случае прямоугольного треугольника.
Для треугольника с углом 90º справедливо утверждение о том, что длина его гипотенузы, возведенная во вторую степень, равна сумме длин его катетов, взятых в квадрат.
В теореме Пифагора говорится о том, что сумма длин катетов прямоугольного треугольника, возведенных во вторую степень, равна квадрату длины его гипотенузы. В случае с треугольником, некоторые параметры которого приведены в задании, это утверждение выглядит следующим образом:
х² = 7²-6² = 49-36 = 13.
Для того чтобы найти значение х, нужно извлечь квадратный корень из числа 13:
Ответ: Длина второго катета прямоугольного треугольника равна корню квадратному из 13.
Для решения поставленной задачи следует воспользоваться теоремой Пифагора, которая говорит о том, что сумма длин катетов треугольника с прямым углом, возведенных в квадрат, равна длине его гипотенузы, также возведенной во вторую степень:
Теорема Пифагора может быть применима в данном случае по причине того, что образованная между двумя домами конструкция является прямоугольным треугольником. Зная о том, что сумма квадратов катетов в прямоугольном треугольнике равна длине его катета, возведенной в квадрат, можно вычислить длину неизвестного катета:
24 м – 16 м = 8 м.
Длина одного катета треугольника равна 16 м, второго – 8 м. Зная это, можно применить теорему Пифагора для вычисления длины гипотенузы:
(16*16) + (8*8) = 256 + 64 = 320 м.
Осталось только извлечь квадратный корень из 320, для того чтобы узнать длину расстояния между крышами двух домов.
Ответ: Расстояние между крышами домов равно корню квадратному из 320.
Обозначим длину неизвестного катета как х. Зная то, что по теореме Пифагора длина гипотенузы прямоугольного треугольника, возведенная во вторую степень, равна сумме длин его катетов, которые также возведены в квадрат, можно выразить длину неизвестного катета следующим образом:
х² = 132 – 122 = 169 – 144 = 25
Теперь, для того чтобы узнать длину второго катета, необходимо извлечь квадратный корень из числа 25:
Ответ: длина второго катета прямоугольного треугольника равна 5 см.
Известно, что длина медианы (m), которая проведена к гипотенузе прямоугольного треугольника, равна ½ ее длины. Используя это, можно высчитать длину гипотенузы прямоугольного треугольника:
с = 2*m = 2*6,5 = 13 см.
Высчитав длину гипотенузы и зная длину одного из катетов прямоугольного треугольника, можно вычислить, чему равен его второй катет. Для этого можно использовать теорему Пифагора, согласно которой:
Выражаем из записанного выше равенства длину неизвестного катета:
Из полученного числа нужно извлечь квадратный корень, для того чтобы узнать длину второго катета прямоугольного треугольника:
Ответ: Длина второго катета прямоугольного треугольника равна 12 см.
Равенство, указанное в задании, применимо к треугольнику с прямым углом, как гласит теорема Пифагора.
Каждая из сторон треугольника может быть обозначена прописной буквой, которая соответствует строчной букве, обозначающей угол треугольника, расположенный противоположно этой стороне. На основании этого можно сделать вывод о том, что искомый треугольник является прямоугольным и имеет гипотенузу f и катеты a и b:
Ответ: имеется треугольник АDF с прямым углом F.
Теорема, которая является обратной теореме Пифагора, существует. Согласно этой теореме, треугольник считается прямоугольным в том случае, если длина его большей стороны, возведенная в квадратную степень, равна сумме длин двух других его сторон, которые также возведены в квадратную степень.
Для начала следует провести высоту (h) к основанию равнобедренного треугольника. Данная высота, проведенная к основанию, в случае с равнобедренным треугольником является медианой.
Теперь можно высчитать длину высоты, используя теорему Пифагора. Она будет равна:
h = √((48 см)² – (25,5 см)²) = 10,5√15 см.
Площадь (S) треугольника рассчитывается путем деления на число, полученное в результате умножения длины высоты на длину основания треугольника:
S = ½*10,5√15 см*51 см = 267,75√15 см².
Ответ: Площадь треугольника равна 267,75√15 см².
В равностороннем треугольнике высота (h), проведенная к его основанию, является также его биссектрисой и медианой. Она делит равносторонний треугольник на две части, которые являются равными треугольниками с прямым углом. Их гипотенуза равна а, а катеты – а/2. Для ответа на поставленный вопрос следует применить теорему Пифагора:
Обозначим меньший из катетов как х. Тогда другой катет, длина которого в два раза больше, будет обозначен как 2х. Если в случае с прямоугольным треугольником, длина гипотенузы которого равна √15, применить теорему Пифагора, то она будет выглядеть следующим образом:
После раскрытия скобок в уравнении получаем следующее равенство:
Складываем слагаемые в первой части и получаем:
Сокращаем обе части уравнения на 5, и в итоге получается, что:
Ответ: Длина меньшего из катетов треугольника равна √3, а большего – 2√3.
Если обозначить длину неизвестного катета через х, то гипотенуза будет равна 180-х. Используя введенные обозначения, запишем теорему Пифагора для данного треугольника:
После сокращений получается следующее равенство:
Теперь можно найти значение х:
Длина второго катета равна 80 см.
Зная, что катет в 80 см и неизвестная длина гипотенузы в сумме дают 180 см, можно вычислить длину гипотенузы:
Ответ: Длина гипотенузы равна 100 см.
АВСD является прямоугольной трапецией, у которой AB=9 см и CD=18 см. Диагональ АС данной трапеции составляет 15 см. При этом ВС и AD остаются неизвестными величинами. Длину ВС можно вычислить по следующей формуле:
Произведем перенос высоты:
Тогда получаем, что:
Ответ: Длина основания AD прямоугольной трапеции равна 12+9√3 см.
Различные способы доказательства теоремы Пифагора


Различные способы доказательства теоремы Пифагора
учащаяся 9 «А» класса
Теорема Пифагора по праву считается самой важной в курсе геометрии и заслуживает пристального внимания. Она является основой решения множества геометрических задач, базой для изучения теоретического и практического курса геометрии в дальнейшем. Теорема окружена богатейшим историческим материалом, связанным с её появлением и способами доказательства. Изучение истории развития геометрии прививает любовь к данному предмету, способствует развитию познавательного интереса, общей культуры и творчества, а так же развивает навыки научно-исследовательской работы.
В результате поисковой деятельности была достигнута цель работы, заключающаяся в пополнении и обобщении знаний по доказательству теоремы Пифагора. Удалось найти и рассмотреть различные способы доказательства и углубить знания по теме, выйдя за страницы школьного учебника.
Собранный материал ещё больше убеждает в том, что теорема Пифагора является великой теоремой геометрии, имеет огромное теоретическое и практическое значение.
Введение. Историческая справка 5 Основная часть 8
3. Заключение 19
4. Используемая литература 20
1. ВВЕДЕНИЕ. ИСТОРИЧЕСКАЯ СПРАВКА.
Суть истины вся в том, что нам она – навечно,
Когда хоть раз в прозрении ее увидим свет,
И теорема Пифагора через столько лет
Для нас, как для него, бесспорна, безупречна.
На радостях богам был Пифагором дан обет:
За то, что мудрости коснулся бесконечной,
Он сто быков заклал, благодаря предвечных;
Моленья и хвалы вознес он жертве вслед.
С тех пор быки, когда учуят, тужась,
Что к новой истине людей опять подводит след,
Ревут остервенело, так что слушать мочи нет,
Такой в них Пифагор вселил навеки ужас.
Быкам, бессильным новой правде противостоять,
Что остается? – Лишь глаза закрыв, реветь, дрожать.
Неизвестно, каким способом доказывал Пифагор свою теорему. Несомненно лишь то, что он открыл ее под сильным влиянием египетской науки. Частный случай теоремы Пифагора – свойства треугольника со сторонами 3, 4 и 5 – был известен строителям пирамид задолго до рождения Пифагора, сам же он более 20 лет обучался у египетских жрецов. Сохранилась легенда, которая гласит, что, доказав свою знаменитую теорему, Пифагор принес богам в жертву быка, а по другим источникам, даже 100 быков. Это, однако, противоречит сведениям о моральных и религиозных воззрениях Пифагора. В литературных источниках можно прочитать, что он «запрещал даже убивать животных, а тем более ими кормиться, ибо животные имеют душу, как и мы». Пифагор питался только медом, хлебом, овощами и изредка рыбой. В связи со всем этим более правдоподобной можно считать следующую запись: «. и даже когда он открыл, что в прямоугольном треугольнике гипотенуза имеет соответствие с катетами, он принес в жертву быка, сделанного из пшеничного теста».
Популярность теоремы Пифагора столь велика, что ее доказательства встречаются даже в художественной литературе, например, в рассказе известного английского писателя Хаксли «Юный Архимед». Такое же Доказательство, но для частного случая равнобедренного прямоугольного треугольника приводится в диалоге Платона «Менон».
«Далеко-далеко, куда не летают даже самолеты, находится страна Геометрия. В этой необычной стране был один удивительный город — город Теорем. Однажды в этот город пришла красивая девочка по имени Гипотенуза. Она попробовала снять комнату, но куда бы она ни обращалась, ей всюду отказывали. Наконец она подошла к покосившемуся домику и постучала. Ей открыл мужчина, назвавший себя Прямым Углом, и он предложил Гипотенузе поселиться у него. Гипотенуза осталась в доме, в котором жили Прямой Угол и два его маленьких сына по имени Катеты. С тех пор жизнь в доме Прямого Угла пошла по-новому. На окошке гипотенуза посадила цветы, а в палисаднике развела красные розы. Дом принял форму прямоугольного треугольника. Обоим катетам Гипотенуза очень понравилась и они попросили ее остаться навсегда в их доме. Ло вечерам эта дружная семья собирается за семейным столом. Иногда Прямой Угол играет со своими детишками в прятки. Чаще всего искать приходится ему, а Гипотенуза прячется так искусно, что найти ее бывает очень трудно. Однажды во время игры Прямой Угол подметил интересное свойство: если ему удается найти катеты, то отыскать Гипотенузу не составляет труда. Так Прямой Угол пользуется этой закономерностью, надо сказать, очень успешно. На свойстве этого прямоугольного треугольника и основана теорема Пифагора.»
(Из книги А. Окунева «Спасибо за урок, дети»).
Шутливая формулировка теоремы:
Если дан нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим –
И таким простым путем
К результату мы придем.
Изучая алгебру и начала анализа и геометрию в 10 классе, я убедилась в том, что кроме рассмотренного в 8 классе способа доказательства теоремы Пифагора существуют и другие способы доказательства. Представляю их на ваше обозрение.
2. ОСНОВНАЯ ЧАСТЬ.
Теорема. В прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов.
Пользуясь свойствами площадей многоугольников, установим замечательное соотношение между гипотенузой и катетами прямоугольного треугольника.
Доказательство.
 Рассмотрим прямоугольный треугольник с катетами а, в и гипотенузой с (рис.1, а).
Рассмотрим прямоугольный треугольник с катетами а, в и гипотенузой с (рис.1, а).
 Докажем, что с²=а²+в².
Докажем, что с²=а²+в².
 Доказательство.
Доказательство.
 Достроим треугольник до квадрата со стороной а + в так, как показано на рис. 1, б. Площадь S этого квадрата равна (а + в)² . С другой стороны, этот квадрат составлен из четырех равных прямоугольных треугольников, площадь каждого из которых равна ½ав , и квадрата со стороной с, поэтому S= 4 * ½ав + с² =2ав + с².
Достроим треугольник до квадрата со стороной а + в так, как показано на рис. 1, б. Площадь S этого квадрата равна (а + в)² . С другой стороны, этот квадрат составлен из четырех равных прямоугольных треугольников, площадь каждого из которых равна ½ав , и квадрата со стороной с, поэтому S= 4 * ½ав + с² =2ав + с².
(а + в)² = 2ав + с²,
Теорема доказана.  2 СПОСОБ.
2 СПОСОБ.
После изучения темы «Подобные треугольники» я выяснила, что можно применить подобие треугольников к доказательству теоремы Пифагора. А именно, я воспользовалась утверждением о том, что катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключённого между катетом и высотой, проведённой из вершины прямого угла.
 Рассмотрим прямоугольный треугольник с прямым углом С, СD– высота (рис. 2). Докажем, что АС² +СВ² = АВ².
Рассмотрим прямоугольный треугольник с прямым углом С, СD– высота (рис. 2). Докажем, что АС² +СВ² = АВ².

На основании утверждения о катете прямоугольного треугольника:
АС =  , СВ =
, СВ =  .
.
Возведем в квадрат и сложим полученные равенства:
АС² = АВ * АD, СВ² = АВ * DВ;
АС² + СВ² = АВ * ( АD + DВ), где АD+DB=AB, тогда
Доказательство закончено.
3 СПОСОБ.
К доказательству теоремы Пифагора можно применить определение косинуса острого угла прямоугольного треугольника. Рассмотрим рис. 3.


Пусть АВС – данный прямоугольный треугольник с прямым углом С. Проведем высоту СD из вершины прямого угла С.
По определению косинуса угла:
cos А = АD/АС = АС/АВ. Отсюда АВ * АD = АС²
cos В = ВD/ВС = ВС/АВ.
Отсюда АВ * ВD = ВС² .
Складывая полученные равенства почленно и замечая, что АD + DВ = АВ, получим:
АС² + ВС² = АВ (АD + DВ) = АВ²
Доказательство закончено.
4 СПОСОБ.
Изучив тему «Соотношения между сторонами и углами прямоугольного треугольника», я думаю, что теорему Пифагора можно доказать ещё одним способом.
Рассмотрим прямоугольный треугольник с катетами а, в и гипотенузой с. (рис. 4).


Докажем, что с²=а²+в².
sinВ= в/с ; cosВ= a/с, то, возведя в квадрат полученные равенства, получим:
sin²В= в²/с²; cos²В= а²/с².
Сложив их, получим:
sin²В + cos²В= в²/с²+ а²/с², где sin²В + cos²В=1,
1= (в²+ а²) / с², следовательно,
с²= а² + в².
 Данное доказательство основано на разрезании квадратов, построенных на катетах (рис. 5), и укладывании полученных частей на квадрате, построенном на гипотенузе.
Данное доказательство основано на разрезании квадратов, построенных на катетах (рис. 5), и укладывании полученных частей на квадрате, построенном на гипотенузе.

Для доказательства на катете ВС строим  BCD ABC (рис.6 ). Мы знаем, что площади подобных фигур относятся как квадраты их сходственных линейных размеров:
BCD ABC (рис.6 ). Мы знаем, что площади подобных фигур относятся как квадраты их сходственных линейных размеров:

Вычитая из первого равенства второе, получим
 ,
,
 ,
,
 с2 = а2 + b2.
с2 = а2 + b2.
Дано (рис. 7):
 ABС,
ABС,  = 90°, ВС = а, АС=b, АВ = с.
= 90°, ВС = а, АС=b, АВ = с.
Доказать: с2 = а2 + b2.


Доказательство.
Пусть катет b а. Продолжим отрезок СВ за точку В и построим треугольник BMD так, чтобы точки М и А лежали по одну сторону от прямой CD и, кроме того, BD = b, BDM = 90°, DM = a, тогда  BMD =
BMD =  ABC по двум сторонам и углу между ними. Точки А и М соединим отрезками AM. Имеем MD CD и AC CD, значит, прямая АС параллельна прямой MD. Так как MD
ABC по двум сторонам и углу между ними. Точки А и М соединим отрезками AM. Имеем MD CD и AC CD, значит, прямая АС параллельна прямой MD. Так как MD
Геометрия
Именная карта банка для детей
с крутым дизайном, +200 бонусов
Закажи свою собственную карту банка и получи бонусы
План урока:
Теорема Пифагора
Попытаемся установить связь между гипотенузой и катетами прямоугольного треугольника. Пусть в некотором прямоугольном треуг-ке катеты имеют длины а и b, а гипотенуза равна с. Пусть один из острых углов треуг-ка составляет α, тогда другой острый угол должен равняться 90 – α:
Далее возьмем 4 таких треуг-ка и расположим их следующим образом:
Здесь мы прикладываем треуг-ки так, чтобы их разные катеты образовали одну сторону четырехугольника. В результате получается большой квадрат со стороной a + b. Квадратом он является по определению, ведь все его стороны одинаковы, а углы – прямые.
Изучим центральную фигуру, чью площадь мы обозначили как S2. Это четырехуг-к, причем все его стороны равны с, то есть длине гипотенузы треугольника. С другой стороны, каждый его угол можно найти, вычтя из 180° величины α и 90° – α:
Получается, что всего его углы прямые, то есть он является квадратом. Найдем его площадь:
Вернемся к большому квадрату. С одной стороны, его площадь можно записать как сумму площадей фигур, его составляющих:
Cдругой стороны, эту же площадь можно найти, просто возведя в квадрат его сторону:
Получили формулу, в которой и заключен смысл теоремы Пифагора:
Изучим несколько простейших примеров использования теоремы Пифагора.
Задание. Длины катетов прямоугольного треугольника составляют 5 и 12. Определите длину гипотенузы.
Решение. Запишем теорему Пифагора:
Задание. Длина катета треугольника составляет 3, а гипотенузы – 5. Какова длина другого катета?
Решение: На это раз нам известен один из катетов а = 3 и гипотенуза с = 5. Подставим в теорему Пифагора эти числа:
Теорема Пифагора имеет огромное значение для геометрии и смежных дисциплин. Приведенное здесь ее доказательство является одним из простейших, но отнюдь не единственным. Сегодня человечеству известно 367 различных доказательств теоремы Пифагора, что лишь показывает ее огромную значимость.
На самом деле Пифагор, известный древнегреческий математик, не был первым, кто обнаружил это равенство. Пифагор родился примерно в 570 г. до н. э., однако ещё египтяне знали про прямоугольный треуг-к со сторонами 3, 4 и 5. Поэтому его часто именуют египетским треугольником.
Также вычислять стороны прямоугольного треуг-ка умели и в Вавилоне уже за 1000 лет до рождения Пифагора. Вероятно, Пифагор узнал о формуле от вавилонян, а сам лишь вывел ее доказательство (вавилоняне не утруждали себя необходимостью доказывать теоремы геометрии). Утверждается, что Пифагор принес сделал жертвоприношение в размере 100 быков после того, как смог доказать теорему.
Задание. Вычислите гипотенузу равнобедренного прямоугольного треуг-ка, чьи катеты имеют единичную длину.
Решение. В теорему Пифагора вместо букв a и b подставим единицу:
Обратите внимание, что в данной задаче в качестве длины гипотенузы прямоугольного треугольника получилось иррациональное число. Исторически именно при решении подобной задачи люди (это были ученики Пифагора) впервые столкнулись с иррациональными числами. Перед дальнейшим изучением темы есть смысл вспомнить основные правила вычислений с квадратными корнями.
Задание. На рисунке построен произвольный квадрат. Предложите способ, как построить квадрат с вдвое большей площадью.
Решение. Проведем в исходном квадрате диагональ. Далее построим новый квадрат со стороной, равной этой гипотенузе:
Докажем, что получившийся квадрат (его стороны отмечены синим цветом) вдвое больше исходного квадрата. Пусть сторона изначального квадрата равна х.Тогда его площадь составляет х 2 . Диагональ разбивает квадрат на два прямоугольных треуг-ка, в которых она является гипотенузой.
Запишем для одного из них теорему Пифагора:
Но площадь квадрата равна его стороне, возведенной во вторую степень, поэтому величина с 2 – это площадь большого (на рисунке – синего)квадрата, а х 2 – площадь маленького:
Подставим эти выражения в формулу, выведенную из теоремы Пифагора, и получим, что площадь большего квадрата ровно вдвое больше:
Задание. Найдите площадь равнобедренного прямоугольного треуг-ка, гипотенуза которого имеет длину 10.
Решение. Обозначим катеты переменной х, тогда теорема Пифагора будет выглядеть как уравнение:
Задание. Один из острых углов прямоугольного треугольника составляет 30°, а его гипотенуза равна 10. Найдите оба катета.
Решение. Мы знаем, что в прямоугольном треуг-ке с острым углом 30° гипотенуза вдвое длиннее меньшего катета (он как раз лежит против угла 30°), мы можем найти этот катет:
Другой катет находим с помощью теоремы Пифагора:
Задачи на применение теоремы Пифагора
Теорема Пифагора используется в огромном количестве геометрических задач. С ее помощью можно находить диагонали некоторых четырехуг-ков, длины высот, вычислять площади.
Задание. Стороны прямоуг-ка имеют длину 8 и 15 см. Найдите длину его диагонали.
Решение. Рассмотрим произвольный прямоугольник АВСD. Если в нем провести диагональ ВD, то получится прямоугольный треуг-к АВD. Пусть АВ = 15, АD = 8. Запишем теорему Пифагора для ∆АВD:
Задание. В равнобедренном треуг-ке основание имеет длину 16 см, а боковые стороны составляют 17 см. Найдите длину высоты, проведенной к основанию этого треуг-ка, а также площадь треуг-ка.
Решение. Напомним, что высота, опущенная к основанию равнобедренного треуг-ка, одновременно является и медианой, и биссектрисой. Это значит, что Н – середина АВ. Тогда можно найти длину отрезков АН и НВ:
Теперь можно рассмотреть ∆АСН. Он прямоугольный, и нам известно его гипотенуза (она является боковой стороной ∆АВС и по условию равна 17 см) и катет АН. Тогда можно найти и второй катет, то есть высоту СН:
Задание. Высота равностороннего треуг-ка составляет 4 см. Найдите его сторону.
Решение. Напомним, что в равностороннем треуг-ке все углы равны 60°. Также учтем, что высота в равностороннем треуг-ке является также и биссектрисой и медианой:
Рассмотрим ∆АСН. Он прямоугольный, и один из его углов составляет 60°. Значит, другой угол составляет 30°. Но в таком треуг-ке гипотенуза вдвое больше катета, лежащего против ∠30°:
Обратите внимание, мы специально домножили дробь на корень из 3, чтобы корень оказался в числителе, а не знаменателе. Т.к. в таком виде проще работать с квадратными корнями.
Итак, мы нашли АН. Теперь можно найти сторону АС, которая вдвое длиннее:
Задание. Составьте формулу для нахождения площади равностороннего треуг-ка, если известна только его сторона.
Решение. Обозначим сторону треуг-ка буквой а. Для вычисления площади необходимо найти высоту:
Как и в предыдущей задаче, отрезок АС вдвое длиннее АН:
Высоту мы нашли. Осталось найти площадь:
Задание. В прямоугольном треуг-ке, катеты которого имеют длину 60 и 80, проведена высота к гипотенузе. Найдите высоту гипотенузы, а также длину отрезков, на которые эта высота разбивает гипотенузу.
Решение. Найдем длину гипотенузы ВС:
Осталось найти длины отрезков СН и НВ. Для этого необходимо записать теорему Пифагора для ∆АСН и ∆АНВ, которые являются прямоугольными. Начнем с ∆АСН:
Аналогично работаем и с ∆АНВ:
Можно проверить себя. Отрезки НВ и СН вместе составляют отрезок СВ, поэтому должно выполняться равенство:
Задание. Диагонали ромба равны 10 и 24 см. Чему равна его сторона?
Пусть в ромбе АВСD диагонали пересекаются в точке О, причем АС = 24 см, а ВD = 10 см.Напомним, что диагонали ромба пересекаются под углом 90° и делятся при этом на одинаковые отрезки. Следовательно, ∆АВО прямоугольный. Найдем его катеты:
Задание. Основания равнобедренной трапеции имеют длину 20 и 10, а боковая сторона имеет длину 13. Найдите площадь трапеции.
Решение. Опустим на большее основание две высоты:
В итоге получили прямоуг-к АВКН. Его противоположные стороны одинаковы, поэтому
∆АНD и ∆ВКС равны друг другу, ведь это прямоугольные треуг-ки с одинаковой гипотенузой (АD = ВС, ведь это равнобедренная трапеция) и равным катетом (АН = ВК как стороны прямоуг-ка). Это значит, что DH = КС. Но эти отрезки вместе с НК составляют CD. Это позволяет найти DH и KC:
Зная высоту трапеции и ее основания, легко найдем и ее площадь:
Пифагоровы тройки
Возможно, вы уже заметили, что в большинстве школьных задач на применение теоремы Пифагора используются треуг-ки с одними и теми же сторонами. Это треуг-к, чьи стороны имеют длины
Их использование обусловлено тем, что все их стороны выражаются целыми числами. В задачах же, например, с равнобедренным прямоугольным треуг-ком хотя бы одна из сторон обязательно оказывается иррациональным числом.
Прямоугольные треуг-ки, у которых все стороны являются целыми, называют пифагоровыми треугольниками, а длины их сторон именуются пифагоровыми тройками. Получается, что пифагоровыми называются такие тройки натуральных чисел а, b и с, которые при подстановке в уравнение
обращают его в справедливое равенство.
Для удобства такие тройки иногда записывают в скобках.
Например, тройка чисел (3; 4; 5)– пифагорова, так как
Задание. Определите, какие из следующих троек чисел являются пифагоровыми:
Несложно догадаться, что пифагоровых троек существует бесконечно много. Действительно, возьмем тройку (3; 4; 5). Далее умножим все числа, составляющие ее, на два, и получим новую тройку (6; 8; 10), которая также пифагорова. Умножив исходную тройку на 3, получим тройку (9; 12; 15), и она снова пифагорова. Вообще, умножая числа пифагоровой тройки на любое натуральное число, всегда будем получать новую пифагорову тройку. А так как натуральных чисел бесконечно много, то и троек Пифагора также бесконечное количество.
Отдельно выделяют понятие примитивной пифагоровой тройки. Эта такая тройка, числа которой являются взаимно простыми, то есть не имеют общих делителей. Другими словами, примитивная тройка НЕ может быть получена из другой тройки простым умножением ее чисел на натуральное число. В частности, тройка (3; 4; 5)является примитивной, а «производные» от нее тройки (6; 8; 10) и (9; 12; 15) уже не примитивные.
Интересно, что примитивных троек также бесконечно много. Ещё Евклид предложил алгоритм для их поиска, который, однако, не изучается в рамках школьного курса геометрии.
Задание. Докажите, что у любого прямоугольного треуг-ка с целыми длинами сторон все эти длины не могут быть нечетными числами.
Предположим, что такой треуг-к существует. Пусть его стороны равны a, b и c, и эти числа нечетны. Тогда должно выполняться уравнение:
Заметим, что квадрат нечетного числа также является нечетным числом. Поэтому числа а 2 , b 2 и с 2 – нечетные. Однако сумма нечетных чисел является уже четной. Поэтому выражение а 2 + b 2 четное. Таким образом, получается, что равенство
не может быть верным, ведь его левая часть четна, а правая – нечетна. Поэтому пифагоров треуг-к с тремя нечетными сторонами существовать не может.
Обратная теорема Пифагора
По теореме Пифагора из того факта, что в треуг-ке есть прямой угол, следует следующее соотношение между длинами его сторон:
Оказывается, верно и обратное: если в произвольном треуг-ке одна сторона (очевидно, большая из них) равна сумме квадратов двух других сторон, то из этого следует, что такой треуг-к является прямоугольным.
Это утверждение называют обратной теоремой Пифагора. Докажем её. Пусть есть некоторый ∆АВС, для сторон которого выполняется равенство
Так как ∆А1В1С1 прямоугольный, то для него справедлива теорема Пифагора. Найдем с ее помощью гипотенузу:
а именно это мы и доказываем.
Уточним разницу между собственно теоремой Пифагора и только что доказанной обратной ей теореме. В каждой теореме есть две ключевые части:
1) некоторое условие, которое описывает какое-то геометрическое построение;
2) вывод (или заключение), который делается для условия.
В самой теореме Пифагора в качестве условия описывается прямоугольный треугольник. Для него делается вывод – катеты, возведенные в квадрат, в сумме дадут квадрат гипотенузы.
В обратной же теореме условие и вывод меняются местами. В роли условия описывается треугольник, у которого большая сторона, возведенная во 2-ую степень, равна сумме двух других сторон, также возведенная в квадрат. Для этого описания делается вывод – такой треугольник обязательно должен быть прямоугольным.
Заметим, что не всякая обратная теорема является справедливой. Например, одна из простейших теорем гласит – если углы вертикальные, то они равны. Сформулируем обратную теорему – если углы равны, то они вертикальные. Понятно, что это неверное утверждение.
Задание. Выясните, является ли треуг-к прямоугольным, если его стороны имеют длины:
Решение. Здесь надо просто проверить, являются ли эти числа пифагоровыми тройками. Если являются, то соответствующий треуг-к окажется прямоугольным.
Задание. В ∆КМР проведена биссектриса МН. Её длина 12. КМ = 13 и КН = 5. Найдите МР.
Решение. Рассмотрим ∆МНК. Его стороны равны 5, 12 и 13. Но это одна из пифагоровых троек:
Отсюда следует, что треуг-к прямоугольный, причем МК – гипотенуза (гипотенуза – это длиннейшая сторона). Тогда ∠Н = 90°. Но это означает, что биссектриса МН ещё и высота. Но если в треугольнике одна линия одновременно и медиана, и высота, то это равнобедренный треуг-к, причем КР – его основание. Тогда
Формула Герона
Невозможно построить два треугольника с тремя одинаковыми сторонами. Это значит, что теоретически знания трех сторон треугольника достаточно, чтобы найти его площадь. Но как это сделать? Здесь может помочь формула Герона, которая выводится с помощью теоремы Пифагора.
Пусть стороны треуг-ка равны а, b и с, причем с не меньше, чем а и b. В любом треуг-ке есть хотя бы два острых угла, а тупой угол, если он есть, лежит против большей стороны. Это значит, что оба прилегающих кс угла – острые. Отсюда следует, что высота, опущенная нас, будет лежать внутри треуг-ка. Обозначим длину этой высоты как h. Пусть она разобьет сторону сна два отрезка длиной х и у:
По рисунку можно записать три уравнения:
Левая часть одинакова в обоих уравнениях, значит, равны и правые:
С учетом этого выразим h 2 :
Мы уже выразили высоту (точнее, ее квадрат) через длины сторон. Однако обычно в этой формуле производят замену и вводят число р, равное полупериметру треуг-ка, то есть
Площадь треуг-ка вычисляется по формуле:
Запоминать вывод формулы Герона не надо. Саму формулу всегда можно найти в любом справочнике по геометрии или в Интернете. Достаточно запомнить, что площадь любого треуг-ка можно вычислить, если известны все его стороны.
Задание. Стороны треуг-ка имеют длину 9, 7 и 8 см. Какова его площадь?
Решение. Пусть а = 9; b = 8; с = 7. Для использования формулы Герона сначала вычислим половину периметра треуг-ка:
Итак, сегодня мы узнали о теореме Пифагора. Она представляет собой соотношение, которое связывает катеты и гипотенузу в прямоугольном треуг-ке. Это соотношение помогает в исследованиях других фигур – квадратов, параллелограммов, трапеций. Также с его помощью выведена формула Герона, которая позволяет вычислять площадь треуг-ка, зная только длины его сторон.
Доказательства теоремы Пифагора
- Теорема Пифагора — краткая история
- Формулировка теоремы
- Уравнение
- Доказательство через подобные треугольники
- Другие способы доказательства теоремы
- Методом площадей
- Методом бесконечных малых
- Следствие из теоремы Пифагора
- Применение теоремы
- Расстояние между точками
- Евклидова метрика
- Теория чисел
- Примеры решения задач
Этот одна из базовых теорем евклидовой геометрии, определяющая соотношение между сторонами в прямоугольном треугольнике. Несложность доказательства и широкое применение обеспечили ей массовую известность.
Теорема Пифагора — краткая история
Соотношение между сторонами прямоугольного треугольника в том или ином виде было известно многим древним цивилизациям (египетской, шумерской и др.), но первая известная формулировка принадлежит греческому философу и математику Пифагору в V в. до н.э. Об этом известно из труда «Начала», который написал Евклид приблизительно в 300 г. до н. э.
Теорема Пифагора используется для доказательства многих других теорем геометрии. Математиками разработано несколько обобщений, например, для произвольных треугольников, для многомерных пространств. При этом, теорема Пифагора выполняется только в евклидовых геометриях, в иных случаях она не действует.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Формулировка теоремы
Изначальная (геометрическая) формулировка Пифагора гласила:
В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.
Позднее появился алгебраический вариант:
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Оба этих определения эквивалентны. Алгебраическое более элементарно, так как оно не оперирует понятием площади, поэтому теорему в этом виде можно проверить просто – измерив длину гипотенузы и катетов, сделав затем необходимое вычисление.
Уравнение
В виде формулы теорема Пифагора записывается следующим образом:
a 2 +b 2 =c 2 , где:
- а и b – длины двух катетов,
- с – длина гипотенузы.
Доказательство через подобные треугольники
Это доказательство – одно из наиболее простых, так как является прямым следствием аксиом и не оперирует понятием площади.
Имеется прямоугольный треугольник ABC, где C = 90º. Высота, проведенная из прямого угла пересечет гипотенузу в точке H.
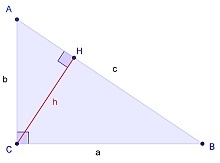
Полученные треугольники ACH и CHB подобны треугольнику АВС по двум углам. Отсюда получаем:
CB 2 =ABxHB, AC 2 =ABxAH
Сложив между собой квадраты катетов, получаем:
AC 2 +CB 2 =ABx(HB+AH)=AB 2
Это и требовалось доказать.
Другие способы доказательства теоремы
Зафиксировано более 400 доказательств теоремы Пифагора. Это связано с простотой ее формулировки, популярностью и широким применением в геометрии. К числу распространенных доказательств относятся методы площадей и бесконечно малых.
Методом площадей
Первоначально требуется дополнительное построение – рисуется квадрат, каждая из сторон которого равна сумме длин катетов a и b. Отложив эти длины, проведем гипотенузы у прямоугольных треугольников:
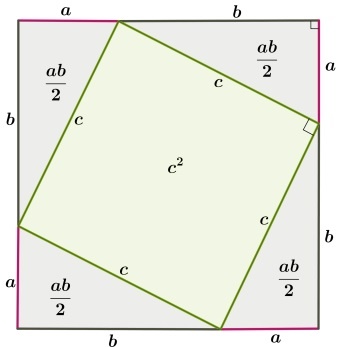
Очевидно, что внутренний четырехугольник, образованный четырьмя гипотенузами, будет квадратом, так как все его стороны равны, а углы прямые. Последнее следует из того, что сумма двух углов треугольника, построенных на гипотенузе равна 90º. Вычитая это значение из развернутого угла в 180º получаем как раз прямой угол.
Площадь внешнего квадрата включает в себя:
- сумму площадей четырех прямоугольных треугольников;
- площадь внутреннего квадрата.
Изменив расположение отрезков на сторонах квадрата и проведя новое построение, можно получить два внутренних квадрата и два прямоугольника. При этом, прямоугольники всегда будут равны, а квадраты будут равными только в частном случае – при равенстве сторон a и b.
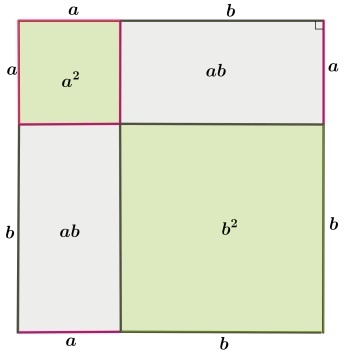
4ab 2 =2ab ⇒ c 2 =a 2 +b 2 , что и нужно было доказать.
Методом бесконечных малых
Данное доказательство делается с помощью интегрального исчисления. Рассматривается ситуация для бесконечно малых приращений сторон треугольника, составляется дифференциальное уравнение и находится его производная.
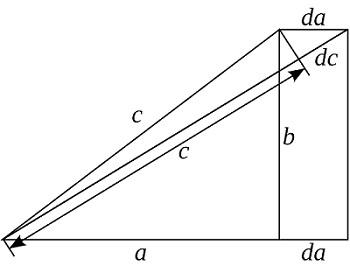
В начале вводится величина d. На это значение увеличивается катет а и гипотенуза с, а катет b остается неизменным. Отсюда имеем
da/ca = c/a, b = const
Разделяя переменные составляется дифференциальное уравнение:
Для его решения необходимо проинтегрировать обе части, при этом получается соотношение:
c 2 = a 2 + const
определяя из начальных условий константу интегрирования, получим:
a = 0 ⇒ c 2 = b 2 = const
Таким образом мы определяем, что
Следствие из теоремы Пифагора
Его так же называют обратной теоремой Пифагора:
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то такой треугольник прямоугольный.
В алгебраическом виде это можно представить так:
c2=a2+b2, где:
- c – гипотенуза треугольника;
- a и b – его катеты.
Применение теоремы
Благодаря своей универсальности, теорема Пифагора находит себе применение в разных областях математики и других наук. К числу преимуществ ее применения относится прозрачность производимых вычислений.
Расстояние между точками
Одно из главных применений – это определение расстояния между двумя точками в прямоугольной системе координат:
- s – необходимое расстояние;
- (a; b) и (с; d) – координаты двух точек.
Евклидова метрика
В этом случае с помощью теоремы Пифагора находится расстояние в многомерном пространстве:
- n – число измерений данного пространства;
- d (p, q) – необходимое расстояние;
- p(p1,….,pn) и q(q1,….,qn) – две точки, расстояние между которыми нужно найти.
Теория чисел
Арифметическим аналогом теоремы Пифагора стали пифагоровы тройки чисел.
Пифагоровы тройки – группа из трех натуральных чисел x, y и z, удовлетворяющих равенству x2+y2=z2.
Например, к таким числам можно отнести группы (3, 4, 5), (6, 8, 10), (5, 12, 13) и другие. Пифагоровы тройки широко применяются в разных областях деятельности, например, в программировании и криптографии.
Примеры решения задач
Задача 1
В прямоугольном треугольнике АВС, катет ВС = 36 см, гипотенуза АВ = 85 см. Необходимо найти катет АС.
Решение
По теореме Пифагора ВС 2 +АС 2 =АВ 2 , значит
Для нахождения ответа подставим в формулу исходные значения:
Задача 2
Является ли прямоугольным треугольник со сторонами 46, 56 и 76 см.
Решение. Если указанный треугольник прямоугольный, то две меньшие стороны в 46 и 56 см – это катеты, а большая, в 76 см – гипотенуза. По теореме Пифагора сумма квадратов катетов должна быть равна квадрату гипотенузы. Проверим это:
- 46²+56²= 5252;
- 76²= 5776;
- 5252 ≠ 5776, значит, указанный треугольник не является прямоугольным.
Задача 3.
Диагонали ромба ABCD равны 24 и 18 см. Чему равна сторона ромба.
Решение
Диагонали ромба AC и BD пересекаются под прямым углом и точкой пересечения O делятся пополам. В этом виде задача сводится к поиску гипотенузы АВ в прямоугольном треугольнике ABO с катетами АО=24/2=12 см и ВО=18/2=9 см.
Теорема Пифагора: история, формулы и доказательства

Теорема Пифагора – одна из самых известных геометрических теорем, которая устанавливает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Большинство ученых считают, что теорема Пифагора была доказана древнегреческим математиком и философом Пифагором (или Питагором). Однако есть версия, что теорему знали и до его рождения. Доказательством этого является то, что в Древнем Египте знали, что треугольник, у которого стороны имеют 3 см, 4 см и 5 см, является прямоугольным. А о других теоремах можно узнать в учебнике по геометрии за 8 класс А.Г. Мерзляка.
Еще в детстве Пифагор отличился интересом к точным наукам. Впоследствии он переехал жить на остров Лесбос, где познакомился с Фалесом Милетским – древнегреческим философом и математиком, который доказал теоремы о трех точках на окружности и пропорциональных отрезках. За время, когда Пифагор учился в Милетской школе, он изучал астрологию, медицину, прогнозы затмений и другие важные в то время науки. Лекции Фалеса и его ученика Анаксимандра сыграли важную роль для Пифагора.
После обучения в Египте, плена в Вавилоне, в 60 лет Пифагор решает вернуться домой, чтобы поделиться своими знаниями с народом. Впоследствии он открыл собственную школу, в которой геометрия впервые выступает как самостоятельная наука.
О том, что квадрат гипотенузы равен сумме квадратов катетов, знали задолго до рождения Пифагора. Но именно он считается первым ученым, который доказал соотношение сторон треугольника.
В теореме Пифагора говорится, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Пусть ВС = а; АС = b; АВ = с.
Тогда имеем такую формулу, которая применяется при нахождении неизвестной стороны в прямоугольном треугольнике, когда две другие – известны:
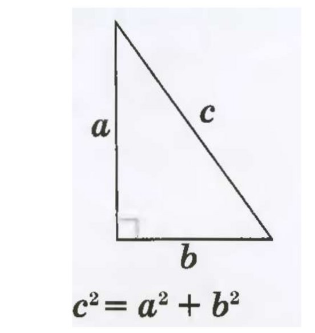
Когда мы определили квадрат гипотенузы, нужно найти квадратный корень. Такую же формулу мы можем применить к неизвестному катету:

А больше рисунков и формул можно увидеть в онлайн уроке за 8 класс по геометрии на тему “Метрические соотношения в прямоугольном треугольнике. Теорема Пифагора”.
Самый популярный и самый простой метод доказательства теоремы связан с площадями фигуры.
Нужно расположить одинаковые прямоугольные треугольники так, чтобы внутри образовался квадрат. Каждая сторона внешнего квадрата должна состоять из суммы катетов прямоугольного треугольника a + b.

Площадь этого квадрата можно будет найти благодаря формуле:
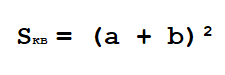
Внутренний четырехугольник можно считать квадратом, ведь, если добавить два острые углы прямоугольного треугольника, то получится 90°. Следует считать, что площадь внешнего квадрата состоит из площади внутреннего квадрата и четырех площадей одинаковых прямоугольных треугольников. Итак, в заключении:
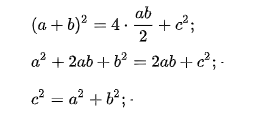
Итак, теорема Пифагора доказана.
2. Доказательство Евклида
Доказательство Евклида также называется “Пифагоровы штаны”. Ее так назвали, потому что сумма площади квадратов, образованных с использованием катетов прямоугольного треугольника равна площади квадрата, который построен на гипотенузе этого же треугольника. Квадраты напоминали ученикам мужские штаны.
На примере приведенных картинок ниже можно увидеть, как оригинально передали суть доказательства Евклида.


В вашем учебнике не было таких доказательств? Вы можете найти другой в разделе “Учебники по геометрии за 8 класс”.
Пример задачи на применение теоремы Пифагора
Условия задачи. В треугольнике ABC дано: ∠C = 90 °, BC = 20 см, AC = 15 см. Найти сторону AB.

Решение. Поскольку в треугольнике АВС ∠С = 90°, следовательно, по теореме Пифагора имеем:
АВ² = BС² + АС²; AВ² = 20² + 15², AВ² = 625, AB = √625| AB = 25 см.
Если вам нужно решить задачу с помощью теоремы Пифагора, а вы сомневаетесь в конечном ответе, тогда можете проверить свои знания благодаря разделу “ГДЗ и решебники по геометрии за 8 класс”.
А если вы хотите крепче закрепить знания по другим темам по геометрии, то можете просматривать видео в разделе “Онлайн уроки за 8 класс по геометрии”. Узнайте больше о перпендикуляре и наклонной, сумме углов выпуклого треугольника, площадь квадрата и прямоугольника, решение задач методом площадей и тому подобное.
Малоизвестное обобщение теоремы Пифагора
Вокруг да около
История теоремы Пифагора уходит в века и тысячелетия. В этой статье, мы не будем подробно останавливаться на исторических темах. Для интриги, скажем только, что, по-видимому, эту теорему знали еще древне-египетские жрецы, жившие более 2000 лет до нашей эры. Для тех, кому любопытно, вот ссылка на статью в Википедии.
Прежде всего, хочется для полноты изложения привести здесь доказательство теоремы Пифагора, которое, по моему мнению, наиболее элегантно и очевидно. На рисунке выше изображено два одинаковых квадрата: левый и правый. Из рисунка видно, что слева и справа площади закрашенных фигур равны, так как в каждом из больших квадратов закрашено по 4 одинаковых прямоугольных треугольника. А это означает, что и незакрашенные (белые) площади слева и справа тоже равны. Замечаем, что в первом случае площадь незакрашенной фигуры равна , а во втором — площадь незакрашенной области равна
. Таким образом,
. Теорема доказана!
Зарождение идеи
В этой статье я хочу не только рассказать что-то новое и познавательное о теореме Пифагора, но и поделиться своей историей о том, как в моей голове зародилась интересная идея, которую я сумел сформулировать, доказать и даже предположил возможность обобщения на более высокую размерность. Но обо всем по порядку.
Египетские треугольники
Во-первых, это красивые математические объекты. А во-вторых, с ними очень удобно решать задачи! Нет никаких квадратных корней и иррациональных чисел в ответе.
Загадочные четверки
Заметив такое удивительное совпадение, я стал думать. Вопрос, который меня занимал в связи с этим загадочным обстоятельством, наличием не только троек, но и четверок, обнаруживающих свойства египетского треугольника, был таков: “А что бы это все могло значить?” Я перебирал варианты, какие только приходили в голову. В фантазии себя никак не ограничивал. Много раз садился за стол, выписывал известные мне наборы четверок и вдумчиво на них смотрел… часами… без перерыва… и… ничего не происходило. У меня был школьный товарищ Саня, с которым я как-то поделился своими идеями. Но его больше интересовали гуманитарные науки. Он стал юристом и сейчас служит в звании майора милиции. Саня сказал мне примерно следующее:«Вот странный ты человек. Делать тебе больше нечего. Мало тебе задают домашек? Хватит думать о всякой ерунде!». А, надо сказать, думал я, не переставая, и думал много лет, время от времени возвращаясь к этой загадке. Еще будучи школьником, я сделал вывод, что это, вероятнее всего, имеет отношение к великой теореме Ферма (на которую я тоже много раз подолгу смотрел). Шли годы. Ничего не получалось. Озарение не приходило. И я понял, что, вероятно, дальше чем «что-то связанное с теоремой Ферма» я никуда уже не продвинусь. Но не тут то было
Шерлок нашел зацепку
Итак, в 2014 году ехал я в автобусе по Новосибирску. А может быть это было метро. Дорога не близкая. Заняться нечем. И в очередной раз решил я подумать о моей школьной загадке. И вот что я подумал.
Как же назвать эти числа? Треугольниками не назовешь, ведь четыре числа никак не могут образовать треугольник. И тут! Как гром среди ясного неба
Раз есть такие четверки чисел, значит должен быть геометрический объект с такими же свойствами, отраженными в этих числах!
Теперь осталось только подобрать какой-то геометрический объект под это свойство, и все встанет на свои места! Конечно, предположение было чисто гипотетическое, и никакого подтверждения под собой не имело. Но что если это так!
Начался перебор объектов. Звезды, многоугольники, правильные, неправильные, с прямым углом и так далее и тому подобное. Опять ничего не подходит. Что делать? И в этот момент Шерлок получает свою вторую зацепку.
Надо повысить размерность! Раз тройке соответствуют треугольник на плоскости, значит четверке соответствует нечто трехмерное!
О нет! Опять перебор вариантов! А в трехмерии гораздо, гораздо больше всевозможных геометрических тел. Попробуй перебрать их все! Но не все так плохо. Есть же еще прямой угол и другие зацепки! Что мы имеем? Египетские четверки чисел (пусть будут египетские, надо же их как-то называть), прямой угол (или углы) и некий трехмерный объект. Дедукция сработала! И… Полагаю, что догадливые читатели уже поняли, что речь идет о пирамидах, у которых при одной из вершин все три угла — прямые. Можно даже назвать их прямоугольными пирамидами по аналогии с прямоугольным треугольником.
Новая теорема
Итак, у нас есть все что нужно. Прямоугольные (!) пирамиды, боковые грани-катеты и секущая грань-гипотенуза. Пришло время нарисовать еще одну картинку. 
Теорема Пифагора для прямоугольной пирамиды
На картинке изображена пирамида с вершиной в начале прямоугольных координат (пирамида как бы лежит на боку). Пирамида образована тремя взаимно-перпендикулярными векторами, отложенными из начала координат вдоль координатных осей. То есть каждая боковая грань пирамиды — это прямоугольный треугольник с прямым углом при начале координат. Концы векторов определяют секущую плоскость и образуют грань-основание пирамиды.
Теорема
Пусть есть прямоугольная пирамида, образованная тремя взаимно-перпендикулярными векторами , у которой площади граней-катетов равны —
, и площадь грани-гипотенузы —
. Тогда
Альтернативная формулировка: У четырехгранной пирамиды, у которой при одной из вершин все плоские углы прямые, сумма квадратов площадей боковых граней равна квадрату площади основания.
Разумеется, если обычная теорема Пифагора формулируется для длин сторон треугольников, то наша теорема формулируется для площадей сторон пирамиды. Доказать эту теорему в трех измерениях очень просто, если вы немного знаете векторную алгебру.
Доказательство
где .
Площадь представим как половину площади параллелограмма, построенного на векторах
и
Как известно, векторное произведение двух векторов — это вектор, длина которого численно равна площади параллелограмма, построенного на этих векторах.
Поэтому
Что и требовалось доказать!
ЭВРИКА!
Моему восторгу не было границ! Я буквально прыгал от счастья. Конечно, это не бог весть какая сложная теорема, и доказательство очень простое, но ведь сам. И до меня — никто! Я был в этом искренне убежден в течение около года. Попытки найти хоть какие-то свидетельства о том, что это уже известно и доказано терпели неудачу одна за другой, и я думал, что совершил открытие. Это непредаваемое чувство! Я хотел поделиться этой теоремой со всем миром. Говорил о ней друзьям, знакомым математикам, просто знакомым с техническим/математическим образованием и без. Никто не разделял моего восторга и энтузиазма. Всем было попросту безразлично. Будто бы я не придумал и доказал теорему, а просто в магазин за хлебом сходил. Ну и что тут такого? Вот уж действительно… Как говорится, «Как скучно мы живём! В нас пропал дух авантюризма, мы перестали лазить в окна к любимым женщинам, мы перестали делать большие хорошие глупости.» (из фильма «Ирония судьбы»).
Конечно, как у человека, профессионально занимающегося исследованиями, подобное в моей жизни уже случалось, и не раз. Но этот момент был самым ярким и самым запоминающимся. Я испытал полную гамму чувств, эмоций, переживаний первооткрывателя. От зарождения мысли, кристализации идеи, нахождения доказательства — до полного непонимания и даже неприятия, которое встретили мои идеи у моих друзей, знакомых и, как мне тогда казалось, у целого мира. Это было уникально! Я словно почувствовал себя в шкуре Галлилея, Коперника, Ньютона, Шредингера, Бора, Эйнштейна и многих многих других открывателей.
Послесловие
В жизни, все оказалось гораздо проще и прозаичнее. Я опоздал… Но на сколько! Всего-то навсего 18 лет! Под страшными продолжительными пытками и не с первого раза Гугл признался мне, что эта теорема была опубликована в 1996 году!
Вот ссылка на статью:
Статья опубликована издательством Техасского технического университета. Авторы, профессиональные математики, ввели терминологию (которая, кстати, во многом совпала с моей) и доказали также и обобщенную теорему справедливую для пространства любой размерности большей единицы. Что же произойдет в размерностях более высоких, чем 3? Все очень просто: вместо граней и площадей будут гиперповерхности и многомерные объемы. А утверждение, конечно, останется все тем же: сумма квадратов объемов боковых граней равна квадрату объема основания, — просто количество граней будет больше, а объем каждой из них станет равен половине произведения векторов-образующих. Вообразить это почти невозможно! Можно только, как говорят философы, помыслить!
Что удивительно, узнав о том, что такая теорема уже известна, я ничуть не расстроился. Где-то в глубине души я подозревал, что вполне возможно, я был не первый, и понимал, что нужно быть всегда к этому готовым. Но тот эмоциониальный опыт, который я получил, зажег во мне искру исследователя, которая, я уверен, теперь уже не угаснет никогда!
Эрудированный читатель в комментариях прислал ссылку
Теорема де Гуа
Выдержка из Википедии
В 1783 году теорема была представлена Парижской академии наук французским математиком Ж.-П. де Гуа, однако ранее она была известна Рене Декарту[3] и до него Иоганну Фульгаберу (англ.), который, вероятно, первым открыл её в 1622 году[4]. В более общем виде теорему сформулировал Шарль Тинсо (фр.) в докладе Парижской академии наук в 1774 году[4]
Так что я опоздал не на 18 лет, а как минимум на пару веков!
Источники
Читатели указали в комментариях несколько полезных ссылок. Вот эти и некоторые другие ссылки:





