Шестнадцатеричная система счисления

Шестнадцатеричный код ☑️ расшифровка системы счисления, как перевести шестнадцатеричное число в десятичное, как переводить из двоичной в шестнадцатеричную систему, примеры преобразований

Для чего нужна шестнадцатеричная система

Итак, шестнадцатеричная система счисления, как следует из названия, имеет в своём основании число 16. Почему так? Дело в том, что единица информации в информатике – это бит. Восемь бит образуют байт. Также информационной среде существует такое понятие, как машинное слово – это минимальная единица данных, представляющая собой шестнадцать бит, то есть два байта. Считается, что машинное слово – это минимальная величина разрядности регистров процессора, при которой можно работать с ЭВМ. Так вот, как мы знаем, компьютер работает на двоичном коде. Однако, если Вы когда-нибудь переводили числа из двоичной системы в десятичную, то замечали, что в ней бывает довольно много разрядов, особенно при переводе больших чисел, например, перевод числа 5132 в двоичной системе будет записано так:

Как можно увидеть, при переводе в двоичную систему этого числа у нас получилось аж 13 разрядов (с 0 до 12). Довольно муторно, а главное, занимает много места на письме и отнимает много времени для перевода. Именно для этого придумали восьмеричную и шестнадцатеричную системы счисления, для этого придумали и байты. Эти системы помогают сократить затраты на перевод чисел и привести их к более приятному визуальному виду. Если перевести то же число 5132 в восьмеричную систему счисления, то получится «более сокращённая версия» двоичного кода:

Как мы видим, количество символов сократилось, так как разрядность уменьшилась до 5 (с 0 до 4). Как можно уже понять, шестнадцатеричная система ещё сильнее сокращает разрядность (с 0 до 3) и ещё сильнее сжимает на письме переведённое число:

Человеку такой вид записи в любом случае удобнее, чем бесконечные нули и единицы.

Таким образом, шестнадцатеричная система используется довольно широко в современных информационных системах. Например, при помощи неё указываются коды цветовых схем, данная система используется для записи кодов ошибок, а также для программирования на языках низкого уровня типа Ассемблера, шестнадцатеричную систему зачастую используют для предоставления данных и адресов в малоразрядных ЭВМ.

Применение шестнадцатеричной системы счисления

Шестнадцатеричная система, как и восьмеричная активно применяется в компьютерных технологиях. При этом, запись чисел гораздо компактнее. В отличии от восьмеричной, которая за годы развития информатики — устарела, шестнадцатеричная — применяется в следующих областях:

Низкоуровневое программирование (к примеру, ассемблер).
Стандарт Юникод.
Шестнадцатеричный цвет (RGB).
Запись кодов ошибок.
Представление данных в малоразрядных ЭВМ.

Как перевести из десятичной системы в шестнадцатеричную

Выше мы уже немного затронули процесс перевода чисел. Теперь мы рассмотрим его подробнее и на примерах.

Но прежде чем начать, надо узнать одну очень важную особенность шестнадцатеричной системы.

Так как система имеет своим основанием число 16, то, следовательно, всего в этой системе имеется 16 цифр, но если первые десять цифр (0-9) вполне привычные для нас, то остальные имеют вид не совсем цифровой, но, тем не менее, являются цифрами, а именно значения A, B, C, D, E, F, которые соответствуют нашим привычным числам с 10 до 15. Все цифры шестнадцатеричной системы и их «аналоги» в десятичной записаны в таблице ниже.

Итак, допустим, у нас есть число 40 563 в десятичной системе счисления. Переведём его в шестнадцатеричную.

Сначала мы просто делим наше исходное число 40 563 на 16 в столбик. В частном у нас получилось 2 535, если умножить это число на 16, то получится 40 560, а в остатке 3. Эту тройку мы выделяем.

Теперь мы делим 2 535, и тоже на 16, и тоже абсолютно таким же образом. Частное – 158, 16*158 = 2 528, а в остатке 7. Остаток так же, как и в тот раз, выделяем.

Делим полученные частные до тех пор, пока они не станут меньше 16 , тогда деление заканчивается. Делим 158 на 16, и находим остаток от этого деления.

Остаток от деления – 14, а частное, полученное при делении 158 на 16 равно 9. Так как 9 меньше 16, то процесс вычислений закончен, а 9 также выделяется.

Процесс преобразования десятичного числа в шестнадцатеричное почти окончен. Для того, чтобы получить его, надо всего лишь выписать выделенные числа справа налево (т.е. в данном случае от девятки к тройке), НО, как мы писали выше, у шестнадцатеричной системы свой особый «алфавит» с 10 по 15. И как раз один из наших «остатков» (число 14) вписывается в этот диапазон, поэтому надо посмотреть в таблице, либо просто самостоятельно посчитать, что в шестнадцатеричной системе 14 будет буквой Е.

Итого весь процесс преобразования приведён на следующем изображении:

Таким образом мы научились переводить числа из десятичной системы в шестнадцатеричную. Теперь давайте попробуем сделать обратное преобразование, но уже с другим числом.

Двоичная система счисления ; основа мироздания.

Вы помните Даосский символ Инь и Янь? Он состоит из двух цветов, из двух понятий: чёрного и белого, мужского и женского, единицы и нуля. Согласно Даосской философии весь мир сформирован именно с помощью двух противоположных

и вместе с тем неразделимых понятий. Просто поражает гениальность древних мудрецов. С помощью единиц и нулей человек создаёт множество цифровых миров. Год от года они становятся всё более реалистичными. Интересно, догадывается

Позиционные системы в программировании

Наиболее востребованными в IT-сфере являются двоичный и шестнадцатеричный коды. Они применяются для перевода десятичной системы счисления, которая понятна человеку, в машинный язык. Двоичная состоит из двух переменных, которые принимают единичное (1) или нулевое (0) значения. Это очень просто реализовать в электронике и микросхемотехнике.

Микропроцессор персонального компьютера является микросхемой. Она состоит из множества транзисторов, способных кодировать 0 и 1. Схему соединения полупроводниковых приборов составляют так, чтобы они имели два состояния (открыт и закрыт). Кроме того, реализация двоичной системы может быть выполнена в любом устройстве, которое потребляет электрический ток. Наличие кодируется как 1, а отсутствие — 0.

Берутся также некоторые физические процессы: наличие света, сопротивления, намагниченности и так далее. С системой можно связать разные величины, которые имеют два состояния. Новичкам рекомендуется сначала полностью освоить перевод из десятичной системы счисления в двоичную и обратно. После этого следует приступить к изучению шестнадцатеричного кода, расшифровка которого существенно отличается.

Шестнадцатеричная система счисления.

В шестнадцатеричной системе счисления одним символом отображаются числа от нуля до шестнадцати. Чтобы не сочинять новых отображений цифр, решили использовать буквы латинского алфавита: A, B, C, D, E, F.

Для большей понятности — внизу приведена таблица соответствия цифр трём системам счисления.

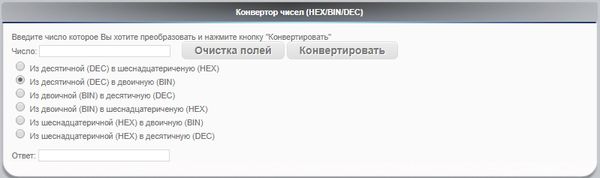
Запоминать соответствия цифр нет необходимости. В состав Windows любой версии входит программа «калькулятор» — calc.exe. Запустите её, переключитесь в программистский вид (Вид->Программист или Alt+3) и да пребудет с вами сила!

Калькулятор программиста: HEX, DEC, OCT, BIN.

Как перевести шестнадцатеричный код в другую систему?

Перевод из шестнадцатеричной системы в десятичную. Для совершения операции перевода из шестнадцатеричной системы в десятичную, требуется представить исходное число как сумму произведений цифр в разрядах шестнадцатеричного числа на степень основания.

Двоичная СС

шестнадцатеричная СС

Например, требуется выполнить перевод шестнадцатеричного числа A14: в нём три цифры. Используя правило, запишем его в виде суммы степеней с основанием 16:

A14₁₆ = 10•16 2 + 1•16 1 + 4•16 = 10•256 + 1•16 + 4•1 = 2560 + 16 + 4 = 2580₁₀

Вычитание числа из строки и прибавление к строкам числа

В статье «Анализ вредоносной программы под Linux: плохое самодельное шифрование» рассматривается шифрование, которое основано на прибавлении или вычитании числа к символу строки (на основе позиции символов). Как я думаю вы уже поняли, используется аналогичный приём: берётся ASCII код символа и из этого числа делается вычитание или находиться сумма с ним, а затем полученное число опять переводят в ASCII символ.

Три системы счисления ; практическое использование.

Три системы счисления широко используются в программировании и отладке уже созданных программ.

Шестнадцатеричный (HEX) код удобен для современных процессоров, которые фактически развиваются на основе 16-ти разрядного процессора для персональных компьютеров Intel i8086. В исходных текстах программ практически всех языков программирования цифра обозначает по умолчанию число в десятичной системе счисления (DEC).

Десятичная система счисления более удобна (хотя и не всегда) при написании кода программ, шестнадцатеричная — неотъемлемая часть отладки, взлома, реверсивного программирования.

Двоичная система счисления (BIN) используется в основном при расстановке флагов определённых стилей объектов Windows (стили окон), но об этом попозже. Рассматривая 16 битное число в виде двоичного мы получаем великолепную возможность получить крохотный по размеру набор 16 флагов, где 1 — флаг установлен 0 — флаг снят (например, шестнадцатеричное число 4 000 соответствует двоичному 0100 0000 0000 0000 — установлен второй флаг, остальные сняты; шестнадцатеричное число 3000 соответствует двоичному числу 0011 0000 0000 0000 — установлены третий и четвёртый флаги, остальные сняты ).

Если мы хотим обозначить принадлежность числа к 16-тиричной системе счисления, то: 1. Ассемблер — добавляем к числу постфикс h (H), например: 100h = 256, 10H=16. Иногда для понимания того, что мы имеем дело с числом, в качестве префикса ставят 0 (ноль). 2. Си (С++) к числу добавляется суффикс 0x (0X).

Например: 0x100 = 100h = 0100h = 256, 0x10 = 10H = 010H = 16

ASCII и HTML

Если в HTML коде перед десятичным кодом ASCII символа поставить &#, то веб-браузер отобразит этот символ.

К примеру, если использовать &#39, то веб-браузер покажет ‘ (одинарную кавычку). Некоторые преобразователи строк внутри веб-приложения также могут конвертировать написание символов &#XX в их ASCII представления. Поэтому безобидная запись &#39 внутри веб-приложения может превратиться в одинарную кавычку, которая может нарушить SQL запрос.

Аналогично можно использовать &#x, после которой нужно указать код символа в шестнадцатеричной системе, например, &#x27 также покажет кавычку. Для разделения символов друг от друга, используйте точку с запятой, например, ‘hi’

Многие программы понимают шестнадцатеричную запись, правда вид записи может различаться от конкретной программы и языка программирования.

В JavaScript шестнадцатеричные строки записываются в виде экранированной последовательности:

Можно записать код символов в восьмеричной системе счисления:

Аналогично Bash понимает такие строки:

И PHP их обрабатывает верно:

Шестнадцатеричный формат

Осуществить конвертацию из десятичного в шестнадцатеричный код (HEX — hexadecimal) можно только с использованием программ. Ручной метод основан на двойной конвертации. Для его реализации нужно перевести число, записанное в десятичной системе, в двоичный код, а затем в шестнадцатеричный.

Основанием является целочисленное значение, равное 16. Система состоит из арабских цифр от 0 до 9, а также букв, обозначающих конкретные значения: А = 10, В = 11, С = 12, D = 13, Е = 14 и F = 15. В автоматизированном режиме можно воспользоваться переводчиком шестнадцатеричного кода.

Способы записи

Существует несколько форм записи числа, представленного в HEX. Математическая форма выглядит таким образом: [DF5]<16>. Можно также найти запись, в которой вместо <16>стоит нижний индекс. Она применяется в информатике.

Запись отличается в языках программирования, поскольку у каждого из них различный синтаксис и правила написания кода. Основные формы представления HEX следующие:

В С, С++ и похожих применяется префикс «0х».
В Ассемблере после числа ставится латинская буква «h».
В Pascal, Delfi, Basic используется символ «$».
В HTML и CSS — «#».
В Python — «0х».

Распространенная ошибка новичков заключается в том, что они неверно указывают HEX-числа. В результате компилятор языка выдает ошибку. Программисты рекомендуют основательно изучить синтаксис языка перед написанием приложений.

Алгоритм конвертации

Перевод в шестнадцатеричный код рекомендуется осуществлять с помощью специальных приложений (конвертеров кода). Если же их нет под рукой, то специалисты рекомендуют использовать специальный алгоритм:

Выполнить конвертацию десятичной формы записи в двоичную по любому алгоритму.
Распределить знаки на тетрады (по 4 штуки или четверичные группы). Если в какой-то группе их количество меньше 4, то дописывается в начале 0.
Записать значения для каждой тетрады.
Проверить результат.

Операции умножения, сложения, вычитания и деления сложны.

Они осуществляются только с помощью специальных программ или онлайн-сервисов.

Не следует путать четверичные с троичными группами, которые используются в восьмеричном коде.

Например, нужно перевести 118 в HEX-код.

Для этого следует воспользоваться описанным алгоритмом:

Степенной метод, описанный выше: [118] <10>= [1110110]<2>.
Распределение символов на тетрады (в старшем разряде нужно дописать 0): 0111 0110.
Первое значение: 0 + 2 2 + 2 1 + 2 = 0 + 4 + 2 + 1 = [7]<16>.
Второе: 0 + 2 2 + 2 1 + 0 = [6]<16>.
Результат: [76]<16>.

В некоторых случаях нужно использовать буквы. Например, для перевода числа [11110111] <2>в HEX-код нужно также воспользоваться алгоритмом, разбивая его на тетрады следующим образом: 1111 0111. Первая группа равна 2 3 + 2 2 + 2 1 + 2 = [15] <10>= F<16>, а вторая — 0 + 2 2 + 2 1 + 2 = 7. Результирующая запись имеет такой вид: [11110111] <2>= [F7]<16>.

Таким образом, HEX-код получил широкое применение в IT-сфере, поскольку он очень удобен для записи массивов информации. Однако для его конвертации в ручном режиме нужно изучить двоичную систему счисления, а также основные алгоритмы преобразования.

Лучшие Hex редакторы, калькуляторы и конвертеры

У людей сложилось мнение, что работать с hex редакторами могут лишь профессионалы своего дела и программисты, а для обывателя это нечто ненужное и непонятное. На деле же это удобный инструмент, который определённо пригодится геймерам и простым пользователям, если необходимо устранить ошибку или баг в утилите. По своей сути – редактор является декодером 16-ричного кода. Мы с вами пользуемся для написания чисел 10-ричным, машина для кодирования всей информации использует 2-ичный код, а затем это всё конвертируется в 16-ричный, чтобы пользователю было проще разбираться. На деле редакторы скорее нужны именно новичкам, ведь профессионалы используют мультифункциональные утилиты с возможностью применения сразу нескольких парадигм, если те необходимы им для программирования. Давайте разберёмся, какие калькуляторы и конверторы лучше всего выбирать.

Hex Editor Neo

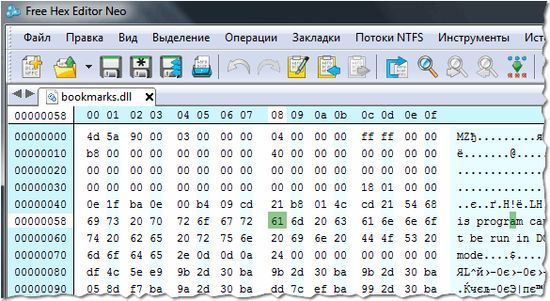
Простейший и самый популярный hex редактор в мире, притом с возможностью конвертации кода в другие системы кодировки, а также чтения бинарных файлов системы. Весь функционал Hex Editor Neo заключается в открытие файлов, произведение некоторых изменений и сохранение в том же или другом формате, по желанию пользователя. Однако присутствует одно удобство – история изменений, сохраняющаяся даже после закрытия утилиты. Таки, и не придётся вновь доходить до каких-то своих решений. Они будут м образом, вы можете завтра вернуться к той части кода, что сегодня не успели завершить прямо перед вами на экране. Такой Хекс редактор удобен новичкам и профессионалам.

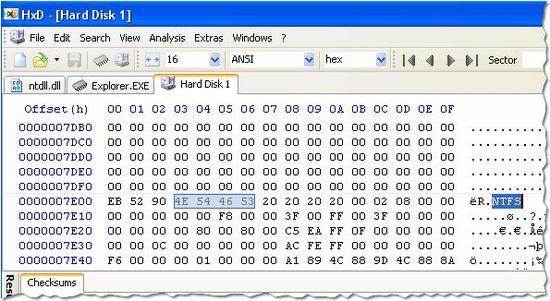
HxD Hex Editor

Бесплатный, но всё ещё достаточно мощный редактор для бинарных файлов поддерживающий основные кодировки, вроде ANSI или ASCII, зачастую используется как дополнение к более функциональным калькуляторам и конверторам. Воспринимает файлы без ограничения размеров, а главное – позволяет изменять оперативную память, сразу же записывая любые нововведения на жёсткий диск. А удобный и эргономичный интерфейс, продуманный создателями, лишний раз упрощает работу пользователя. В HxD Hex Editor нет классического нагромождения инструментов и всё устроено за счёт простой системы шторок, уже за это можно скачать hex редактор.

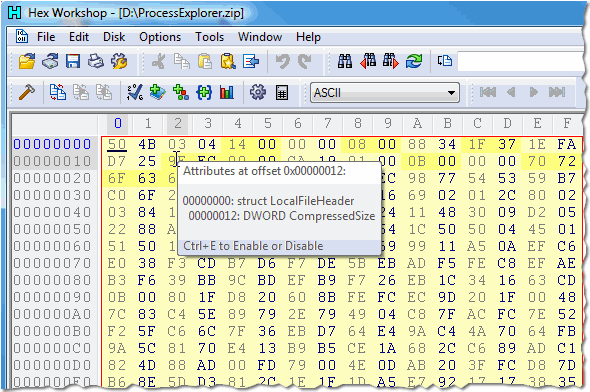
Hex Workshop

Один из простых редакторов, подходящих для компьютеров с любым железом. Именно его небольшая требовательность к ресурсам системы и удобный интерфейс, пусть и с некоторым наплывом объектного дизайна Майкрософт начала 2000-х, сделала программу столь популярной в качестве переносного редактора. Если вам необходимо подгрузить утилиту на флешку, а затем уже на месте разобраться с проблемой в коде, то лучшего решения просто не найти, ведь приложение имеет в том числе и портативную версию с ещё меньшими системными требованиями. А также имеется мобильная версия, и вы можете hex workshop скачать прямо на свой смартфон.

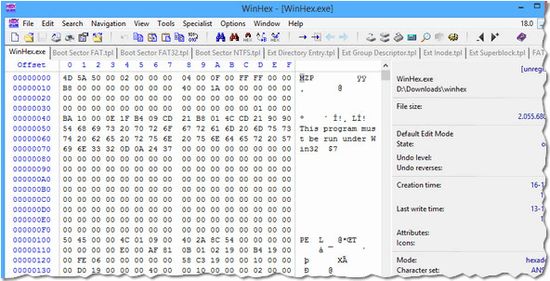
WinHex

Данный hex редактор условно-бесплатен, что значит, за основную часть функционала вам придётся заплатить. Однако, базовое редактирование файлов нескольких форматов и конвертирование из одной системы кодировки в другую – доступны без оплаты. Что позволяет опробовать все прелести редактора абсолютно бесплатно, а уже затем решить, покупать ли его. Основное преимущество – сборная солянка функционала, настолько богатой среды для работы вы больше нигде не найдёте.

HexCmp

Это hex editor скачать стоит в том случае, если вам часто приходится сравнивать несколько файлов между собой, дабы найти ошибку или изменение, внесённое вашим коллегой. Помимо удобного отображения несовпадающих частей, утилита предоставляет также простой функционал обычного редактора и конвертора, а также базовый набор джентльмена в такого рода программах.

Hex редактор онлайн

Если вам необходимо быстро внести пару изменений в hex код и при этом не заморачиваться лишний раз с установкой приложений, то подойдут и онлайн-редакторы. Однако учитывайте, что их функционал крайне скуден. Вот ссылок на подобные онлайн решения:

Конвертер Hex в DEC, BIN и наоборот

В качестве конвертера hex to dec, hex to bin подойдёт любая из вышеописанных утилит. Достаточно загрузить в них файл и выбрать пункт «сохранить как», а там подобрать подходящий формат, и утилита сама преобразует все данные в нужное расширение, после чего вы сможете открыть файл уже подходящего типа.

Также есть и специализированное решение:

Конвертер Hex в ASCII Text

Конвертер hex to text или его ещё называют hex decoder необходим для перевода 16-ричного кода в нормальный текст, и зачастую используется лишь новичками, так как профессионалы применяют утилиты с параллельным переводом. Подобный функционал имеется во всех описанных выше продуктах.

Hex калькулятор онлайн

Подобный калькулятор онлайн бывает крайне полезен, когда вам нужно быстро совершить расчёты в 16-ной системе исчисления. Вот ссылка на удобный и хороший онлайн Hex калькультор:

Вывод

Выбирайте любую описанную утилиту по желанию или пользуйтесь онлайн-аналогами, если необходимость возникает не часто. hex editor neo – станет лучшим выбором как для новичков, так и для профессионалов.

Программирование на C, C# и Java

Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы

ОСТОРОЖНО МОШЕННИКИ! В последнее время в социальных сетях участились случаи предложения помощи в написании программ от лиц, прикрывающихся сайтом vscode.ru. Мы никогда не пишем первыми и не размещаем никакие материалы в посторонних группах ВК. Для связи с нами используйте исключительно эти контакты: vscoderu@yandex.ru, https://vk.com/vscode

Шестнадцатеричная система счисления

Системы счисления – одна из самых главных основ информатики. Практически ни в одной школе и ни в одном университете не пропускают данную тему, но зачастую именно с переводом шестнадцатеричной системы у многих возникают проблемы, хотя это не такая уж сложная задача, и её перевод практически не отличается от других систем счисления.

Давайте рассмотрим эту систему поподробнее.

Для чего нужна шестнадцатеричная система

Итак, шестнадцатеричная система счисления, как следует из названия, имеет в своём основании число 16. Почему так? Дело в том, что единица информации в информатике – это бит. Восемь бит образуют байт. Также информационной среде существует такое понятие, как машинное слово – это минимальная единица данных, представляющая собой шестнадцать бит, то есть два байта. Считается, что машинное слово – это минимальная величина разрядности регистров процессора, при которой можно работать с ЭВМ.
Так вот, как мы знаем, компьютер работает на двоичном коде. Однако, если Вы когда-нибудь переводили числа из двоичной системы в десятичную, то замечали, что в ней бывает довольно много разрядов, особенно при переводе больших чисел, например, перевод числа 5132 в двоичной системе будет записано так:

Как можно увидеть, при переводе в двоичную систему этого числа у нас получилось аж 13 разрядов (с 0 до 12). Довольно муторно, а главное, занимает много места на письме и отнимает много времени для перевода.
Именно для этого придумали восьмеричную и шестнадцатеричную системы счисления, для этого придумали и байты. Эти системы помогают сократить затраты на перевод чисел и привести их к более приятному визуальному виду.
Если перевести то же число 5132 в восьмеричную систему счисления, то получится «более сокращённая версия» двоичного кода:

Как мы видим, количество символов сократилось, так как разрядность уменьшилась до 5 (с 0 до 4).
Как можно уже понять, шестнадцатеричная система ещё сильнее сокращает разрядность (с 0 до 3) и ещё сильнее сжимает на письме переведённое число:

Человеку такой вид записи в любом случае удобнее, чем бесконечные нули и единицы.

Как перевести из десятичной системы в шестнадцатеричную

Выше мы уже немного затронули процесс перевода чисел. Теперь мы рассмотрим его подробнее и на примерах.

Но прежде чем начать, надо узнать одну очень важную особенность шестнадцатеричной системы.

Итак, допустим, у нас есть число 40 563 в десятичной системе счисления. Переведём его в шестнадцатеричную.

Сначала мы просто делим наше исходное число 40 563 на 16 в столбик. В частном у нас получилось 2 535, если умножить это число на 16, то получится 40 560, а в остатке 3. Эту тройку мы выделяем.

Теперь мы делим 2 535, и тоже на 16, и тоже абсолютно таким же образом. Частное – 158, 16*158 = 2 528, а в остатке 7. Остаток так же, как и в тот раз, выделяем.

Делим полученные частные до тех пор, пока они не станут меньше 16 , тогда деление заканчивается. Делим 158 на 16, и находим остаток от этого деления.

Процесс преобразования десятичного числа в шестнадцатеричное почти окончен. Для того, чтобы получить его, надо всего лишь выписать выделенные числа справа налево (т.е. в данном случае от девятки к тройке), НО, как мы писали выше, у шестнадцатеричной системы свой особый «алфавит» с 10 по 15. И как раз один из наших «остатков» (число 14) вписывается в этот диапазон, поэтому надо посмотреть в таблице, либо просто самостоятельно посчитать, что в шестнадцатеричной системе 14 будет буквой Е.

Итого весь процесс преобразования приведён на следующем изображении:

Как перевести из шестнадцатеричной системы в десятичную

Перевести шестнадцатеричное число в привычное нам десятичное также совсем не сложно, более того, мы уже делали это в самом начале статьи, когда сравнивали двоичную, восьмеричную и шестнадцатеричную системы счислений, теперь же разберём этот процесс более подробно.
Давайте сразу приступим к примеру и переведём шестнадцатеричное число 1C3B3 в десятичную систему.
По сути, процесс перевода можно разделить на 2 этапа:

Мы справа налево отделяем от числа все цифры и умножаем каждую из них на 16, и всё это складываем:

Также обязательно необходимо перевести буквенные обозначения шестнадцатеричной системы в числовые, чтобы можно было посчитать их в десятичном виде, то есть, для данного случая, перевести B в 11 и C в 12.

После того, как мы сделали этот шаг, нам необходимо пронумеровать разряды чисел. Делается это просто – мы приписываем ко всем числам 16, на которые мы умножали наши исходные цифры, степени, начиная с нулевой:

Теперь нам остаётся только перемножить и сложить всё это:

Таким образом, мы превратили шестнадцатеричное число 1C3B3 в десятичное число 115 635.

Как видите, ничего сложного. Также у нас на сайте имеется статья, описывающая процесс перевода чисел из шестнадцатеричной системы в двоичную.
Спасибо за прочтение!

От 0 до F: шестнадцатеричные числа

Шестнадцатеричные данные. Это информация внутри вашего компьютера. Но что на самом деле такое шестнадцатеричное число? Что означают странные и непривычно выглядящие шестнадцатеричные числа? Как появилось шестнадцатеричное число? Узнайте больше о шестнадцатеричном формате сегодня.

Что такое шестнадцатеричный?

Шестнадцатеричная система счисления использует шестнадцать символов (от 0 до 9 и от A до F) для образования и представления любого числа. Шестнадцатеричная система используется в компьютерах и калькуляторах. Слово «шестнадцатеричный» часто сокращается до hex, а hex происходит от слова hexagon, то есть шестиугольник, шесть. На английском языке слово «шестнадцатеричный» записывается как hexadecimal и вы можете сразу увидеть логику названия hexa..decimal, поскольку decimal означает (10), а hexa означает 6 (A-F, 6 символов).

Компьютеры часто используют шестнадцатеричные числа в своих внутренних вычислительных системах. Существует прямая связь между двоичными и восьмеричными числами и шестнадцатеричными числами. Чтобы узнать больше о шестнадцатеричной системе счисления с 16 основанием (16 основных элементов, 16 основных чисел), нам нужно немного отступить и сначала изучить двоичную и восьмеричную системы. Если вы раньше не слышали эти термины, не волнуйтесь, это далеко не так сложно, как кажется.

Что такое двоичный?

Двоичные числа, особенно двоичная система счисления, является одной из самых, если не самых простых систем счисления на планете. В двоичном формате есть только два возможных числа (отсюда и термин двоичный, т.е. состоящий из двух вещей), и это ноль (0) и единица (1). Хотя мы используем ноль и единицу для представления двух возможных чисел в этой системе, пожалуйста, поймите, что это всего лишь выбор — точно так же, как я бы использовал буквы латинского алфавита A-Z для представления слов на английском языке или китайских символов для представления слов на китайском языке.

Таким образом, мы могли бы создать двоичный код, в котором использовались бы не ноль и единица, а A и B или $ и %, это мало что поменяло бы. Однако здесь есть небольшая интересная оговорка, которая на самом деле упрощает использование нуля и единицы для двоичных файлов; компьютеры понимают только одно: есть электрическое напряжение или его нет. Подумайте об этом как о единице или нуле: единица означает +5В (5 Вольт), а ноль означает 0В (0 Вольт). Возможно, это немного упрощено, но это хорошая аналогия того, что происходит внутри компьютера. Таким образом, у нас есть двоичное состояние.

Так как же считать в двоичной системе счисления с двумя основными числами? Все мы знаем, как считать в десятичной системе счисления (десятичная система счисления, которую мы используем каждый день для всех наших выражений количества и т. д.), 0… 1… 2… 3…, но как мы это делаем, если мы даже не можем выйти за рамки 1 к 2? Что произойдёт, когда мы дойдём до 9 и нам нужно будет найти следующее число? Мы добавляем единицу впереди (первая цифра в 10) и сбрасываем нашу вторичную позицию на 0. Мы продолжаем делать это, чтобы считать до 99, а затем делаем то же самое, хотя на этот раз мы сбрасываем две позиции.

Мы можем использовать тот же метод в нашем 2-базовом двоичном вычислении, и это именно то, что мы делаем и как мы считаем. Начнём: 0… 1… 10… 11… 100… 101… 110… 111… 1000…. Не сложно, правда? Если вы ещё не знали, как считать в двоичном формате, поздравляем, теперь вы знаете, как это сделать! В наши дни этому навыку обучают в средней школе. Перейдём к восьмеричному.

Что такое восьмеричный?

До сих пор мы обнаружили, что десятичное число также может быть обозначена как число с основанием 10, потому что оно имеет 10 различных символов для выражения чисел (от 0 до 9), а в число с основанием 2 только ноль и один. Теперь мы представим восьмеричную, ещё одну компьютерно-ориентированную систему счисления, которая имеет 8 возможных символов. Как вы уже догадались, от нуля (0) до семи (7). Вы можете начать понимать, почему существуют такие системы счисления: добро пожаловать в степень двойки: 2 (двоичная) > 4 (полбайта) > 8 (восьмеричная, один байт) > 16 (шестнадцатеричная).

Так что же такое байт? Байт состоит из восьми битов (обычно визуально отображается как 2 набора по 4 бита, хотя для компьютера это просто 8 бит в строке), образующих один байт. Например, 0110 1100 — это действительный байт, состоящий из 8 бит. Это число можно преобразовать в восьмеричное (154), шестнадцатеричное (6C) и десятичное (108). Обратите внимание на то, что чем выше номер основания числа, тем короче его запись, например, 6C в шестнадцатеричной системе записывается как 154 в восьмеричной системе счисления. В двоичной системе счисления запись этого числа будет ещё длиннее.

Байт часто используется для хранения простых буквенно-цифровых символов. Например, буква «A» записывается в двоичном формате как 0100 0001. Обратите внимание, что максимальное значение в байте (например, 1111 1111) равно 255, и, таким образом, существует только 256 возможных комбинаций (+1, поскольку 0 также является возможной опцией) — это все возможные комбинации, которые можно сделать с помощью одного байта. Таким образом, наш ограниченный диапазон от A до Z, даже включая цифры 0-9 и строчные буквы a-z, все вместе легко умещается в один байт, и мы даже можем представить некоторые другие символы, такие как «@» и «!».

Однако, когда речь идёт, например, о китайском с его множеством разных символов, нам может потребоваться два или более байта для хранения наших отдельных символов, то есть многобайтовые символы.

Возвращаясь к восьмеричной системе счисления, как считать восьмеричные числа? Как вы уже догадались, всё происходит как в десятичной и двоичной системах счисления: тот же метод, который мы уже видели, после каждого раунда дописывается ещё одна цифра, а предыдущие цифры сбрасываются на ноль. Только нужно помнить о том, что в восьмеричной системе счисления максимальной (последней) цифрой является 7. Посчитаем вместе: 0… 1… 2… 3… 4… 5… 6… 7… 10… 11… — выглядит немного странно, не так ли? Это потому, что наш разум так настроен думать о 10, ну, как о «10». Но 10 в восьмеричной системе счисления равно 8 в десятичной. Сбивает с толку? Для нас, простых людей, да, восьмеричная система счисления с основанием числа 8 может сбивать с толку. Для компьютера это не проблема.

Подсчёт в шестнадцатеричной системе счисления

Это возвращает нас к счёту в нашей системе счисления с основанием 16: шестнадцатеричной. Теперь мы знаем шаги, которым нужно следовать, и можем сосчитать (пропустим подсчёт от нуля до девяти): 0… пропуск до… 9… A… B… C… D… E… F… 10… 11…. Теперь мы понимаем, что 10 в шестнадцатеричной системе счисления, как и в восьмеричной, имеет другое значение, чем то, что мы можем подумать (исходя из нашей привычки пользоваться десятичной системой счисления), поскольку мы ведём счёт в шестнадцатеричной системе счисления, которая соответствует основанию равному 16, а не десятичной системе счисления, в которой основание равно 10. Число 10 в шестнадцатеричном формате на самом деле равно 16 в десятичном!

Примечательно, что шестнадцатеричный формат, именно потому, что он состоит из 16 оснований, позволяет нам хранить весь байт в двух символах! Мы не можем сделать это с десятичным числом, поскольку двоичное значение 1111 1111 (т.е. 1111111 для компьютера) равно 255 в десятичном формате. Однако в шестнадцатеричном формате оно может быть представлено как FF, который в десятичном виде равен 255. Также обратите внимание, что полбайта, 4 бита, можно сохранить в одном шестнадцатеричном символе.

Подведение итогов

Мы надеемся, что вам понравилось это введение в шестнадцатеричную, нашу 16-символьную или 16-базовую числовую систему, а также в двоичную систему счисления с двумя базовыми числами и восьмеричную систему счисления с основанием числа 8. Мы также узнали, как мы ведём ежедневный счёт в десятичной системе счисления, в нашей очень знакомой десятичной системе счисления используются числа от 0 до 9.

Мы также увидели, что символы, которые мы используем для представления двоичных, восьмеричных, шестнадцатеричных и даже десятичных значений, — это всего лишь символы, которые человечество выбрало для представления этих различных систем счисления. Мы могли бы легко выбрать другие представления для других числовых систем, но повторное использование тех же чисел кажется знакомым и имеет некоторый смысл, особенно в случае двоичной системы «напряжение» и «отсутствие напряжение», представлены нулём и единицей.

MS-DOS и TASM 2.0. Часть 6. Системы счисления.

Три системы счисления.

Практическое программирование на ассемблере требует понимания системы счисления. Систем счисления существует бесконечное множество. Наиболее знакомая для нас — десятичная система счисления. Римская нумерация циферблата часов демонстрирует нам двенадцатеричную систему счисления. Программистам на ассемблере необходимо освоить три системы счисления : десятичную, двоичную и шестнадцатеричную.

Машина «думает» байтами. Байт состоит из 8 бит. Бит может содержать одно значение: 0 или 1. Так что в принципе, неплохо иметь представление и о восьмеричной системе счисления.Однако машинный код отображается в различных редакторах в виде шестнадцатеричного значения — оно более удобно для восприятия, так что всё же остановимся на трёх обязательно необходимых программисту системах счисления.

Двоичная система счисления — основа мироздания.

ли герой компьютерной игры, что весь его мир состоит всего из двух цифр или это только мы такие прозорливые :)?

Десятичная система счисления.

Двоичная система счисления аппретирует только двумя цифрами: Единицей

и Нулём (Инь и Янь). Привычная для нас система счисления — десятеричная. Если все цифры до десяти состоят из различных одиночных символов (от нуля до девятки), то десять отображается уже двумя символами — единицей и нулём, расположенных

в определённой последовательности (10 — единица перед нулём).

Шестнадцатеричная система счисления.

В шестнадцатеричной системе счисления одним символом отображаются числа от нуля до шестнадцати. Чтобы не сочинять новых отображений цифр,
решили использовать буквы латинского алфавита: A, B, C, D, E, F.

Для большей понятности — внизу приведена таблица соответствия цифр трём системам счисления.

Калькулятор программиста: HEX, DEC, OCT, BIN.

Три системы счисления — практическое использование.

Три системы счисления широко используются в программировании и отладке уже созданных программ.

Если мы хотим обозначить принадлежность числа к 16-тиричной системе счисления, то:
1. Ассемблер — добавляем к числу постфикс h (H), например: 100h = 256, 10H=16. Иногда для понимания того, что мы имеем дело с числом, в качестве префикса ставят 0 (ноль).
2. Си (С++) к числу добавляется суффикс 0x (0X).

Например: 0x100 = 100h = 0100h = 256, 0x10 = 10H = 010H = 16

Хакерский редактор Hacker Viewer (Hiew) .

Для визуального восприятия шестнадцатеричного кода воспользуемся замечательным простым, но достаточно функциональным DOS редактором Hacker Viewer (Hiew). Вы найдёте его в папке D:UTILSHIEW (я надеюсь, что наш архив программ DOS-1.rar уже скачан и DOSBox установлен и запущен).

Запускаем HIEW (Hacker Viewer).

Инструкцию по пользованию Hiew для хакеров от Криса Касперского вы найдёте в папочке readme. Пользоваться редактором просто и удобно.

Откроем с помощью Hiew нашу программу PRG.COM (выбор файлов — F9). При помощи F4 выбираем режим отображения информации HEX (как вы уже знаете, шестнадцатеричный режим). Можете с помощью F4 или Enter по переключаться между режимами отображения.

Переключение режимов отображения в Hacker Viewer.

Обратите внимание на положение Decode (декодирование). Вам это ни о чём не говорит? Да, да, да в Hiew имеется встроенный дизассемблер и даже ассемблер! Можно внести изменения в ассемблерный код, не выходя из редактора и сохранить изменения.
Исполняемый файл останется рабочим — гениальная программа с поразительными возможностями для своего времени!

Подобное отображение HEX системы счисления вы увидите практически во всех отладочных программах и просмотрщиках файлов.
Перемещайте курсор с помощью клавиш стрелок на клавиатуре. Вверху вы заметите изменение цифры указателя (pointer).

Наша первая программа в шестнадцатеричном виде.

Указатель является одним из основополагающих понятий в системе программирования. Основы понимания работы с указателем рассмотрим попозже.

Добавить комментарий Отменить ответ

Для отправки комментария вам необходимо авторизоваться.

Конвертер величин

x
TranslatorsCafe.com
Онлайн-конвертеры единиц измерения
Популярные
Механика
Теплота
Жидкости
Звук
Свет
Электротехника
Магнетизм
Радиация
Другие
Калькуляторы
Russian (Russia)

Конвертер чисел в различных системах счисления.

Оптическая сила в диоптриях и увеличение линзы

Подробнее о числах

Общие сведения

Число — это абстрактное математическое понятие обозначающее количество. Числа используются для счета. Числа использовались человеком с древнейших времен, вначале в виде счетных палочек или зарубок и черточек на дереве и кости, а потом и в виде более абстрактных систем. Существует много способов выражения чисел и работы с ними; некоторые из них приведены ниже. Системы счисления эволюционировали на протяжении многих веков и не все из них используются по сей день.

Различные способы представления чисел

Ученые считают, что понятие числа возникло в разных культурах независимо. Символы для обозначения цифр в письменном виде также возникли в каждой культуре отдельно, но постепенно, с развитием торговли, люди начали обмениваться идеями и заимствовать друг у друга принципы счисления или написания чисел. Поэтому те системы счисления, которыми мы сейчас пользуемся, создавались коллективно многими народами.

Арабские цифры

Арабская система счисления — одна из самых широко используемых систем счисления. Она была заимствована из Индии и доработана персидскими и арабскими математиками. В русском языке эта система называется в основном «арабской», но на других языках, например английском, она чаще называется «индо-арабской». В средние века, особенно ближе к середине и концу этого периода, торговля распространилась по всему миру, и купцы стали привозить в другие страны не только товары, но и сведения о науках, таких как математика. Благодаря этому арабские цифры начали использовать в Европе, сначала в монастырях, а позже и в светском обществе. Папа римский Сильвестр II одним из первых стал использовать и распространять арабские цифры взамен римских, познакомившись с ними благодаря связям с арабскими государствами на территории нынешней Испании. Европейские ученые приспособили и частично изменили написание цифр, и арабская система счисления получила широкое применение не только во всей Европе, но и по всему миру благодаря торговле и во время колонизации других континентов. Арабская система — десятичная, то есть с основанием 10 и с использованием десяти цифр, которыми можно выразить все возможные числа.

Десять — одно из наиболее широко используемых чисел в системах счета, и десятичная система распространена во многих странах. Это связано с тем, что издревле люди пользовались десятью пальцами на руках для счета. До сих пор люди, которые учатся считать или хотят проиллюстрировать пример, связанный со счетом, используют пальцы. Существуют даже такие выражения как «считать на пальцах». В некоторых культурах для счета использовали также и пальцы ног, костяшки пальцев, и даже пространство между пальцами. Интересно, что во многих языках слово, обозначающее пальцы и цифры — одно и то же. Например, в английском, это слово — «digit» (произносится как «диджит»).

Римские цифры

Римские цифры использовались в Древнем Риме и Европе примерно до четырнадцатого столетия. Их до сих пор используют в некоторых контекстах, например на циферблатах часов, в именах Папы Римского, в названиях повторяющихся событий, например, олимпийских игр, и так далее. Римская система счисления использует семь букв латинского алфавита для обозначения всех возможных комбинаций чисел:

I	1
V	5
X	10
L	50
C	100
D	500
M	1000

Порядок написания цифр важен потому, что большее число слева от меньшего значит, что оба числа необходимо сложить, в то время как меньшее число слева от большего следует вычесть из большего числа. Например, XI равняется одиннадцати, а IX — это 9. Это правило действует только для чисел: IV, IX, XL, XC, CD и CM. В некоторых случаях эти правила не соблюдаются, и числа пишутся в ряд, например XXXXX.

Системы счисления в других культурах

Во многих культурах использовались системы счисления, похожие на римскую и арабскую. Например, в кириллической системе счисления цифры от одного до девяти, десять, и кратные ста писались буквами кириллицы. Также существовал специальный знак, похожий на тильду «

», который писали над такими цифрами, чтобы показать, что это не буквы. Существовала похожая система и с использованием глаголицы. В еврейской системе счисления буквами еврейского алфавита записывали числа от одного до десяти, кратные десяти, сто, двести, триста, и четыреста. Остальные числа писали как сумму или произведение. Греческая система счисления также похожа на все, приведенные выше.

В некоторых культурах системы счисления были проще. Например, вавилонские цифры можно было записать с помощью двух клинописных знаков, обозначавших единицу (похожего на большую букву «Т») и десять (похожего на букву «С»). Так, например, 32 можно записать как «СССТТ», используя соответствующие знаки. Египетская система счисления похожа, только в ней существовали также символы для нуля, сотни, тысячи, десяти тысяч, ста тысяч и миллиона, а также были специальные знаки для записи дробей. Цифры майя записывались с помощью знаков, обозначавших ноль, единицу и пятерку. Числа выше девятнадцати также имели своеобразное написание. В них использовались знаки для одного и пяти, но с другим расположением, чтобы показать, что значение этих цифр — другое.

Единичная система счисления

В единичной или унарной системе счисления используется только один знак, обозначающий единицу. Каждое число записывается с помощью таких знаков, количество которых равно этому числу. Например, если такой знак — буква «А», то число пять можно записать как «ААААА». Унарная система часто используется учителями, которые учат детей считать, потому что она помогает детям понять зависимость между количеством предметов, например счетных палочек или карандашей, и более абстрактного понятия числа. Часто унарную систему используют во время игр, чтобы записывать очки, набранные командами, или для счета дней или предметов. Причем метод записи в разных культурах отличается. Например, во многих странах, где принят латинский алфавит, чаще используются черточки. Обычно четыре вертикальные черточки перечеркивают горизонтальной или диагональной, и продолжают счет с новой группы черточек. В примере А) на рисунке счет доходит до четырех, эти черточки перечеркивают пятой, дальше добавляют еще пять черточек, и опять начинают новый ряд. Так, счет доходит до двенадцати. В странах, где в языке используют или использовали китайские иероглифы, люди обычно рисуют не четыре черточки, перечеркнутые пятой, а специальный иероглиф из пяти штрихов. Последовательность этих штрихов не произвольная, а установлена правилами правописания. В примере В) на рисунке счет доходит то пяти и человек пишет два первых штриха следующего иероглифа, заканчивая счет на семи. Кроме простого счета и учета, унарную систему также используют в компьютерных технологиях и электронике.

Позиционная система счисления

В позиционной системе счисления значение каждого знака, обозначающего цифру, зависит от его положения в числе. Это значение также зависит от основания системы счисления. Позиция обычно называется разрядом. Например, число 101 в двоичной системе не равно ста одному в десятичной. Рассмотрим позиционную систему на примере десятичной:

Первый разряд предназначен для единиц, то есть чисел от нуля до девяти. Цифра первого разряда умножается на десять в нулевой степени (то есть на единицу).
Второй разряд предназначен для десятков и цифру во втором разряде умножают на десять в первой степени.
Третий разряд предназначен для сотен и цифру в третьем разряде умножают на десять во второй степени, и так далее, пока не закончатся разряды.

Чтобы получить значение числа, складывают все числа, полученные выше, то есть значения чисел в каждом разряде. Такой способ написания чисел позволяет работать с большими числами, и не занимает так много места в тексте, по сравнению с непозиционными системами счисления.

Пример использования позиционирования в десятичной системе: 3102 = 3 × 10³ + 1 × 10² + 0 × 10¹ + 2 × 10⁰

Двоичная система

Двоичная система очень широко используется в математике и вычислительной технике. Все возможные числа представлены в ней с помощью только двух цифр, «0» и «1», хотя в некоторых случаях используют и другие знаки, например «+», «–». При переводе чисел из десятичной системы в двоичную получаем: 0=0, 1=1, а для дальнейшего перевода используют правила сложения. Сложение в двоичной системе основано на том же принципе, что и в десятичной. Чтобы добавить к числу единицу пользуются следующим правилом:

Для чисел оканчивающихся нулем, ноль заменяют единицей. Например: 100 (4) + 1 (1) = 101 (5). Здесь и далее для сравнения приведены десятичные числа в скобках.
В числе, оканчивающемся единицей, но не состоящем только из единиц, заменяют первый ноль справа на единицу, а все единицы, за ним следующие (справа от него) заменяют нулями. Например: 1011 (11) + 1 (1) = 1100.
В числе, состоящем из одних единиц, заменяют нулями все единицы, и в начале (слева) добавляют единицу. Например: 111 (7) + 1 (1) = 1000 (8).

При сложении пишут оба числа одно под другим, как при десятичном сложении. Правила при этом следующие: 0+0=0, 1+0=1, а 1+1=10, при этом в правом разряде пишут 0 и переносят 1 в следующий разряд. Например:

То есть, справа налево получаем:

1+1=0, один переносим в следующий разряд
1+1+1=1, один переносим в следующий разряд
1+1=0, один переносим в следующий разряд
1+1+1=1, один переносим в следующий разряд
1+1=10

То есть, получаем 101010.

Вычитание похоже на сложение, только вместо переноса, наоборот, «занимают» единицу из высших разрядов. Умножение тоже похоже на десятичное. Результат перемножения двух единиц — единица, а умножение на ноль дает ноль. Например:

Деление и взятие квадратного корня также мало отличается от работы с десятичными числами.

Классы чисел

Числа объединяются в классы, и некоторые числа могут одновременно входить в несколько классов.

Отрицательные числа

Отрицательные числа обозначают отрицательную величину. Перед ними ставят знак минус, чтобы отличить их от положительных. Например, если человек А должен человеку Б пять рублей, значит у него есть −5 рублей. Здесь –5 — отрицательное число.

Рациональные числа

Рациональные числа — это те числа, которые можно представить в виде дроби, где знаменатель — это положительное натуральное число, а числитель — целое число. Например, 3/4 и −10/5 (то есть, −2) — рациональные числа.

Натуральные числа

Натуральные числа это ноль и положительные целые числа. Например, 7 и 86 766 575 675 456 — натуральные числа.

Целые числа

Целые числа — это ноль, отрицательные и положительные числа, не являющиеся дробями. Например, −65 и 11 223 — целые числа.

Комплексные числа

Комплексные числа получают при сложении действительного (не комплексного) числа и другого действительного числа, умноженного на квадратный корень минус одного. Здесь квадратный корень минус одного называется мнимым числом.

Простые числа

Простые числа — это натуральные числа больше единицы, которые делятся без остатка только на единицу и сами себя. Примеры простых чисел это: 3, 5 и 11. 2 57 885 161 −1 — самое большое известное простое число на февраль 2013 г. В нем содержится 17 425 170 цифр. Простые числа используют в криптосистемах с отрытым ключом. Это вид кодирования применяется в шифровании электронной информации в тех случаях, когда необходимо обеспечить информационную безопасность, например, на сайтах интернет-магазинов, электронных кошельков и банков.

Интересные факты о числах

Особая система записи чисел, чтобы предотвратить мошенничество

В Китае используют отдельную форму записи чисел для бизнеса и финансовых операций. Обычные иероглифы, используемые для названий чисел, слишком просты, и их легко подделать или переделать, добавив к ним всего несколько штрихов. Поэтому на банковских чеках и других финансовых документах обычно используют особые более сложные иероглифы.

Современный счет в торговле

В языках стран, где принята десятичная система счисления, до сих пор сохранились слова, свидетельствующие о том, что ранее там использовалась система с другой основой. Например, в английском языке до сих пор используют слово «дюжина», обозначающее двенадцать. Во многих англоязычных странах в дюжинах считают и продают яйца, мучные изделия, вино и цветы. А в кхмерском языке есть слова для счета фруктов, основанные на двадцатеричной системе.

Произношение названий чисел

Арабская система счисления применяется в Китае и Японии, но в отличие от английского, русского, и многих других языков, числа в китайском и японском языках сгруппированы по десять тысяч. То есть, когда в английском или в русском говорят: сто, потом идут кратные сотни, потом тысяча, кратные тысячи, миллион, и так далее, то в японском и китайском языках идут: сто, кратные ста до 9 999, десять тысяч, кратные десяти тысяч до 999 999, 1 000 000, и так далее.

Несчастливые числа

На Западе, а также во многих странах, где исповедуют христианство, 13 считается несчастливым числом. Историки считают, что это связано с христианством и иудаизмом. Согласно Библии, на Тайной Вечере присутствовало именно тринадцать учеников Иисуса, и тринадцатый, Иуда, после предал Христа. У викингов также существовало поверье о том, что когда тринадцать человек собираются вместе, один из них обязательно умрет в следующем году.

В странах, где говорят по-русски, неудачными считаются четные числа. Вероятно, это связано с верованиями древних славян, которые думали, что четные числа — статичны, неподвижны, закончены в одно целое, а значит — мертвые. Нечетные же, наоборот, подвижны, ищут дополнения, изменяются, а значит — живые. Поэтому четное количество цветов приносят только на похороны, но не дарят живым людям.

В Китае, Корее и Японии не любят число 4, потому, что оно созвучно со словом «смерть». Часто избегают не только саму цифру четыре, но и числа, ее содержащие. Например, часто пропускают такие числа в нумерации этажей и квартир. В Китае также не любят число 7, из-за того, что седьмой месяц в китайском календаре — месяц духов. Считается, что в этот месяц граница между мирами людей и духов исчезает, и духи приходят навещать людей. Число 9 считается неудачным в Японии, так как оно созвучно со словом «страдание».

Несчастливое число в Италии — 17, потому что его написание римскими цифрами — «XVII», что можно переписать как «VIXI», изменив порядок букв. Часто эта фраза была написана на могилах древних римлян и означала «я жил», поэтому ассоциируется с концом жизни и со смертью.

666 — известное многим несчастливое число, также именуемое «числом зверя» в Библии. Некоторые считают, что на самом деле «число зверя» — 616, но упоминание о 666 встречается чаще. Многие верят, что этим числом будет обозначен антихрист, наместник дьявола, и иногда ассоциируют это число с самим дьяволом. Так, некоторые убеждены, что 666 и 616 — это зашифрованное имя римского императора Нерона на древнееврейском и латинском языках соответственно, выраженное цифрами. Вероятность действительно существует, так как Нерон известен гонениями христиан и своим кровавым правлением. Некоторые историки даже считают, что именно Нерон являлся инициатором великого пожара Рима, хотя многие историки не согласны с такой трактовкой событий.

В Афганистане, особенно в Кабуле и его окрестностях, распространился слух о том, что число 39 — позорное число, связанное с проституцией. Согласно этому слуху, в Кабуле живет и работает сутенер, чей номерной знак на машине и номер квартиры содержит это число. Некоторые обвиняют правительство и организованные преступные группировки в том, что те специально распустили такой слух, чтобы покупать в Кабуле машины с такими номерными знаками и перепродавать в отдаленных провинциях, до куда не дошел этот слух. Людей с числом 39 в номерном знаке, номере квартиры или телефона дразнят, и насмехаются над ними, и эта проблема настолько серьезна, что многие изменяют цифры на номерных знаках и всячески стараются скрыть причастность к этому числу. Ходят слухи, что ненависть к числу 39 довела до трагедии. Во время выборов в парламент многие насмехались над кандидатом, чей номер в бюллетене был 39. Во время автомобильной пробки ему начали сигналить и кричать, в результате ситуация на дороге ухудшилась и переросла в аварию, и телохранители, опасающиеся за его жизнь, открыли огонь, в результате убив двоих. Парламентарий и его телохранители отрицают причастность к этому происшествию, никого не привлекли к ответственности, и неизвестно, произошло ли событие в действительности, или это только слухи.

Шестнадцатеричные цифры, преобразование шестнадцатеричного числа в десятичное

27 декабря 2014

Умение преобразовывать шестнадцатеричные числа может быть полезно не только программистам, но и дизайнерам, ведь триада RRGGBB есть не что иное, как «машинные» компоненты для красного, зелёного и синего соответственно — от 0 до 255 каждое. Конечно, графические редакторы содержат палитры со встроенными преобразователями, а стандартный калькулятор операционной системы умеет справляться с этой задачей, но порой гораздо удобнее самому «накинуть +14» к требуемой компоненте, а не запускать сторонние программы.

Прежде, чем я покажу, как (легко) можно переводить числа из шестнадцатеричной системы и более привычную для нас, необходимы дополнительные мероприятия. Все мы в школе учили таблицу умножения, и можем убедиться, что данный навык остался (хотя некоторые им в повседневной жизни не пользуются). Теперь же потребуется немного углубить знания, выучив её вплоть до 16 × 16 .

И последнее: я убеждён, что рядовому пользователю эти навыки не понадобятся с вероятностью 99.…%. В общем, вы предупреждены .

Таблица умножение от 11 до 16

Следующим шагом необходимо соотнести десятичные числа от 10 до 15 с шестнадцатеричными цифрами от A до F.

Таблица соответствия шестнадцатеричных цифр

HEX (шестнадцатеричная)	DEC (десятичная)

1	1
2	2
3	3
4	4
5	5
6	6
7	7
8	8
9	9
A	10
B	11
C	12
D	13
E	14
F	15

А теперь вспомним поразрядное умножение из предыдущей статьи, для цифры 7. Здесь будет лишь поправка на другую систему счисления (не на 10, как там, а на 16).

Обычно в компьютерной литературе, для однозначного указания основания системы счисления, применяется следующая нотация:
— шестнадцатеричное число — 0x100 (256 в десятичной, признак — 0x в начале)
— десятичное число — 100 (наша, человеческая, система счисления)
— восьмеричное число — 0100 (64 в десятичной, признак — ведущий ноль)
— двоичное число — 0b100 (4 в десятичной, признак — 0b в начале)

Преобразование шестнадцатеричного числа в десятичное

Для начала, небольшой рисунок:

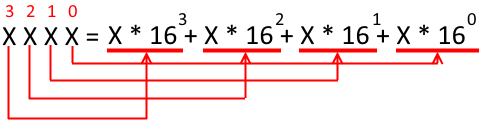
Для преобразования требуется каждую цифру числа умножить на «разряд», в котором оно находится. Из курса начальной школы мы помним, что позиции, занимаемые в числовой строке, называются (справа налево) единицы, десятки, сотни и т. д. Здесь почти то же самое, но с поправкой на систему счисления. Каждый следующий разряд — это +1 степень текущей системы счисления. Любое число в степени ноль — это ноль, в степени 1 — самом число, в степени 2 (квадрат) — число, умноженное само на себя и т. д.

Для наглядности привожу пример. Допустим, возьмём шестнадцатеричное число 0x1F8. Нам требуется перевести его в десятичную систему, поэтому запишем (0x — это признак основания!):

1F8₁₆ = 1₁₆ × 16 2 + F₁₆ × 16 1 + 8₁₆ × 16 0 = 1 × 256 + 15 × 16 + 8 × 1 = 256 + 240 + 8 = 504

Обе таблички нам пригодились: благодаря второй мы переводим числа из шестнадцатеричной системы в десятичную, благодаря первой — легко перемножаем «больше» числа.

Небольшое отступление

А знаете ли вы, что у нас сейчас могла бы использоваться двенадцатеричная система счисления, используемая ещё шумерцами? По одной и версий, этому способствовало количество фаланг пальцев руки. Взгляните на рисунок:

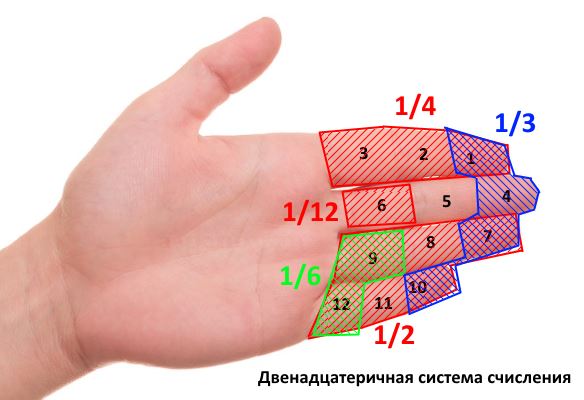
Скорее всего, вам сложно это представить. Но, взглянув на это под другим углом, можем убедиться, что выбор был бы очень хорош, ведь 12 делится без остатка на 2, 3, 4, 6 (в то время, как 10 можно разделить лишь на 2 и 5). Естественно, умножения и деления на степень числа 12 были так же просты, как сейчас аналогичные операции для степени числа 10.

Выучив эти таблицы, любой человек легко сможет переводить компьютерные байты в привычные числа. При желании, как следует потренировавшись и «расширив объём» краткосрочной памяти, станут доступны и более сложные варианты. Но, как уже говорилось чуть ранее, манипуляции с байтами мало кому нужны, не говоря о чём-то большем.