Умножение натуральных чисел: свойства, примеры
Для операции умножения натуральных чисел ℕ характерен ряд результатов, которые справедливы для любых умножаемых натуральных чисел. Эти результаты называются свойствами. В данной статье мы сформулируем свойства умножения натуральных чисел, приведем их буквенные определения и примеры.
Переместительное свойство умножения натуральных чисел
Переместительное свойство часто называют также переместительным законом умножения. По аналогии с переместительным свойством для сложения чисел, оно формулируется так:
Переместительный закон умножения
От перемены мест множителей произведение не меняется.
В буквенном виде переместительное свойство записывается так: a · b = b · a
a и b – любые натуральные числа.
Возьмем любые два натурльных числа и наглядно покажем, что данное свойство справедливо. Вычислим произведение 2 · 6 . По определению произведения, нужно число 2 повторить 6 раз. Получаем: 2 · 6 = 2 + 2 + 2 + 2 + 2 + 2 = 12 . Теперь поменяем множители местами. 6 · 2 = 6 + 6 = 12 . Очевидно, переместительный закон выполняется.
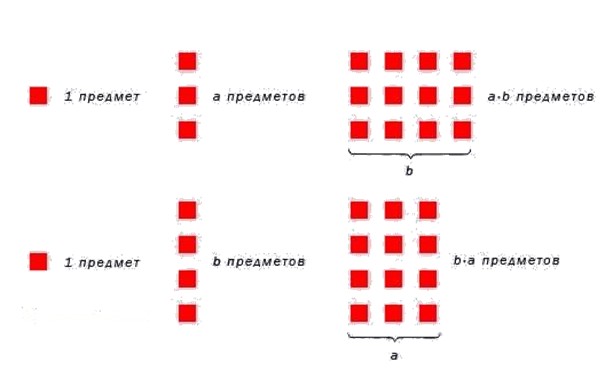
На рисунке ниже проиллюститруем переместительное свойство умножения натуральных чисел.
Сочетательное свойство умножения натуральных чисел
Второе название для сочетательного свойства умножения – ассоциативный закон, или ассоциативное свойство. Вот его формулировка.
Сочетательный закон умножения
Умножение числа a на произведение чисел b и c равносильно умножению произведения чисел a и b на число c .
Приведем формулировку в буквенном виде:
a · b · c = a · b · c
a , b , c – любые натуральные числа. Сочетательный закон работает для трех и более натуральных чисел.
Для наглядности приведем пример. Сначала вычислим значение 4 · 3 · 2 .
4 · 3 · 2 = 4 · 6 = 4 + 4 + 4 + 4 + 4 + 4 = 24
Теперь переставим скобки и вычислим значение 4 · 3 · 2 .
4 · 3 · 2 = 12 · 2 = 12 + 12 = 24
4 · 3 · 2 = 4 · 3 · 2
Как видим, теория совпадает с практикой, и свойство справедливо.
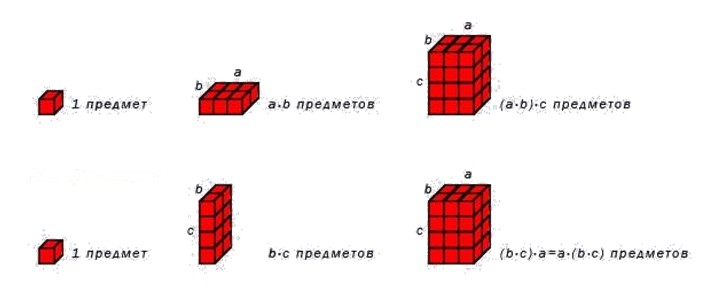
Сочетательное свойство умножения также можно проиллюстрировать с помощью рисунка.
Распределительное свойство относительно умножения
Без распределительного свойста не обойтись, когда в математическом выражении одновременно присутствуют операции умножения и сложения. Это свойство определяет связь между умножением и сложением натуральных чисел.
Распределительное свойство умножения относительно сложения
Умножения суммы чисел b и c на число a равносильно сумме произведений чисел a и b и a и c .
Запишем в форме буквенного выражения:
a · b + c = a · b + a · c
a , b , c – любые натуральные числа.
Теперь на наглядном примере покажем, как работает это свойство. Вычислим значение выражения 4 · 3 + 2 .
4 · 3 + 2 = 4 · 3 + 4 · 2 = 12 + 8 = 20
С другой стороны 4 · 3 + 2 = 4 · 5 = 20 . Справедливость распределительного свойства умножения относительно сложения показана наглядно.
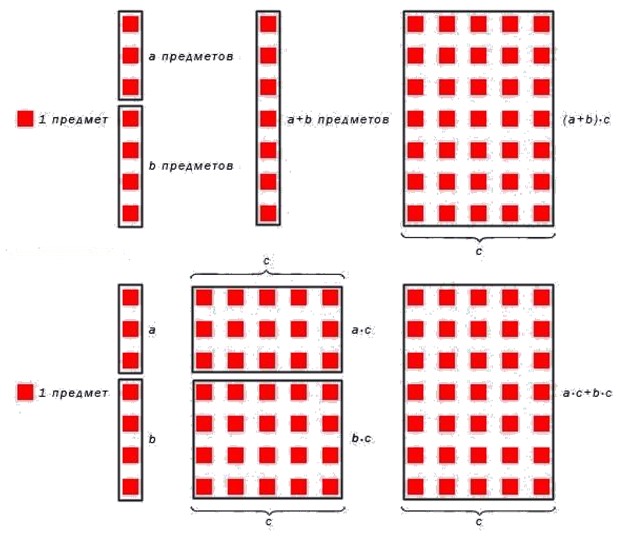
Для лучшего понимания приведем рисунок, иллюстрирующий суть умножения числа на сумму чисел.
Распределительное свойство умножения относительно вычитания
Распределительное свойство умножения относительно вычитания формулируется аналогично данному свойству относительно сложения, следует лишь учитывать знак операции.
Распределительное свойство умножения относительно вычитания
Умножения разности чисел b и c на число a равносильно разности произведений чисел a и b и a и c .
Запишем в форме буквенного выражения:
a · b – c = a · b – a · c
a , b , c – любые натуральные числа.
В предыдущем примере заменим “плюс” на “минус” и запишем:
4 · 3 – 2 = 4 · 3 – 4 · 2 = 12 – 8 = 4
С другой стороны 4 · 3 – 2 = 4 · 1 = 4 . Таким образом, справедливость свойства умножения натуральных чисел относительно вычитания показана наглядно.
Умножение единицы на натуральное число
Умножение единицы на любое натуральное число в результате дает данное число.
По определению операции умножения, произведение чисел 1 и a равно сумме, в котором слагаемое 1 повторяется a раз.
1 · a = ∑ i = 1 a 1
Умножение натурального числа a на единицу представляет собой сумму, состоящую из одого слагаемого a . Таким образом, переместительное свойство умножения остается справедливым:
Умножение нуля на натуральное число
Число 0 не входит в множество натуральных чисел. Тем не менее, есть смысл рассмотреть свойство умножения нуля на натуральное число. Данное свойство часто используется при умножении натуральных чисел столбиком.
Умножение нуля на натуральное число
Произведение числа 0 и любого натурального числа a равно числу 0 .
По определению, произведение 0 · a равно сумме, в которой слагаемое 0 повторяется a раз. По свойствам сложения, такая сумма равна нулю.
В результате умножения единицы на нуль получается нуль. Произведение нуля на сколь угодно большое натуральное число также дает в результате нуль.
Напимер: 0 · 498 = 0 ; 0 · 9638854785885 = 0
Справедливо и обратное. Произведение числа на нуль также дает в результате нуль: a · 0 = 0 .
Свойства умножения и деления

О чем эта статья:
Свойства умножения
Умножение — арифметическое действие, в котором участвуют два аргумента: множимый и множитель. Результат их умножения называется произведением.
Узнаем, какие бывают свойства умножения и как их применять.
Переместительное свойство умножения
От перестановки мест множителей произведение не меняется.
То есть, для любых чисел a и b верно равенство: a * b = b * a.
Это свойство можно применять к произведениям, в которых больше двух множителей.
- 6 * 5 = 5 * 6 = 30;
- 4 * 2 * 3 = 3 * 2 * 4 = 24.
Сочетательное свойство умножения
Произведение трех и более множителей не изменится, если какую-то группу множителей заменить их произведением.
То есть, для любых чисел a, b и c верно равенство: a * b * c = (a * b) * c = a * (b * c).
-
3 * 2 * 5 = 3 * (2 * 5) = 3 * 10 = 30
Сочетательное свойство можно использовать, чтобы упростить вычисления при умножении. Например: 25 * 15 * 4 = (25 * 4) * 15 = 100 * 15 = 1500.
Если не применять сочетательное свойство и вычислять последовательно, решение будет значительно сложнее: 25 * 15 * 4 = (25 * 15) * 4 = 375 * 4 = 1500.
Распределительное свойство умножения относительно сложения
Чтобы умножить сумму на число, нужно умножить на это число каждое слагаемое и сложить полученные результаты.
То есть, для любых чисел a, b и c верно равенство: (a + b) * c = a * c + b * c.
Это свойство работает с любым количеством слагаемых: (a + b + с + d) * k = a * k + b * k + c * k + d * k.
В обратную сторону распределительное свойство умножения относительно сложения звучит так:
Чтобы число умножить на сумму чисел, нужно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
Распределительное свойство умножения относительно вычитания
Чтобы умножить разность на число, нужно умножить на это число сначала уменьшаемое, затем вычитаемое, и из первого произведения вычесть второе.
То есть, для любых чисел a, b и c верно равенство: (a − b) * c = a * c − b * c.
В обратную сторону распределительное свойство умножения относительно вычитания звучит так:
Чтобы число умножить на разность чисел, нужно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.
Свойство нуля при умножении
Если в произведении хотя бы один множитель равен нулю, то само произведение будет равно нулю.
То есть, для любых чисел a, b и c верно равенство:
0 * a * b * c = 0.
Свойство единицы при умножении
Если умножить любое целое число на единицу, то в результате получится это же число.
То есть, умножение на единицу не изменяет умножаемое число: a * 1 = a.
Свойства деления
Деление — арифметическое действие обратное умножению. В результате деления получается число (частное), которое при умножении на делитель дает делимое.
Основные свойства деления целых чисел
И еще одно важное свойство деления, которое проходят в 5 классе:
Если делимое и делитель умножить или разделить на одно и тоже натуральное число, то их частное не изменится.
В буквенной форме это свойство выглядит так: a : b = (a * k) : (b * k), где k — любое натуральное число.
Применим свойства деления на практике.
Пример 1
Мама купила 6 кг конфет и разложила их в три пакета. Сколько килограммов конфет в каждом пакете?
Так как в каждом пакете одинаковое количество конфет, разделим 6 кг на три равные части: 6 : 3 = 2. Значит в каждом пакете по 2 кг конфет.
Пример 2
Вычислить: 500 * (100 : 5).
Как решаем: 500 * (100 : 5) = (500 * 100) : 5 = 50000 : 5 = 10000.
Ответ: 500 * (100 : 5) = 10000.
Пример 3
Упростить выражение: 27a – 16a.
Как решаем: 27a – 16a = a * 27 – a * 16 = a * (27 – 16) = a * 11 = 11a.
Свойства умножения и деления помогают упрощать выражения. То есть, если запомнить эти свойства и научиться их применять, то решать задачки можно быстрее.
Законы математики
В нашей жизни есть законы, которые надо соблюдать. Соблюдение законов гарантирует стабильность и гармоничное развитие. Несоблюдение же законов приводит к печальным последствиям.
У математики есть свои законы, которые тоже следует соблюдать. Несоблюдение законов математики приводит в лучшем случае к тому, что оценка учащегося снижается, а в худшем случае приводит к тому, что падают самолёты, зависают компьютеры, улетают крыши домов от сильного ветра, снижается качество связи и тому подобные нехорошие явления.
Законы математики состоят из простых свойств. Эти свойства нам знакомы со школы. Но не мешает вспомнить их ещё раз, а лучше всего записать или выучить наизусть.
В данном уроке мы рассмотрим лишь малую часть законов математики. Их нам будет достаточно для дальнейшего изучения математики.
Переместительный закон сложения
Переместительный закон сложения говорит о том, что от перестановки мест слагаемых сумма не изменяется. Действительно, прибавьте пятерку к двойке — получите семёрку. И наоборот, прибавьте двойку к пятерке — опять получите семёрку:
Если положить на одну чашу весов 10 килограмм яблок и на другую чашу так же положить 10 килограмм яблок, то весы выровнятся, и не важно, что яблоки в пакетах лежат вразброс. Если мы возьмём пакет с весов и перемешаем яблоки находящиеся в нём, словно шары в лотерейном мешке, пакет всё так же будет весить 10 килограмм. От перестановки мест слагаемых сумма не изменится. Слагаемые в данном случае это яблоки, а сумма это итоговый вес.
Таким образом, между выражениями 5 + 2 и 2 + 5 можно поставить знак равенства. Это будет означать, что их сумма равна:
Полагаем что, вы изучили один из предыдущих уроков, который назывался выражения, поэтому мы без тени смущения запишем переместительный закон сложения с помощью переменных:
Записанный переместительный закон сложения будет работать для любых чисел. Например, возьмём любых два числа. Пусть а = 2, b = 3 . Мы присвоили переменным a и b значения 2 и 3 соответственно. Эти значения отправятся в главное выражение a + b = b + a и подставятся куда нужно. Число 2 подставится вместо а , число 3 место b
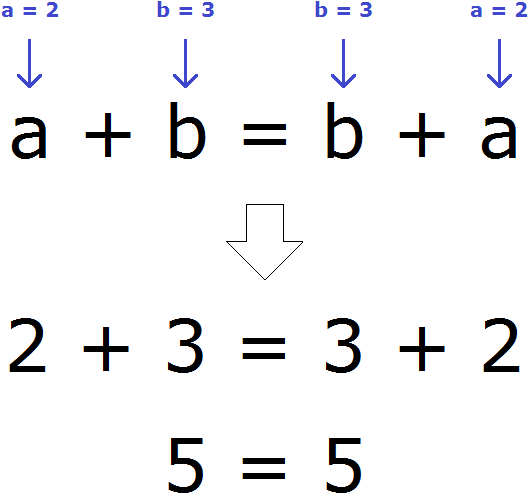
Сочетательный закон сложения
Сочетательный закон сложения говорит о том, что результат сложения нескольких слагаемых не зависит от порядка действий. Этот закон позволяет группировать слагаемые для удобства их вычислений.
Рассмотрим сумму из трёх слагаемых:
Чтобы вычислить данное выражение, можно сначала сложить числа 2 и 3 и полученный результат сложить с числом 5. Для удобства сумму чисел 2 и 3 можно заключить в скобки, указывая тем самым, что эта сумма будет вычислена в первую очередь:
2 + 3 + 5 = (2 + 3) + 5 = 5 + 5 = 10
Либо можно сложить числа 3 и 5, затем полученный результат сложить с числом 2
2 + 3 + 5 = 2 + (3 + 5) = 2 + 8 = 10
Видно, что в обоих случаях получается один и тот же результат.
Таким образом, между выражениями (2 + 3) + 5 и 2 + (3 + 5) можно поставить знак равенства, поскольку они равны одному и тому же значению:
(2 + 3) + 5 = 2 + (3 + 5)
Запишем сочетательный закон сложения с помощью переменных:
(a + b) + c = a + (b + c)
Переместительный закон умножения
Переместительный закон умножения говорит о том, что если множимое и множитель поменять местами, то произведение не изменится. Давайте проверим так ли это. Умножим пятерку на двойку, а затем наоборот двойку на пятерку.
В обоих случаях получается один и тот же результат, поэтому между выражениями 5 × 2 и 2 × 5 можно поставить знак равенства, поскольку они равны одному и тому же значению:
5 × 2 = 2 × 5
Запишем переместительный закон умножения с помощью переменных:
Для записи законов в качестве переменных необязательно использовать именно буквы a и b . Можно использовать любые другие буквы, например c и d или x и y . Тот же переместительный закон умножения можно записать следующим образом:
Сочетательный закон умножения
Сочетательный закон умножения говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.
Рассмотрим следующее выражение:
Данное выражение можно вычислять в любом порядке. Сначала можно перемножить числа 2 и 3, и полученный результат умножить на 4:
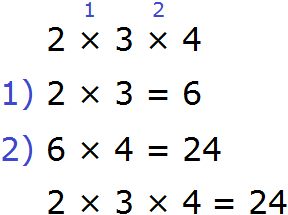
Либо сначала можно перемножить числа 3 и 4, и полученный результат перемножить с числом 2
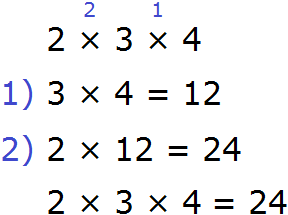
Таким образом, между выражениями (2 × 3) × 4 и 2 × (3 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:
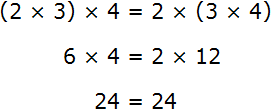
Запишем сочетательный закон умножения с помощью переменных:
a × b × с = (a × b) × с = a × (b × с)
Пример 2. Найти значение выражения 1 × 2 × 3 × 4
Данное выражение можно вычислять в любом порядке. Вычислим его слева направо в порядке следования действий:
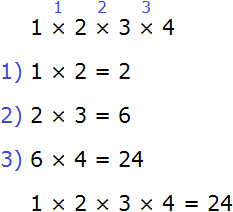
Распределительный закон умножения
Распределительный закон умножения позволяет умножить сумму на число или число на сумму.
Рассмотрим следующее выражение:
Мы знаем, что сначала надо выполнить действие в скобках. Выполняем:
В главном выражении (3 + 5) × 2 выражение в скобках заменим на полученную восьмёрку:
8 × 2 = 16
Получили ответ 16. Этот же пример можно решить с помощью распределительного закона умножения. Для этого каждое слагаемое, которое в скобках, нужно умножить на 2, затем сложить полученные результаты:
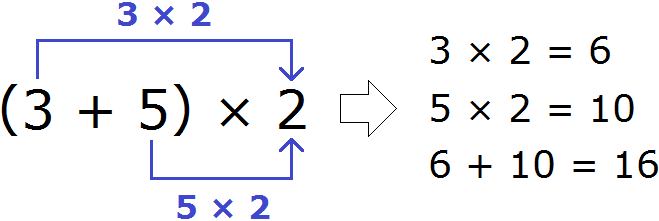
Мы рассмотрели распределительный закон умножения слишком развёрнуто и подробно. В школе этот пример записали бы очень коротко. К такой записи тоже надо привыкать. Выглядит она следующим образом:
(3 + 5) × 2 = 3 × 2 + 5 × 2 = 6 + 10 = 16
(3 + 5) × 2 = 6 + 10 = 16
Теперь запишем распределительный закон умножения с помощью переменных:
(a + b) × c = a × c + b × c
Давайте внимательно посмотрим на начало этого распределительного закона умножения. Начало у него выглядит так: (a + b) × c.
Если рассматривать выражение в скобках (a + b), как единое целое, то это будет множимое, а переменная с будет множителем, поскольку соединены они знаком умножения ×
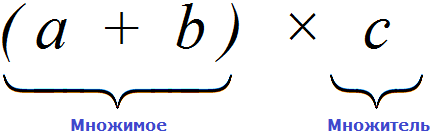
Из переместительного закона умножения мы узнали, что если множимое и множитель поменять местами, то произведение не изменится.
Если множимое (a + b) и множитель c поменять местами, то получим выражение c × (a + b) . Тогда получится, что мы умножаем переменную c на сумму (a + b) . Для выполнения такого умножения, опять же применяется распределительный закон умножения. В данном случае переменную c нужно умножить на каждое слагаемое в скобках:
c × (a + b) = c × a + c × b
Пример 2. Найти значение выражения 5 × (3 + 2)
Умножим число 5 на каждое слагаемое в скобках и полученные результаты сложим:
5 × (3 + 2) = 5 × 3 + 5 × 2 = 15 + 10 = 25
Пример 3. Найти значение выражения 6 × (5 + 2)
Умножим число 6 на каждое слагаемое в скобках и полученные результаты сложим:
6 × (5 + 2) = 6 × 5 + 6 × 2 = 30 + 12 = 42
Если в скобках располагается не сумма, а разность, то сначала нужно умножить множимое на каждое число, которое в скобках. Затем из полученного первого числа вычесть второе число. В принципе, ничего нового.
Пример 4. Найти значение выражения 5 × (6 − 2)
Умножим 5 на каждое число в скобках. Затем из полученного первого числа вычтем второе число:
5 × (6 − 2) = 5 × 6 − 5 × 2 = 30 − 10 = 20
Пример 5. Найти значение выражения 7 × (3 − 2)
Умножим 7 на каждое число в скобках. Затем из полученного первого числа вычтем второе число:
Распределительное свойство умножения


Средняя оценка: 4.2
Всего получено оценок: 133.
Средняя оценка: 4.2
Всего получено оценок: 133.
Свойства умножения – это, прежде всего, возможность быстро произвести вычисление. Знание распределительного свойства поможет вам без проблем посчитать сложный пример или решить уравнение. Рассмотрим в в подробностях применение распределительного свойства умножения.
Умножение
Умножение – это сокращенный процесс сложения. Что это значит? Первый множитель это число, которое складывается само с собой число раз, равное второму множителю.
3*6=3+3+3+3+3+3=18 – вот как это выглядит на практике. Умножение было изобретено во время, когда потребовались большие вычисления, которые неудобно записывать в виде сложения.
Можно 3 раза сложить число 6, а можно 6 раз сложить число 3. Результат от этого не поменяется, в этом заключается смысл переместительного свойства умножения.
Умножение позволило решить достаточно много проблем, но вместе с ним в математику пришло и деление, как противоположная операция.
Свойства умножения
Всего у умножения 3 свойства:
- Переместительное: от перемены мест множителя произведение не меняется. Для произведения в 2 множителя это не критично, но для примеров с 3 и более множителями, это свойство может сэкономить время.
- Сочетательное свойство. Это свойство так же используется для примеров от 3 и более множителей. Суть свойства в том, что можно перемножить первые два множителя, а потом результат умножить на третий. Причем порядок перемножения может быть любым.
- Распределительное свойство. Это свойство применяется для умножения числа на сумму или разность. Это свойство сокращает время решения при правильном подходе. Суть свойства в том, что при умножении числа на сумму или разность, то можно каждое слагаемое умножить на число, а потом выполнить сложение.
Распределительное свойство
Распределительно свойство можно использовать для быстрого расчета. Рассмотрим большой пример для 6 класса с применением этого свойства умножения:
Обратите внимание, что пример представляет собой сумму слагаемых, каждый из которых представлен произведением. Рассмотрим каждое произведение в отдельности, а потом сложим результаты.
- $$(<3over<4>>-<2over<8>>)*(18-16)$$ – Найдем значение дроби в первой скобке, а затем умножим его на уменьшаемое и делитель во второй скобке по распределительному свойству.
$$<1over<2>>*18-<1over<2>>*16=9-8=1$$ – такие ответы иногда бывают в сложных на вид примерах.
- $$<1over<15>>*((13+30)-(16-3))$$ – здесь слишком много слагаемых, чтобы использовать распределительное свойство, поэтому просто выполним действия во второй скобке и произведем умножение:
- $$<16over<17>>*(-34+17)$$ – обратите внимание, в знаменателе дроби стоит число 17, которое является делителем для чисел в скобках. Это признак того, что можно и нужно воспользоваться распределительным свойством умножения.
- $$(<20over<21>>-<38over<42>>)*(<7over<3>>+<56over<3>>)$$ – если посмотреть на вторую скобку, то видно, что в ней можно выполнить сложение дробей без приведения к общему знаменателю.
$$(<7over<3>>+<56over<3>>)=<63over<3>>=21$$ – теперь воспользуемся распределительным свойством и умножим число 21 на каждое из чисел в скобках:
- Сведем все получившиеся значения в один пример и вычислим результат:
1+2+16-1=18 – вот такой маленький ответ получился в большом примере.
При решении этого примера, важно понять, что не всегда нужно использовать распределительное свойство умножения. Важно понимать, когда лучше им воспользоваться, а когда решить другим путем.

Что мы узнали?
Мы узнали, что такое умножение. Поговорили о свойствах умножения и особенно выделили распределительное свойство умножения. Решили большой пример на тему применения этого свойства.
Распределительное свойство сложения и умножения: формулы и примеры
Благодаря знанию распределительного свойства умножения и сложения, можно устно решить сложные, на первый взгляд, примеры. Изучается данное правило на уроках алгебры в 7 классе. Задания с использованием данного правила встречаются на ОГЭ и ЕГЭ по математике.
Распределительное свойство умножения
Для того, чтобы произвести умножение суммы некоторых чисел, можно умножить каждое слагаемое по отдельности и сложить полученные результаты.
Проще говоря, a × (в + с) = ав + ас или (в + с) ×а = ав + ас.
 Вам будет интересно: О том, как становился современный кыргызский язык
Вам будет интересно: О том, как становился современный кыргызский язык

Также, для упрощения решения, данное правило действует и в обратном порядке: а×в + а×с = а × (в + с), то есть общий множитель выносится за скобки.
Используя распределительное свойство сложения, можно решить следующие примеры.
 × 7. Выполните вычисления: 20 × 7 + 8 × 7 = 140 + 56 = 196. Ответ: 196.
× 7. Выполните вычисления: 20 × 7 + 8 × 7 = 140 + 56 = 196. Ответ: 196.Это же правило действует не только на сумму, но и на разность двух и более выражений.
Распределительное свойство умножения относительно разности
Для того, чтобы выполнить умножение разности на число, следует умножить на него уменьшаемое, а затем вычитаемое и выполнить вычисление полученных результатов.
a × (в – с) = а×в – а×с или (в – с) × а = а×в – а×с.
Пример 1: 14 × (10 – 2). Используя распределительный закон, умножьте 14 на оба числа: 14× 10 -14 × 2. Найдите разность полученных значений: 140 – 28 = 112 и запишите полученный результат. Ответ: 112.

Пример 2: 8 × (1 + 20). Аналогично решается данное задание: 8 × 1 + 8 × 20 = 8 + 160 = 168. Ответ: 168.
Пример 3: 27× 3. Найдите значение выражения, пользуясь изученным свойством. Представьте 27 как разность двух чисел 30 и 3, вот так: 27 × 3 = (30 – 3) × 3 = 30 × 3- 3 × 3 = 90 – 9 = 81. Ответ: 81.
Применение свойства для более двух слагаемых
Распределительное свойство умножения применяется не только для двух слагаемых, а для абсолютно любого количества, в таком случае формула имеет данный вид:
а × (в + с+ d) = a×в +a×с+ a×d.
а × (в – с – d) = a×в – a×с – a×d.
Пример 1: 354×3. Представьте 354 как сумму трех чисел: 300, 50 и 3: (300 + 50 + 3) ×3= 300×3 + 50×3 + 3×3 = 900 + 150 + 9 =1059. Ответ: 1059.
Упростите несколько выражений, используя упомянутое ранее свойство.

Пример 2: 5 × (3х + 14у). Раскройте скобки, используя распределительный закон умножения: 5 × 3х + 5 × 14у = 15х + 70у. 15 х и 70у сложить нельзя, так как слагаемые не являются подобными и имеют различную буквенную часть. Ответ: 15х + 70у.
Пример 3: 12 × (4с – 5d). Учитывая правило, умножьте на 12 и 4с и 5d: 12 × 4с – 12 × 5d = 48с – 60d. Ответ: 48с – 60d.
Используя при решении примеров распределительное свойство сложения и умножения:
- с легкостью решаются сложные примеры, их решение можно свести к устному счету;
- заметно экономится время при решении сложных, на первый взгляд, задач;
- благодаря полученным знаниям, можно с легкостью упростить выражения.
Сочетательное и распределительное свойства умножения
Начертим на листке в клетку прямоугольник со сторонами 5 см и 3 см. Разобьем его на квадраты со стороной 1 см (рис. 143 ). Подсчитаем количество клеток, расположенных в прямоугольнике. Это можно сделать, например, так.
Количество квадратов со стороной 1 см равно 5 * 3 . Каждый такой квадрат состоит из четырех клеток. Поэтому общее число клеток равно ( 5 * 3 ) * 4 .
Эту же задачу можно решить иначе. Каждый из пять столбцов прямоугольника состоит из трех квадратов со стороной 1 см. Поэтому в одном столбце содержится 3 * 4 клеток. Следовательно, всего клеток будет 5 * ( 3 * 4 ).
Подсчет клеток на рисунке 143 двумя способами иллюстрирует сочетательное свойство умножения для чисел 5, 3 и 4 . Имеем: ( 5 * 3 ) * 4 = 5 * ( 3 * 4 ).
Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел.
В буквенном виде это свойство записывают так:
(ab)c = a(bc)
Из переместительного и сочетательно свойств умножения следует, что при умножении нескольких чисел множители можно менять местами и заключать в скобки, тем самым определяя порядок вычислений.
Например, верны равенства:
17 * 2 * 3 * 5 = ( 17 * 3 ) * ( 2 * 5 ).
На рисунке 144 отрезок AB делит рассмотренный выше прямоугольник на прямоугольник и квадрат.
Подсчитаем количество квадратов со стороной 1 см двумя способами.
С одной стороны, в образовавшемся квадрате их содержится 3 * 3, а в прямоугольнике − 3 * 2 . Всего получим 3 * 3 + 3 * 2 квадратов. С другой стороны, в каждой из трех строчек данного прямоугольника находится 3 + 2 квадрата. Тогда их общее количество равно 3 * ( 3 + 2 ).
Равенсто 3 * ( 3 + 2 ) = 3 * 3 + 3 * 2 иллюстрирует распределительное свойство умножения относительно сложения.
Чтобы число умножить на сумму двух чисел, можно это число умножить на каждое слагаемое и полученные произведения сложить.
В буквенном виде это свойство записывают так:
a(b + c) = ab + ac
Из распределительного свойства умножения относительно сложения следует, что
Это равенство позволяет формулу P = 2 a + 2 b для нахождения периметра прямоугольника записать в таком виде:
Заметим, что распределительное свойство справедливо для трех и более слагаемых. Например:
a(m + n + p + q) = am + an + ap + aq.
Также справедливо распределительное свойство умножения относительно вычитания: если b > c или b = c, то
a(b − c) = ab − ac
Пример 1 . Вычислите удобным способом:
2 ) 329 * 75 + 329 * 246 .
1 ) Используем переместительное, а затме сочетательное свойства умножения:
25 * 867 * 4 = 867 * ( 25 * 4 ) = 867 * 100 = 86 700 .
329 * 754 + 329 * 246 = 329 * ( 754 + 246 ) = 329 * 1 000 = 329 000 .
Пример 2 . Упростите выражение:
1 ) Используя переместительное и сочетательное свойства умножения, получаем:
4 a * 3 b = ( 4 * 3 ) * ab = 12 ab.
2 ) Используя распределительное свойство умножения относительно вычитания, получаем:
18 m − 13 m = m( 18 − 13 ) = m * 5 = 5 m.
Пример 3 . Запишите выражение 5 ( 2 m + 7 ) так, чтобы оно не содержало скобок.
Согласно распределительному свойству умножения относительно сложения имеем:
5 ( 2 m + 7 ) = 5 * 2 m + 5 * 7 = 10 m + 35 .
Такое преобразование называют раскрытием скобок.
Пример 4 . Вычислите удобным способом значение выражения 125 * 24 * 283 .
125 * 24 * 283 = 125 * 8 * 3 * 283 = ( 125 * 8 ) * ( 3 * 283 ) = 1 000 * 849 = 849 000 .
Пример 5 . Выполните умножение: 3 сут 18 ч * 6 .
3 сут 18 ч * 6 = 18 сут 108 ч = 22 сут 12 ч.
При решении примера было использовано распределительное свойство умножения относительно сложения:
3 сут 18 ч * 6 = ( 3 сут + 18 ч) * 6 = 3 сут * 6 + 18 ч * 6 = 18 сут + 108 ч = 18 сут + 96 ч + 12 ч = 18 сут + 4 сут + 12 ч = 22 сут 12 ч.
Свойства умножения натуральных чисел.
Отталкиваясь от общего представления об умножении натуральных чисел, можно отметить ряд результатов, характерных для этого действия. Эти неотъемлемые результаты называются свойствами умножения натуральных чисел. В этой статье мы подробно на примерах рассмотрим основные свойства умножения натуральных чисел и запишем их при помощи букв.
Навигация по странице.
- Переместительное свойство умножения натуральных чисел.
- Сочетательное свойство умножения натуральных чисел.
- Распределительное свойство умножения относительно сложения.
- Распределительное свойство умножения относительно вычитания.
- Свойство умножения единицы на натуральное число.
- Свойство умножения нуля на натуральное число.
Переместительное свойство умножения натуральных чисел.
Умножение двух натуральных чисел обладает переместительным свойством. Приведем формулировку этого свойства: произведение двух натуральных чисел не изменяется при перестановке множителей местами. С помощью букв переместительное свойство умножения можно записать так: a·b=b·a , где a и b могут быть любыми натуральными числами (при необходимости смотрите статью буквенные выражения).
Рассмотрим пример, подтверждающий справедливость переместительного свойства умножения двух натуральных чисел. Отталкиваясь от смысла умножения двух натуральных чисел, вычислим произведение чисел 2 и 6 , а также произведение чисел 6 и 2 , и проверим равенство результатов умножения. Произведение чисел 6 и 2 равно сумме 6+6 , из таблицы сложения находим 6+6=12 . А произведение чисел 2 и 6 равно сумме 2+2+2+2+2+2 , которая равна 12 (при необходимости смотрите материал статьи сложение трех и большего количества чисел). Следовательно, 6·2=2·6 .
Приведем рисунок, иллюстрирующий переместительное свойство умножения двух натуральных чисел.

Сочетательное свойство умножения натуральных чисел.
Озвучим сочетательное свойство умножения натуральных чисел: умножить данное число на данное произведение двух чисел – это то же самое, что умножить данное число на первый множитель, и полученный результат умножить на второй множитель. То есть, a·(b·c)=(a·b)·c , где a , b и c могут быть любыми натуральными числами (в круглые скобки заключены выражения, значения которых вычисляются в первую очередь).
Приведем пример для подтверждения сочетательного свойства умножения натуральных чисел. Вычислим произведение 4·(3·2) . По смыслу умножения имеем 3·2=3+3=6 , тогда 4·(3·2)=4·6=4+4+4+4+4+4=24 . А теперь выполним умножение (4·3)·2 . Так как 4·3=4+4+4=12 , то (4·3)·2=12·2=12+12=24 . Таким образом, справедливо равенство 4·(3·2)=(4·3)·2 , подтверждающее справедливость рассматриваемого свойства.
Покажем рисунок, иллюстрирующий сочетательное свойство умножения натуральных чисел.

В заключении этого пункта отметим, что сочетательное свойство умножения позволяет однозначно определить умножение трех и большего количества натуральных чисел.
Распределительное свойство умножения относительно сложения.
Следующее свойство связывает сложение и умножение. Оно формулируется так: умножить данную сумму двух чисел на данное число – это то же самое, что сложить произведение первого слагаемого и данного числа с произведением второго слагаемого и данного числа. Это так называемое распределительное свойство умножения относительно сложения.
С помощью букв распределительное свойство умножения относительно сложения записывается как (a+b)·c=a·c+b·c (в выражении a·c+b·c сначала выполняется умножение, после чего – сложение, подробнее об этом написано в статье порядок выполнения действий), где a , b и c – произвольные натуральные числа. Отметим, что силу переместительного свойства умножения, распределительное свойство умножения можно записать в следующем виде: a·(b+c)=a·b+a·c .
Приведем пример, подтверждающий распределительное свойство умножения натуральных чисел. Проверим справедливость равенства (3+4)·2=3·2+4·2 . Имеем (3+4)·2=7·2=7+7=14 , а 3·2+4·2=(3+3)+(4+4)=6+8=14 , следовательно, равенство (3+4)·2=3·2+4·2 верно.
Покажем рисунок, соответствующий распределительному свойству умножения относительно сложения.

Распределительное свойство умножения относительно вычитания.
Умножение и вычитание натуральных чисел связываются распределительным свойством. Озвучим его формулировку: умножить данную разность двух натуральных чисел на данное натуральное число – это все равно, что из произведения уменьшаемого и данного числа вычесть произведение вычитаемого и данного числа.
С помощью букв распределительное свойство умножения относительно вычитания можно записать как (a−b)·c=a·c−b·c , где a , b и c – некоторые натуральные числа. В силу переместительного свойства умножения также справедлива формула вида a·(b−c)=a·b−a·c .
Проверим справедливость распределительного свойства умножения относительно вычитания на примере. Убедимся, что верно равенство 3·(4−2)=3·4−3·2 . Так как 4−2=2 (при необходимости смотрите раздел теории вычитание с использованием таблицы сложения), то произведение 3·(4−2) равно произведению 3·2 , а 3·2=3+3=6 . Теперь вычислим разность 3·4−3·2 . Имеем 3·4−3·2=(3+3+3+3)−(3+3)=12−6=6 . Таким образом, равенство 3·(4−2)=3·4−3·2 верное.
Свойство умножения единицы на натуральное число.
Следующее свойство связано с умножением единицы и натурального числа. По смыслу умножения, произведение единицы и данного натурального числа n равно сумме n слагаемых, каждое из которых равно единице. Следовательно,  .
.
Например, произведение чисел 1 и 37 равно 37 ; результат умножения 1 и 1 004 есть число 1 004 .
В свою очередь, произведение n·1 лишено смысла (по смыслу умножения это произведение представляет собой сумму одного слагаемого, равного числу n , но сложение мы определяли для двух и более слагаемых). Чтобы оставалось справедливым переместительное свойство умножения, будем считать верным равенство n·1=n .
К примеру, произведение 298 и 1 равно 298 , а если умножить 71 на 1 , то получим 71 .
Итак, произведение двух натуральных чисел, одно из которых равно единице, равно другому числу. Последнее утверждения является формулировкой свойства умножения единицы и натурального числа. С помощью букв это свойство умножения записывается так: 1·n=n·1=n , где n – любое натуральное число.
Свойство умножения нуля на натуральное число.
Хотя нуль не является натуральным числом, но все же свойство умножения нуля и натурального числа мы рассмотрим в этой статье. Это связано с тем, что данное свойство используется при умножении натуральных чисел столбиком.
Если придерживаться смысла умножения, то произведение 0·n , где n – произвольное натуральное число, большее единицы, представляет собой сумму n слагаемых, каждое из которых равно нулю. Таким образом,  . Свойства сложения позволяют нам утверждать, что последняя сумма равна нулю.
. Свойства сложения позволяют нам утверждать, что последняя сумма равна нулю.
Чтобы сохранить справедливость свойства умножения натурального числа на единицу, которое мы разбирали в предыдущем пункте, будем считать верным следующее равенство 0·1=0 .
Таким образом, для любого натурального числа n выполняется равенство 0·n=0 .
Чтобы оставалось справедливым переместительное свойство умножения примем также справедливость равенства n·0=0 для любого натурального числа n .
Итак, произведение нуля и натурального числа равно нулю, то есть 0·n=0 и n·0=0 , где n – произвольное натуральное число. Последнее утверждение представляет собой формулировку свойства умножения натурального числа и нуля.
В заключении приведем пару примеров, связанных с разобранным в этом пункте свойством умножения. Произведение чисел 45 и 0 равно нулю. Если умножить 0 на 45 970 , то тоже получим нуль.
Теперь можно смело начинать изучение правил, по которым проводится умножение натуральных чисел.