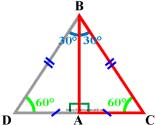
Площадь треугольника через радиус описанной окружности доказательство

В школьном курсе геометрии доказано несколько формул площади треугольника. Напомним их.

Пусть `A`, `B` и `C` – углы треугольника`ABC`; `a`, `b` и `c` – противолежащие этим углам стороны; `h_a`, `h_b` и `h_c` – высоты к этим сторонам; `r` – радиус вписанной окружности;`R` – радиус описанной окружности; `2p=(a+b+c)` – периметр треугольника; `S` – площадь треугольника

`S=1/2ah_a=1/2bh_b=1/2ch_c`,	(1)
`S=1/2 ab sinC=1/2acsinB=1/2bcsinA`,	(2)
`S=pr`,	(3)
``S=sqrt(p(p-a)(p-b)(p-c))` – формула Герона,	(4)
`S=(abc)/(4R)`.	(5)

При вычислении площади из этих формул следует выбрать ту, которая в условиях конкретной задачи приводит к более простому решению.

Для примера, рассмотрим два треугольника:

`DeltaABC:` `AB=13`, `BC=14`, `AC=15`;

`DeltaKML:` `KL=sqrt(13)`, `LM=sqrt(14)`, `KM=sqrt(15)`;

Надо найти площадь и радиус описанной окружности.

Для треугольника `ABC` удобен ход решения такой:

`p=1/2(AB+BC+AC)=21`, по формуле Герона

`S_(ABC)=sqrt(21*6*7*8)= ul(84)` и по формуле (5)

Для треугольника `KLM` вычисленная по формуле Герона затруднительны, более простой путь – найти косинус, например, угла `M`. По теореме косинусов

тогда `sinM=sqrt(1-64/(210))=(sqrt(146))/(sqrt(14)*sqrt(15))` и по формуле (2):

тогда `R=(KL)/(2sinM)=ul((sqrt(13)*sqrt(14)*sqrt(15))/(2*sqrt(146)))=(sqrt(13)*sqrt7*sqrt(15))/(2*sqrt(73))` (точно также по формуле 5).

Сравнение площадей треугольников обычно опирается на одно из следующих утверждений:

$$ 2.<1>^<○>$$. Площади треугольников с одинаковой высотой относятся как длины соответствующих оснований. В частности, если точка `D` лежит на основании `AC` (рис. 6а), то

$$ 2.<2>^<○>$$. Площади треугольников с общим углом относятся как произведения сторон, заключающих этот угол (см. рис. 6б):

$$ 2.<3>^<○>$$. Площади подобных треугольников относятся как квадраты их

сходственных сторон, т. е. если `Delta ABC

DeltaA_1B_1C_1`, то `(S_(A_1B_1C_1))/(S_(ABC))=((A_1B_1)/(AB))^2`.

Все эти утверждения легко доказываются с использованием соответственно формул площади (1) и (2).

Обратим внимание на важное свойство медиан треугольника.

Три медианы треугольника разбивают его на `6` треугольников с общей вершиной и равными площадями.

Известно, что три медианы треугольника пересекаются в одной точке и делятся в отношении `2:1`, считая от вершины. Пусть `O` – точка пересечения медиан треугольника `DeltaABC` площади `S` (рис. 7а). Надо доказать, что площади всех шести треугольников с верш иной в точке `O`, составляющих треугольник `ABC`, равны между собой, т. е. равны `1/6S`.

Докажем, например, для треугольника `BOM`, что `S_(BOM)=1/6S_(ABC)`.

Точка `M` – середина стороны `BC` (рис. 7б), по утверждению $$ 2.<1>^<○>$$ о сравнении площадей `S_(ABM)=1/2S`. Медиана `BN`, пересекая медиану `AM` в точке `O` (рис. 7в), делит её в отношении `AO:OM=2:1`, т. е. `OM=1/3AM`. По тому же утверждению $$ 2.<1>^<○>$$ площадь треугольника `BOM` составляет `1//3` площади треугольника `ABM`, т. е.

Дан треугольник `ABC`. Точка `D` лежит на стороне `AB`, `AD:DB=1:2`, точка `K` лежит на стороне `BC`, `BK:KC=3:2` (рис. 8а). Отрезки `AK` и `CD` пересекаются в точке `O`. Найти отношение площади четырёхугольника `DBKO` к площади треугольника `ABC`.

1. Обозначим `S_(ABC)=S`, `S_(DBKO)=sigma` и `S_(ADO)=a`. По утверждению $$ 2.<1>^<○>$$ имеем `S_(ABK)=a+sigma=3/5S` (так как `BK:BC=3:5`). Площадь `a` треугольника `ADO` найдём как часть площади треугольника `ADC`, зная, что `S_(ADC)=1/3S` (так как `AD:AB=1:3`).

2. Через точку `D` проведём прямую `DL“||“AK`. По теореме о пересечении сторон угла параллельными прямыми (`/_ABC`, `DL“||“AK`) имеем `(BL)/(LK)=(BD)/(AD)`, откуда `LK=y`.

По той же теореме (`/_DCB`, `OK“||“DL`) получим `(DO)/(DC)=(LK)/(LC)`, `DO=1/3DC`.

3. Теперь находим `S_(ADO):S_(ADC)=DO:DC`, `a=1/3(1/3S)=1/9S`.

(Можно по теореме Менелая для треугольника `BCD` и секущей `CD:`

`(BK)/(KC)*(CO)/(OD)*(DA)/(AB)=1 iff 3/2*(CO)/(OD)*1/3=1 iff CO=2OD=>OD=1/3DC`).

Находим площадь: `sigma=3/5S-a=(3/5-1/9)S=22/45S`.

Найти площадь треугольника, две стороны которого равны `3` и `7`, а медиана к третьей стороне равна `4` (рис. 9).

Пусть `AB=3`, `BC=7`, `AM=MC` и `BM=4`. Достроим треугольник `ABC` до параллелограмма, для этого на прямой `BM` отложим отрезок `MD=BM` и соединим точки: `A` с `D` и `C` с `D`. Противоположные стороны параллелограмма равны: `(DC=AB)` и равны площади треугольников `ABC` и `DBC` (общее основание `BC` и равные высоты из вершин `A` и `D`).

В треугольнике `DBC` известны все три стороны: `BC=7`, `DC=3`, `BD=2BM=8`.

Находим его площадь по формуле Герона: `p=9`, `S_(BCD)=6sqrt3`.

Значит и `S_(ABC)=6sqrt3`.

В решении этой задачи дополнительным построением получен треугольник, площадь которого равна площади заданного и легко вычисляется по данным задачи. Приведём ещё одну задачу, где сначала вычисляется площадь дополнительно построенной фигуры, а затем легко находится искомая площадь.

Найти площадь треугольника, если его медианы равны `3`, `4` и `5`.

Пусть `O` – точка пересечения медиан треугольника `ABC` (рис. 10) и пусть `m_a=AM=3`, `m_b=BN=4` и `m_c=CP=5`.

По свойству медиан `AO=2/3m_a`, `CO=2/3m_c` и `ON=1/3m_b`. В треугольнике `AOC` известны две стороны `AO` и `CO` и медиана третьей стороны `ON`. Площадь этого треугольника найдём как в предыдущей задаче.

Достроим треугольник `AOC` до параллелограмма `AOCD`, `S_(AOC)=S_(DOC)`, в треугольнике `DOC` известны три стороны:

`DO=2ON=2/3m_b`, `OC=2/3m_c`, `DC=AO=2/3m_a`.

Площадь треугольника `DOC` вычисляем по формуле Герона `S_1=S_(AOC)=S_(DOC)=8/3`. Сравним теперь площадь треугольника `ABC` (обозначим её `S`) с площадью треугольника `AOC`. Из теоремы 2 о медианах и площадях следует `S_(AOC)=S_(AON)+S_(NOC)=2*1/6S=1/3S`.

В следующей задаче докажем лемму об отношении площади треугольника к площади другого треугольника, построенного из медиан первого.

Найти отношение площади `S` треугольника к площади `S_0` треугольника, составленного из медиан первого.

Рассмотрим рис. 10. В построенном треугольнике `OCD` стороны таковы: `OC=2/3m_c`, `OD=2/3m_b`, `CD=2/3m_a`. Очевидно, что треугольник со сторонами `m_a`, `m_b`, `m_c` подобен (по третьему признаку) треугольнику со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`.

Из решения предыдущей задачи следует, что `S_(OCD)=S_1=1/3S` (здесь `S` – площадь треугольника `ABC`). Кроме того, площади подобных треугольников относятся как квадраты сходственных сторон, поэтому `(S_1)/(S_0)=(2/3)^2`. Таким образом, имеем `S_0=9/4S_1=3/4S`, т. е.

`S_(m_am_bm_c)=3/4S_(abc)`.

Из рассуждений в решении Примера 9 следует, что всегда существует треугольник со сторонами, равными медианам данного треугольника, поскольку всегда существует подобный ему треугольник со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`. Кроме того, становится ясным план построения треугольника по трём отрезкам, равным его медианам: сначала строится треугольник `OCD` (см. рис. 10) со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`, затем точка `N` – середина отрезка `OD`, потом точка `A` (из `AN=NC`) и точка `B` (из `OB=OD`). Это построение осуществимо, если существует треугольник `OCD`, т. е. если существует треугольник со сторонами `m_a`, `m_b`, `m_c`. Итак, вывод: три отрезка могут быть медианами некоторого треугольника тогда и только тогда, когда из них можно составить треугольник.

Около окружности радиуса `sqrt3` описан треугольник. Найти его площадь, если одна из его сторон точкой касания делится на отрезки `9` и `5`.

Пусть `AP=9`, `PC=5` (рис. 11) и пусть `BM=x`. По свойству касательных `AM=AP`, `CN=CP` и `BN=BM`, поэтому стороны треугольника таковы: `AC=14`, `AB=9+x`, `BC=5+x`, тогда `p=14+x`. (Заметим, что `p=AC+BM`!). По формулам площади (3) и (4) имеем: `S=pr=(14+x)sqrt3` и `S=sqrt((14+x)x*5*9)`. Приравниваем правые части, возводим в квадрат, приводим подобные члены, получаем `x=1`. Вычисляем площадь треугольника:

Приём, применённый в решении этой задачи, когда площадь фигуры выражается двумя различными способами, часто используется в задачах на доказательство.

Проведём два примера, в каждом выведем полезную формулу.

В треугольнике `ABC` угол `C` равен `varphi`, `AC=b`, `BC=a` (рис. 12). Доказать, что биссектриса `CD` равна `(2ab)/(a+b) cos varphi/2`.

Обозначим `CD=x`. Очевидно, что `S_(ABC)=S_(ACD)+S_(DCB)`. По формуле (2) `S_(ABC)=1/2 ab sin varphi`, `S_(ACD)=1/2 bx sin varphi/2`, `S_(BDC)=1/2 ax sin varphi/2`. Таким образом, имеем: `1/2 ab sin varphi=1/2(a+b)x sin varphi/2`. Используем формулу синуса двойного угла `sin varphi=2sin varphi/2 cos varphi/2`, получим:

`x=(2ab)/(a+b)cos varphi/2`.

называется окружность, касающаяся одной из сторон треугольника и продолжений двух других сторон. Таких окружностей, очевидно, три (рис. 13). Их радиусы обычно обозначаются `r_a`, `r_b`, `r_c` в зависимости от того, какой стороны окружность касается.

Вневписанная окружность касается стороны `a=BC` треугольника `ABC` (рис. 14). Доказать, что `S_(ABC)=r_a(p-a)`, где `2p=a+b+c`.

Центр окружности `I_a` лежит на пересечении биссектрисы угла `A` и биссектрис внешних углов при вершинах `B` и `C`. Легко видеть, что если `D`, `F` и `E` – точки касания, то `I_aD=I_aF=I_aE=r_a`.

Считаем площадь `S_0` четырёхугольника `ABI_aC`:

`S_0=S_(ABC)+S_(BCI_a)` и `S_0=S_(ABI_a)+S_(ACI_a)`, откуда

Как найти площадь треугольника

О чем эта статья:

Основные понятия

Треугольник — это геометрическая фигура, которая получилось из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.

Площадь — это численная характеристика, которая дает нам информацию о размере плоскости, ограниченной замкнутой геометрической фигурой.

Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

Популярные единицы измерения

квадратный миллиметр (мм 2 );
квадратный сантиметр (см 2 );
квадратный дециметр (дм 2 );
квадратный метр (м 2 );
квадратный километр (км 2 );
гектар (га).

Формула площади треугольника

Для решения задач применяются различные формулы, в зависимости от известных исходных данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.

Быстро вычислить площадь треугольника поможет наш онлайн-калькулятор. Просто введите известные вам значения и получите ответ в метрах, сантиметрах или миллиметрах.

Общая формула

1. Площадь треугольника через две стороны и угол между ними.

S = 0,5 * a * b⋅sin(α) , где a, b — стороны, α — угол между ними.

2. Площадь треугольника через основание и высоту.

S = 0,5 * a * h, где a — основание, h — высота.

3. Площадь треугольника через описанную окружность и стороны.

S = (a * b * c) : (4 * R), где a, b, c — стороны, R — радиус описанной окружности.

4. Площадь треугольника через вписанную окружность и стороны.

S = r * (a + b + c) : 2, где a, b, c — стороны, r — радиус вписанной окружности.

Если учитывать, что (a + b + c) : 2 — это способ поиска полупериметра. Тогда формулу можно записать следующим образом:

S = r * p, где p — полупериметр.

5. Площадь треугольника по стороне и двум прилежащим углам.

S = a 2 : 2 * (sin(α)⋅sin(β)) : sin(180 — (α + β)), где a — сторона, α и β — прилежащие углы, γ — противолежащий угол.

6. Формула Герона для вычисления площади треугольника.

Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.

Читайте также:

Формулы площадей всех фигур

S = √ p * (p − a) * (p − b) * (p − c), где a, b, c — стороны, p — полупериметр, который можно найти по формуле: p = (a + b + c) : 2

Для прямоугольного треугольника

Площадь треугольника с углом 90° по двум сторонам.

S = 0,5 * a * b, где a, b — стороны.

Площадь треугольника по гипотенузе и острому углу.

S = 0,25 * c 2 * sin(2α), где c — гипотенуза, α — любой из прилегающих острых углов.

Гипотенузой принято называть сторону, которая лежит напротив прямого угла.

Площадь прямоугольного треугольника по катету и прилежащему углу.

S = 0,5 * a 2 * tg(α), где a — катет, α — прилежащий угол.

Катетом принято называть одну из двух сторон, образующих прямой угол.

Площадь треугольника через гипотенузу и по радиусу вписанной окружности.

S = r * (r + c), где c — гипотенуза, r — радиус вписанной окружности.

Площадь треугольника вписанного в окружность.

Площадь прямого треугольника по формуле Герона.

S = (p − a) * (p − b), где a, b — катеты, p — полупериметр, который рассчитывается по формуле p = (a + b + c) : 2.

Для равнобедренного треугольника

Поиск площади через основание и сторону.

S = b : 4 * √ 4 * a 2 − b 2 , где a — боковая сторона, b — основание.

Вычисление площади через основание и угол.

S = 0,5 * a * b * sin(α), где a — боковая сторона, b — основание, α — угол между основанием и стороной.

Вычисление площади через основание и высоту.

S = 0,5 * b * h, где b — основание, h — высота, проведенная к основанию.

Поиск площади через боковые стороны и угол между ними.

S = 0,5 * a 2 * sin(α), где a — боковая сторона, α — угол между боковыми сторонами.

Площадь равнобедренного треугольника через основание и угол между боковыми сторонами.

S = b 2 : (4 * tgα/2), где b — основание, α — угол между боковыми сторонами.

Площадь равностороннего треугольника через радиус описанной окружности.

S = (3 * √ 3 * R 2 ) : 4, где R — радиус описанной окружности.

Площадь равностороннего треугольника через радиус вписанной окружности.

S = 3 * √ 3 * r 2 , где r — радиус вписанной окружности.

Площадь равностороннего треугольника через сторону.

S = (√ 3 * a 2 ) : 4, где a — сторона.

Площадь равностороннего треугольника через высоту.

S = h 2 : √ 3, где h — высота.

Таблица формул нахождения площади треугольника

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Площадь треугольника

Формулы для площади треугольника

Вывод формул для площади произвольного треугольника

Вывод формул для площади равностороннего (правильного) треугольника

Вывод формул для площади прямоугольного треугольника

Формулы для площади треугольника

Формулы, позволяющие находить площадь треугольника , удобно представить в виде следующей таблицы.

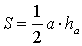
a – любая сторона,
h_a – высота, опущенная на эту сторону

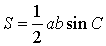
a и b – две любые стороны,
С – угол между ними

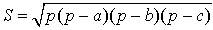
Формулу называют «Формула Герона»

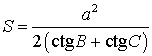
a – любая сторона,
B, С – прилежащие к ней углы

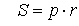
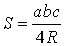
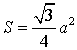
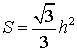
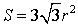
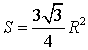
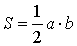
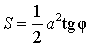
a – катет,
φ – прилежащий острый угол

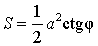
a – катет,
φ – противолежащий острый угол

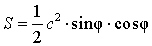
c – гипотенуза,
φ – любой из острых углов

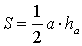
где
a – любая сторона,
h_a – высота, опущенная на эту сторону

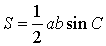
где
a и b – две любые стороны,
С – угол между ними

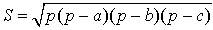
Формулу называют «Формула Герона»

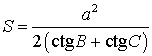
где
a – любая сторона,
B, С – прилежащие к ней углы

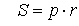
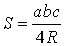
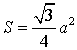
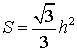
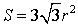
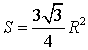
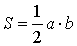
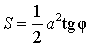
где
a – катет,
φ – прилежащий острый угол

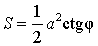
где
a – катет,
φ – противолежащий острый угол

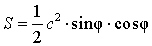
где
c – гипотенуза,
φ – любой из острых углов

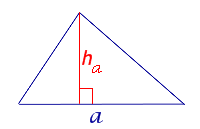
Произвольный треугольник

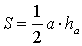
где
a – любая сторона,
h_a – высота, опущенная на эту сторону

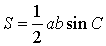
где
a и b – две любые стороны,
С – угол между ними

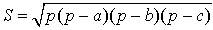
Формулу называют «Формула Герона»

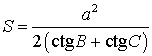
где
a – любая сторона,
B, С – прилежащие к ней углы

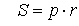
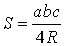
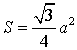
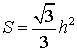
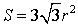
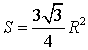
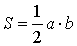
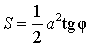
где
a – катет,
φ – прилежащий острый угол

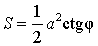
где
a – катет,
φ – противолежащий острый угол

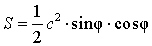
где
c – гипотенуза,
φ – любой из острых углов

Вывод формул для площади произвольного треугольника

Утверждение 1 . Площадь треугольника можно найти по формуле

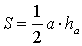
где a – любая сторона треугольника, а h_a – высота, опущенная на эту сторону.

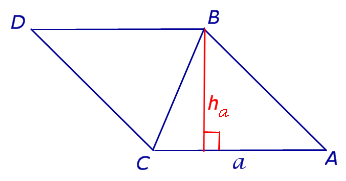
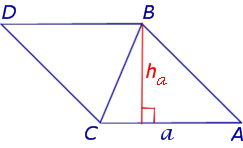
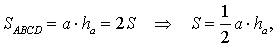
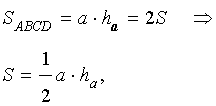
что и требовалось доказать.

Утверждение 2 . Площадь треугольника можно найти по формуле

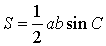
где a и b – две любые стороны треугольника, а С – угол между ними.

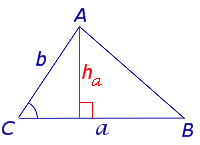
то, в силу утверждения 1, справедлива формула

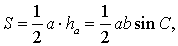
что и требовалось доказать.

Утверждение 3 . Площадь треугольника можно найти по формуле

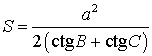
где a – любая сторона треугольника, а B, С – прилежащие к ней углы.

Замечание . Докажем утверждение 3 в случае остроугольного треугольника. Доказательство в случаях прямоугольного и тупоугольного треугольников требует лишь незначительных изменений, совершить которые мы предоставляем читателю в качестве самостоятельного упражнения.

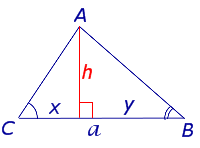
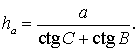
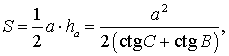
что и требовалось доказать.

Утверждение 4 . Площадь треугольника можно найти по формуле

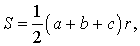
где a, b, c – стороны треугольника, а r – радиус вписанной окружности.

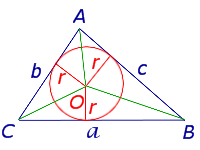
Соединив центр O вписанной окружности с вершинами треугольника (рис.4), получим

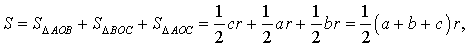
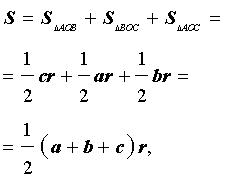
что и требовалось доказать.

Утверждение 5 . Площадь треугольника можно найти по формуле

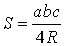
где a, b, c – стороны треугольника, а R – радиус описанной окружности.

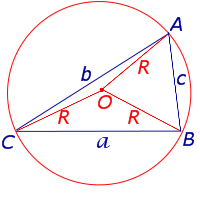
В силу теоремы синусов справедливо равенство

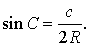
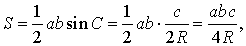
что и требовалось доказать.

Утверждение 6 . Площадь треугольника можно найти по формуле:

где A, B, С – углы треугольника, а R – радиус описанной окружности.

В силу теоремы синусов справедливо равенство

В силу утверждения 5

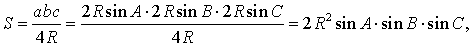
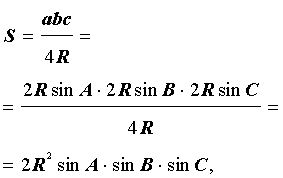
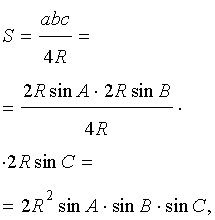
что и требовалось доказать.

Вывод формул для площади равностороннего треугольника

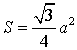
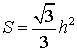
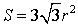
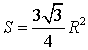
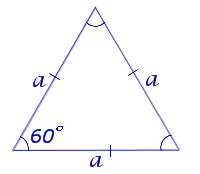
В силу утверждения 2

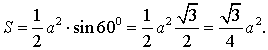
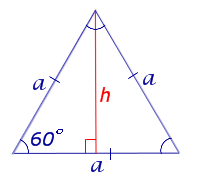
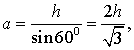
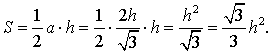
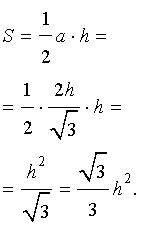
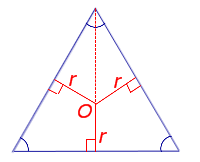
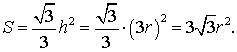
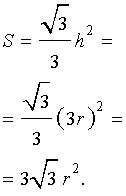
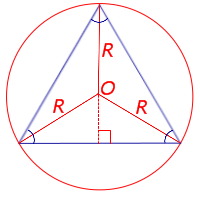
Поскольку у равностороннего треугольника центр описанной окружности совпадает с точкой пересечения медиан, высот и биссектрис, то выполнено равенство 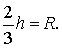Следовательно,

Площадь треугольника — формулы и калькулятор онлайн

Задача нахождения площади треугольника довольно распространена не только в науке, но и в быту. Для вас мы разработали 21 калькулятор для нахождения площади любого треугольника — равнобедренного, равностороннего, прямоугольного или обыкновенного.

Площадь треугольника

Площадь треугольника через две стороны и угол между ними

<2>cdot a cdot b cdot sin (alpha)>

Формула для нахождения площади треугольника через 2 стороны и угол:

<2>cdot a cdot b cdot sin (alpha)> , где a, b — стороны треугольника, α — угол между ними.

Площадь треугольника через основание и высоту

Формула для нахождения площади треугольника через основание и высоту:

<2>cdot a cdot h> , где a — основание треугольника, h — высота треугольника.

Площадь треугольника через радиус описанной окружности и 3 стороны

Формула для нахождения площади треугольника через описанную окружность и стороны:

<4 cdot R>> , где a, b, c — стороны треугольника, R — радиус описанной окружности.

Площадь треугольника через радиус вписанной окружности и 3 стороны

Формула для нахождения площади треугольника через вписанную окружность и стороны:

<2>> , где a, b, c — стороны треугольника, r — радиус вписанной окружности.

Формулу можно переписать иначе, если учитывать, что <2>> — полупериметр треугольника. В этом случае формула будет выглядеть так: S = , где p — полупериметр треугольника.

Площадь треугольника через сторону и два прилежащих угла

Формула для нахождения площади треугольника через сторону и 2 прилежащих угла:

<2>cdot dfrac> , где a — сторона треугольника, α и β — прилежащие углы, γ — противолежащий угол, который можно найти по формуле:

Площадь треугольника по формуле Герона

Формула для нахождения площади треугольника по формуле Герона (если известны 3 стороны):

> , где a, b, c — стороны треугольника, p — полупериметр треугольника, который можно найти по формуле p = <2>>

Площадь прямоугольного треугольника

Площадь прямоугольного треугольника через 2 стороны

Формула для нахождения площади прямоугольного треугольника по двум сторонам:

<2>cdot a cdot b> , где a, b — стороны треугольника.

Площадь прямоугольного треугольника через гипотенузу и острый угол

<4>cdot c^2 cdot sin (2 alpha)>

Формула для нахождения площади прямоугольного треугольника по гипотенузе и острому углу:

<4>cdot c^2 cdot sin (2 alpha)> , где c — гипотенуза треугольника, α — любой из прилегающих острых углов.

Площадь прямоугольного треугольника через катет и прилежащий угол

Формула для нахождения площади прямоугольного треугольника по катету и прилежащему углу:

<2>cdot a^2 cdot tg (alpha)> , где a — катет треугольника, α — прилежащий угол.

Площадь прямоугольного треугольника через радиус вписанной окружности и гипотенузу

Формула для нахождения площади прямоугольного треугольника по радиусу вписанной окружности и гипотенузе:

, где c — гипотенуза треугольника, r — радиус вписанной окружности.

Площадь прямоугольного треугольника через вписанную окружность

Формула для нахождения площади прямоугольного треугольника по вписанной окружности:

cdot c_<2>> , где c₁ и c₂ — части гипотенузы.

Площадь прямоугольного треугольника по формуле Герона

Формула Герона для прямоугольного треугольника выглядит так:

, где a, b — катеты треугольника, p — полупериметр прямоугольного треугольника, который рассчитывается по формуле p = <2>>

Площадь равнобедренного треугольника

Площадь равнобедренного треугольника через основание и сторону

Формула площади равнобедренного треугольника через основание и сторону:

<4>sqrt<4 cdot a^2-b^2>> , где a — боковая сторона треугольника, b — основание треугольника

Площадь равнобедренного треугольника через основание и угол

<2>cdot a cdot b cdot sin( alpha)>

Формула площади равнобедренного треугольника через основание и угол:

<2>cdot a cdot b cdot sin( alpha)> , где a — боковая сторона треугольника, b — основание треугольника, α — угол между основанием и стороной.

Площадь равнобедренного треугольника через основание и высоту

Формула площади равнобедренного треугольника через основание и высоту:

<2>cdot b cdot h> , где b — основание треугольника, h — высота, проведенная к основанию.

Площадь равнобедренного треугольника через боковые стороны и угол между ними

Формула площади равнобедренного треугольника через боковые стороны и угол между ними:

<2>cdot a^2 cdot sin(alpha)> , где a — боковая сторона треугольника, α — угол между боковыми сторонами.

Площадь равнобедренного треугольника через основание и угол между боковыми сторонами

Формула площади равнобедренного треугольника через основание и угол между боковыми сторонами:

<4 cdot tg dfrac<2>>> , где b — основание треугольника, α — угол между боковыми сторонами.

Площадь равностороннего треугольника

Площадь равностороннего треугольника через радиус описанной окружности

Формула площади равностороннего треугольника через радиус описанной окружности:

cdot R^2><4>> , где R — радиус описанной окружности.

Площадь равностороннего треугольника через радиус вписанной окружности

Формула площади равностороннего треугольника через радиус вписанной окружности:

cdot r^2> , где r — радиус вписанной окружности.

Площадь равностороннего треугольника через сторону

Формула площади равностороннего треугольника через сторону:

cdot a^2><4>> , где a — сторона треугольника.

Площадь равностороннего треугольника через высоту

Формула площади равностороннего треугольника через высоту:

>> , где h — высота треугольника.

Треугольник

Треугольник — фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.

типы треугольников
вершины углы и стороны треугольника
медианы треугольника
биссектрисы треугольника
высоты треугольника
окружность вписанная в треугольник
окружность описанная вокруг треугольника
связь между вписанной и описанной окружностями треугольника
средняя линия треугольника
периметр треугольника
формулы площади треугольника
равенство треугольников
подобие треугольников
прямоугольные треугольники

Типы треугольников

По величине углов

Остроугольный треугольник

— все углы треугольника острые.

Тупоугольный треугольник

— один из углов треугольника тупой (больше 90°).

Прямоугольный треугольник

— один из углов треугольника прямой (равен 90°).

По числу равных сторон

Разносторонний треугольник

— все три стороны не равны.

Равнобедренный треугольник

— две стороны равны.

Равносторонний (правильный) треугольник

— все три стороны равны.

Вершины, углы и стороны треугольника

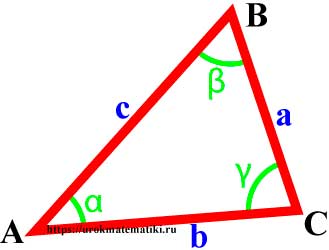
Свойства углов и сторон треугольника

Сумма углов треугольника равна 180°

В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы

если α > β , тогда a > b
если α = β , тогда a = b

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов.

a sin α = b sin β = c sin γ

Теорема косинусов

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведение этих сторон на косинус угла между ними.

a 2 = b 2 + c 2 – 2 b c · cos α
b 2 = a 2 + c 2 – 2 a c · cos β
c 2 = a 2 + b 2 – 2 a b · cos γ

Теорема о проекциях

Для остроугольного треугольника:

a = b cos γ + c cos β
b = a cos γ + c cos α;
c = a cos β + b cos α;

Формулы для вычисления длин сторон треугольника

Формулы сторон через медианы

a = 2 3 2 m b 2 + m c 2 – m a 2

b = 2 3 2 m a 2 + m c 2 – m b 2

c = 2 3 2 m a 2 + m b 2 – m c 2

Медианы треугольника

Медиана треугольника — отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.

Свойства медиан треугольника

Медианы треугольника пересекаются в одной точке. Точка пересечения медиан называется центроидом.

В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
AO OD = BO OE = CO OF = 2 1

Медиана треугольника делит треугольник на две равновеликие части

Треугольник делится тремя медианами на шесть равновеликих треугольников

S ∆AOF = S ∆AOE = S ∆BOF = S ∆BOD = S ∆COD = S ∆COE

Из векторов, образующих медианы, можно составить треугольник

Формулы медиан треугольника

Формулы медиан треугольника через стороны

m a = 1 2 2 b 2 + 2 c 2 – a 2

m b = 1 2 2 a 2 + 2 c 2 – b 2

m c = 1 2 2 a 2 + 2 b 2 – c 2

Биссектрисы треугольника

Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.

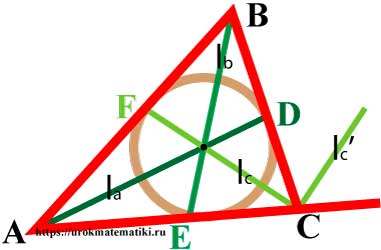
Свойства биссектрис треугольника

Биссектрисы треугольника пересекаются в одной точке, равноудаленной от трех сторон треугольника, – центре вписанной окружности.

Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
AE AB = EC BC

Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°

Угол между l c и l c ‘ = 90°

Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный.

Формулы биссектрис треугольника

Формулы биссектрис треугольника через стороны

l a = 2 b c p p – a b + c

l b = 2 a c p p – b a + c

l c = 2 a b p p – c a + b

где p = a + b + c 2 — полупериметр треугольника.

Формулы биссектрис треугольника через две стороны и угол

l a = 2 b c cos α 2 b + c

l b = 2 a c cos β 2 a + c

l c = 2 a b cos γ 2 a + b

Высоты треугольника

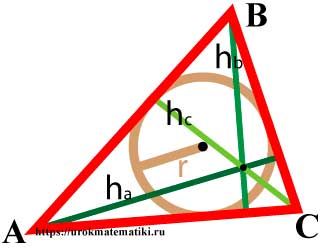
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону.

В зависимости от типа треугольника высота может содержаться:

внутри треугольника — для остроугольного треугольника;
совпадать с его стороной — для катета прямоугольного треугольника;
проходить вне треугольника — для острых углов тупоугольного треугольника.

Свойства высот треугольника

Высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.

Если в треугольнике две высоты равны, то треугольник — равнобедренный.

h a : h b : h c = 1 a : 1 b : 1 c = BC : AC : AB

1 h a : 1 h b : 1 h c = 1 r

Формулы высот треугольника

Формулы высот треугольника через сторону и угол

h a = b sin γ = c sin β

h b = c sin α = a sin γ

h c = a sin β = b sin α

Формулы высот треугольника через сторону и площадь

Формулы высот треугольника через две стороны и радиус описанной окружности

Окружность вписанная в треугольник

Окружность называется вписанной в треугольник, если она касается всех трех его сторон.

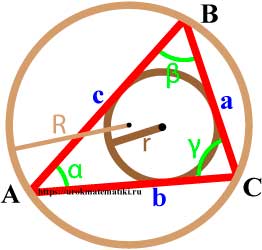
Свойства окружности вписанной в треугольник

Центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника.
В любой треугольник можно вписать окружность, и только одну.

Формулы радиуса окружности вписанной в треугольник

Радиус вписанной в треугольник окружности равен отношению площади треугольника к его полупериметру

Радиус вписанной в треугольник окружности через три стороны

Формулы высот треугольника через две стороны и радиус описанной окружности

Окружность описанная вокруг треугольника

Окружность называется описанной вокруг треугольника, если она содержит все вершины треугльника.

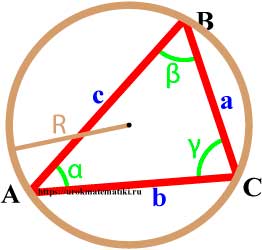
Свойства окружности описанной вокруг треугольника

Центр описанной вокруг треугольника окружности лежит на пересечении серединных перпендикуляров к его сторонам.
Вокруг любого треугольника можно описать окружность, и только одну.

Свойства углов

Центр описанной окружности лежит внутри остроугольного треугольника, снаружи тупоугольнго треугольника, на середине гипотенузы прямоугольного треугольника.

Формулы радиуса окружности описанной вокруг треугольника

Радиус описанной окружности через три стороны и площадь

Радиус описанной окружности через площадь и три угла

Радиус описанной окружности через сторону и противоположный угол (теорема синусов)

Связь между вписанной и описанной окружностями треугольника

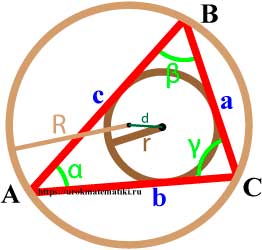
Формулы радиуса окружности описанной вокруг треугольника

Если d — расстояние между центрами вписанной и описанной окружностей, то

d 2 = R 2 – 2 R r

Радиус описанной окружности через площадь и три угла

Средняя линия треугольника

Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.

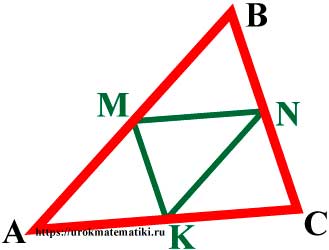
Свойства средней линии треугольника

Любой треугольник имеет три средних линии.
Средняя линия треугольника параллельна основанию и равна его половине.
MN = 1 2 AC ; KN = 1 2 AB ; KM = 1 2 BC

MN || AC ; KN || AB ; KM || BC

Средняя линия отсекает треугольник, подобный данному, площадь которого равна четвёрти площади исходного треугольника.
S ∆MBN = 1 4 S ∆ABC ; S ∆MAK = 1 4 S ∆ABC ; S ∆NCK = 1 4 S ∆ABC

При пересечении всех трёх средних линий образуются 4 равных треугольника, подобных (даже гомотетичных) исходному с коэффициентом 1/2.
∆MBN

Признаки

Если отрезок параллелен одной из сторон треугольника и соединяет середину стороны треугольника с точкой, лежащей на другой стороне треугольника, то этот отрезок — средняя линия.

Периметр треугольника

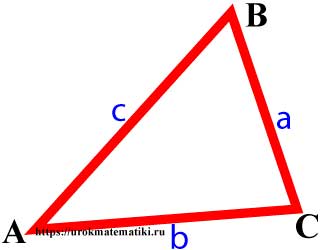
Периметр треугольника ∆ABC равен сумме длин его сторон.

Формулы площади треугольника

Формула площади треугольника по стороне и высоте

Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.

S = 1 2 a · h a ,
S = 1 2 b · h b ,
S = 1 2 c · h c ,

где a, b, c — стороны треугольника,
h_a, h_b, h_c — высоты, проведенные к сторонам a, b, c треугольника.

Формула площади треугольника по трем сторонам

Формула Герона формула для вычисления площади треугольника S по длинам его сторон a, b, c .

S = p p – a p – b p – c ,

где p — полупериметр треугольника: p = a + b + c 2
a, b, c — стороны треугольника.

Формула площади треугольника по двум сторонам и углу между ними

Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.

S = 1 2 a · b · sin γ ,
S = 1 2 b · c · sin α ,
S = 1 2 a · c · sin β ,

где a, b, c — стороны треугольника,
γ — угол между сторонами a и b ,
α — угол между сторонами b и c ,
β — угол между сторонами a и c .

Формула площади треугольника по трем сторонам и радиусу описанной окружности

a, b, c — стороны треугольника,
R – радиус описанной окружности.

Формула площади треугольника по трем сторонам и радиусу вписанной окружности

Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

где S — площадь треугольника,
r – радиус вписанной окружности,
p — полупериметр треугольника: p = a + b + c 2

Равенство треугольников

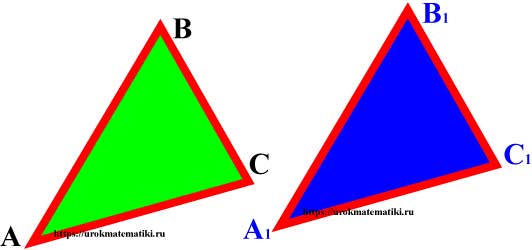
Определение

Если два треугольника АВС и А₁В₁С₁ можно совместить наложением, то они равны.

Свойства

У равных треугольников равны и их соответствующие элементы. (В равных треугольниках против равных сторон лежат равные углы, против равных углов лежат равные стороны).

Признаки равенства треугольников

По двум сторонам и углу между ними

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

По стороне и двум прилежащим углам

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

По трем сторонам

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Подобие треугольников

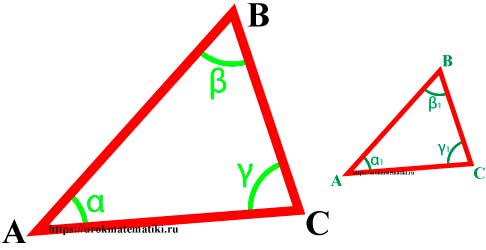
Определение

Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.

∆MNK => α = α 1 , β = β 1 , γ = γ 1 и AB MN = BC NK = AC MK = k

где k — коэффициент подобия.

Признаки подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
Если две стороны одного треугольника пропорциональны двум сторонам другого, а углы, между этими сторонами, равны, то такие треугольники подобны.

Свойства

Площади подобных треугольников относятся как квадрат коэффициента подобия:

S ∆АВС S ∆MNK = k 2

Прямоугольные треугольники

Прямоугольный треугольник — треугольник, в котором один угол прямой (то есть равен 90˚).

Свойства прямоугольного треугольника

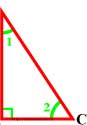
Сумма двух острых углов прямоугольного треугольника равна 90°.
Сумма углов треугольника равна 180°, а прямой угол равен 90°, поэтому сумма двух острых углов прямоугольного треугольника ∡1 + ∡2 = 90° .

Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы (гипотенуза в два раза длиннее катета, лежащего против угла в 30°).

Рассмотрим прямоугольный треугольник ABC, в котором ∡A — прямой, ∡B = 30°, и значит, что ∡C = 60°.

Докажем, что BC=2AC.
Приложим к треугольнику ABC равный ему треугольник ABD , как показано на рисунке.
Получим треугольник BCD, в котором ∡B = ∡D = 60° , поэтому DC = BC. Но DC = 2AC. Следовательно, BC = 2AC.

Справедливо и обратное суждение: Если катет прямоугольного треугольника равен половине гипотенузы (или гипотенуза в два раза длиннее катета), то угол, лежащий против этого катета, равен 30°.

Признаки равенства прямоугольных треугольников

Так как в прямоугольном треугольнике угол между двумя катетами — прямой, а любые два прямых угла равны, то из общих признаков равенства треугольников для прямоугольных треугольников можно сформулировать свои признаки равенства.

Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.

Свойства

Площади подобных треугольников относятся как квадрат коэффициента подобия:

Как найти площадь треугольника

На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.

Треугольник – это многоугольник с тремя сторонами.

По формуле Герона

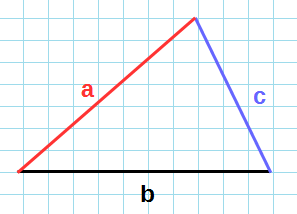
Формула Герона для нахождения площади треугольника:

Через основание и высоту

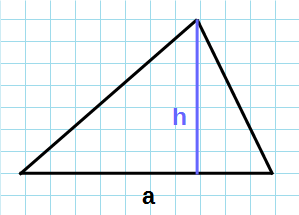
Формула нахождения площади треугольника с помощью половины его основания и высоту:

Через две стороны и угол

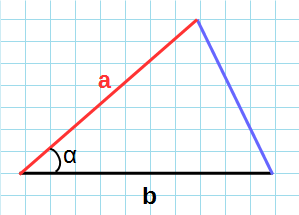
Формула нахождения площади треугольника через две стороны и угол между ними:

Через сторону и два прилежащих угла

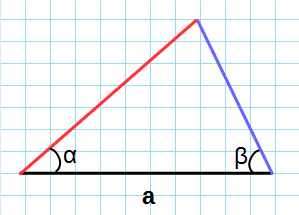
Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:

Площадь прямоугольного треугольника

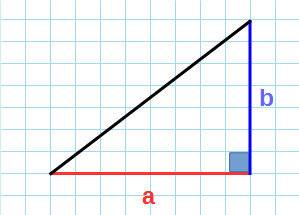
Прямоугольный треугольник – треугольник у которого один из углов прямой, т.е. равен 90°.

Формула нахождения площади прямоугольного треугольника через катеты:

Площадь равнобедренного треугольника через стороны

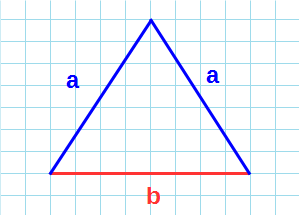
Равнобедренный треугольник – треугольник, в котором две стороны равны. А значит, равны и два угла.

Формула нахождения площади равнобедренного треугольника через две стороны:

Площадь равнобедренного треугольника через основание и угол

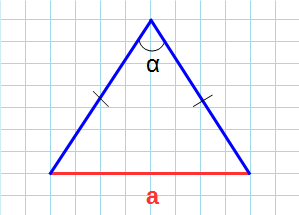
Формула нахождения площади равнобедренного треугольника через основание и угол:

Площадь равностороннего треугольника через стороны

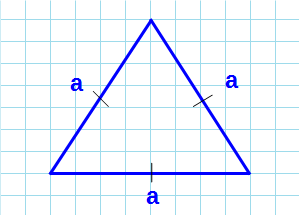
Равносторонний треугольник – треугольник, в котором все стороны равны, а каждый угол равен 60°.

Формула нахождения площади равностороннего треугольника через сторону:

Площадь равностороннего треугольника через высоту

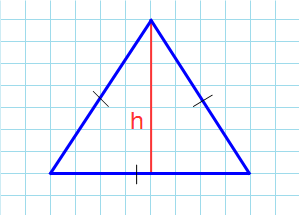
Формула нахождения площади равностороннего треугольника через высоту:

Площадь равностороннего треугольника через радиус вписанной окружности

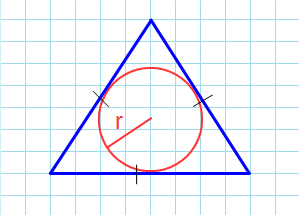
Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:

Площадь равностороннего треугольника через радиус описанной окружности

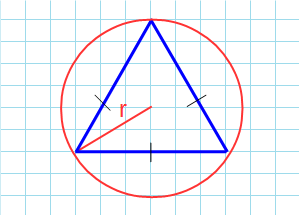
Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:

Площадь треугольника через радиус описанной окружности и три стороны

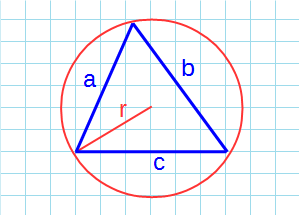
Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:

Площадь треугольника через радиус вписанной окружности и три стороны

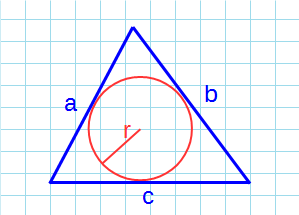
Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:

Площадь треугольника – определение и вычисление с примерами решения

Площадь треугольника:

Теорема (о площади треугольника). Площадь треугольника равна половине произведения его стороны на высоту, к ней проведенную.

Доказательство:

Пусть

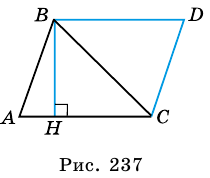
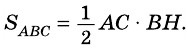
1) Проведем через вершину 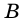прямую, параллельную 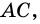а через вершину 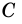– прямую, параллельную 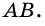Получим параллелограмм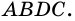

2) 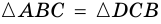(по трем сторонам). Поэтому

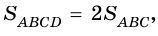откуда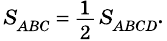

3) Так как 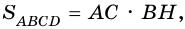то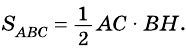

В общем виде формулу площади 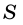треугольника можно записать так:

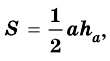
где 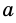– сторона треугольника, 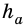– высота, проведенная к ней.

Следствие 1. Площадь прямоугольного треугольника равна половине произведения катетов.

Следствие 2. Если сторона одного треугольника равна стороне другого треугольника, то площади таких треугольников относятся как их высоты, проведенные к этим сторонам.

Следствие 3. Если высота одного треугольника равна высоте другого треугольника, то площади этих треугольников относятся как стороны, к которым проведены эти высоты.

Пример:

Докажите, что если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, образующих этот угол.

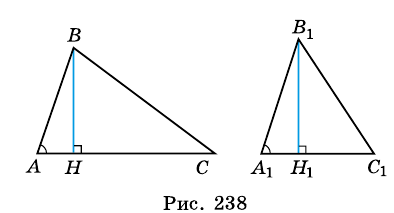
Доказательство:

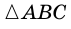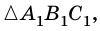Рассмотрим и у которых 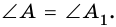Проведем высоты 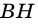и 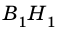(рис. 238).

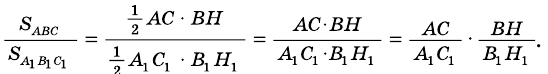
2) 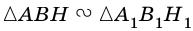(по острому углу), поэтому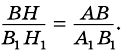

3) Имеем: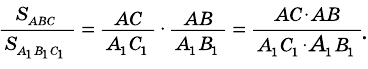

Пример:

Найдите площадь равностороннего треугольника, сторона которого равна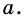

Решение:

Пусть 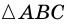– равносторонний со стороной 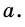Тогда 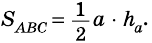В равностороннем треугольник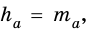е где 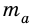– медиана. Но 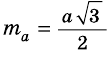(§ 18, задача 4), поэтому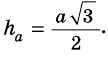

Следовательно,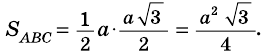

Ответ.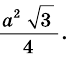

Пример:

Стороны треугольника равны 8 см, 15 см и ^ 17 см. Найдите высоту треугольника, проведенную к его наибольшей стороне.

Решение:

Так как 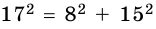(т. е. 289 = 289), то по теореме, обратной теореме Пифагора, треугольник является прямоугольным. Прямой угол является противолежащим к стороне, равной 17 см.

Пусть на рис. 239 изображен прямоугольный треугольник, у которого 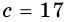см -гипотенуза, 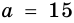и 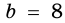см – катеты, 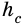– высота. Найдем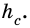

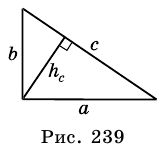
Площадь этого треугольника можно найти

по формулам: 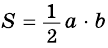или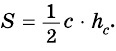

Тогда 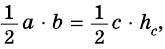то есть 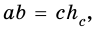откуда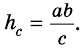

Таким образом, имее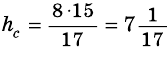м: (см).

Ответ. 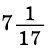см.

Теорема (формула площади треугольника)

Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне:

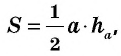
где 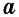— сторона треугольника, 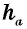— проведенная к ней высота.

Пусть 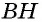— высота треугольника 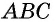(рис. 148). Докажем, что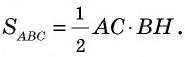

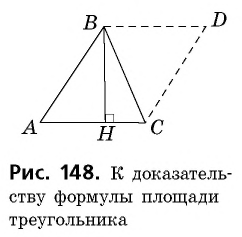
Проведем через вершины 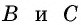прямые, параллельные сторонам треугольника, и обозначим точку их пересечения 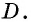Таким образом, мы «достроили» треугольник 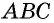до параллелограмма 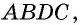в котором отрезок 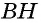также является высотой, проведенной к стороне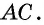

По формуле площади параллелограмма 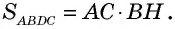Треугольники 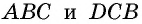равны по трем сторонам (у них сторона 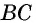общая, 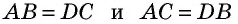как противолежащие стороны параллелограмма). Эти треугольники имеют равные площади. Тогда площадь треугольника 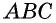составляет половину площади параллелограмма 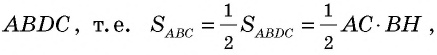что и требовалось доказать.

Следствие 1

Площадь прямоугольного треугольника равна половине произведения его катетов:

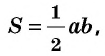
где 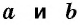— катеты прямоугольного треугольника.

Действительно, в прямоугольном треугольнике высота, проведенная к катету, совпадает с другим катетом.

Следствие 2

Площадь ромба равна половине произведения его диагоналей:

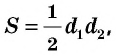
где 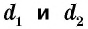— диагонали ромба.

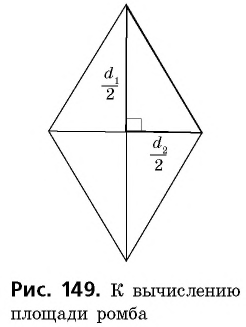
Действительно, диагонали делят ромб на четыре равных прямоугольных треугольника с катетами 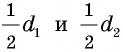(рис. 149). Используя следствие 1, имеем:

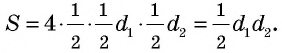
Следствие 3

Площадь равностороннего треугольника со стороной 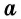вычисляется по формуле

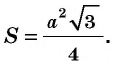
Обоснуйте это следствие самостоятельно.

Опорная задача

Медиана делит треугольник на два равновеликих треугольника. Докажите.

Решение:

Пусть 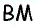— медиана треугольника 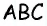(рис. 150).

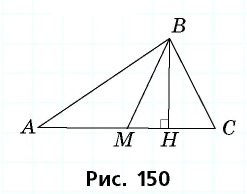
Проведем высоту 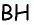треугольника 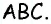Этот отрезок является одновременно высотой треугольника 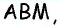проведенной к стороне 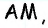и высотой треугольника 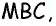проведенной к стороне 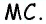Учитывая равенство отрезков 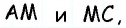имеем:

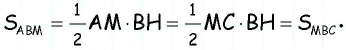
Эта задача имеет интересные обобщения: если высоты двух треугольников равны, то отношение площадей этих треугольников равно отношению их оснований; если основания двух треугольников равны, то отношение площадей этих треугольников равно отношению их высот.

Докажите эти утверждения самостоятельно.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.