Усеченные пирамиды. Теорема Эйлера. Формулы для объема, площади боковой поверхности и площади полной поверхности усеченной пирамиды
 Усеченные пирамиды. Теорема Эйлера для усеченных пирамид Усеченные пирамиды. Теорема Эйлера для усеченных пирамид |
 Правильные усеченные пирамиды Правильные усеченные пирамиды |
 Формулы для объема, площади боковой поверхности и площади полной поверхности усеченной пирамиды Формулы для объема, площади боковой поверхности и площади полной поверхности усеченной пирамиды |

Усеченные пирамиды
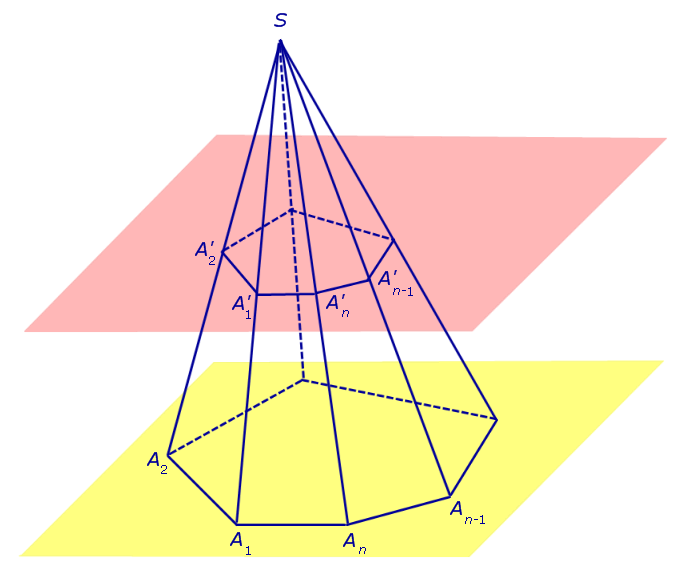
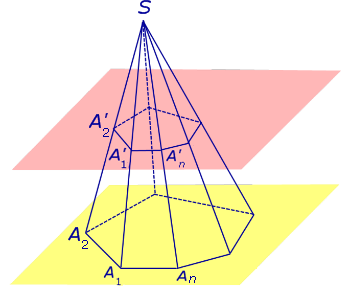
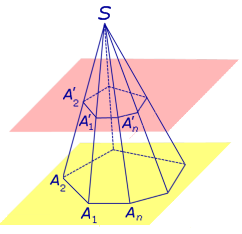
Расстояние между плоскостями Расстояние между плоскостями оснований усеченной пирамиды называют высотой усеченной пирамиды.
Множество всех боковых граней усеченной пирамиды составляет боковую поверхность усеченной пирамиды.
Полная поверхность усеченной пирамиды состоит из оснований усеченной пирамиды и ее боковой поверхности.
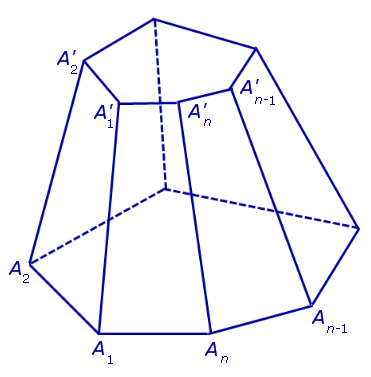
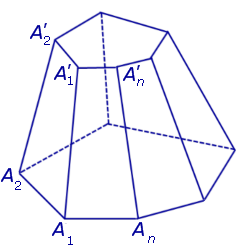
Теорема Эйлера. Для любой усеченной пирамиды справедливо равенство:
Доказательство. Заметим, что у n – угольной усеченной пирамиды 2n вершин, n боковых граней, 2 основания, 2n ребер оснований и n боковых ребер. Следовательно, у n – угольной усеченной пирамиды (n + 2) грани и 3n ребер.
то теорема Эйлера доказана.
Правильные усеченные пирамиды

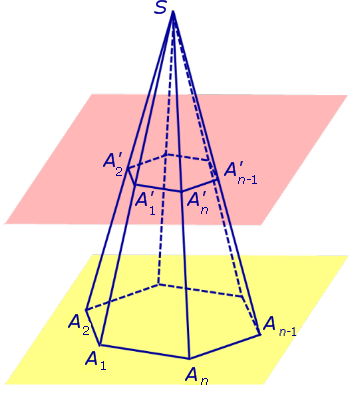
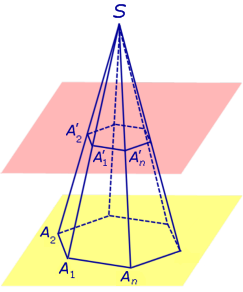
Определение 2. Высоту боковой грани правильной усеченной пирамиды называют апофемой правильной усеченной пирамиды (рис 4).
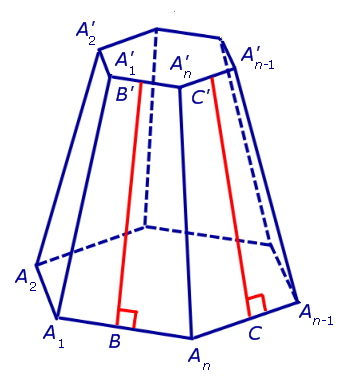
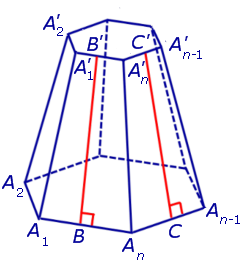
Свойства правильной усеченной пирамиды:
Все боковые ребра правильной усеченной пирамиды равны.
Все боковые грани правильной усеченной пирамиды являются равными равнобедренными трапециями.
У любой правильной усеченной пирамиды все апофемы равны.
Все боковые ребра правильной усеченной пирамиды образуют с плоскостью нижнего основания усеченной пирамиды равные углы.
Все боковые ребра правильной усеченной пирамиды образуют с плоскостью верхнего основания усеченной пирамиды равные углы.
Все боковые грани правильной усеченной пирамиды образуют с плоскостью нижнего основания усеченной пирамиды равные двугранные углы.
Все боковые грани правильной усеченной пирамиды образуют с плоскостью верхнего основания усеченной пирамиды равные двугранные углы.
Отрезок, соединяющий центры верхнего и нижнего оснований правильной усеченной пирамиды, перпендикулярен плоскостям оснований правильной усеченной пирамиды. Длина этого отрезка равна высоте правильной усеченной пирамиды.
Геометрические фигуры. Усеченная пирамида.
Усеченной пирамидой является многогранник, заключенный меж основанием пирамиды и секущей плоскостью, которая параллельна ее основанию.
Или другими словами: усеченная пирамида — это такой многогранник, который образован пирамидой и ее сечением, параллельным основанию.

Сечение, которое параллельно основанию пирамиды делит пирамиду на 2 части. Часть пирамиды меж ее основанием и сечением — это усеченная пирамида.
Это сечение для усеченной пирамиды оказывается 1-ним из оснований этой пирамиды.
Расстояние меж основаниями усеченной пирамиды является высотой усеченной пирамиды.
Усеченная пирамида будет правильной, когда пирамида, из которой она была получена, тоже была правильной.
Высота трапеции боковой грани правильной усеченной пирамиды является апофемой правильной усеченной пирамиды.
Свойства усеченной пирамиды.
1. Каждая боковая грань правильной усеченной пирамиды является равнобокими трапециями одной величины.
2. Основания усеченной пирамиды являются подобными многоугольниками.
3. Боковые ребра правильной усеченной пирамиды имеют равную величину и один наклонен по отношению к основанию пирамиды.
4. Боковые грани усеченной пирамиды являются трапециями.
5. Двугранные углы при боковых ребрах правильной усеченной пирамиды имеют равную величину.
Формулы для усеченной пирамиды.
Для произвольной пирамиды:
Объем усеченной пирамиды равен 1/3 произведения высоты h (OS) на сумму площадей верхнего основания S1 (abcde), нижнего основания усеченной пирамиды S2 (ABCDE) и средней пропорциональной между ними.

h — высота усеченной пирамиды.
Площадь боковой поверхности  равняется сумме площадей боковых граней усеченной пирамиды.
равняется сумме площадей боковых граней усеченной пирамиды.
Для правильной усеченной пирамиды:
Правильная усеченная пирамида — многогранник, который образован правильной пирамидой и ее сечением, которое параллельно основанию.

Площадь боковой поверхности правильной усеченной пирамиды равна ½ произведения суммы периметров ее оснований и апофемы.

φ — двугранный угол у основания пирамиды.

CH является высотой усеченной пирамиды, P1 и P2 — периметрами оснований, S1 и S2 — площадями оснований, Sбок — площадью боковой поверхности, Sполн — площадью полной поверхности:

Сечение пирамиды плоскостью, параллельной основанию.
Сечение пирамиды плоскостью, которое параллельно ее основанию (перпендикулярной высоте) разделяет высоту и боковые ребра пирамиды на пропорциональные отрезки.
Сечение пирамиды плоскостью, которое параллельно ее основанию (перпендикулярной высоте) – это многоугольник, который подобен основанию пирамиды, при этом коэффициент подобия этих многоугольников соответствует отношению их расстояний от вершины пирамиды.
Площади сечений, которые параллельны основанию пирамиды, относятся как квадраты их расстояний от вершины пирамиды.
Пирамида и усеченная пирамида
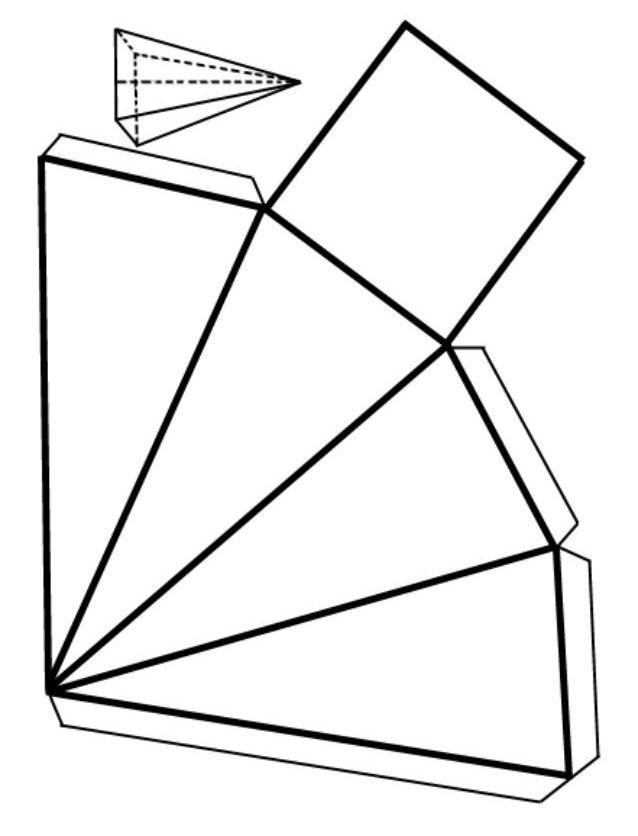
Как можно построить пирамиду? На плоскости р построим какой-либо многоугольник, например пятиугольник ABCDE. Вне плоскости р возьмем точку S. Соединив точку S отрезками со всеми точками многоугольника, получим пирамиду SABCDE (рис.).
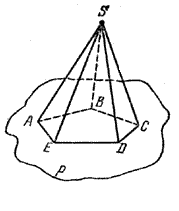
Точка S называется вершиной, а многоугольник ABCDE — основанием этой пирамиды. Таким образом, пирамида с вершиной S и основанием ABCDE — это объединение всех отрезков [SM], где М ∈ ABCDE.
Треугольники SAB, SBC, SCD, SDE, SEA называются боковыми гранями пирамиды, общие стороны боковых граней SA, SB, SC, SD, SE — боковыми ребрами.
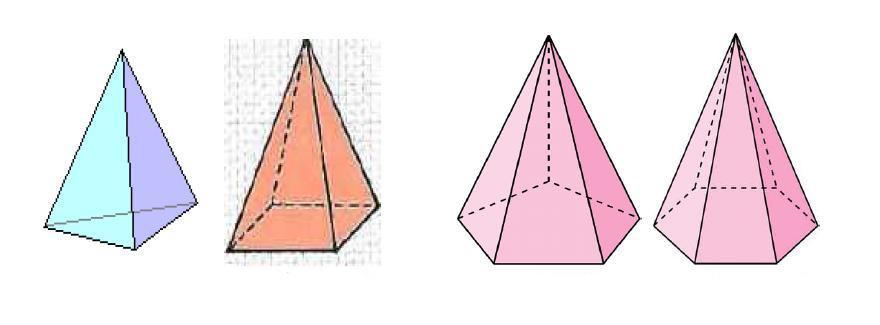
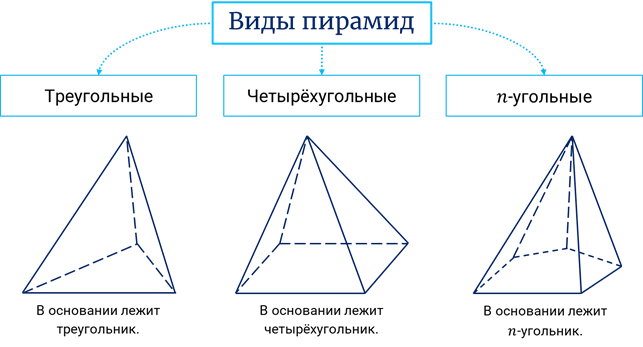
Пирамиды называются треугольными, четырехугольными, п-угольными в зависимости от числа сторон основания. На рис. даны изображения треугольной, четырехугольной и шестиугольной пирамид.
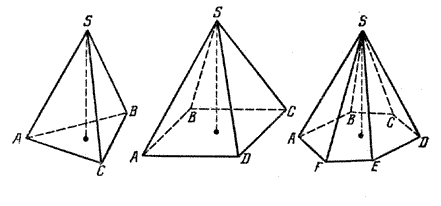
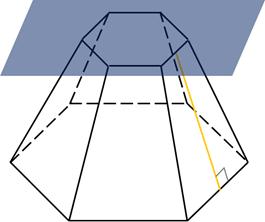
Плоскость, проходящая через вершину пирамиды и диагональ основания, называется диагональной, а полученное сечение — диагональным. На рис. 186 одно из диагональных сечений шестиугольной пирамиды заштриховано.
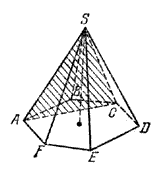
Отрезок перпендикуляра, проведенного через вершину пирамиды к плоскости ее основания, называется высотой пирамиды (концами этого отрезка являются вершина пирамиды и основание перпендикуляра).
Пирамида называется правильной, если основание пирамиды—правильный многоугольник и вершина пирамиды проектируется в его центр.
Все боковые грани правильной пирамиды — конгруэнтные равнобедренные треугольники. У правильной пирамиды все боковые ребра конгруэнтны.
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой пирамиды. Все апофемы правильной пирамиды конгруэнтны.
Если обозначить сторону основания через а, а апофему через h, то площадь одной боковой грани пирамиды равна 1 /2 ah .
Сумма площадей всех боковых граней пирамиды называется площадью боковой поверхности пирамиды и обозначается через Sбок.
Так как боковая поверхность правильной пирамиды состоит из n конгруэнтных граней, то
где Р — периметр основания пирамиды. Следовательно,
т. е. площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Площадь полной поверхности пирамиды вычисляется по формуле
Объем пирамиды равен одной трети произведения площади ее основания Socн. на высоту Н:
Вывод этой и некоторых других формул будет дан в одной из последующих глав.
Построим теперь пирамиду другим способом. Пусть дан многогранный угол, например, пятигранный, с вершиной S (рис.).
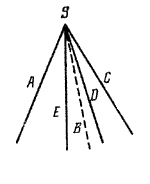
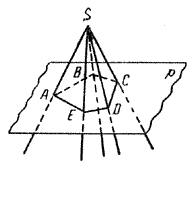
Проведем плоскость р так, чтобы она пересекала все ребра данного многогранного угла в разных точках А, В, С, D, Е (рис.). Тогда пирамиду SABCDE можно рассматривать как пересечение многогранного угла и полупространства с границей р, в котором лежит вершина S.
Очевидно, что число всех граней пирамиды может быть произвольным, но не меньшим четырех. При пересечении трехгранного угла плоскостью получается треугольная пирамида, у которой четыре грани. Любую треугольную пирамиду иногда называют тетраэдром, что означает четырехгранник.
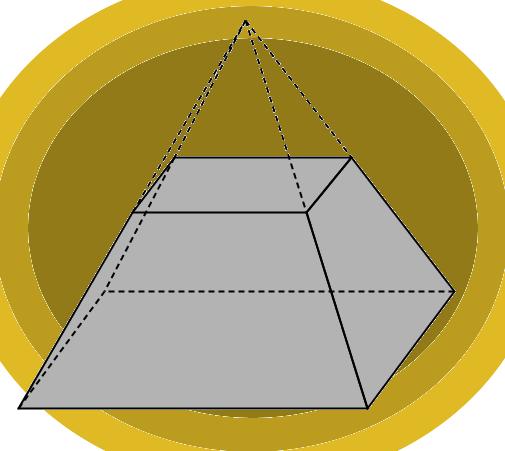
Усеченную пирамиду можно получить, если пирамиду пересечь плоскостью, параллельной плоскости основания.
На рис. дано изображение четырехугольной усеченной пирамиды.
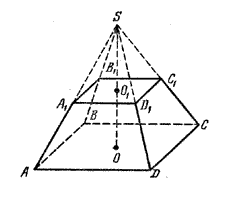
Усеченные пирамиды также называются треугольными, четырехугольными, n-угольными в зависимости от числа сторон основания. Из построения усеченной пирамиды следует, что она имеет два основания: верхнее и нижнее. Основания усеченной пирамиды — два многоугольника, стороны которых попарно параллельны. Боковые грани усеченной пирамиды — трапеции.
Высотой усеченной пирамиды называется отрезок перпендикуляра, проведенного из любой точки верхнего основания к плоскости нижнего.
Правильной усеченной пирамидой называется часть правильной пирамиды, заключенная между основанием и плоскостью сечения, параллельной основанию. Высота боковой грани правильной усеченной пирамиды (трапеции) называется апофемой.
Можно доказать, что у правильной усеченной пирамиды боковые ребра конгруэнтны, все боковые грани конгруэнтны, все апофемы конгруэнтны.
Если в правильной усеченной n-угольной пирамиде через а и bn обозначить длины сторон верхнего и нижнего оснований, а через h — длину апофемы, то площадь каждой боковой грани пирамиды равна
Сумма площадей всех боковых граней пирамиды называется площадью ее боковой поверхности и обозначается Sбок. . Очевидно, что для правильной усеченной n-угольной пирамиды
Sбок. = n • 1 /2( а + bn ) h .
Так как па = Р и nbn = Р1 — периметры оснований усеченной пирамиды, то
т. е. площадь боковой поверхности правильной усеченной пирамиды равна половине произведения суммы периметров ее оснований на апофему.
Сечение, параллельное основанию пирамиды
1) боковые ребра и высота разделятся на пропорциональные части;
2) в сечении получится многоугольник, подобный основанию;
3) площади сечения и основания относятся, как квадраты их расстояний от вершины.
Теорему достаточно доказать для треугольной пирамиды.
Так как параллельные плоскости пересекаются третьей плоскостью по параллельным прямым, то (АВ) || (А1В1), (BС) ||( В1C1), (AС) || (A1С1) (рис.).
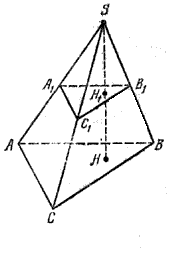
Параллельные прямые рассекают стороны угла на пропорциональные части, и поэтому
Соответственные углы треугольников ABC и A1B1C1 конгруэнтны, как углы с параллельными и одинаково направленными сторонами. Поэтому
Площади подобных треугольников относятся, как квадраты соответствующих сторон:
Теорема. Если две пирамиды с равными высотами рассечены на одинаковом расстоянии от вершины плоскостями, параллельными основаниям, то площади сечений пропорциональны площадям оснований.
Пусть (черт. 84) В и В1— площади оснований двух пирамид, H — высота каждой из них, b и b1 — площади сечений плоскостями, параллельными основаниям и удалёнными от вершин на одно и то же расстояние h.
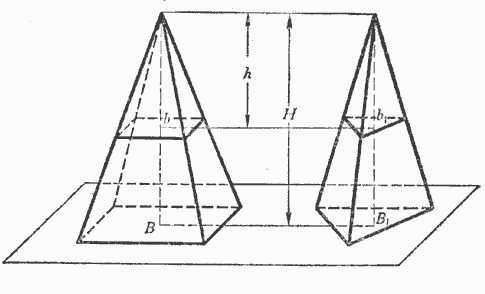
Согласно предыдущей теореме мы будем иметь:
Следствие. Если В = В1, то и b = b1 , т. е. если у двух пирамид с равными высотами основания равновелики, то равновелики и сечения, равноотстоящие от вершины.
Геометрия. 10 класс
Конспект урока
Геометрия, 10 класс
Урок № 15. Пирамида
Перечень вопросов, рассматриваемых в теме:
- Понятие пирамиды;
- Виды пирамид;
- Элементы пирамиды: вершина, ребра, грани, основание;
- Площадь боковой поверхности и полной поверхности пирамиды.
Глоссарий по теме
Пирамида – многогранник, составленный из n-угольника и n треугольников
Основание пирамиды – грань пирамиды, являющаяся n-угольником
Вершина пирамиды – общая точка всех треугольников, лежащих в боковых гранях.
Боковая грань – грань пирамиды, являющаяся треугольником
Боковые ребра – общие отрезки боковых граней
Высота – перпендикуляр, опущенный из вершины пирамиды на ее основание
Апофема – высота боковой грани правильной пирамиды
Правильная пирамида – пирамида, в основании которой лежит правильный многоугольник, а отрезок, соединяющий вершину и центр основания пирамиды, является высотой
Усеченная пирамида – многогранник, образованный двумя n-угольниками, расположенными в параллельных плоскостях (нижнее и верхнее основание) и n-четырехугольников (боковые грани).
Площадь полной поверхности пирамиды – сумма площадей всех граней пирамиды
Площадь боковой поверхности пирамиды – сумма площадей боковых граней пирамиды
Основная литература:
Потоскуев Е.В., Звавич Л. И. Геометрия. 11кл.: учеб. Для классов с углубл. и профильным изучением математики общеобразоват. Учреждений.. – М.: Дрофа, 2009. – 368 с.: ил. (117 с. – 121 с.)
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы : учеб. Для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255 с. (65 с. – 68 с.)
Открытые электронные ресурсы:
Многогранники.ru – сайт о создании моделей многогранников из бумаги https://www.mnogogranniki.ru/
Теоретический материал для самостоятельного изучения
Определение пирамиды
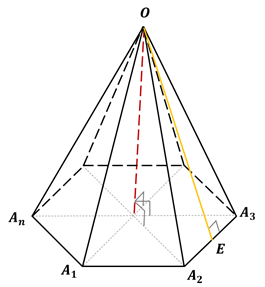
Рассмотрим многоугольник A1A2. An и точку Р, не лежащую в плоскости этого многоугольника (рис.1). Соединив точку Р с вершинами многоугольника, получим n треугольников: PA1A2, PA2A3,…, PAnA1.
Многогранник, составленный из n-угольника A1A2. An и n треугольников, называется пирамидой. Многоугольник A1A2. An называется основанием, а треугольники PA1A2, PA2A3,…, PAnA1 – боковые грани пирамиды, отрезки PA1, PA2,…, PAn – боковые ребра пирамиды, точка Р – вершина пирамиды. Пирамиду с основанием A1A2. An и вершиной Р называют n-угольной пирамидой и обозначают PA1A2. An.

Рисунок 1 – пирамида
Высота пирамиды
Перпендикуляр, проведенный из вершины пирамиды к плоскости основания, называется высотой пирамиды. На рисунке 1 PH является высотой. Обратите внимание, что высота может лежать и вне пирамиды (рис. 3) или быть одним из боковых ребер (рис. 4).

Рисунок 3 – высота вне пирамиды

Рисунок 4 – Высота пирамиды – боковое ребро
Правильная пирамида
Будем называть пирамиду правильной, если ее основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой. Напомним, что центром правильного многоугольника называется центр вписанной в него (или описанной около него) окружности (рис.5).

Рисунок 5 – Правильная пирамида
Правильная пирамида обладает несколькими хорошими свойствами. Давайте выясним, какими.
Рассмотрим правильную пирамиду PA1A2. An (рис. 5).
Пусть О – центр описанной около основания окружности, тогда РО – высота пирамиды, значит РО перпендикулярен любой прямой, лежащей в плоскости основания. Таким образом, высота РО перпендикулярна радиусам А1О, А2О. АnО.
Образованные высотой и радиусами треугольники являются прямоугольными. Причем, эти треугольники имеют общий катет – РО и равные катеты А1О, А2О. АnО (равны как радиусы). Значит, треугольники РОА1, РОА2. РОАn равны по двум катетам, значит равны гипотенузы PA1 , РA2. РAn, которые являются боковыми ребрами правильной пирамиды.
Боковые ребра пирамиды равны, значит боковые грани – равнобедренные треугольники. Основания этих треугольников равны друг другу, так как в основании лежит правильный многоугольник. Следовательно, боковые грани равны по третьему признаку равенства треугольников.
Таким образом, верны следующие утверждения:
- Все боковые ребра правильной пирамиды равны.
- Боковые ребра правильной пирамиды являются равными равнобедренными треугольниками.
Введем еще одно определение. Апофемой называется высота боковой грани правильной пирамиды, проведенная из ее вершины. На рисунке 5 PE – одна из апофем.
Все апофемы правильной пирамиды равны друг другу как высоты в равных треугольниках.
Усеченная пирамида
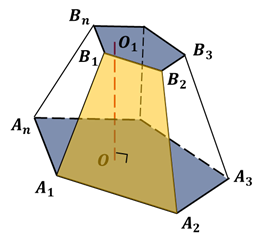
Возьмем произвольную пирамиду PA1A2. An и проведем секущую плоскость β, параллельную плоскости основания пирамиды α и пересекающую боковые ребра в точках В1,В2. Вn (рис. 6). Плоскость β разбивает пирамиду на два многогранника. Многогранник, гранями которого являются n-угольники A1A2. An и В1В2. Вn (нижнее и верхнее основания соответственно), расположенные в параллельных плоскостях и n четырехугольников A1A2B2B1, A2A3B3B2, … A1AnBnB1 (боковые грани), называется усеченной пирамидой.

Рисунок 6 – Усеченная пирамида
Отрезки A1B1, A2B2, … AnBn называют боковыми ребрами усеченной пирамиды.
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания называется высотой усеченной пирамиды. На рисунке 7 отрезки HH1 и В1O –высоты усеченной пирамиды.

Рисунок 7 – Высота усеченной пирамиды
Площадь поверхности пирамиды
Площадью полной поверхности пирамиды называются сумма площадей всех ее граней, а площадью боковой поверхности пирамиды – сумма площадей ее боковых граней.
Для пирамиды, верно равенство Sполн= Sбок+Sосн.
Докажем теорему для площади боковой поверхности правильной пирамиды.
Теорема. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Для площади боковой поверхности усеченной пирамиды верна следующая теорема
Теорема. Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему.
Примеры и разбор решения заданий тренировочного модуля
Задание 1. В пятиугольной пирамиде все боковые грани равны между собой. Площадь основания равна 42, а площадь боковой грани на 15 меньше. Чему равна площадь полной поверхности пирамиды?
Поскольку в пирамиде все боковые грани равны, то и площади их будут равны. Знаем, что площадь боковой грани на 15 меньше площади основания, значит она равна 27. В пятиугольной пирамиде боковых граней 5. Таким образом площадь полной поверхности равна 27*5+42 = 177.
Задание 2. В правильной пирамиде высота боковой грани равна 10, а в основании лежит квадрат со стороной 4. Чему равна площадь боковой поверхности?
Боковая грань пирамиды – это треугольник. Все боковые грани этой пирамиды равны между собой, так как пирамида правильная. Вычислим площадь треугольника: ½*4*10=20. В основании пирамиды лежит квадрат, значит боковых граней будет 4. Таким образом, площадь боковой поверхности равна 4* 20=80.
Площадь пирамиды определение, свойства усеченной и правильной фигуры
Пирамида – (от греч. pyramis, род. п. pyramidos), многогранник,
основание которого многоугольник, а остальные грани треугольники, имеющие
общую вершину. По числу углов основания различают пирамиды треугольные,
четырехугольные и т. д.
Общая вершина боковых граней называется вершиной пирамиды. Высотой
пирамиды называется перпендикуляр, опущенный из вершины пирамиды на
плоскость основания.
– многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину. Пирамида является частным случаем конуса .
Пирамида называется правильной, если её основанием является правильный многоугольник, а вершина проецируется в центр основани

Если все боковые ребра равны, то:
- около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр;
- боковые ребра образуют с плоскостью основания равные углы.
- также верно и обратное, то есть если боковые ребра образуют с плоскостью основания равные углы или если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.
Если боковые грани наклонены к плоскости основания под одним углом, то:
- в основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр;
- высоты боковых граней равны;
- площадь боковой поверхности равна половине произведения периметра
- Объём пирамиды может быть вычислен по формуле:
 где
где  — площадь основания и
— площадь основания и  — высота;
— высота; - Боковая поверхность — это сумма площадей боковых граней:

- Полная поверхность — это сумма площади боковой поверхности и площади основания:

- Для нахождения боковой поверхности в правильной пирамиде можно использовать формулы:
 где
где  — апофема ,
— апофема ,  — периметр основания,
— периметр основания,  — число сторон основания,
— число сторон основания,  — боковое ребро,
— боковое ребро,  — плоский угол при вершине пирамиды.
— плоский угол при вершине пирамиды.Особые случаи пирамиды
Правильная пирамида
Пирамида называется правильной, если основанием её является правильный многоугольник , а вершина проецируется в центр основания. Тогда она обладает такими свойствами:
- боковые ребра правильной пирамиды равны;
- в правильной пирамиде все боковые грани — равные равнобедренные треугольники;
- в любую правильную пирамиду можно как вписать, так и описать около неё сферу;
- если центры вписанной и описанной сферы совпадают, то сумма плоских углов при вершине пирамиды равна
 , а каждый из них соответственно
, а каждый из них соответственно  , где n — количество сторон многоугольника основания [6] ;
, где n — количество сторон многоугольника основания [6] ;
- площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Прямоугольная пирамида
Пирамида называется прямоугольной, если одно из боковых рёбер пирамиды перпендикулярно основанию. В данном случае, это ребро и является высотой пирамиды.
Усечённая пирамида
Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.
Пирамида. Площади поверхностей. Объём
Урок 36. Подготовка к ЕГЭ по математике


В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности



Конспект урока “Пирамида. Площади поверхностей. Объём”
Напомним, что пирамида – это многогранник, в основании которого лежит
 –угольник, а остальные
–угольник, а остальные  граней – треугольники с общей вершиной.
граней – треугольники с общей вершиной.Многоугольник
 называется основанием пирамиды.
называется основанием пирамиды.Треугольники
 ,
,  , …,
, …,  называются боковыми гранями пирамиды.
называются боковыми гранями пирамиды.Точка
 – вершиной пирамиды, а отрезки
– вершиной пирамиды, а отрезки  ,
,  , …,
, …,  – её боковыми рёбрами.
– её боковыми рёбрами.Отрезок, соединяющий вершину пирамиды с плоскостью её основания и перпендикулярный к этой плоскости, называется высотой пирамиды.
Пирамиду с вершиной
 и основанием
и основанием  называют
называют  -угольной пирамидой и обозначают так:
-угольной пирамидой и обозначают так:  .
.
Диагональное сечение – это сечение пирамиды плоскостью, которая проходит через два боковых ребра, не принадлежащих одной грани.

Объединение боковых граней называется боковой поверхностью пирамиды, а объединение всех граней называется полной поверхностью пирамиды.
Тогда площадью боковой поверхности пирамиды называется сумма площадей её боковых граней.

А площадью полной поверхности пирамиды называется сумма площадей всех её граней.

Объём пирамиды равен:
 .
.Пирамида, в зависимости от того, какой многоугольник лежит в основании, имеет своё название.

Пирамида называется правильной, если её основанием является правильный многоугольник, а все боковые рёбра равны.
Отрезок, соединяющий вершину пирамиды с центром основания, является её высотой.
Высота боковой грани правильной пирамиды, проведённая из её вершины к ребру основания, называется апофемой.

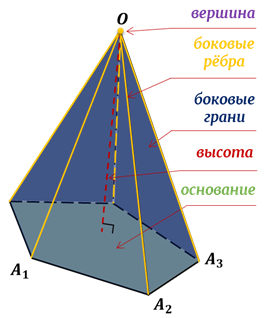
Выше изображена правильная пирамида.
 – одна из её апофем. Все апофемы правильной пирамиды равны друг другу.
– одна из её апофем. Все апофемы правильной пирамиды равны друг другу.Отметим некоторые свойства правильной
 -угольной пирамиды.
-угольной пирамиды.1. В правильной
 -угольной пирамиде все боковые рёбра равны между собой.
-угольной пирамиде все боковые рёбра равны между собой.
2. Боковые рёбра равно наклонены к основанию.
3. Из равенства боковых рёбер пирамиды следует и равенство её боковых граней.

4. Боковые грани равно наклонены к основанию.
5. Вершина проектируется в центр основания (основание высоты совпадает с центром основания).
6. Площадь боковой поверхности правильной пирамиды равна:
 .
.7. Объём правильной четырёхугольной пирамиды со стороной основания
 и высотой
и высотой  равен:
равен: .
.Параллельное сечение пирамиды – сечение пирамиды плоскостью, параллельной основанию.
Параллельное сечение пирамиды обладает следующими свойствами:
1. сечение, параллельное основанию пирамиды, отсекает на высоте пирамиды и боковых рёбрах пропорциональные отрезки;
2. в сечении получается многоугольник, подобный основанию;
3. площади сечения и основания относятся как квадраты их расстояний до вершины.

Усечённая пирамида – это часть пирамиды, заключённая между основанием и параллельным сечением пирамиды.
Основания усечённой пирамиды – подобные многоугольники, лежащие в параллельных плоскостях.
Боковые грани усечённой пирамиды – трапеции.
Высота усечённой пирамиды – это перпендикуляр, опущенный из любой точки верхнего основания на плоскость нижнего.
Площадь полной поверхности усечённой пирамиды равна сумме площади боковой поверхности и площадей двух оснований.
Объём усечённой пирамиды равен разности объёмов полной и отсечённой пирамиды, или его ещё можно вычислить по следующей формуле:
 .
.
Правильная усечённая пирамида получается из правильной пирамиды.
Апофема – высота боковой грани правильной усечённой пирамиды.
Площадь боковой поверхности правильной усечённой пирамиды равна:
 .
.
Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.
Задача первая. Дана треугольная пирамида, боковые рёбра которой взаимно перпендикулярны и равны
 см,
см,  см и
см и  см. Найдите площадь боковой поверхности пирамиды.
см. Найдите площадь боковой поверхности пирамиды.
Задача вторая. Дана правильная четырёхугольная пирамида со стороной основания
 см и высотой
см и высотой  см. Найдите площадь полной поверхности пирамиды.
см. Найдите площадь полной поверхности пирамиды.


Задача третья. Найдите высоту правильной усечённой треугольной пирамиды
 , если стороны её оснований равны
, если стороны её оснований равны  см и
см и  см, а боковое ребро равно
см, а боковое ребро равно  см.
см.

Задача четвёртая. В пирамиде
 боковое ребро
боковое ребро  перпендикулярно основанию и равно ребру
перпендикулярно основанию и равно ребру  . Треугольник
. Треугольник  – прямоугольный с катетами
– прямоугольный с катетами  см и
см и  см. Найдите объём пирамиды.
см. Найдите объём пирамиды.

Задача пятая. Найдите объём правильной треугольной пирамиды с ребром основания, равным
 см, и боковым ребром, равным
см, и боковым ребром, равным  см.
см.Формулы и свойства правильной четырехугольной пирамиды. Усеченная пирамида
Когда человек слышит слово “пирамида”, то сразу вспоминает величественные египетские сооружения. Тем не менее древние каменные гиганты являются лишь одним из представителей класса пирамид. В данной статье рассмотрим с геометрической точки зрения свойства правильной четырехугольной пирамиды .
Что такое пирамида в общем случае?
В геометрии под ней понимают объемную фигуру, получить которую можно, если соединить все вершины плоского многоугольника с одной единственной точкой, лежащей в другой плоскости, чем этот многоугольник. Рисунок ниже показывает 4 фигуры, которые удовлетворяют данному определению.
 Вам будет интересно: Литовские статуты: даты и история изданий, регламент, хронология принятия статутов
Вам будет интересно: Литовские статуты: даты и история изданий, регламент, хронология принятия статутов 
Мы видим что первая фигура имеет треугольное основание, вторая – четырехугольное. Две последние представлены пяти- и шестиугольным основанием. Однако боковая поверхность всех пирамид образована треугольниками. Их число точно равно количеству сторон или вершин многоугольника в основании.
Особым типом пирамид, которые от остальных представительниц класса отличаются идеальной симметрией, являются правильные пирамиды. Чтобы фигура была правильной, должны выполняться следующие два обязательных условия:
- в основании должен находиться правильный многоугольник;
- боковая поверхность фигуры должна состоять из равных равнобедренных треугольников.
Отметим, что второе обязательное условие можно заменить иным: перпендикуляр, проведенный к основанию из вершины пирамиды (точка пересечения боковых треугольников), должен пересекать это основание в его геометрическом центре.
Правильная четырехугольная пирамида
Теперь перейдем к теме статьи и рассмотрим, какие свойства правильной четырехугольной пирамиды характеризуют ее. Сначала покажем на рисунке, как выглядит эта фигура.

Ее основание является квадратом. Боковые стороны представляют 4 одинаковых равнобедренных треугольника (они также могут быть равносторонними при определенном соотношении длины стороны квадрата и высоты фигуры). Опущенная из вершины пирамиды высота пересечет квадрат в его центре (точка пересечения диагоналей).
Эта пирамида имеет 5 граней (квадрат и четыре треугольника), 5 вершин (четыре из них принадлежат основанию) и 8 ребер. Ось симметрии четвертого порядка, проходящая через высоту пирамиды, переводит ее в саму себя путем поворота на 90o.
Египетские пирамиды в Гизе являются правильными четырехугольными.
Далее приведем формулы, позволяющие определить все характеристики этой фигуры.
Четыре основных линейных параметра
Начнем рассмотрение математических свойств правильной четырехугольной пирамиды с формул высоты, длины стороны основания, бокового ребра и апофемы. Сразу скажем, что все эти величины связаны друг с другом, поэтому достаточно знать только две из них, чтобы однозначно вычислить оставшиеся две.
Предположим, что известна высота h пирамиды и длина a стороны квадратного основания, тогда боковое ребро b будет равно:
Теперь приведем формулу для длины ab апофемы (высота треугольника, опущенная на сторону основания):
Очевидно, что боковое ребро b всегда больше апофемы ab.
Оба выражения можно применять для определения всех четырех линейных характеристик, если известны другие два параметра, например ab и h.
Площадь и объем фигуры
Это еще два важных свойства правильной четырехугольной пирамиды . Основание фигуры имеет следующую площадь:
Эту формулу знает каждый школьник. Площадь боковой поверхности, которая образована четырьмя одинаковыми треугольниками, можно определить через апофему ab пирамиды так:
Если ab является неизвестной, то можно ее определить по формулам из предыдущего пункта через высоту h или ребро b.
Общая площадь поверхности рассматриваемой фигуры складывается из площадей So и Sb:
S = So + Sb = a2 + 2 × a × ab = a (a + 2 × ab)
Рассчитанная площадь всех граней пирамиды показана на рисунке ниже в виде ее развертки.

Описание свойств правильной четырехугольной пирамиды не будет полным, если не рассмотреть формулу для определения ее объема. Эта величина для рассматриваемой пирамиды вычисляется следующим образом:
То есть V равен третьей части произведения высоты фигуры на площадь ее основания.
Свойства правильной усеченной четырехугольной пирамиды
Получить эту фигуру можно из исходной пирамиды. Для этого необходимо срезать верхнюю часть пирамиды плоскостью. Оставшаяся под плоскостью среза фигура будет называться пирамидой усеченной.

Удобнее всего изучать характеристики усеченной пирамиды, если ее основания параллельны друг другу. В этом случае нижнее и верхнее основания будут подобными многоугольниками. Поскольку в четырехугольной правильной пирамиде основание – это квадрат, то образованное при срезе сечение тоже будет представлять квадрат, но уже меньшего размера.
Боковая поверхность усеченной фигуры образована не треугольниками, а равнобедренными трапециями.
Одним из важных свойств этой пирамиды является ее объем, который рассчитывается по формуле:
V = 1/3 × h × (So1 + So2 + √(So1 × So2))
Здесь h – расстояние между основаниями фигуры, So1, So2 – площади нижнего и верхнего оснований.
 где
где 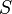 — площадь основания и
— площадь основания и 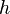 — высота;
— высота; 

 где
где  — апофема ,
— апофема ,  — периметр основания,
— периметр основания,  — число сторон основания,
— число сторон основания,  — боковое ребро,
— боковое ребро,  — плоский угол при вершине пирамиды.
— плоский угол при вершине пирамиды. , а каждый из них соответственно
, а каждый из них соответственно  , где n — количество сторон многоугольника основания [6] ;
, где n — количество сторон многоугольника основания [6] ;




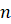 –угольник, а остальные
–угольник, а остальные 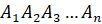 называется основанием пирамиды.
называется основанием пирамиды.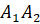 ,
, 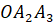 , …,
, …, 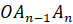 называются боковыми гранями пирамиды.
называются боковыми гранями пирамиды.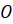 – вершиной пирамиды, а отрезки
– вершиной пирамиды, а отрезки 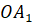 ,
, 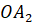 , …,
, …, 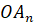 – её боковыми рёбрами.
– её боковыми рёбрами.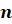 -угольной пирамидой и обозначают так:
-угольной пирамидой и обозначают так: 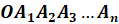 .
.

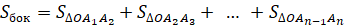
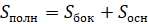
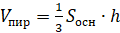 .
.
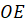 – одна из её апофем. Все апофемы правильной пирамиды равны друг другу.
– одна из её апофем. Все апофемы правильной пирамиды равны друг другу.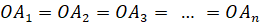
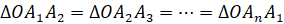
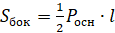 .
.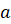 и высотой
и высотой 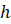 равен:
равен: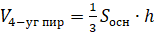 .
.
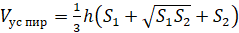 .
.
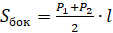 .
.
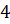 см,
см, 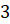 см и
см и 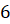 см. Найдите площадь боковой поверхности пирамиды.
см. Найдите площадь боковой поверхности пирамиды.


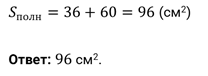
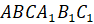 , если стороны её оснований равны
, если стороны её оснований равны 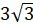 см и
см и 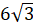 см, а боковое ребро равно
см, а боковое ребро равно 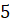 см.
см.

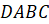 боковое ребро
боковое ребро 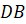 перпендикулярно основанию и равно ребру
перпендикулярно основанию и равно ребру 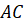 . Треугольник
. Треугольник 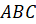 – прямоугольный с катетами
– прямоугольный с катетами 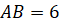 см и
см и 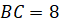 см. Найдите объём пирамиды.
см. Найдите объём пирамиды.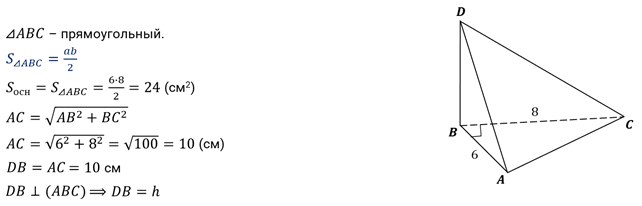
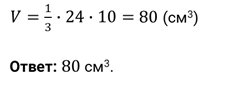
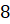 см.
см. Вам будет интересно: Литовские статуты: даты и история изданий, регламент, хронология принятия статутов
Вам будет интересно: Литовские статуты: даты и история изданий, регламент, хронология принятия статутов