Определитель матрицы: алгоритм и примеры вычисления определителя матрицы
Определитель (детерминант) матрицы — некоторое число, с которым можно сопоставить любую квадратную матрицу А = ( a i j ) n × n .
|А|, ∆ , det A – символы, которыми обозначают определитель матрицы.
Способ вычисления определителя выбирают в зависимости от порядка матрицы.
Определитель матрицы 2-го порядка вычисляют по формуле:
d e t A = 1 – 2 3 1 = 1 × 1 – 3 × ( – 2 ) = 1 + 6 = 7
Определитель матрицы 3-го порядка: правило треугольника
Чтобы найти определитель матрицы 3-го порядка, необходимо одно из правил:
- правило треугольника;
- правило Саррюса.
Как найти определитель матрицы 3-го порядка по методу треугольника?
а 11 а 12 а 13 а 21 а 22 а 23 а 31 а 32 а 33 = a 11 × a 22 × a 33 + a 31 × a 12 × a 23 + a 21 × a 32 × a 13 – a 31 × a 22 × a 13 – a 21 × a 12 × a 33 – a 11 × a 23 × a 32
А = 1 3 4 0 2 1 1 5 – 1
d e t A = 1 3 4 0 2 1 1 5 – 1 = 1 × 2 × ( – 2 ) + 1 × 3 × 1 + 4 × 0 × 5 – 1 × 2 × 4 – 0 × 3 × ( – 1 ) – 5 × 1 × 1 = ( – 2 ) + 3 + 0 – 8 – 0 – 5 = – 12
Правило Саррюса
Чтобы вычислить определитель по методу Саррюса, необходимо учесть некоторые условия и выполнить следующие действия:
- дописать слева от определителя два первых столбца;
- перемножить элементы, которые расположены на главной диагонали и параллельных ей диагоналях, взяв произведения со знаком «+»;
- перемножить элементы, которые расположены на побочных диагоналях и параллельных им, взяв произведения со знаком «—».
а 11 а 12 а 13 а 21 а 22 а 23 а 31 а 32 а 33 = a 11 × a 22 × a 33 + a 31 × a 12 × a 23 + a 21 × a 32 × a 13 – a 31 × a 22 × a 13 – a 21 × a 12 × a 33 – a 11 × a 23 × a 32
А = 1 3 4 0 2 1 – 2 5 – 1 1 3 0 2 – 2 5 = 1 × 2 × ( – 1 ) + 3 × 1 × ( – 2 ) + 4 × 0 × 5 – 4 × 2 × ( – 2 ) – 1 × 1 × 5 – 3 × 0 × ( – 1 ) = – 2 – 6 + 0 + 16 – 5 – 0 = 3
Методы разложения по элементам строки и столбца
Чтобы вычислить определитель матрицу 4-го порядка, можно воспользоваться одним из 2-х способов:
- разложением по элементам строки;
- разложением по элементам столбца.
Представленные способы определяют вычисление определителя n как вычисление определителя порядка n-1 за счет представления определителя суммой произведений элементов строки (столбца) на их алгебраические дополнения.
Разложение матрицы по элементам строки:
d e t A = a i 1 × A i 1 + a i 2 × A i 2 + . . . + а i n × А i n
Разложение матрицы по элементам столбца:
d e t A = а 1 i × А 1 i + а 2 i × А 2 i + . . . + а n i × А n i
Если раскладывать матрицу по элементам строки (столбца), необходимо выбирать строку (столбец), в которой(-ом) есть нули.
А = 0 1 – 1 3 2 1 0 0 – 2 4 5 1 3 2 1 0
- раскладываем по 2-ой строке:
А = 0 1 – 1 3 2 1 0 0 – 2 4 5 1 3 2 1 0 = 2 × ( – 1 ) 3 × 1 – 1 3 – 2 5 1 3 1 0 = – 2 × 1 – 1 3 4 5 1 2 1 0 + 1 × 0 – 1 3 – 2 5 1 3 1 0
- раскладываем по 4-му столбцу:
А = 0 1 – 1 3 2 1 0 0 – 2 4 5 1 3 2 1 0 = 3 × ( – 1 ) 5 × 2 1 0 – 2 4 5 3 2 1 + 1 × ( – 1 ) 7 × 0 1 – 1 2 1 0 3 2 1 = – 3 × 2 1 0 – 2 4 5 3 2 1 – 1 × 0 1 – 1 2 1 0 3 2 1
Свойства определителя
- если преобразовывать столбцы или строки незначительными действиями, то это не влияет на значение определителя;
- если поменять местами строки и столбцы, то знак поменяется на противоположный;
- определитель треугольной матрицы представляет собой произведение элементов, которые расположены на главной диагонали.
Пример 6
А = 1 3 4 0 2 1 0 0 5
d e t А = 1 3 4 0 2 1 0 0 5 = 1 × 5 × 2 = 10
Определитель матрицы, который содержит нулевой столбец, равняется нулю.
Методы вычисления определителей
В общем случае правило вычисления определителей $n$-го порядка является довольно громоздким. Для определителей второго и третьего порядка существуют рациональные способы их вычислений.
Вычисления определителей второго порядка
Чтобы вычислить определитель матрицы 
второго порядка, надо от произведения элементов главной диагонали отнять произведение элементов побочной диагонали:
Задание. Вычислить определитель второго порядка $left| begin
Решение. $left| begin
Методы вычисления определителей третьего порядка
Для вычисления определителей третьего порядка существует такие правила.
Правило треугольника
Схематически это правило можно изобразить следующим образом:
Произведение элементов в первом определителе, которые соединены прямыми, берется со знаком “плюс”; аналогично, для второго определителя – соответствующие произведения берутся со знаком “минус”, т.е.
Методы вычисления определителей не по зубам? Тебе ответит эксперт через 10 минут!
Задание. Вычислить определитель $left| begin
Решение. $left| begin
$$+3 cdot 3 cdot 1-(-1) cdot 1 cdot 1-3 cdot(-2) cdot 3-4 cdot 3 cdot(-2)=54$$
Правило Саррюса
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком “плюс”; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком “минус”:
Задание. Вычислить определитель $left| begin
Решение. 
$$+(-1) cdot 4 cdot(-2)-(-1) cdot 1 cdot 1-3 cdot 3 cdot(-2)-3 cdot 4 cdot(-2)=54$$
Разложение определителя по строке или столбцу
Определитель равен сумме произведений элементов строки определителя на их алгебраические дополнения. Обычно выбирают ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.
Задание. Разложив по первой строке, вычислить определитель $left| begin
Решение. $left| begin
Этот метод позволяет вычисление определителя свести к вычислению определителя более низкого порядка.
Задание. Вычислить определитель $left| begin
Решение. Выполним следующие преобразования над строками определителя: из второй строки отнимем четыре первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель, равный данному.
Определитель равен нулю, так как вторая и третья строки являются пропорциональными.
Для вычисления определителей четвертого порядка и выше применяется либо разложение по строке/столбцу, либо приведение к треугольному виду, либо с помощью теоремы Лапласа.
Разложение определителя по элементам строки или столбца
Задание. Вычислить определитель $left| begin
Решение. Предварительно выполним элементарные преобразования над строками определителя, сделав как можно больше нулей либо в строке, либо в столбце. Для этого вначале от первой строки отнимем девять третьих, от второй – пять третьих и от четвертой – три третьих строки, получаем:
Полученный определитель разложим по элементам первого столбца:
Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули, например, в первом столбце. Для этого от первой строки отнимаем две вторые строки, а от третьей – вторую:
$$=4 cdot(2 cdot 8-4 cdot 4)=0$$
Последний и предпоследний определители можно было бы и не вычислять, а сразу сделать вывод о том, что они равны нулю, так как содержат пропорциональные строки.
Приведение определителя к треугольному виду
С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его значение, согласно свойствам определителя, равно произведению элементов стоящих на главной диагонали.
Задание. Вычислить определитель $Delta=left| begin
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования будет выполнять проще, если элемент $a_<11>$ будет равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя, приведет к тому, что он сменит знак на противоположный:
Далее получим нули в первом столбце, кроме элемента $a_<11>$ , для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:
Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если диагональный элемент будет равен $pm 1$ , то вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на противоположный знак определителя):
Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом: к третьей строке прибавляем три вторых, а к четвертой – две вторых строки, получаем:
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под главной диагональю, а для этого к последней строке прибавляем третью:
Ответ. $Delta=-80$
Теорема Лапласа
Пусть $Delta$ – определитель $n$-го порядка. Выберем в нем произвольные $k$ строк (или столбцов), причем $k leq n-1$ . Тогда сумма произведений всех миноров $k$-го порядка, которые содержатся в выбранных $k$ строках (столбцах), на их алгебраические дополнения равна определителю.
Задание. Используя теорему Лапласа, вычислить определитель $left| begin
Решение. Выберем в данном определителе пятого порядка две строки – вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем):
Как вычислить определитель?
В ходе решения задач по высшей математике очень часто возникает необходимость вычислить определитель матрицы. Определитель матрицы фигурирует в линейной алгебре, аналитической геометрии, математическом анализе и других разделах высшей математики. Таким образом, без навыка решения определителей просто не обойтись. Также для самопроверки Вы можете бесплатно скачать калькулятор определителей, он сам по себе не научит решать определители, но очень удобен, поскольку всегда выгодно заранее знать правильный ответ!
Я не буду давать строгое математическое определение определителя, и, вообще, буду стараться минимизировать математическую терминологию, большинству читателей легче от этого не станет. Задача данной статьи – научить Вас решать определители второго, третьего и четвертого порядка. Весь материал изложен в простой и доступной форме, и даже полный (пустой) чайник в высшей математике после внимательного изучения материала сможет правильно решать определители.
Определитель можно вычислить только для квадратной матрицы (более подробно см. Действия с матрицами)
На практике чаще всего можно встретить определитель второго порядка, например: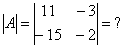 
, и определитель третьего порядка, например: 
.
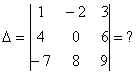Определитель четвертого порядка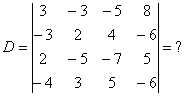 
тоже не антиквариат, и к нему мы подойдём в конце урока.
Надеюсь, всем понятно следующее: Числа внутри определителя живут сами по себе, и ни о каком вычитании речи не идет! Менять местами числа нельзя!
(Как частность, можно осуществлять парные перестановки строк или столбцов определителя со сменой его знака, но часто в этом нет никакой необходимости – см. следующий урок Свойства определителя и понижение его порядка)
Таким образом, если дан какой-либо определитель, то ничего внутри него не трогаем!
Обозначения: Если дана матрица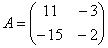 
, то ее определитель обозначают 
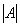. Также очень часто определитель обозначают латинской буквой 
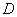или греческой 
.
1) Что значит решить (найти, раскрыть) определитель? Вычислить определитель – это значит НАЙТИ ЧИСЛО. Знаки вопроса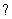 
в вышерассмотренных примерах – это совершенно обыкновенные числа.
2) Теперь осталось разобраться в том, КАК найти это число? Для этого нужно применить определенные правила, формулы и алгоритмы, о чём сейчас и пойдет речь.
Начнем с определителя «два» на «два»:
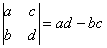
ЭТО НУЖНО ЗАПОМНИТЬ, по крайне мере на время изучения высшей математики в ВУЗе.
Сразу рассмотрим пример:
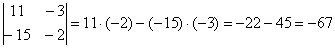
Готово. Самое главное, НЕ ЗАПУТАТЬСЯ В ЗНАКАХ.
Определитель матрицы «три на три» можно раскрыть 8 способами, 2 из них простые и 6 – нормальные.
Начнем с двух простых способов
Аналогично определителю «два на два», определитель «три на три» можно раскрыть с помощью формулы:
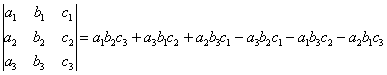
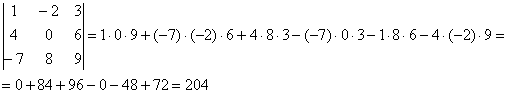
Формула длинная и допустить ошибку по невнимательности проще простого. Как избежать досадных промахов? Для этого придуман второй способ вычисления определителя, который фактически совпадает с первым. Называется он способом Саррюса или способом «параллельных полосок».
Суть состоит в том, что справа от определителя приписывают первый и второй столбец и аккуратно карандашом проводят линии:
Множители, находящиеся на «красных» диагоналях входят в формулу со знаком «плюс».
Множители, находящиеся на «синих» диагоналях входят в формулу со знаком минус:
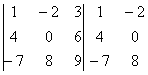
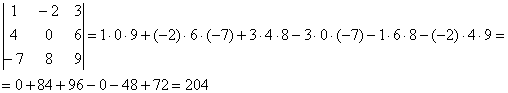
Сравните два решения. Нетрудно заметить, что это ОДНО И ТО ЖЕ, просто во втором случае немного переставлены множители формулы, и, самое главное, вероятность допустить ошибку значительно меньше.
Теперь рассмотрим шесть нормальных способов для вычисления определителя
Почему нормальных? Потому что в подавляющем большинстве случаев определители требуется раскрывать именно так.
Как Вы заметили, у определителя «три на три» три столбца и три строки.
Решить определитель можно, раскрыв его по любой строке или по любому столбцу.
Таким образом, получается 6 способов, при этом во всех случаях используется однотипный алгоритм.
Определитель матрицы равен сумме произведений элементов строки (столбца) на соответствующие алгебраические дополнения. Страшно? Все намного проще, будем использовать ненаучный, но понятный подход, доступный даже для человека, далекого от математики.
В следующем примере будем раскрывать определитель по первой строке.
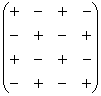
Для этого нам понадобится матрица знаков: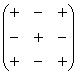 
. Легко заметить, что знаки расположены в шахматном порядке.
Внимание! Матрица знаков – это мое собственное изобретение. Данное понятие не научное, его не нужно использовать в чистовом оформлении заданий, оно лишь помогает Вам понять алгоритм вычисления определителя.
Сначала я приведу полное решение. Снова берем наш подопытный определитель и проводим вычисления:
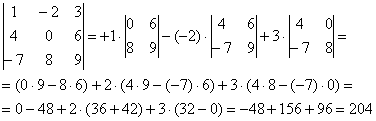
И главный вопрос: КАК из определителя «три на три» получить вот это вот: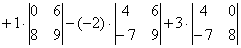 
?
Итак, определитель «три на три» сводится к решению трёх маленьких определителей, или как их еще называют, МИНОРОВ. Термин рекомендую запомнить, тем более, он запоминающийся: минор – маленький.
Коль скоро выбран способ разложения определителя по первой строке, очевидно, что всё вращается вокруг неё: 
Элементы обычно рассматривают слева направо (или сверху вниз, если был бы выбран столбец)
Поехали, сначала разбираемся с первым элементом строки, то есть с единицей:
1) Из матрицы знаков выписываем соответствующий знак: 
2) Затем записываем сам элемент: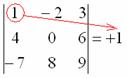 
3) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит первый элемент: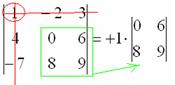 
Оставшиеся четыре числа и образуют определитель «два на два», который называется МИНОРОМ данного элемента (единицы).
Переходим ко второму элементу строки.
4) Из матрицы знаков выписываем соответствующий знак:
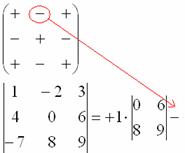
5) Затем записываем второй элемент: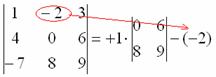 
6) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит второй элемент: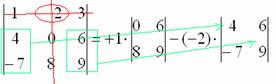 
Оставшиеся четыре числа записываем в маленький определитель.
Ну и третий элемент первой строки. Никакой оригинальности:
7) Из матрицы знаков выписываем соответствующий знак: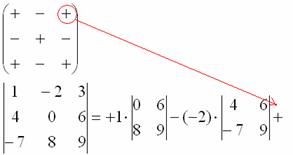 
Записываем третий элемент: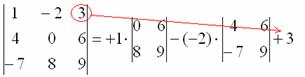 
9) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит третий элемент: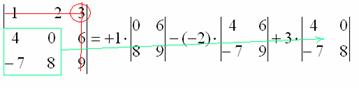 
Оставшиеся четыре числа записываем в маленький определитель.
Остальные действия не представляют трудностей, поскольку определители «два на два» мы считать уже умеем. НЕ ПУТАЕМСЯ В ЗНАКАХ!
Аналогично определитель можно разложить по любой строке или по любому столбцу. Естественно, во всех шести случаях ответ получается одинаковым.
Определитель «четыре на четыре» можно вычислить, используя этот же алгоритм.
При этом матрица знаков у нас увеличится:
В следующем примере я раскрыл определитель по четвертому столбцу:
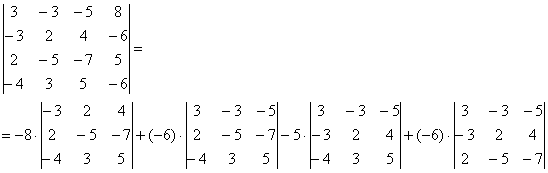
А как это получилось, попробуйте разобраться самостоятельно. Дополнительная информация будет позже. Если кто захочет прорешать определитель до конца, правильный ответ: 18. Для тренировки лучше раскрыть определитель по какому-нибудь другому столбцу или другой строке.
Потренироваться, раскрыть, провести расчёты – это очень хорошо и полезно. Но сколько времени вы потратите на большой определитель? Нельзя ли как-нибудь быстрее и надёжнее? Предлагаю ознакомиться с эффективными методами вычисления определителей на втором уроке – Свойства определителя. Понижение порядка определителя.
Автор: Емелин Александр
(Переход на главную страницу)
«Всё сдал!» — онлайн-сервис помощи студентам
Определитель матрицы свойства, методы и способы вычисления, разложение определителя по элементам строки или столбца, определитель матрицы методом Гаусса
В линейной алгебре важным понятием является определитель матрицы. Он используется для записи систем уравнений. Практически это таблица, заполненная числами. Так как математика строится на грамотной и последовательной системе определений, то для успешного решения задач нужно не только знать определители, но и разбираться в их характеристиках.
Понятие и термины
Кроме математики, матрицы нашли широкое применение в физике и других прикладных науках. Используются они и в программировании, где их называют массивами. Большинство экономических моделей также описывается достаточно простой и компактной матричной формой.
Матрица состоит из столбцов (n) и строк (m). Характеризуется она порядком и размерностью. Обычно говорят, что некий массив В имеет размер m на n. Записывают это как В =
Строки и столбцы начинают нумеровать сверху и с левой стороны. Если элементы массива равны нулю, то матрицу называют нулевой. Существует понятие главной диагонали. Располагается она сверху вниз слева. Расположенные на ней элементы называют диагональными. Когда они равны одному, а все остальные члены нулю, массив считается единичным.
Главной характеристикой массива является определитель, или детерминант. Им называют число, соответствующее алгебраической сумме всех возможных произведений столбцов на строки. Другими словами, чтобы найти значение детерминанта, нужно сумму элементов матрицы n умножить на её размерность m. При перемножении знак произведения определяется по числу инверсий. Их чётное количество соответствует положительному знаку, а нечётное – отрицательному.
Определитель — это число, которое определяет степень матрицы. Характеризуется он порядком. Так, определителем первого порядка называют значение, определяемое единственным элементом массива. Записывают его в виде выражения: A = , detA = |A| = a.
С матрицами можно выполнять любые арифметические действия и даже возводить в степень. Определитель вычисляется только в квадратной матрице, то есть в той, у которой число строк равно числу столбцов. Расчёт проводится с использованием специальных операций. Нахождение определителя построено на использовании ряда аксиом, дающих возможность вычислить характеристику матрицы любого порядка.
Параметры определителя
Использование свойств определителей даёт возможность сделать процедуру их вычисления проще. Если взять множество натуральных чисел, записанных в порядке возрастания, K = <1, 2, 3, 4, …, n>, то с ними можно выполнить две операции: перестановку и транспозицию.
Под первой понимается упорядочение множеству чисел другой последовательности. Например, <1, 2, 3, 4>— <1, 4, 3, 2>. То есть <1, 2, 3, 4, …, n>—
Для того чтобы понять, как находить детерминант матрицы, следует понять способы решения простых матриц 2х2 и 3х3. Умея находить их параметр, несложно будет определить детерминант и массив более высокого порядка. В математике матрицу принято записывать в круглых скобках, а определитель в прямых. Обозначают детерминант в формулах как det.
Если дана матрица второго порядка, то есть 2х2, то её определитель ищут по формуле: det = ab – dc, где: а и d – элементы первой строки, b и c – члены второй строки. То есть определитель находят как разность произведений диагональных элементов между собой. Например, пусть задана матрица:
Её параметр будет равняться: det = 13 * 11 – 9 * 1 = 143 – 9 = 134.
Пусть дана некая матрица три на три:
Необходимо найти её определитель. Для массива 3х3 детерминант можно найти двумя способами:
- правилом Саррюса (треугольника);
- универсальным методом.
Схематично первый способ можно представить следующим образом:
Для нахождения детерминанта по правилу треугольника нужно перемножить элементы массива, соединённые красными линиями, а затем их сложить. То же самое необходимо сделать с элементами, через которые проходит синяя линия. Затем из первого полученного значения вычесть второе. Вычитаемое и уменьшаемое состоит из трёх слагаемых. Определяются они двумя треугольниками и сумой элементов, стоящих на главной диагонали (сплошная линия).
Определитель будет равным: det = (1* (-1) * 5) + (5 * 2 * 1) + (2 * (-1) * (-2)) – (-2 * (-1) * (-1)) – (2 * 5 * 5) – (1 * 2 * (-1)) = — 5 + 10 + 4 – 2 – 20 + 2 = -11.
Второй способ проще. В его основе лежит метод разложения дискриминанта по первой строке или столбцу. То есть определитель можно найти по следующей формуле: det = a * n1 + b * n2 + c * n3, где: n1 — матрица 2х2, образованная с верхней левой части массива; n2 – матрица, полученная из второго и третьего члена первого столбца и третьего; n3 – массив, образованный из второго и третьего элемента первого столбца и третьего; a, b, c – элементы первой строчки.
Детерминант четвёртого порядка
Более сложной матрицей считается квадрат размером 4х4. Для подсчёта определителя нужно использовать универсальный способ нахождения детерминанта массива 3х3. То есть понадобится раскрыть первую строку и найти минор. Первый элемент в строке умножают на матрицу, образованную квадратом, начинающегося со второго члена следующего от него столбца.
Затем вычитают произведение второго элемента на алгебраическое дополнение, полученное путём вычёркивания первой строки и второго столбца. Далее, прибавляют третий элемент в первой строке и умножают на дополнение этого элемента. На последнем этапе вычитают четвёртый элемент верхней строки, умноженный на соответствующую ему дополнительную матрицу.
Теперь находят дискриминанты полученных матриц 3х3. Важно помнить, что знаки, стоящие перед алгебраическим дополнением, меняются. Если первый член имеет плюс, то перед вторым элементом ставится минус, перед третьим снова плюс и так далее.
Таким образом, массивы с высокими порядковыми номерами решаются методом понижения основного выражения. Если всё будет выполнено правильно, в ответе получится дискриминант, равный -13.
Например, для поиска определителя квадрата 6х6, нужно будет предварительно разложить систему по первой строке на массив низшего порядка 5х5, найти определитель матрицы 4х4, 3х3 и 2х2. Делая всё последовательно блочным методом, допустить ошибку практически невозможно. Если необходимо найти детерминант массивов десятого порядка и выше, то целесообразно находить определитель матрицы на онлайн-калькуляторе.
Стоит напомнить, что детерминант можно найти только для квадратного выражения в прямоугольной матрице. Правило нахождения определителя n порядка было предложено Лапласом. Он доказал и сформулировал теорему, гласящую о том, что величина определителей высшего порядка находится как сумма произведений частей какой-либо строки или столбца на принадлежащее им алгебраическое дополнение.
То есть выполняется разложение определителя по n строке или m столбцу.
Метод Гаусса
Способ Гаусса используется для решения системы уравнений. На их базе составляется массив. Первые столбцы образуют из коэффициентов, стоящих после неизвестных, а последний из значений, расположенных после знака равно. Для нахождения определителя этим способом необходимо выполнить два шага:
Например, необходимо найти детерминант системы уравнений:
n1 + 2 * n2 – 3 * n3 = — 4.
2*n1 + 5 * n2 – 4 * n3 = 0.
-3*n1 + n2 – 3 * n3 = 5.
На первом этапе составляют матрицу и решают её. Выделяют первую строку и пытаются обнулить все первые коэффициенты. Для этого каждый элемент нужно умножить на такое число, чтобы последующий элемент обнулился. Затем берут другую строку и обнуляют уже вторые элементы. Так, для заданной системы уравнений первую строку необходимо умножить на -2, а затем сложить со второй строкой. То есть первый элемент в первом столбце будет равен: x11 = -2 * 1 + 2 = 0; второй: x22 = -2 * 2 +5 = 1; третий: x33 = -2*(-3) – 4 = 2; четвёртый: x44 = -2* (-4) + 0 = 8.
Аналогичные действия проводят по отношению к элементам третьей строки. Для обнуления первую строчку умножают уже не на -2, а на тройку. В результате первый столбец будет состоять из двух нулевых элементов. Затем переходят к обнулению элементов во втором столбце. Делают это последовательным умножением третьей строки на – 7. В итоге получится массив с тремя нулевыми членами.
Опираясь на полученную матрицу, составляют новую систему уравнений:
n1 + 2 * n2 – 3 * n3 = -4.
Затем из последнего равенства находят n3. Полученное значение подставляют во второе уравнение и определяют n2. На последнем этапе, используя найденные величины, вычисляют n1. Для нахождения детерминанта определяют тип матрицы, в этом случае она нижнетреугольная, и вычисляют его значение det = (1 * 1 * (-20)) = -20.
Найти детерминант небольшого ранга несложно. Но существуют задания, для решения которых нужно не только проявить внимание, но и потратить много времени. Для таких случаев существуют калькуляторы, помогающие выполнить вычисление определителя матрицы онлайн.
Кроме быстрого определения ответа, они также показывают подробное решение поставленной задачи. Если же доступа к интернету нет, то можно выполнить расчёт и в excel. Делается это с помощью функции «=МОПРЕД».
Методы вычисления определителей
При вычислении определителей высокого порядка (больше 3-го) определение, как правило, не используется, так как это приводит к громоздким выражениям и требует большого количества арифметических операций. Гораздо эффективнее использовать свойства определителей . Наиболее важными для вычисления определителей являются свойства 3, 6, 9. Эти свойства можно назвать элементарными преобразованиями определителя , что соответствует элементарным преобразованиям матрицы.
I. Перестановка двух столбцов (строк) определителя приводит к изменению его знака на противоположный.
II. Умножение всех элементов одного столбца (строки) определителя на одно и то же число, отличное от нуля, приводит к умножению определителя на это число.
III. Прибавление к элементам одного столбца (строки) определителя соответствующих элементов другого столбца, умноженных на одно и то же число, не изменяет определитель.
При помощи элементарных преобразований можно упростить определитель, т.е. привести его к виду, удобному для вычислений.
Метод приведения определителя к треугольному виду
При помощи элементарных преобразований любую матрицу можно привести к верхнему (или нижнему) треугольному виду (метод Гаусса). Отсюда следует, что любой определитель, используя перечисленные выше элементарные преобразования, можно привести к треугольному виду, а затем вычислить согласно п.3 замечаний 2.2.
Итак, метод состоит из двух шагов.
1. При помощи элементарных преобразований привести определитель к треугольному виду.
2. Вычислить определитель треугольного вида, перемножая его элементы, стоящие на главной диагонали.
Пример 2.12. Вычислить определитель четвёртого порядка
Решение. 1. При помощи элементарных преобразований приведем матрицу к треугольному виду. Взяв элемент первой строки в качестве ведущего, все остальные элементы первого столбца сделаем равными нулю. Для этого ко второй строке прибавим первую, умноженную на (-2), к третьей строке прибавим первую, умноженную на (-3), а к четвертой строке прибавим первую, умноженную на (-4):
Заметим, что при использовании этих элементарных преобразований III типа определитель не изменяется.
Умножим элементы второй строки на (-1), а элементы третьей строки — на 0,5, при этом, чтобы не нарушить равенство, надо полученный определитель разделить на , т.е. умножить на (-2):
В полученной матрице нужно сделать равными нулю элементы и второго столбца, стоящие ниже главной диагонали. Для этого берем в качестве ведущего элемента и прибавляем к третьей и четвертой строкам вторую строку, умноженную на 1 и на 7 соответственно:
Осталось сделать равным нулю элемент . К четвертой строке прибавим третью, умноженную на 2 (определитель при этом не изменится):
Получили определитель треугольного вида.
2. Вычислим определитель верхней треугольной матрицы, перемножая элементы, стоящие на главной диагонали :
Метод понижения порядка определителя
Этот метод также основан на элементарных преобразованиях определителя.
1. При помощи элементарного преобразования III типа нужно в одном столбце (или одной строке) сделать равными нулю все элементы, за исключением одного.
2. Разложить определитель по этому столбцу (строке) и получить определитель меньшего порядка, чем исходный. Если его порядок больше 1, то следует перейти к п. 1, иначе вычисления закончить.
Пример 2.13. Вычислить определитель четвёртого порядка методом понижения порядка.
Решение. 1. В качестве ведущего элемента возьмем , а все остальные элементы второй строки при помощи элементарных преобразований сделаем равными нулю. Для этого ко второму столбцу прибавим четвертый, умноженный на (-3):
2. Разложим определитель по второй строке
Получили определитель третьего порядка.
Вынесем за знак определителя множитель (2) из второго столбца (точнее все элементы второго столбца умножим на 0,5 , а получившийся определитель умножим на 2):
Прибавим ко второму столбцу первый
Полученный определитель разложим по второму столбцу
Получили определитель 2-го порядка.
Прибавим ко второй строке первую, умноженную на (-2)
Разложим определитель по второй строке и заменим определитель первого порядка единственным его элементом
Результат совпадает с полученным в примере 2.7.
Метод изменения всех элементов определителя
При вычислении определителей бывает полезно изменить все его элементы, умножив их на одно и то же число, не равное нулю, либо прибавить к каждому элементу одно и то же число. Найдем формулы изменения определителя при этих преобразованиях.
Пусть дана квадратная матрица n-го порядка. Из свойства 6 следует, что при умножении всех элементов определителя n-го порядка на число определитель умножается на число .
Рассмотрим теперь определитель матрицы , элементы которой получены из соответствующих элементов матрицы прибавлением числа
Применяя свойство 7 к первому столбцу этого определителя, получаем сумму определителей
То же свойство применяем к каждому определителю (“раскладывая” второй столбец) и т.д. В итоге получим сумму определителей n-го порядка, причем определители, имеющие по два и более столбцов из элементов, равных , равны нулю (по свойству 4). Поэтому в сумме остаются только слагаемых: определитель матрицы и определителей вида
отличающихся от определителя матрицы только j-м столбцом. Раскладывая этот определитель по j-му столбцу, получаем сумму алгебраических дополнений элементов этого столбца, умноженную на
Следовательно, сумма всех таких определителей равна сумме алгебраических дополнений всех элементов матрицы , умноженной на
Окончательно получаем, что при увеличении всех элементов определителя на число , определитель увеличивается на сумму всех алгебраических дополнений, умноженную на число
Пример 2.14. Вычислить определитель n-го порядка
Решение. Рассмотрим определитель диагональной матрицы
Искомый определитель получается прибавлением к каждому элементу определителя матрицы числа . Поэтому
Определитель диагональной матрицы равен произведению диагональных элементов:
Осталось вычислить сумму алгебраических дополнений всех элементов матрицы . Заметим, что алгебраическое дополнение недиагонального элемента равно нулю ( при , так как дополнительный минор содержит нулевой столбец). Дополнительный минор диагонального элемента — это определитель диагональной матрицы, т.е.
Вычисление определителей с помощью рекуррентных уравнений
Этот метод заключается в том, что исходный определитель n-го порядка выражается через определители того же вида, но меньшего порядка. Получается рекуррентное уравнение
Решая это уравнение, находим формулу, выражающую определитель через определители и порядок
В последнюю формулу подставляем определители невысокого порядка, которые нетрудно вычислить каким-либо другим способом.
Замечание 2.6. Рекуррентным уравнением называется равенство вида , выражающее n-й член искомой числовой последовательности через её предыдущих членов . Методы решения таких уравнений рассматриваются в разд.
Пример 2.15. Вычислить определитель n-го порядка
Решение. Разложим определитель по первой строке
Первый из полученных определителей (n-l)-ro порядка обозначим , так как он имеет такой же вид, что и . Разложив последний определитель по первому столбцу, получим определитель того же вида, что и , но (n-2)-го порядка
Следовательно, искомый определитель удовлетворяет рекуррентному уравнению
Решение этого уравнения будем искать в виде , где и — неизвестные коэффициенты. Заметим, что эта формула дает решение рекуррентного уравнения при любых коэффициентах и . В самом деле, подставляя в уравнение, получаем тождество
Подберем теперь коэффициенты и в формуле так, чтобы при и она давала правильные результаты, т.е.
Решая систему уравнений получаем . Следовательно, искомый определитель равен
Пример 2.16. Вычислить определитель Вандермонда
Решение. Рассмотрим определитель
который отличается от определителя Вандермонда последним столбцом, но совпадает с ним при . Раскладывая определитель по последнему столбцу, получаем многочлен (n-1)-й степени действительной переменной
где старший коэффициент равен алгебраическому дополнению элемента
т.е. определителю — определителю Вандермонда (n-l)-ro порядка. Заметим, что при определитель равен нулю, так как он имеет два одинаковых столбца (свойство 4). Следовательно, — корень многочлена . То же самое можно сказать про числа . Все они являются корнями многочлена . Следовательно, этот многочлен имеет вид:
Подставляя в это равенство и учитывая, что , получаем рекуррентное уравнение
Записывая аналогичным образом и учитывая, что , получаем
Таким образом, определитель Вандермонда равен произведению всех разностей при .
Основные свойства определителей. Методы вычисления определителей
Определители
Понятие определителя
Любой квадратной матрице n-го порядка 
можно поставить в соответствие число, которое называется определителем (детерминантом) матрицы A и обозначается так: 
, или 
, или det A.
Определителем матрицы первого порядка 
, или определителем первого порядка, называется элемент 
Определитель второго порядка (определитель матрицы второго порядка) вычисляется следующим образом:
 |
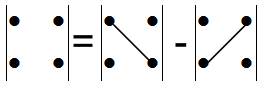Рис. Схема вычисления определителя второго порядка
Таким образом, определитель второго порядка есть сумма 2=2! слагаемых, каждое из которых представляет собой произведение 2-х сомножителей – элементов матрицы A, по одному из каждой строки и каждого столбца. Одно из слагаемых берется со знаком «+», другое – со знаком «-».
Найти определитель 
Определитель третьего порядка (определитель квадратной матрицы третьего порядка) задается равенством:
.
Таким образом, определитель третьего порядка есть сумма 6=3! слагаемых, каждое из которых представляет собой произведение 3-х сомножителей – элементов матрицы A, по одному из каждой строки и каждого столбца. Одна половина слагаемых берется со знаком «+», другая – со знаком «-».
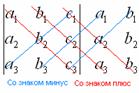
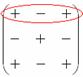
Основным методом вычисления определителя третьего порядка является так называемое правило «треугольников» (правило Саррюса): первое из трех слагаемых, входящих в сумму со знаком «+», есть произведение элементов главной диагонали, второе и третье – произведения элементов, находящихся в вершинах двух треугольников с основаниями, параллельными главной диагонали; три слагаемых, входящих в сумму со знаком «-», определяются аналогично, но относительно второй (побочной) диагонали. Ниже представлены 2 схемы вычисления определителей третьего порядка
б)
Рис. Схемы вычисления определителей 3 порядка
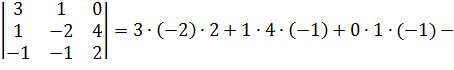
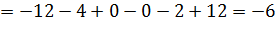
Определитель квадратной матрицы n-го порядка (n 
4) вычисляется с использованием свойств определителей.
Основные свойства определителей. Методы вычисления определителей
Определители матриц имеют следующие основные свойства:
1. Определитель не меняется при транспонировании матрицы.
2. Если в определителе поменять местами две строки (или столбца), то определитель поменяет знак.
3. Определитель с двумя пропорциональными (в частности, равными) строками (столбцами) равен нулю.
4. Если в определителе строка (столбец) состоит из нулей, то определитель равен нулю.
5. Общий множитель у элементов какой-либо строки (или столбца) можно вынести за знак определителя.
6. Определитель не изменится, если ко всем элементам одной строки (или столбца) прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и то же число.
7. Определитель диагональной и треугольной (верхней и нижней) матриц равен произведению диагональных элементов.
8. Определитель произведения квадратных матриц равен произведению их определителей.
Определитель матрицы.
Определитель матрицы (детерминант матрицы) – это квадратная таблица чисел либо математических символов (Δd).
Определение. Определителем матрицы n×n является число:
где (α1, α2. αn) – перестановка чисел от 1 до n, N (α1,α2. αn) – число инверсий в перестановке, суммирование происходит по всем вероятным перестановкам порядка n.
Определитель матрицы A в основном обозначают как de t(A), |A|, либо ?(A).
Свойства определителя матрицы.
Свойства определителя матрицы – параметры, при помощи которых находится решение всех видов алгебраических матриц.
- Определитель единичной матрицы равняется соответственно единице: det (E) = 1.
- Определитель матрицы, где две строки (столбца) равны между собой, будет равен нулю.
- Определитель матрицы, где две строки (столбца) пропорциональны друг другу также будет равен нулю.
- Определитель матрицы, который содержит строку (столбец) с одними нулями, равен нулю.
- Определитель матрицы с двумя или более строками (столбцами) линейно зависимыми между собой тоже равен только нулю.
- Если произвести транспонирование, значение определителя матрицы от этого не изменится: det (A) = det (A T )
- Определитель обратной матрицы: det (A -1 ) = det (A) -1
- Определитель матрицы будет неизменен даже если к любой его строке (столбцу) дописать другую строку (столбец), перед этим умноженную на любое число.
- Определитель матрицы не будет изменен, если к любой строке (столбцу) дописать линейную комбинацию других строк (столбцов).
- При перемене местами двух строк (столбцов) матрицы определитель матрицы получает противоположный знак.
- Общий множитель в строке (столбце) легко выносится за знак определителя:
- Умножив квадратную матрицуn-того порядка на любое число не равное нулю, то определитель итоговой матрицы будет равен произведению определителя изначально заданной матрицы на это число в степени n: B = k · A => det (B) = k n · det (A), где A матрица n×n, k – число.
- При условии, что каждый элемент любой строки определителя равняется сумме 2х слагаемых, исходный определитель равняется сумме 2х определителей, где вместо этой строки подставлены первые и вторые слагаемые соответственно, а остальные строки совпадают с начальным определителем:
- Определитель верхней (нижней) треугольной матрицы соответствует произведению его диагональных элементов.
- Определитель произведения матриц будет соответствовать произведению определителей этих матриц: det (A·B) = det (A) · det (B).
Найти определитель матрицы.
Чтобы найти определитель матрицы необходимо знать основные свойства матриц и последовательность действий при решении матрицы.
- Для матриц порядка n=2 определитель находят при помощи формулы: Δ=a11*a22–a12*a21
- Для матриц порядка n=3 определитель находят через алгебраические дополнения либо при помощи метода Саррюса.
- Матрица с размерностью >3 раскладывается на алгебраические дополнения, для которых находятся свои определители (миноры). К примеру, определитель матрицы 4 порядка вычисляется через разложение по строкам либо столбцам.
Для нахождения определителя матрицы, который содержит в матрице функции, используются стандартные методы. К примеру, найти определитель матрицы третьего порядка:
Воспользуемся разложением по первой строке:
Δ = sin(x) × [cos(x) × 2 – 0 × tg(x)] + 1×[1 × 0-2 × cos(x)] = 2sin(x) cos(x) – 2cos(x) = sin(2x) – 2cos(x)
Вычислить определитель матрицы.
Вычислить определитель матрицы можно несколькими методами, которые будут перечислены ниже.
Самым популярным способом вычисления определителя матрицы является метод подбора алгебраических дополнений. Есть более простая версия этого метода – вычисление определителя при помощи правила Саррюса. Эти методы отличны при вычислении определителя простой небольшой матрицы, а если нужно посчитать матрицу большой размерности, тогда могут применяться такие методы вычисления определителя матрицы:
- вычисление определителя методом понижения порядка,
- вычисление определителя методом Гаусса (через приведение матрицы к треугольному виду),
- вычисление определителя методом декомпозиции.
В Excel для расчета определителя используется функция =МОПРЕД (диапазон ячеек).
