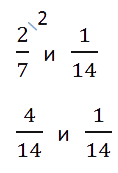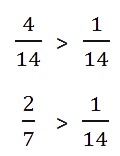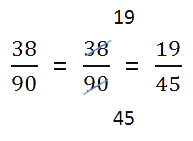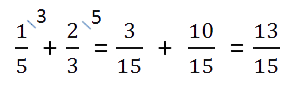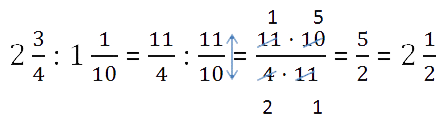Обыкновенные дроби – основное свойство, примеры, действия

ОБЫКНОВЕННАЯ ДРОБЬ

Ключевые слова конспекта: дроби, обыкновенная дробь, правильные и неправильные дроби, основное свойство дроби, сравнение дробей, арифметические действия с дробями, нахождение части от целого и целого по его части.

Одна или несколько равных частей единицы называются обыкновенной дробью. Дробь 3/4 означает, что единицу разделили на 4 части и взяли 3 таких части.

Дробь можно рассматривать и как результат деления натуральных чисел. Частное от деления натуральных чисел а и b можно записать в виде дроби a/b — где делимое а — числитель, а делитель b — знаменатель.

Правильная и неправильная дробь

Дробь, в которой числитель меньше знаменателя, называется правильной, а дробь, где числитель больше или равен знаменателю, — неправильной.

Число, состоящее из целой и дробной частей, можно обратить в неправильную дробь. Для этого нужно умножить целую часть на знаменатель и к произведению прибавить числитель данной дроби. Полученная сумма будет числителем дроби, а знаменателем остается знаменатель дробной части.

Из любой неправильной дроби можно выделить целую часть. Для этого нужно разделить с остатком числитель на знаменатель. Частное от деления — это целая часть, остаток — это числитель, делитель — это знаменатель.

Основное свойство дроби

Определение. Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной.

Основное свойство дроби используют при сокращении дробей. Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дробей.

Сравнение дробей

1. Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
2. Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.

Чтобы сравнить дроби с разными числителями и знаменателями, нужно:

• привести дроби к наименьшему общему знаменателю;
• сравнить полученные дроби.

Чтобы привести дроби к наименьшему общему знаменателю, нужно:

1. найти наименьшее общее кратное (НОК) знаменателей дробей (оно и будет их общим знаменателем);
2. разделить общий знаменатель на знаменатель данных дробей, т. е. найти для каждой дроби дополнительный множитель;
3. умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.

Арифметические действия с обыкновенными дробями

Сложение и вычитание дробей

При сложении (вычитании) дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель. Полученную дробь, если возможно, сокращают и выделяют целую часть.

При сложении (вычитании) дробей с разными знаменателями нужно предварительно привести эти дроби к наименьшему общему знаменателю, затем сложить (вычесть) полученные дроби, используя правило сложения (вычитания) дробей с одинаковыми знаменателями.

Особенно надо быть внимательным при сложении (вычитании) с участием смешанных чисел!

Общий случай сложения (вычитания) дробей.

Умножение дробей

1. Произведение двух дробей a/b и c/d равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:
   
2. При умножении чисел, состоящих из целой и дробной частей, их предварительно представляют в виде неправильных дробей, а затем умножают согласно п. 1.

Деление дробей

Два числа называются взаимно обратными, если их произведение равно 1, то есть дроби вида a/b и b/a являются взаимно обратными. Например 1/3 и 3. Чтобы разделить одну дробь на другую, нужно делимое умножить на число, обратное к делителю.

При делении чисел, состоящих из целой и дробной части, нужно предварительно представить их в виде неправильной дроби.

Нахождение части от целого (дроби от числа)

Чтобы найти часть от целого, нужно число, соответствующее целому, разделить на знаменатель дроби, выражающей эту часть, и результат умножить на числитель той же дроби.

Задача нахождения части от целого по существу является задачей нахождения дроби от числа. Чтобы найти дробь (часть) от числа, необходимо число умножить на эту дробь.

Нахождение целого по его части (числа по его дроби)

Чтобы найти целое по его части, нужно число, соответствующее этой части, разделить на числитель дроби, выражающей эту часть, и результат умножить на знаменатель той же дроби.

Задача нахождения целого по его части по существу является задачей нахождения числа по его дроби. Чтобы найти число по его дроби, необходимо данное значение разделить на эту дробь.

Это конспект по теме «Обыкновенная дробь». Выберите дальнейшие действия:

• Перейти к следующему конспекту: Десятичная дробь
• Вернуться к списку конспектов по Математике.
• Проверить знания по Математике.

Обыкновенные дроби

О чем эта статья:

Доля целого

Доля — это каждая равная часть, из суммы которых состоит целый предмет.

Для примера возьмем два мандарина. Когда мы их почистим, то получим в каждом мандарине разное количество долек или долей. В одном может быть 6, а в другом — целых 9. Размеры долей у каждого мандарина тоже разные.

У каждой доли есть свое название: оно зависит от количества долей в конкретном предмете. Если в мандарите шесть долей — каждая из них будет определяться, как одна шестая от целого.

• Половина — одна вторая доля предмета или 1/2.
• Треть — одна третья доля предмета или 1/3.
• Четверть — одна четвертая доля предмета или 1/4.

Понятие доли можно применить не только к предметам, но и величинам. Так, например, картина занимает четверть стены — при этом ее ширина треть метра.

Чтобы быстрее запомнить соотношения частей и целого, можно использовать наглядную табличку:

Понятие дроби

Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:

• обыкновенный вид — 1/2 или a/b,
• десятичный вид — 0,5.

Виды дробей:

1. Числовые — состоят из чисел. Например, 2/7 или (1,8 – 0,3)/5.
2. Алгебраические — состоят из переменных. Например, (x + y)/(x – y). Значение дроби зависит от данных значений букв.

Какие еще бывают дроби:

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.

Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 35.

Выделение целой части из неправильной дроби — это запись неправильной дроби в виде суммы натурального числа и правильной дроби. Например, 11/5 = 2 + 1/5.

Как устроена обыкновенная дробь

Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.

Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.

Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.

Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим.

Черта между числителем и знаменателем — символ деления.

Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.

Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.

Как устроена десятичная дробь

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

• 0,3
• 4,23
• 9,939

Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Свойства дробей

Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:

где a, b, k — натуральные числа.

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:

У нас есть отличные курсы по математике для учеников с 1 по 11 классы, записывайтесь!

Действия с дробями

С дробями можно выполнять те же действия, что и с обычными числами: складывать, вычитать, умножать и делить. А еще дроби можно сокращать и сравнивать между собой. Давайте попробуем.

Сравнение дробей

Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.

Сравним 1/5 и 4/5. Как рассуждаем:

1. В обеих дробях знаменатель равен 5.
2. В первой дроби числитель равен 1, во второй дроби равен 4.

Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. А после приведения дробей к общему знаменателю, можно применить правило сравнения дробей с одинаковыми знаменателями.

Пример. Сравнить 2/7 и 1/14.

1. Приведем дроби к общему знаменателю:
   
2. Сравним дроби с одинаковыми знаменателями:
   

Важно запомнить: любая неправильная дробь больше любой правильной. Потому что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.

Чтобы сравнить дроби с разными числителями и знаменателями, нужно:

• привести дроби к наименьшему общему знаменателю (НОЗ);
• сравнить полученные дроби.

Чтобы привести дроби к наименьшему общему знаменателю, нужно:

1. Найти наименьшее общее кратное (НОК) знаменателей дробей, которое станет их общим знаменателем.
2. Разделить общий знаменатель на знаменатель данных дробей, то есть найти для каждой дроби дополнительный множитель.
3. Умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.

Сокращение дробей

Сокращение дроби — это деление числителя и знаменателя дроби на одно и то же натуральное число. Сократить дробь значит сделать ее короче и проще для восприятия. Например, дробь 1/3 выглядит намного проще и красивее, чем 27/81.

Сокращение дроби выглядит так: зачеркивают числитель и знаменатель, а рядом записывают результаты деления числителя и знаменателя на одно и то же число.

В этом примере делим обе части дроби на двойку.

Можно никуда не спешить и сокращать дроби последовательно, в несколько действий.

Сложение и вычитание дробей

При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.

Не забудьте проверить, можно ли сократить дробь и выделить целую часть.

При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).

Найдем наименьшее общее кратное для определения единого делителя.

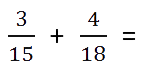
Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.

НОК (15, 18) = 3 * 2 * 3 * 5 = 90

Найдем дополнительные множители для каждой дроби. Для этого НОК делим на каждый знаменатель:

Полученные числа запишем справа сверху над числителем.

Воспользуемся одним из основных свойств дробей: перемножим делимое и делитель на дополнительный множитель. После умножения делитель должен быть равен наименьшему общему кратному, которое мы ранее высчитывали. Затем можно перейти к сложению.

Проверим полученный результат:

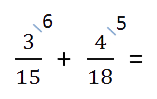
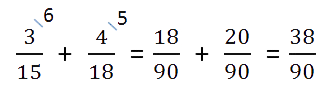
• если делимое больше делителя, нужно преобразовать в смешанное число;
• если есть что сократить, нужно выполнить сокращение.

Ход решения одной строкой:

Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:

1. Сложить целые части.
   
   
2. Сложить дробные части.
   

Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.

Суммировать полученные результаты.

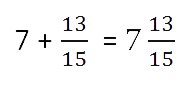
Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.

Умножение и деление дробей

Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:

Не забываем про сокращение. Это может облегчить вычисления.

Чтобы умножить два смешанных числа, надо:

1. преобразовать смешанные дроби в неправильные;
2. перемножить числители и знаменатели дробей;
3. сократить полученную дробь;
4. если получилась неправильная дробь, преобразовать в смешанную.

Чтобы разделить дробь на дробь нужно выполнить следующую последовательность действий:

• числитель первой умножить на знаменатель второй, результат произведения записать в числитель новой дроби;
• знаменатель первой умножить на числитель второй, результат произведения записать в знаменатель новой дроби.

Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.

Числа, произведение которых равно 1, называют взаимно обратными.

Как делить дроби с разными знаменателями? На самом деле одинаковые или разные знаменатели у дробей — неважно, потому что все дроби делятся по правилу, описанному выше.

Для деления смешанных чисел необходимо:

• представить числа в виде неправильных дробей;
• разделить то, что получилось друг на друга.

Дроби

Дробь — число, которое состоит из целого числа долей единицы и представляется в виде frac .

Числитель дроби (a) — число, находящееся над чертой дроби и показывающее количество долей, на которые была поделена единица.

Знаменатель дроби (b) — число, находящееся под чертой дроби и показывающее на сколько долей поделили единицу.

Содержание

Основное свойство дроби

Другими словами, мы получим дробь, равную данной, умножив или разделив числитель и знаменатель исходной дроби на одно и то же натуральное число.

Сокращение дроби — это процесс замены дроби, при котором новая дробь получается равной исходной, но с меньшим числителем и знаменателем.

Сокращать дроби принято, опираясь на основное свойство дроби.

Например, frac<45><60>=frac<15> <20>(числитель и знаменатель делится на число 3 ); полученную дробь снова можно сократить, разделив на 5 , то есть frac<15><20>=frac 34 .

Несократимая дробь — это дробь вида frac 34 , где числитель и знаменатель являются взаимно простыми числами. Основная цель сокращения дроби — сделать дробь несократимой.

Приведение дробей к общему знаменателю

Возьмем в качестве примера две дроби: frac<2> <3>и frac<5> <8>с разными знаменателями 3 и 8 . Для того, чтобы привести данные дроби к общему знаменателю и сначала перемножим числитель и знаменатель дроби frac<2> <3>на 8 . Получаем следующий результат: frac<2 cdot 8> <3 cdot 8>= frac<16> <24>. Затем умножаем числитель и знаменатель дроби frac<5> <8>на 3 . Получаем в итоге: frac<5 cdot 3> <8 cdot 3>= frac<15> <24>. Итак, исходные дроби приведены к общему знаменателю 24 .

Арифметические действия над обыкновенными дробями

Сложение обыкновенных дробей

а) При одинаковых знаменателях числитель первой дроби складывают с числителем второй дроби, оставляя знаменатель прежним. Как видно на примере:

б) При разных знаменателях дроби сначала приводят к общему знаменателю, а затем выполняют сложение числителей по правилу а) :

Вычитание обыкновенных дробей

а) При одинаковых знаменателях из числителя первой дроби вычитают числитель второй дроби, оставляя знаменатель прежним:

б) Если же знаменатели дробей различны, то сначала дроби приводят к общему знаменателю, а затем повторяют действия как в пункте а) .

Умножение обыкновенных дробей

Умножение дробей подчиняется следующему правилу:

то есть перемножают отдельно числители и знаменатели.

Деление обыкновенных дробей

Деление дробей производят следующим способом:

Взаимно обратные числа

Если ab=1 , то число b является обратным числом для числа a .

Пример: для числа 9 обратным является frac<1> <9>, так как 9 cdot frac<1><9>=1 , для числа 5 — frac<1> <5>, так как 5 cdot frac<1><5>=1 .

Десятичные дроби

Десятичной дробью называется правильная дробь, знаменатель которой равен 10, 1000, 10,000, . 10^n .

Таким же способом пишутся неправильные со знаменателем 10^n или смешанные числа.

В виде десятичной дроби представляется любая обыкновенная дробь со знаменателем, который является делителем некой степени числа 10 .

Пример: 5 — делитель числа 100 , поэтому дробь frac<1><5>=frac<1 cdot 20><5 cdot 20>=frac<20><100>=0,2 .

Арифметические действия над десятичными дробями

Сложение десятичных дробей

Для сложения двух десятичных дробей, нужно их расположить так, чтобы друг под другом оказались одинаковые разряды и запятая под запятой, а затем выполнить сложение дробей как обычных чисел.

Вычитание десятичных дробей

Выполняется аналогично сложению.

Умножение десятичных дробей

При умножении десятичных чисел достаточно перемножить заданные числа, не обращая внимания на запятые (как натуральные числа), а в полученном ответе запятой справа отделяется столько цифр, сколько их стоит после запятой в обоих множителях суммарно.

Давайте выполним умножение 2,7 на 1,3 . Имеем 27 cdot 13=351 . Отделяем справа две цифры запятой (у первого и второго числа — одна цифра после запятой; 1+1=2 ). В итоге получаем 2,7 cdot 1,3=3,51 .

Если в полученном результате получается меньше цифр, чем надо отделить запятой, то впереди пишут недостающие нули, например:

Для умножения на 10 , 100 , 1000 , надо в десятичной дроби перенести запятую на 1 , 2 , 3 цифры вправо (в случае необходимости справа приписывается определенное число нулей).

Например: 1,47 cdot 10,000 = 14 700 .

Деление десятичных дробей

Деление десятичной дроби на натуральное число производят также, как и деление натурального числа на натуральное. Запятая в частном ставится после того, как закончено деление целой части.

Если целая часть делимого меньше делителя, то в ответе получается нуль целых, например:

Рассмотрим деление десятичной дроби на десятичную. Пусть нужно разделить 2,576 на 1,12 . Первым делом, умножим делимое и делитель дроби на 100 , то есть перенесем запятую вправо в делимом и делителе на столько знаков, сколько их стоит в делителе после запятой (в данном примере на две). Затем нужно выполнить деление дроби 257,6 на натуральное число 112 , то есть задача сводится к уже рассмотренному случаю:

Бывает так, что не всегда получается конечная десятичная дробь при делении одного числа на другое. В результате получается бесконечная десятичная дробь. В таких случаях переходят к обыкновенным дробям.

Основное свойство дроби

Все обыкновенные дроби обладают следующим свойством:

Если числитель и знаменатель обыкновенной дроби умножить или разделить на одно и то же натуральное число, то получится дробь, равная данной.

Это свойство называется основным свойством дроби. С его помощью можно получать новые дроби, равные данной дроби.

В общем виде основное свойство дроби можно выразить так:

где a — нуль или натуральное число, b и m — натуральные числа.

Согласно данному свойству, одну и ту же часть единицы можно выразить с помощью дробей в разных формах.

Пример. Рассмотрим три круга, у которых жёлтым цветом закрашена некоторая одинаковая часть:

У первого круга закрашено круга, у второго — круга, у третьего — .

Все три дроби равны между собой , так как выражают одну и ту же часть круга, но их числители и знаменатели разные.

Можно заметить, что члены второй дроби в 2 раза больше числителя и знаменателя первой дроби, а члены третьей — в 3 раза.

Умножив оба члена дроби на 2, получим дробь :

Умножив оба члена дроби на 3, получим дробь :

Или наоборот, разделив числитель и знаменатель дроби на 3, получим дробь :

Разделив члены дроби на 2, получим дробь :

Умножение числителя и знаменателя дроби на одно и то же число называют расширением дроби. Деление числителя и знаменателя на одно и то же число называют сокращением дроби.

Основное свойство дроби обычно применяется при сокращении дробей и при приведении дробей к общему знаменателю.

Алгебра. Урок 1. Числа и вычисления

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

• Смешанная дробь

• Десятичная дробь

• Сложение и вычитание дробей

• Умножение и деление дробей

• Сравнение дробей

• Степень числа

• Свойства степеней

• Возведение отрицательных чисел в степень

Действия с дробями

Понятие обыкновенной, десятичной, смешанной дроби.

Обыкновенная дробь – дробь вида

где число a – числитель дроби, число b – знаменатель.
Примеры:

1 2 ; 6 5 ; 3 1 ; 7 15 .

Обыкновенная дробь может быть правильной или неправильной, сократимой или несократимой:

Дробь называется правильной , если числитель ( a ) меньше знаменателя ( b ) .
Примеры:

Дробь называется неправильной , если числитель ( a ) больше знаменателя ( b ) .
Примеры:

Основное свойство обыкновенной дроби:

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число (натуральные числа – числа, которые используются при счете: 1, 2, 3, …), то получится дробь, равная данной.

Дробь называется сократимой , если числитель и знаменатель имеют общие множители (числитель и знаменатель можно поделить на одно и то же число).
Примеры сократимых дробей:

12 16 = 3 ? 4 4 ? 4 = 3 4

21 14 = 3 ? 7 2 ? 7 = 3 2

Дробь называется несократимой , если числитель и знаменатель дроби не имеют общих множителей.
Примеры несократимых дробей:

2 5 ; 9 11 ; 125 126 .

Дробь называется смешанной , если у нее есть целая часть. То есть саму дробь можно представить в виде суммы целого числа и обыкновенной дроби.
Примеры смешанных дробей:

3 1 2 ; 2 7 8 ; 90 12 77 .

Смешанную дробь всегда можно перевести в неправильную обыкновенную дробь.

3 1 2 = 3 ⋅ 2 + 1 2 = 7 2

2 7 8 = 2 ⋅ 8 + 7 8 = 23 8

90 12 77 = 90 ⋅ 77 + 12 77 = 6942 77

Дробь называется десятичной , если она представлена в десятичной записи.
Примеры десятичных дробей:

56,002 ; 4,125 ; 12,3 ; 0,01 .

Десятичную дробь всегда можно перевести в смешанную дробь или в обыкновенную дробь с числителем и знаменателем. Так поступают, когда необходимо совершить действие между обыкновенной дробью и десятичной.

Перевод в смешанные дроби:

56,002 = 56 2 1000 = 56 1 500

56,002 = 56 2 1000 = 56 1 500

Перевод в обыкновенные дроби:

12 , 3 = 12 3 10 = 12 ⋅ 10 + 3 10 = 123 10 0 , 01 = 1 100

Сложение и вычитание дробей.

Для того, чтобы складывать и вычитать смешанные дроби между собой, необходимо действовать следующим образом:

• превратить дроби из смешанных в неправильные, если такие дроби есть,
  например: [2frac<7><8>= frac<<2 cdot 8 + 7>><8>= frac<<23>><8>]
• найти наименьший общий знаменатель у полученных дробей и домножить числители на недостающие множители;
• произвести сложение или вычитание числителей дробей, подписав под суммой или разностью общий знаменатель.

(1) 2 1 6 + 1 7 8 = 2 ⋅ 6 + 1 6 + 1 ⋅ 8 + 7 8 = 13 6 + 15 8 = 13 ⋅ 4 6 ⋅ 4 + 15 ⋅ 3 8 ⋅ 3 = 52 + 45 24 = 97 24 = 4 1 24

(2) 3 7 12 − 2 3 16 = 3 ⋅ 12 + 7 12 − 2 ⋅ 16 + 3 16 = 43 12 − 35 16 = 43 ⋅ 4 12 ⋅ 4 − 35 ⋅ 3 16 ⋅ 3 = 172 − 105 48 = 67 48 = 1 19 48

(3) 2 3 14 − 0,6 = 2 ⋅ 14 + 3 14 − 6 10 = 31 14 − 3 5 = 31 ⋅ 5 14 ⋅ 5 − 3 ⋅ 14 5 ⋅ 14 = 155 − 42 70 = 113 70 = 1 43 70

Умножение и деление дробей.

При умножении двух дробей числитель первой дроби умножается на числитель второй дроби, знаменатель первой дроби умножается на знаменатель второй:

Чтобы умножить дробь на число , необходимо представить это число в виде дроби со знаменателем-единицей:

При делении двух дробей необходимо первую дробь умножить на «перевёрнутую» предыдущую, то есть у дроби-делителя поменять местами числитель и знаменатель и поставить операцию умножения вместо операции деления между этими дробями:

Чтобы разделить дробь на число , необходимо представить это число в виде дроби со знаменателем-единицей:

(1) 2 3 4 ⋅ 8 11 ÷ 0,5 = 11 1 4 1 ⋅ 8 2 11 1 ÷ 5 1 10 2 = 2 ÷ 1 2 = 2 ⋅ 2 1 = 4

(2) 6 ÷ 2,25 ⋅ 1,5 = 6 1 ÷ 2 1 4 ⋅ 1 5 1 10 2 = 6 1 ÷ 9 4 ⋅ 3 2 = 6 3 1 ⋅ 4 9 3 ⋅ 3 1 2 1 = 4

Сравнение дробей.

Для того, чтобы сравнивать две дроби между собой, нужно уметь выполнять действия с дробями (сложение, вычитание, умножение, деление). При сравнении дробей, особенно в заданиях, где требуется расположить дроби в порядке возрастания или убывания, удобно приводить обыкновенную дробь к виду десятичной.

Сравнение дробей с одинаковыми знаменателями

Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.
Примеры:

[frac<4> <7>frac<1><<14>>;;;;; frac<2> <3>Сравнение дробей с одинаковыми числителями

Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше.
Примеры:

[frac<2> <7>frac<7><<11>>;;;;; frac<5> <4>> frac<5><5>.] Сравнение дробей с разными числителями и знаменателями

Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю.
Пример 1:

Приводим дроби к общему знаменателю:

Приходим к выводу, что:

Действия со степенями.

$a^n$ — степень числа $a$ с натуральным показателем $n$.

$a$ — основание степени, $n$ — показатель.

a n = a ⋅ a ⋅ . ⋅ a ︸ n р а з — произведение $n$ множителей, каждый из которых равен $a$.

Любое число $a$ можно представить в виде $a=a^1$. То есть $2=2^1$, $15=15^1$ и так далее.

Единицу можно представить, как произвольное число в степени $0$, то есть $1=2^0=15^0dotsc$

Единицу можно возводить в любую степень, то есть $1=1^n=1^0=1^1=1^8=1^<146>dotsc$

Ноль в любой натуральной степени есть ноль, то есть: $0 = <0^n>= <0^1>= <0^<15>> = <0^<179>>dotsc$ где $n ne 0$.

Запись 0 0 в математике не имеет смысла.

Свойства степеней с натуральным показателем:

Обыкновенные дроби

Урок 3. Подготовка к ОГЭ по математике 9 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока “Обыкновенные дроби”

· повторить понятие «обыкновенная дробь», виды обыкновенных дробей;

· повторить основное свойство дроби;

· вспомнить, как неправильную дробь можно представить в виде смешанной или целого числа, а также как смешанную дробь можно представить в виде неправильной;

· повторить порядок выполнения действий над обыкновенными дробями.

Мы ранее рассматривали случаи, когда нельзя выполнить целочисленное деление. В таких ситуациях можно частное записать в виде дроби. Делимое тогда называют числителем, а делитель — знаменателем. Отделяет их друг от друга черта дроби.

Как вам известно выделяют правильные и неправильные обыкновенные дроби. Напомним их отличия.

Напомним основное свойство дроби.

Числитель и знаменатель дроби можно умножать и делить на одно и тоже число, при этом значение дроби останется тем же.

Определение.

Умножение числителя и знаменателя на некоторое число называют приведением к новому знаменателю. Это позволяет приводить дроби к общему знаменателю.

Обычно дроби приводят к наименьшему общему знаменателю. Он равен наименьшему общему кратному знаменателей данных дробей.

Определение.

Процесс деления числителя и знаменателя на некоторое число мы привыкли называть сокращением.

Обычно сократимую дробь сокращают на наибольший общий делитель числителя и знаменателя. Тем самым в итоге получают несократимую дробь. И к такому виду принято приводить все дроби, полученные в результате вычислений, прежде чем записать ответ. Дробь является несократимой, если числитель и знаменатель являются взаимно простыми числами.

А теперь сократим дроби.

Вам хорошо известно, что у любой неправильной дроби можно выделить целую часть.

Напомним, как это можно сделать.

Можно разделить числитель на знаменатель с остатком.

Частное будет целой частью, остаток — числителем дробной части, а исходный знаменатель — знаменателем дробной части.

Так из неправильной дроби мы получим смешанную.

Далее вспомним правила сравнения обыкновенных дробей.

Если же у дробей разные числители и разные знаменатели, то пользуясь основным свойством дроби их можно привести или к равным знаменателям, или к равным числителям.

В работе с дробями нужно уметь не только выделять целую часть у неправильных дробей, а ещё и представлять смешанные дроби в виде неправильных. Напомним, как это можно сделать.

Для этого в числитель записывают произведение целой части и знаменателя, увеличенного на числитель исходной дроби. Ну, а знаменатель оставляют тем же.

Далее подробнее поговорим о выполнении арифметических действий с дробями.

Складывая дроби с одинаковыми знаменателями, в числитель записываем сумму числителей, а знаменатель оставляем тем же.

Если же нужно сложить дроби с разными знаменателями, предварительно их нужно привести к общему и сложить полученные дроби.

Вычитание дробей с одинаковыми знаменателями проводят по аналогичному правилу. В числитель записывают разность числителей, а знаменатель оставляют тем же.

Для вычитания дробей с разными знаменателями, их сначала нужно привести к общему знаменателю, а затем вычислить разность полученных дробей.

Теперь поговорим об умножении дробей.

Чтобы умножить дробь на число нужно только числитель умножить на это число, а знаменатель оставить тем же.

Произведением двух дробей является дробь, у которой числитель равен произведению числителей исходных дробей, а знаменатель — произведению знаменателей исходных дробей.

К тому же вам известно, что, если среди дробей множителей есть смешанные дроби, то их нужно предварительно представить в виде неправильных.

А теперь самое время вспомнить понятие взаимно обратных чисел.

Определение.

Взаимно обратными называют 2 числа, произведение которых равно единице.

Вернёмся к действиям с дробями и рассмотрим последнее — деление дробей.

Прежде чем приступить к делению, смешанные дроби так же нужно представлять в виде неправильных, и далее пользоваться таким правилом.

Знак деления нужно заменить умножением и дробь-делитель заменить обратной ей дробью. А далее следовать по правилу умножения дробей.

Подводя итоги урока, вспомним, какие вопросы мы на нём осветили.

Мы вспомнили, что обыкновенные дроби бывают правильными и неправильными, а также повторили основное свойство дроби, которое позволяет сокращать дроби и приводить их к новому знаменателю.

Вспомнили, как неправильную дробь можно представить в виде смешанной или в виде целого числа, а также как смешанную дробь можно представить в виде неправильной.

И, освежив в памяти правила выполнения действий над обыкновенными дробями, мы применили их при вычислении значений выражений.

Периметр равностороннего треугольника

Средняя оценка: 4.4

Всего получено оценок: 305.

Средняя оценка: 4.4

Всего получено оценок: 305.

Равносторонний треугольник занимает особое место среди треугольников. Для того, чтобы найти значение периметра, площади, углов или радиусов окружностей вписанной и описанной у равнобедренного треугольника, достаточно знать величину стороны. С одной стороны, это значительно облегчает решение, с другой составители задач редко дают значение стороны и приходится искать обходные пути решения.

Формула нахождения периметра равностороннего треугольника

Формула периметра равностороннего треугольника вытекает из определений. Что такое периметр? Периметр это сумма всех сторон фигуры. Равносторонний треугольник – это треугольник, все стороны которого равны.

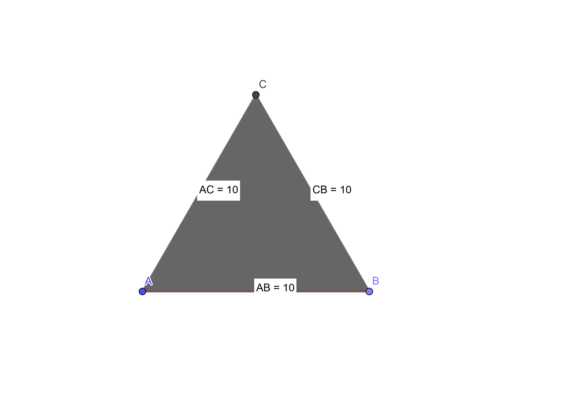Рис. 1. Равносторонний треугольник

Значит,для того, чтобы найти значение периметра достаточно умножить величину стороны на количество сторон:

Решим несколько разных по сложности задач, чтобы разобраться, какие проблемы могут встречаться на пути нахождения периметра.

Задача 1

• В равностороннем треугольнике сторона равна 6. Найти периметр треугольника.

Это самый простой вариант задачи. Достаточно подставить значение в формулу и получить результат. Такая задача не должна вызывать затруднений:

Задача 2

• В равнобедренном треугольнике острый угол при основании равен 60 градусам, площадь треугольника равна $$<64oversqrt<3>>$$.

Особое внимание нужно обращать на вид фигуры, который указан в условии задачи.

В данной задаче дан равнобедренный треугольник. Чтобы воспользоваться общей формулой, необходимо доказать, что этот равнобедренный треугольник является еще и равносторонним.

Обратим внимание на величину угла. Угол при основании равен 60. При этом углы у основания равнобедренного треугольника равны, а сумма углов любого треугольника равна 180 градусов. Значит у основания два угла по 60 градусов. Рассчитаем угол при вершине:

180-60-60=60 – угол при вершине так же равен 60 градусам.

Значит, данный треугольник будет равносторонним, так как все углы равны 60 градусам.

Углы по 60 градусов характерны только для равностороннего треугольника. Именно сочетание 3 равных сторон образует 3 равных угла. В любых других ситуациях, хотя бы один угол будет отличаться.

Для площади равностороннего треугольника имеется отдельная формула:

$$S=a^2*over 4>=<64oversqrt<3>>$$ – где а значение стороны, которое нам и нужно выразить из этой формулы.

Подставим полученное значение в формулу:

Задача 3

• В равностороннем треугольнике высота равна $$3*sqrt<3>$$. Найти периметр треугольника.

Для данной задачи нужно воспользоваться методом решения, который часто используется в задачах с равнобедренным треугольником. Из любой вершины опустим высоту, которая будет медианой и биссектрисой.

В одном из получившихся треугольников выразим значение высоты через сторону с помощью теоремы Пифагора:

Вычтем подобные слагаемые:

Из получившейся формулы выразим значение стороны:

Рис. 3. Периметр равностороннего треугольника

Подставим получившееся значение в формулу периметра равностороннего треугольника.

Что мы узнали?

Мы обсудили формулу для нахождения периметра равностороннего треугольника. Выделили проблемы, которые приходится решать при нахождении стороны равностороннего треугольника для дальнейшего решения задачи. Рассмотрели различные пути решения задач на нахождение периметра равностороннего треугольника.