Монотонность функции как определить убывающую и возрастающую

Монотонность функции как определить убывающую и возрастающую

Пусть (y = fleft( x right)) является дифференцируемой функцией на интервале (left( right).) Функция называется возрастающей (или неубывающей ) на данном интервале, если для любых точек (, in left( right),) таких, что ( строго возрастающей на интервале (left( right).)

Аналогично определяются убывающая (или невозрастающая ) и строго убывающая функции.

Введенные понятия можно сформулировать в более компактной форме. Функция (y = fleft( x right)) называется

возрастающей ( неубывающей ) на интервале (left( right),) если [ , in left( right):;><строго возрастающей на интервале (left( right),) если [ , in left( right):;><убывающей ( невозрастающей ) на интервале (left( right),) если [ , in left( right):;><строго убывающей на интервале (left( right),) если [ , in left( right):;><Рис.1

Если функция (fleft( x right)) дифференцируема на интервале (left( right)) и принадлежит к одному из четырех рассмотренных типов (т.е. является возрастающей, строго возрастающей, убывающей или строго убывающей), то такая функция называется монотонной на данном интервале.

Понятия возрастания и убывания функции можно определить также и для отдельной точки (.) В этом случае рассматривается малая (delta)-окрестность (left( <– delta , + delta > right)) этой точки. Функция (y = fleft( x right)) является строго возрастающей в точке (,) если существует число (delta > 0,) такое, что [forall;x in left( <– delta ,> right) Rightarrow fleft( x right) fleft( <> right).] Аналогичным образом определяется строгое убывание функции (y = fleft( x right)) в точке (.)

Снова рассмотрим функцию (y = fleft( x right),) считая ее дифференцируемой на некотором интервале (left( right).) Возрастание или убывание функции на интервале определяется по знаку первой производной функции.

Теорема 1 .
Для того, чтобы функция (y = fleft( x right)) была возрастающей на интервале (left( right),) необходимо и достаточно, чтобы первая производная функции была неотрицательной всюду на данном интервале: [f’left( x right) ge 0;forall;x in left( right).] Аналогичный критерий действует для случая функции, убывающей на интервале (left( right):) [f’left( x right) le 0;forall;x in left( right).] Докажем обе части теоремы (необходимость и достаточность) для случая возрастающей функции.

Поскольку (f’left( c right) ge 0,) то правая часть равенства неотрицательна. Следовательно, [fleft( <> right) ge fleft( <> right).] т.е. функция (y = fleft( x right)) является возрастающей на интервале (left( right).)

Рассмотрим теперь случаи строгого возрастания и строгого убывания функции. Здесь существует похожая теорема, описывающая необходимые и достаточные условия. Опуская доказательство, сформулируем ее для случая строго возрастающей функции.

Теорема 2 .
Для того, чтобы дифференцируемая на интервале (left( right)) функция была строго возрастающей на этом интервале, необходимо и достаточно, чтобы выполнялись следующие условия:

(f’left( x right) ge 0;forall;x in left( right);)

Производная (f’left( x right)) тождественно не равна нулю ни в каком промежутке (left[ <,> right] in left( right).)

Условие (1) содержится в теореме (1) и является признаком неубывающей функции. Дополнительное условие (2) требуется для того, чтобы исключить участки постоянства функции, в которых производная функции (fleft( x right)) тождественно равна нулю.

На практике (при нахождении интервалов монотонности) обычно используется достаточное условие строгого возрастания или строгого убывания функции. Из теоремы (2) следует такая формулировка достаточного признака:

Если для всех (x in left( right)) выполняется условие (f’left( x right) > 0) всюду в интервале (left( right),) кроме возможно лишь некоторых отдельных точек, в которых (f’left( x right) = 0,) то функция (fleft( x right)) является строго возрастающей .

Соответственно, условие (f’left( x right) строго убывающую функцию.

Число точек, в которых (f’left( x right) = 0,) является, как правило, конечным. Согласно теореме (2), они не могут плотно заполнять какой-либо промежуток в интервале (left( right).)

Приведем также признак строгого возрастания (убывания) функции в точке:

Если (f’left( <> right) > 0), то функция (fleft( x right)) строго возрастает в точке ();

Если (f’left( <> right) сумма функций (f + g) также возрастает (убывает) на этом интервале.

Если функция (f) возрастает (убывает) на интервале (left( right),) то противоположная функция (-f) убывает (возрастает) на этом интервале.

Если функция (f) возрастает (убывает) на интервале (left( right),) то обратная функция (largefrac<1>normalsize) убывает (возрастает) на этом интервале.

Если функции (f) и (g) возрастают (убывают) на интервале (left( right)) и, кроме того, (f ge 0), (g ge 0), то произведение функций (fg) также возрастает (убывает) на этом интервале.

Если функция (g) возрастает (убывает) на интервале (left( right),) а функция (f) возрастает (убывает) на интервале (left( right),) где (g:left( right) to left( right),) то композиция функций (f circ g) (т.е. сложная функция (y = fleft( right)) также возрастает (убывает) на интервале (left( right).)

Возьмем две произвольные точки () и (,) такие что [0 le lt .] Рассмотрим разность значений функции в этих точках: [ > right) – fleft( <> right) > = right) – left( right) > = = – > right)left( <+ > right).> ] В последнем выражении, очевидно, что ( <– > > 0) и ( <+ > > 0) (поскольку по условию рассматриваются неотрицательные значения (x)). В результате получаем: [ – > right)left( <+ > right) > 0,>;; > right) – fleft( <> right) > 0.> ] Это означает по определению, что функция (fleft( x right) = + 1) является строго возрастающей на заданном интервале.

Выберем две произвольные точки (<>) и (<>,) такие что ( формуле разности кубов , получаем: [ = – > right)left( + x_1^2> right).> ] Во второй скобке можно выделить полный квадрат: [ + x_1^2 > = cdot frac<<>> <2>+ frac<> <4>+ frac<<3x_2^2>> <4>> = <+ frac<<>><2>> right)^2> + frac<<3x_2^2>> <4>> 0.> ] Отсюда видно, что квадратичное выражение всегда положительно (оно равно нулю лишь при ( = = 0,) что противоречит условию ( 0,) если ( – > 0,) т.е. функция (fleft( x right) = ) является строго возрастающей.

Данная функция является суммой функций () и (3.)

Первую функцию () можно рассматривать как произведение двух одинаковых функций (). Из примера (1) следует, что квадратичная функция () строго возрастает при (x ge 0.) Следовательно, функция () также строго возрастает при (x ge 0) на основании свойства (4).

Второе слагаемое (3) представляет собой трехкратную сумму функций () и, поэтому, также является строго возрастающей (на основании свойства (1)).

Итак, исходная функция (fleft( x right) = + 3) является суммой двух строго возрастающих функций и, следовательно, также строго возрастает при (x ge 0.)

Для контроля рассмотрим также неравенство (f’left( x right) Рис.5

Таким образом, функция убывает (в строгом смысле) в интервалах (left( < - infty , - 1>right)) и (left( <1, infty>right)) и возрастает в промежутке (left( <-1, 1>right).) Учитывая, что корень функции равен (x = 0,) можно схематически нарисовать ее график (рисунок (6)).

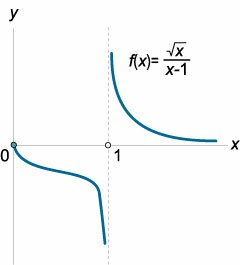
Следовательно, на основании достаточного признака монотонности, функция строго возрастает при (x in left( normalsize,infty > right)) и строго убывает при (x in left( <0, largefrac<1>normalsize> right).) Ее вид схематически приведен на рисунке (10).

На основании достаточного признака монотонности заключаем, что функция возрастает при (x in left( <0,largefrac<1><2>normalsize> right)) и убывает при (x in left( <2>normalsize,1> right).) График функции представляет собой полуокружность с центром в точке (left( <2>normalsize,0> right)) и радиусом (<2>normalsize>) (рисунок (14)).

Алгебра и начала математического анализа. 11 класс

Конспект урока

Алгебра и начала математического анализа, 11 класс

Урок №15. Возрастание и убывание функции.

Перечень вопросов, рассматриваемых в теме

1) Нахождение промежутков монотонности функции,

2) Определение алгоритма нахождения промежутков возрастания и убывания функции,

3) Решение задачи на нахождения промежутков возрастания и убывания функции

Глоссарий по теме

Алгоритм нахождения промежутков возрастания и убывания функции y = f(x)

1. Найти D(f)
2. Найти f‘(x).
3. Определить, при каких значениях хf‘(x) ≥ 0 (на этих промежутках функция возрастает); при каких значениях х f‘(x) ≤ 0 (на этих промежутках функция убывает))

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.

Теоретический материал для самостоятельного изучения

1. Функция y = f(x), определенная на промежутке Х, называется возрастающей на этом промежутке, если для любой пары чисел х₁ и х₂ из этого промежутка из неравенства х₁ f(x₂)

1. Если во всех точках открытого промежутка Х выполняется неравенство f‘(x) ≥ 0 (причем равенство f‘(x) = 0 либо не выполняется, либо выполняется лишь в конечном множестве точек),то функция y = f(x) возрастает на промежутке Х.
2. Если во всех точках открытого промежутка Х выполняется неравенство f‘(x) ≤ 0 (причем равенство f‘(x) = 0 либо не выполняется, либо выполняется лишь в конечном множестве точек),то функция y = f(x) убывает на промежутке Х.

Примеры и разбор решения заданий тренировочного модуля

№1. Определите промежутки монотонности функции

у = -3х 3 + 4х 2 + х – 10.

1.Найдем область определения функции.

D(y) =

2.Найдем производную функции.

3.Определим, на каких промежутках производная положительна (на этих промежутках функция возрастает), на каких – отрицательна (на этих промежутках функция убывает).

Применим для этого метод интервалов. Для определения знака на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной.

Так как на интервале производная функции отрицательна, то на этом интервале функция убывает.

Так как на интервале производная функции положительна, то на этом интервале функция возрастает.

Так как на интервале производная функции отрицательна, то на этом интервале функция убывает.

Так как в точках функция непрерывна, то эти точки входят в промежутки возрастания и убывания данной функции.

Следовательно, функция возрастает на ; функция убывает на и на .

Ответ: Функция возрастает на

Функция убывает на и на .

№2. Определите промежутки монотонности функции

у = х 5 –5х 4 +5х 3 – 4.

1. 
2. 

y‘ =

1. Функция возрастает на ; функция убывает на .

Ответ: Функция возрастает на ;

функция убывает на .

Возрастание и убывание функций

1) Функция y=f(x) называется возрастающей на некотором промежутке, если бо́льшему значению аргумента из этого промежутка соответствует бо́льшее значение функции.

То есть для любых двух значений x₁,x₂ из этого промежутка выполняется условие

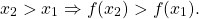x_1 Rightarrow f(x_2 ) > f(x_1 ). ]” title=”Rendered by QuickLaTeX.com”/>

2) Функция y=f(x) называется убывающей на некотором промежутке, если бо́льшему значению аргумента из этого промежутка соответствует меньшее значение функции.

То есть для любых двух значений x₁,x₂ из этого промежутка выполняется условие

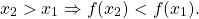x_1 Rightarrow f(x_2 )

Предполагается, что промежуток принадлежит области определения функции y=f(x). Обычно промежуток — это отрезок, интервал или полуинтервал.

График функции на промежутках возрастания «идёт вверх» (чем правее x, тем выше y).

На промежутках убывания график «идёт вниз» (чем правее x, тем ниже y).

Пользуясь графиком, найти промежутки возрастания и убывания функции y=f(x), определённой на отрезке [x₁;x₅]:

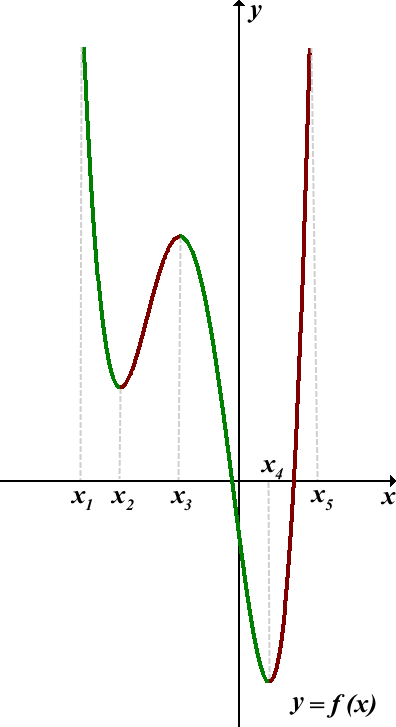
Кратко это записывают так:

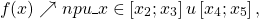
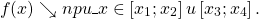
3) Функцию, возрастающую на промежутке либо убывающую на промежутке, называют монотонной функцией на этом промежутке (или строго монотонной).

4) Если функция возрастает на всей своей области определения, то её называют возрастающей.

Если функция убывает на всей своей области определения, то её называют убывающей.

Например, y=√x, y=x³ — возрастающие функции.

Линейная функция y=kx+b возрастающая при k>0 и убывающая при k 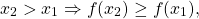x_1 Rightarrow f(x_2 ) ge f(x_1 ), ]” title=”Rendered by QuickLaTeX.com”/>

то функция y=f(x) называется неубывающей на этом промежутке.

6) Если для любых двух значений x₁,x₂ из некоторого промежутка выполняется условие

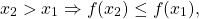x_1 Rightarrow f(x_2 ) le f(x_1 ), ]” title=”Rendered by QuickLaTeX.com”/>

то функция y=f(x) называется невозрастающей на этом промежутке.

7) Функцию, невозрастающую на промежутке либо неубывающую на промежутке, называют не строго монотонной функцией на этом промежутке.

Пользуясь графиком, найти промежутки, на которых функции y=g(x), определённая на отрезке [x₁;x₃], является невозрастающей и неубывающей:

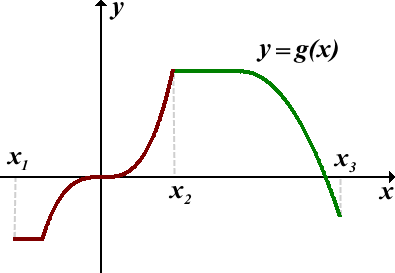
Функция y=g(x) является неубывающей на промежутке [x₁;x₂].

Функция y=g(x) является невозрастающей на промежутке [x₂;x₃].

Возрастание и убывание функции можно определять как с помощью графика, так и аналитически.

Как доказать, что функция возрастает или убывает, с помощью задающей эту функцию формулы?

группирует первое слагаемое с третьим, второе — с четвертым. В первых скобках — разность квадратов, из вторых выносим общий множитель 4 за скобки:

Теперь выносим общий множитель (x₂-x₁) за скобки:

Так как x₂>x₁, то x₂-x₁>0. Следовательно, знак произведения зависит от знака второго множителя.

Для x₁, x₂ ∈(-∞;-2) x₂+x₁+4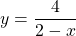

возрастает на промежутке (2;+∞).

Функция определена при x∈(-∞;2) и (2;+∞).

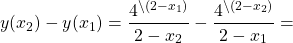
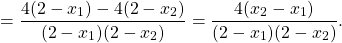
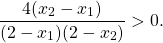0. ]” title=”Rendered by QuickLaTeX.com”/>

Отсюда y(x₂)-y(x₁)>0. Поэтому данная функция возрастает на промежутке (2;+∞).

Что и требовалось доказать.

Исследование функции на монотонность гораздо удобнее проводить с помощью производной (начала математического анализа — производную и её применение — проходят в школьном курсе алгебры в 10-11 классах).

Возрастание и убывание функции на интервале, экстремумы

Чтобы определить характер функции и говорить о ее поведении, необходимо находить промежутки возрастания и убывания. Этот процесс получил название исследования функции и построения графика. Точка экстремума используется при нахождении наибольшего и наименьшего значения функции, так как в них происходит возрастание или убывание функции из интервала.

Данная статья раскрывает определения, формулируем достаточный признак возрастания и убывания на интервале и условие существования экстремума. Это применимо к решению примеров и задач. Следует повторить раздел дифференцирования функций, потому как при решении необходимо будет использовать нахождение производной.

Возрастание и убывание функции на интервале

Функция y = f ( x ) будет возрастать на интервале x , когда при любых x 1 ∈ X и x 2 ∈ X , x 2 > x 1 неравенство f ( x 2 ) > f ( x 1 ) будет выполнимо. Иначе говоря, большему значению аргумента соответствует большее значение функции.

Функция y = f ( x ) считается убывающей на интервале x , когда при любых x 1 ∈ X , x 2 ∈ X , x 2 > x 1 равенство f ( x 2 ) > f ( x 1 ) считается выполнимым. Иначе говоря, большему значению функции соответствует меньшее значение аргумента. Рассмотрим рисунок, приведенный ниже.

Замечание: Когда функция определенная и непрерывная в концах интервала возрастания и убывания, то есть ( a ; b ) , где х = а , х = b , точки включены в промежуток возрастания и убывания. Определению это не противоречит, значит, имеет место быть на промежутке x .

Основные свойства элементарных функций типа y = sin x – определенность и непрерывность при действительных значениях аргументах. Отсюда получаем, что возрастание синуса происходит на интервале – π 2 ; π 2 , тогда возрастание на отрезке имеет вид – π 2 ; π 2 .

Точки экстремума, экстремумы функции

Точка х 0 называется точкой максимума для функции y = f ( x ) , когда для всех значений x неравенство f ( x 0 ) ≥ f ( x ) является справедливым. Максимум функции – это значение функции в точке, причем обозначается y m a x .

Точка х 0 называется точкой минимума для функции y = f ( x ) , когда для всех значений x неравенство f ( x 0 ) ≤ f ( x ) является справедливым. Минимум функции – это значение функции в точке, причем имеет обозначение вида y m i n .

Окрестностями точки х 0 считаются точки экстремума, а значение функции, которое соответствует точкам экстремума. Рассмотрим рисунок, приведенный ниже.

Экстремумы функции с набольшим и с наименьшим значением функции. Рассмотрим рисунок, приведенный ниже.

Первый рисунок говорит о том, что необходимо найти наибольшее значение функции из отрезка [ a ; b ] . Оно находится при помощи точек максимума и равняется максимальному значению функции, а второй рисунок больше походит на поиск точки максимума при х = b .

Достаточные условия возрастания и убывания функции

Чтобы найти максимумы и минимумы функции, необходимо применять признаки экстремума в том случае, когда функция удовлетворяет этим условиям. Самым часто используемым считается первый признак.

Первое достаточное условие экстремума

Пусть задана функция y = f ( x ) , которая дифференцируема в ε окрестности точки x 0 , причем имеет непрерывность в заданной точке x 0 . Отсюда получаем, что

• когда f ‘ ( x ) > 0 с x ∈ ( x 0 – ε ; x 0 ) и f ‘ ( x ) 0 при x ∈ ( x 0 ; x 0 + ε ) , тогда x 0 является точкой максимума;
• когда f ‘ ( x ) 0 с x ∈ ( x 0 – ε ; x 0 ) и f ‘ ( x ) > 0 при x ∈ ( x 0 ; x 0 + ε ) , тогда x 0 является точкой минимума.

Иначе говоря, получим их условия постановки знака:

• когда функция непрерывна в точке x 0 , тогда имеет производную с меняющимся знаком, то есть с + на – , значит, точка называется максимумом;
• когда функция непрерывна в точке x 0 , тогда имеет производную с меняющимся знаком с – на + , значит, точка называется минимумом.

Алгоритм для нахождения точек экстремума

Чтобы верно определить точки максимума и минимума функции, необходимо следовать алгоритму их нахождения:

• найти область определения;
• найти производную функции на этой области;
• определить нули и точки, где функция не существует;
• определение знака производной на интервалах;
• выбрать точки, где функция меняет знак.

Рассмотрим алгоритм на примере решения нескольких примеров на нахождение экстремумов функции.

Найти точки максимума и минимума заданной функции y = 2 ( x + 1 ) 2 x – 2 .

Область определения данной функции – это все действительные числа кроме х = 2 . Для начала найдем производную функции и получим:

y ‘ = 2 x + 1 2 x – 2 ‘ = 2 · x + 1 2 ‘ · ( x – 2 ) – ( x + 1 ) 2 · ( x – 2 ) ‘ ( x – 2 ) 2 = = 2 · 2 · ( x + 1 ) · ( x + 1 ) ‘ · ( x – 2 ) – ( x + 1 ) 2 · 1 ( x – 2 ) 2 = 2 · 2 · ( x + 1 ) · ( x – 2 ) – ( x + 2 ) 2 ( x – 2 ) 2 = = 2 · ( x + 1 ) · ( x – 5 ) ( x – 2 ) 2

Отсюда видим, что нули функции – это х = – 1 , х = 5 , х = 2 , то есть каждую скобку необходимо приравнять к нулю. Отметим на числовой оси и получим:

Теперь определим знаки производной из каждого интервала. Необходимо выбрать точку, входящую в интервал, подставить в выражение. Например, точки х = – 2 , х = 0 , х = 3 , х = 6 .

y ‘ ( – 2 ) = 2 · ( x + 1 ) · ( x – 5 ) ( x – 2 ) 2 x = – 2 = 2 · ( – 2 + 1 ) · ( – 2 – 5 ) ( – 2 – 2 ) 2 = 2 · 7 16 = 7 8 > 0 , значит, интервал – ∞ ; – 1 имеет положительную производную. Аналогичным образом получаем, что

y ‘ ( 0 ) = 2 · ( 0 + 1 ) · 0 – 5 0 – 2 2 = 2 · – 5 4 = – 5 2 0 y ‘ ( 3 ) = 2 · ( 3 + 1 ) · ( 3 – 5 ) ( 3 – 2 ) 2 = 2 · – 8 1 = – 16 0 y ‘ ( 6 ) = 2 · ( 6 + 1 ) · ( 6 – 5 ) ( 6 – 2 ) 2 = 2 · 7 16 = 7 8 > 0

Так как второй интервал получился меньше нуля, значит, производная на отрезке будет отрицательной. Третий с минусом, четвертый с плюсом. Для определения непрерывности необходимо обратить внимание на знак производной, если он меняется, тогда это точка экстремума.

Получим, что в точке х = – 1 функция будет непрерывна, значит, производная изменит знак с + на – . По первому признаку имеем, что х = – 1 является точкой максимума, значит получаем

y m a x = y ( – 1 ) = 2 · ( x + 1 ) 2 x – 2 x = – 1 = 2 · ( – 1 + 1 ) 2 – 1 – 2 = 0

Точка х = 5 указывает на то, что функция является непрерывной, а производная поменяет знак с – на +. Значит, х=-1 является точкой минимума, причем ее нахождение имеет вид

y m i n = y ( 5 ) = 2 · ( x + 1 ) 2 x – 2 x = 5 = 2 · ( 5 + 1 ) 2 5 – 2 = 24

Графическое изображение

Ответ: y m a x = y ( – 1 ) = 0 , y m i n = y ( 5 ) = 24 .

Стоит обратить внимание на то, что использование первого достаточного признака экстремума не требует дифференцируемости функции с точке x 0 , этим и упрощает вычисление.

Найти точки максимума и минимума функции y = 1 6 x 3 = 2 x 2 + 22 3 x – 8 .

Область определения функции – это все действительные числа. Это можно записать в виде системы уравнений вида:

– 1 6 x 3 – 2 x 2 – 22 3 x – 8 , x 0 1 6 x 3 – 2 x 2 + 22 3 x – 8 , x ≥ 0

После чего необходимо найти производную:

y ‘ = 1 6 x 3 – 2 x 2 – 22 3 x – 8 ‘ , x 0 1 6 x 3 – 2 x 2 + 22 3 x – 8 ‘ , x > 0 y ‘ = – 1 2 x 2 – 4 x – 22 3 , x 0 1 2 x 2 – 4 x + 22 3 , x > 0

Точка х = 0 не имеет производной, потому как значения односторонних пределов разные. Получим, что:

lim y ‘ x → 0 – 0 = lim y x → 0 – 0 – 1 2 x 2 – 4 x – 22 3 = – 1 2 · ( 0 – 0 ) 2 – 4 · ( 0 – 0 ) – 22 3 = – 22 3 lim y ‘ x → 0 + 0 = lim y x → 0 – 0 1 2 x 2 – 4 x + 22 3 = 1 2 · ( 0 + 0 ) 2 – 4 · ( 0 + 0 ) + 22 3 = + 22 3

Отсюда следует, что функция непрерывна в точке х = 0 , тогда вычисляем

lim y x → 0 – 0 = lim x → 0 – 0 – 1 6 x 3 – 2 x 2 – 22 3 x – 8 = = – 1 6 · ( 0 – 0 ) 3 – 2 · ( 0 – 0 ) 2 – 22 3 · ( 0 – 0 ) – 8 = – 8 lim y x → 0 + 0 = lim x → 0 – 0 1 6 x 3 – 2 x 2 + 22 3 x – 8 = = 1 6 · ( 0 + 0 ) 3 – 2 · ( 0 + 0 ) 2 + 22 3 · ( 0 + 0 ) – 8 = – 8 y ( 0 ) = 1 6 x 3 – 2 x 2 + 22 3 x – 8 x = 0 = 1 6 · 0 3 – 2 · 0 2 + 22 3 · 0 – 8 = – 8

Необходимо произвести вычисления для нахождения значения аргумента, когда производная становится равной нулю:

– 1 2 x 2 – 4 x – 22 3 , x 0 D = ( – 4 ) 2 – 4 · – 1 2 · – 22 3 = 4 3 x 1 = 4 + 4 3 2 · – 1 2 = – 4 – 2 3 3 0 x 2 = 4 – 4 3 2 · – 1 2 = – 4 + 2 3 3 0

1 2 x 2 – 4 x + 22 3 , x > 0 D = ( – 4 ) 2 – 4 · 1 2 · 22 3 = 4 3 x 3 = 4 + 4 3 2 · 1 2 = 4 + 2 3 3 > 0 x 4 = 4 – 4 3 2 · 1 2 = 4 – 2 3 3 > 0

Все полученные точки нужно отметить на прямой для определения знака каждого интервала. Поэтому необходимо вычислить производную в произвольных точках у каждого интервала. Например, у нас можно взять точки со значениями x = – 6 , x = – 4 , x = – 1 , x = 1 , x = 4 , x = 6 . Получим, что

y ‘ ( – 6 ) = – 1 2 x 2 – 4 x – 22 3 x = – 6 = – 1 2 · – 6 2 – 4 · ( – 6 ) – 22 3 = – 4 3 0 y ‘ ( – 4 ) = – 1 2 x 2 – 4 x – 22 3 x = – 4 = – 1 2 · ( – 4 ) 2 – 4 · ( – 4 ) – 22 3 = 2 3 > 0 y ‘ ( – 1 ) = – 1 2 x 2 – 4 x – 22 3 x = – 1 = – 1 2 · ( – 1 ) 2 – 4 · ( – 1 ) – 22 3 = 23 6 0 y ‘ ( 1 ) = 1 2 x 2 – 4 x + 22 3 x = 1 = 1 2 · 1 2 – 4 · 1 + 22 3 = 23 6 > 0 y ‘ ( 4 ) = 1 2 x 2 – 4 x + 22 3 x = 4 = 1 2 · 4 2 – 4 · 4 + 22 3 = – 2 3 0 y ‘ ( 6 ) = 1 2 x 2 – 4 x + 22 3 x = 6 = 1 2 · 6 2 – 4 · 6 + 22 3 = 4 3 > 0

Изображение на прямой имеет вид

Значит, приходим к тому, что необходимо прибегнуть к первому признаку экстремума. Вычислим и получим, что

x = – 4 – 2 3 3 , x = 0 , x = 4 + 2 3 3 , тогда отсюда точки максимума имеют значени x = – 4 + 2 3 3 , x = 4 – 2 3 3

Перейдем к вычислению минимумов:

y m i n = y – 4 – 2 3 3 = 1 6 x 3 – 2 2 + 22 3 x – 8 x = – 4 – 2 3 3 = – 8 27 3 y m i n = y ( 0 ) = 1 6 x 3 – 2 2 + 22 3 x – 8 x = 0 = – 8 y m i n = y 4 + 2 3 3 = 1 6 x 3 – 2 2 + 22 3 x – 8 x = 4 + 2 3 3 = – 8 27 3

Произведем вычисления максимумов функции. Получим, что

y m a x = y – 4 + 2 3 3 = 1 6 x 3 – 2 2 + 22 3 x – 8 x = – 4 + 2 3 3 = 8 27 3 y m a x = y 4 – 2 3 3 = 1 6 x 3 – 2 2 + 22 3 x – 8 x = 4 – 2 3 3 = 8 27 3

Графическое изображение

y m i n = y – 4 – 2 3 3 = – 8 27 3 y m i n = y ( 0 ) = – 8 y m i n = y 4 + 2 3 3 = – 8 27 3 y m a x = y – 4 + 2 3 3 = 8 27 3 y m a x = y 4 – 2 3 3 = 8 27 3

Второй признак экстремума функции

Если задана функция f ‘ ( x 0 ) = 0 , тогда при ее f ” ( x 0 ) > 0 получаем, что x 0 является точкой минимума, если f ” ( x 0 ) 0 , то точкой максимума. Признак связан с нахождением производной в точке x 0 .

Найти максимумы и минимумы функции y = 8 x x + 1 .

Для начала находим область определения. Получаем, что

D ( y ) : x ≥ 0 x ≠ – 1 ⇔ x ≥ 0

Необходимо продифференцировать функцию, после чего получим

y ‘ = 8 x x + 1 ‘ = 8 · x ‘ · ( x + 1 ) – x · ( x + 1 ) ‘ ( x + 1 ) 2 = = 8 · 1 2 x · ( x + 1 ) – x · 1 ( x + 1 ) 2 = 4 · x + 1 – 2 x ( x + 1 ) 2 · x = 4 · – x + 1 ( x + 1 ) 2 · x

При х = 1 производная становится равной нулю, значит, точка является возможным экстремумом. Для уточнения необходимо найти вторую производную и вычислить значение при х = 1 . Получаем:

y ” = 4 · – x + 1 ( x + 1 ) 2 · x ‘ = = 4 · ( – x + 1 ) ‘ · ( x + 1 ) 2 · x – ( – x + 1 ) · x + 1 2 · x ‘ ( x + 1 ) 4 · x = = 4 · ( – 1 ) · ( x + 1 ) 2 · x – ( – x + 1 ) · x + 1 2 ‘ · x + ( x + 1 ) 2 · x ‘ ( x + 1 ) 4 · x = = 4 · – ( x + 1 ) 2 x – ( – x + 1 ) · 2 x + 1 ( x + 1 ) ‘ x + ( x + 1 ) 2 2 x ( x + 1 ) 4 · x = = – ( x + 1 ) 2 x – ( – x + 1 ) · x + 1 · 2 x + x + 1 2 x ( x + 1 ) 4 · x = = 2 · 3 x 2 – 6 x – 1 x + 1 3 · x 3 ⇒ y ” ( 1 ) = 2 · 3 · 1 2 – 6 · 1 – 1 ( 1 + 1 ) 3 · ( 1 ) 3 = 2 · – 4 8 = – 1 0

Значит, использовав 2 достаточное условие экстремума, получаем, что х = 1 является точкой максимума. Иначе запись имеет вид y m a x = y ( 1 ) = 8 1 1 + 1 = 4 .

Графическое изображение

Ответ: y m a x = y ( 1 ) = 4 ..

Третье достаточное условие экстремума

Функция y = f ( x ) имеет ее производную до n -го порядка в ε окрестности заданной точки x 0 и производную до n + 1 -го порядка в точке x 0 . Тогда f ‘ ( x 0 ) = f ” ( x 0 ) = f ‘ ‘ ‘ ( x 0 ) = . . . = f n ( x 0 ) = 0 .

Отсюда следует, что когда n является четным числом, то x 0 считается точкой перегиба, когда n является нечетным числом, то x 0 точка экстремума, причем f ( n + 1 ) ( x 0 ) > 0 , тогда x 0 является точкой минимума, f ( n + 1 ) ( x 0 ) 0 , тогда x 0 является точкой максимума.

Найти точки максимума и минимума функции y y = 1 16 ( x + 1 ) 3 ( x – 3 ) 4 .

Исходная функция – целая рациональная, отсюда следует, что область определения – все действительные числа. Необходимо продифференцировать функцию. Получим, что

y ‘ = 1 16 x + 1 3 ‘ ( x – 3 ) 4 + ( x + 1 ) 3 x – 3 4 ‘ = = 1 16 ( 3 ( x + 1 ) 2 ( x – 3 ) 4 + ( x + 1 ) 3 4 ( x – 3 ) 3 ) = = 1 16 ( x + 1 ) 2 ( x – 3 ) 3 ( 3 x – 9 + 4 x + 4 ) = 1 16 ( x + 1 ) 2 ( x – 3 ) 3 ( 7 x – 5 )

Данная производная обратится в ноль при x 1 = – 1 , x 2 = 5 7 , x 3 = 3 . То есть точки могут быть точками возможного экстремума. Необходимо применить третье достаточное условие экстремума. Нахождение второй производной позволяет в точности определить наличие максимума и минимума функции. Вычисление второй производной производится в точках ее возможного экстремума. Получаем, что

y ” = 1 16 x + 1 2 ( x – 3 ) 3 ( 7 x – 5 ) ‘ = 1 8 ( x + 1 ) ( x – 3 ) 2 ( 21 x 2 – 30 x – 3 ) y ” ( – 1 ) = 0 y ” 5 7 = – 36864 2401 0 y ” ( 3 ) = 0

Значит, что x 2 = 5 7 является точкой максимума. Применив 3 достаточный признак, получаем, что при n = 1 и f ( n + 1 ) 5 7 0 .

Необходимо определить характер точек x 1 = – 1 , x 3 = 3 . Для этого необходимо найти третью производную, вычислить значения в этих точках. Получаем, что

y ‘ ‘ ‘ = 1 8 ( x + 1 ) ( x – 3 ) 2 ( 21 x 2 – 30 x – 3 ) ‘ = = 1 8 ( x – 3 ) ( 105 x 3 – 225 x 2 – 45 x + 93 ) y ‘ ‘ ‘ ( – 1 ) = 96 ≠ 0 y ‘ ‘ ‘ ( 3 ) = 0

Значит, x 1 = – 1 является точкой перегиба функции, так как при n = 2 и f ( n + 1 ) ( – 1 ) ≠ 0 . Необходимо исследовать точку x 3 = 3 . Для этого находим 4 производную и производим вычисления в этой точке:

y ( 4 ) = 1 8 ( x – 3 ) ( 105 x 3 – 225 x 2 – 45 x + 93 ) ‘ = = 1 2 ( 105 x 3 – 405 x 2 + 315 x + 57 ) y ( 4 ) ( 3 ) = 96 > 0

Из выше решенного делаем вывод, что x 3 = 3 является точкой минимума функции.

Графическое изображение

Ответ: x 2 = 5 7 является точкой максимума, x 3 = 3 – точкой минимума заданной функции.

Возрастание и убывание функции

Общие понятия о поведении функций

Исследуя функции, заданные определенными уравнениями, особенно уделяют внимание их свойствам, а именно возрастанию или убыванию.

Монотонной функцией называется функция, меняющаяся в одном направлении.
На графиках представлены примеры монотонно возрастающей и монотонно убывающей функций.

Соответственно, монотонная функция может быть возрастающая или убывающая.

Возрастающей называется такая функция, у которой при увеличении значения аргумента, значение функции увеличивается, иными словами, чем больше значение аргумента, тем больше значение функции.

Математическое выражение этого определения выглядит следующим образом:

Убывающей называется такая функция, у которой при увеличении значения аргумента, значение функции уменьшается, иными словами, чем больше значение аргумента, тем меньшее значение функции.

Математическое выражение этого определения выглядит следующим образом:

Разберем примеры решения задач на изучение характера поведения функции.

Задача 1. Задана функция (y=x^3+1) . Исследовать ее характер в интервале ([0;2]) .
Решение: Подставим поочередно крайние значения заданного отрезка и сравним полученные значения функции.
(y_1=0^3+1=1) ;
(y_2=2^3+1=9) .

Поскольку значения функции увеличиваются, при увеличении значений аргумента, то данная функция на заданном отрезке будет возрастать.

Задача 2 . Задана функция (y=<1over x>) . Определить ее характер в интервале ([1;2]) .
Решение: Подставим поочередно крайние значения заданного отрезка и сравним полученные значения функции.
(y_1=<1over 1>=1) ;
(y_2=<1over2>=0.5) .

Поскольку значения функции уменьшаются, при увеличении значений аргумента, то данная функция на данном отрезке будет убывать.

Не возрастающей называется такая функция, у которой при увеличении значения аргумента, значение функции увеличивается или остается на том же уровне, иными словами, большему значению аргумента соответствует большее или равное значение функции.

Не нашли что искали?

Просто напиши и мы поможем

Не убывающей называется такая функция, у которой при увеличении значения аргумента, значение функции уменьшается или остается на том же уровне, иными словами, большему значению аргумента соответствует меньшее или равное значение функции.

Постоянной называется такая функция, которая не убывает и не возрастает, то есть при увеличении или при уменьшении значения аргумента, значение функции остается на одном и том же уровне. Пример такой функции можно наблюдать на рисунке.

Разберем задачу на исследование характера поведения функции. При данной функции (y=5) исследовать ее характер в интервале ([0;2]) .

По сути эту функцию можно записать как (y=5+0∙x) , подставляя крайние значения отрезка, получим:
(y_1=5+0∙0=5) ;
(y_2=5+0∙2=5) .

То есть функция (y=5) будет постоянной.

Постоянная, не убывающая и не возрастающая функции не есть монотонные.

Свойства монотонных функций

К свойствам монотонных функций относятся такие характеристики:

• если две или больше возрастающих функций суммируются, то в результате получается тоже возрастающая функция;
• результатом произведения положительных возрастающих функций будет возрастающая функция;
• при композиции двух возрастающих функций получается также функция, которая будет возрастать;
• при положительной функции (f(x)) , функция (f^n (x)) тоже будет возрастать, при условии, что (n) является натуральным числом;
• при сохранении возрастающей функцией (f(x)) своего знака, обратная ей функция будет убывать;
• при возрастающей функции (f(x)) и константе c справедливо, что функции (cf(x)) и (f(x)+c) , при (c>0) , будут возрастать.

Монотонность производной и заданной функций связаны между собой, и это описано в таких теоремах:

Возрастание и убывание функции

Вы будете перенаправлены на Автор24

При исследовании заданной функции особое внимание уделяется характеру ее поведения: возрастает, не возрастает, убывает, не убывает.

Монотонная функция — это функция, которая меняется в одном и том же направлении.

Примеры монотонных функций приведены на рисунках:

Рисунок 1. Возрастающая функция

Рисунок 2. Убывающая функция

Монотонные функции делят на:

• убывающие функции;
• возрастающие функции.

Функция является возрастающей, если для большего значения аргумента соответствует большее значение заданной функции. Другими словами, если при возрастании значений аргумента значения заданной функции тоже возрастают, то заданная функция возрастает.

Математическая запись определения 2: $f(x):uparrow x_

Функция является убывающей, если для большего значения аргумента соответствует меньшее значение заданной функции. Другими словами, если при возрастании значений аргумента значения заданной функции убывают, то заданная функция убывает.

Математическая запись определения 3: $f(x):downarrow x_ <1>f(x_<2>)$.

Определить характер функции $y=x^ <3>+1$ на отрезке $[0;2]$

Следовательно, заданная функция возрастает на заданном отрезке $[0;2]$.

Готовые работы на аналогичную тему

Определить характер функции $y=frac<1> $ на отрезке $[1;2]$

Следовательно, заданная функция убывает на заданном отрезке $[1;2]$.

Функция является не возрастающей, если для большего значения аргумента соответствует большее или равное значение заданной функции.

Математическая запись определения 4: $f(x): x_

Функция является не убывающей, если для большего значения аргумента соответствует меньшее или равное значение заданной функции.

Математическая запись определения 5: $f(x):x_

Постоянная функция — это функция, которая не возрастает и не убывает.

Математическая запись определения 6: $f(x):x_

Определить характер функции $y=5$ на отрезке $[0;2]$

Следовательно, заданная функция постоянна на заданном отрезке $[0;2]$.

Не возрастающая, не убывающая и постоянная функции не являются монотонными.

Монотонные функции обладают следующими свойствами:

• сумма двух и более возрастающих функций есть возрастающая функция;
• произведение неотрицательных возрастающих функций является возрастающей функцией;
• если возрастающая функция $f(x)$ сохраняет свой знак, то обратная функция $1/f(x)$ является убывающей;
• если возрастающая функция $f(x)$ неотрицательна, то функция $f^ (x)$ также является возрастающей (n — натуральное число);
• для возрастающей функции $f(x)$ и константы $c$ имеем, что функции $cf(x)$, где $c>0$, и $f(x)+c$ возрастают, а функция $cf(x)$, где $c
• Композиция двух возрастающих функций является возрастающей функцией.

Между монотонностью заданной функции и ее производной существует определенная связь, которая описывается следующими теоремами:

Если производная $f'(x)$ заданной функции положительная на некотором промежутке, то данная функция возрастает на рассматриваемом промежутке.

Если производная $f'(x)$ заданной функции отрицательна на некотором промежутке, то данная функция убывает на рассматриваемом промежутке.

Сформулируем обратные теоремы.

Теорема, обратная к теореме 1.

Если заданная функция является возрастающей на некотором промежутке, то производная данной функции неотрицательна или не существует.

Теорема, обратная к теореме 2.

Если заданная функция является убывающей на некотором промежутке, то производная данной функции неположительная или не существует.

Для постоянной функции имеет место следующая теорема:

Функция $y=f(x)$ является постоянной на некотором промежутке, если ее производная равна нулю для всех точек из этого промежутка.

Алгоритм исследования функции на возрастание и убывание включает следующие этапы:

• нахождение производной заданной функции;
• нахождение стационарных и критических точек ($f'(x)=0$ или не существует);
• определение знака производной на каждом промежутке;
• определение характера поведения функции на каждом промежутке.

Определить характер функции $y=frac $ на интервале $(-infty ;+infty )$

1. Производная функции: $y’=left(fracright)’=frac<1cdot (x-2)-xcdot 1><(x-2)^<2>> =frac<(x-2)^<2>> =-frac<2><(x-2)^<2>> $
2. Производная неопределенна при $x=2$. Стационарных точек нет.
3. Исследуем знак производной с помощью числовой прямой.

[y'(0)=-frac<2><(0-2)^<2>> =-frac<2><4>=-frac<1><2>
Определим характер поведения функции.

Следовательно, заданная функция убывает на всей области определения

Определить характер функции $y=x^ <3>-12x$ на интервале $(-infty ;+infty )$

1. Производная функции: $y’=left(x^ <3>-12xright)’=3x^ <2>-12$
2. Производная определенна на всем интервале. [y’=0;, , , 3x^ <2>-12=0Rightarrow 3x^ <2>=12to x^ <2>=4Rightarrow x=pm 2]

$x=pm 2$ – стационарные точки

1. Исследуем знак производной с помощью числовой прямой.

[y'(0)=3cdot 0^ <2>-12=-120]

1. Определим характер поведения функции.

Следовательно, заданная функция убывает на $[-2;2]$, возрастает на $(-infty ;-2]$ и $[2;+infty )$.

Возрастание, убывание и монотонность функции

Понятие возрастания, убывания и монотонности функции

Исследование функции на возрастание и убывание может быть как самостоятельной задачей, так и одним из этапов полного исследования функции и построения её графика.

Функции, у которых имеет место убывание или возрастание на некотором числовом промежутке, называются монотонными функциями.

Возрастание функции. Функция называется возрастающей на интервале ]a, b[ , принадлежащем области определения функции, если бОльшим значениям независимой переменной из этого интервала соответствуют бОльшие значения функции, т.е. если

x 2 > x 1 → f(x 2 ) > f(x 1 ) для всех x 1 и x 2 , принадлежащих интервалу. Кстати, будет полезным открыть в новом окне материал Свойства и графики элементарных функций.

Убывание функции. Функция называется убывающей на интервале ]a, b[ , если бОльшим значениям независимой переменной из этого интервала соответствуют меньшие значения функции, т.е. если

x 2 > x 1 → f(x 2 ) 1 ) для всех x 1 и x 2 , принадлежащих интервалу.

Признаки постоянства, возрастания и убывания функции

Теорема 1. Если во всех точках некоторого промежутка производная функции равна нулю ( f ‘(x) = 0 ), то функция f(x) сохраняет в этом промежутке постоянное значение.

Этот промежуток может быть замкнутым или открытым, конечным или бесконечным.

Теорема 2 (достаточный признак возрастания). Если во всех точках некоторого промежутка производная функции больше нуля ( f ‘(x) > 0 ), то функция f(x) возрастает в этом промежутке.

Теорема 3 (достаточный признак убывания). Если во всех точках некоторого промежутка производная функции меньше нуля ( f ‘(x) ), то функция f(x) убывает на этом промежутке.

Замечание. Условия теорем 2 и 3 не являются в полной мере необходимыми. Их можно несколько ослабить, а именно заменить нестрогими неравенствами и считать, что производная функции больше или равна нулю ( f ‘(x) ≥ 0 ) или меньше или равна нулю ( f ‘(x) ≤ 0 ), так как заключения теорем остаются справедливыми и тогда, когда производная обращается в нуль в конечном множестве точек.

Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.

Пример 1. Найти промежутки возрастания и убывания функции

Решение. Находим производную функции:

(Для разложения квадратного двухчлена на множители решали квадратное уравнение).

Для отыкания промежутков возрастания и убывания функции найдём точки, в которых . Такими точками являются и .

Исследуем знаки производной в промежутках, ограниченных этими точками. От до точки знак положителен, от точки до точки знак отрицателен, от точки до знак положителен. Ответ на вопрос задания: промежутки возрастания данной функции – и , а промежуток убывания функции – .

Пример 2. Найти промежутки возрастания и убывания функции .

Решение. Находим производную функции:

Решая уравнение , получаем точки, в которых производная функции равна нулю:

.

Исследуем знаки производной. От до точки знак положителен, от точки до точки знак отрицателен, от точки до знак положителен. Наше исследование показало, что промежутки возрастания данной функции и , а промежуток убывания –

Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.

Пример 3. Найти промежутки возрастания и убывания функции .

Решение. Область определения функции – промежуток , так как логарифмическая функция определена при .

Далее находим производную функции:

.

Решая уравнение , получаем точку, в которой производная равна нулю:

Исследуем знаки производной. От 0 до точки знак отрицателен, от точки до знак положителен. Ответ: промежуток убывания функции – , а промежуток возрастания – .