Линейная функция, ее свойства и график

теория по математике функции

Функция, заданная формулой y=kx+b, где х – переменная, k и b – некоторые числа, называется линейной функцией. Переменную х называют независимой переменной, переменную у – зависимой переменной.

Графиком линейной функции является прямая. Для построения прямой достаточно взять два значения х, чтобы получить два значения у и, соответственно, две точки, через которые проходит единственная прямая.

Число k называется угловым коэффициентом прямой.

Свойства линейной функции

Область определения функции – множество всех действительных чисел. То есть в данную формулу мы можем подставлять любое значение х.
Областью значений также является множество всех действительных чисел.
Функция не имеет ни наибольших, ни наименьших значений.
При k – положительном, угол наклона к оси х острый, другими словами – график функции возрастает.
При k отрицательном угол наклона к оси х тупой, то есть график функции – убывает.
При k=0 прямая параллельна оси х.
Частный случай линейной функции: y=kx, где число b=0, эту функцию называют прямой пропорциональностью, график такой функции проходит через начало координат.

Рассмотрим на примерах расположение прямых в координатной плоскости в зависимости от значения чисел k и b.

Пример №1

Построить график функции у=2х – 1. Для того, чтобы удобнее было выполнять вычисления, построение и т.д. сделаем таблицу для значений х и у:

Для построения графика подбираем два значения х, одно из них желательно брать равное нулю, второе, например 3 (подбираем небольшие числа).

х		3
у

Теперь подставляем значения х в формулу и вычисляем соответствующие значения у:

у=2х – 1=2 × 0 – 1= –1;

у=2х – 1=2 × 3 – 1= 5.

Вписываем в таблицу значения у:

х		3
у	–1	5

Теперь строим систему координат, отмечаем в ней точки с координатами А(0; –1) и В(3;5), проводим через эти две точки прямую.

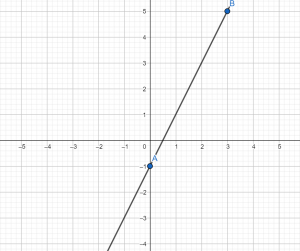
Итак, по формуле мы видим, что угловой коэффициент — положительный, значит, график – возрастает, что мы и видим на нашем графике.

Пример №2.

Построить график функции у= –3х+4. Итак, делаем таблицу на два значения, например, возьмем 0 и 2.

х		2
у	4	–2

По формуле видим, что угловой коэффициент отрицательный, значит, прямая будет убывать. Строим убывающую прямую в системе координат через две точки А(0;4) и В(2; –2).

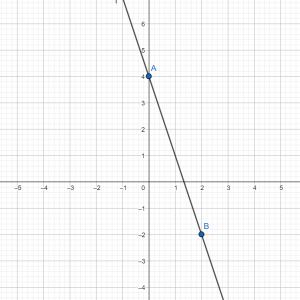
Пример №3

Построить график функции у=4. Видим, что в данном случае число х=0, значит, прямая будет проходить через точку с координатой (0;4) параллельно оси х. На графике это выглядит следующим образом:

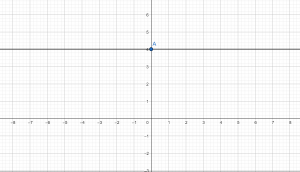
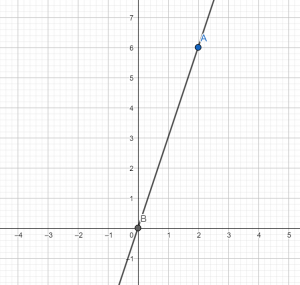
Построить график функции у=3х. Данная функция является частным случаем, когда прямая проходит через начало координат. Поэтому в данном случае можно взять устно одно значение х, например 2, тогда у получим равный 6. Таким образом, имеем две точки (2;6) и (0;0). Строим их в системе координат и проводим через них прямую, которая будет возрастать, так как угловой коэффициент равен 3, т.е. положительный.

На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.

ассмотрим коэффициенты под №3. Если k 90 0 ) угол с положит.направлением оси абсцисс (Ох). Если b 0. Это соответствует оставшимся графикам А и Б, т.к. они оба наклонены к положительно направлению оси Оx под острым углом ( 0 ). Следовательно, выбор соответствия должен быть выполнен по коэффициенту b.

Что такое линейная функция: определение, формула, график

В данной публикации мы рассмотрим, что такое линейная функция, а также приведем ее формулу и график. Представленная информация сопровождается практическими примерами для лучшего понимания.

Определение линейной функции
График линейной функции

Определение линейной функции

Линейная функция – это функция, которая имеет вид .

x – независимая переменная (аргумент);
a и b – произвольные числа.

Подставляя в эту формулу конкретные значения x, мы можем рассчитать соответствующие им значения y.

Пример: дана функция y = 2x – 3. Составим для нее таблицу соответствия x и y.

” data-lang=”default” data-override=”<"emptyTable":"","info":"","infoEmpty":"","infoFiltered":"","lengthMenu":"","search":"","zeroRecords":"","exportLabel":"","file":"default">” data-merged=”[]” data-responsive-mode=”2″ data-from-history=”0″>

	-3	2 ⋅ 0 – 3 = -3
1	-1	2 ⋅ 1 – 3 = -1
2	1	2 ⋅ 2 – 3 = 1
3	3	2 ⋅ 3 – 3 = 3

График линейной функции

Графиком линейной функции y = ax + b является непрерывная прямая линия. При этом она может быть:

возрастающей при a > 0 (значение y монотонно увеличивается);
убывающей при a

Линейная функция.

Линейной функцией называется функция, заданная формулой y = kx + b , где k и b – любые действительные числа.
Графиком линейной функции является прямая.

Если k = 0, то функция y = b называется постоянной. Её графиком, является прямая, параллельная оси Ox.
Если b = 0, то формула y = kx задает прямо пропорциональную зависимость. Графиком такой функции является прямая, проходящая через начало координат.

Верно и обратное – любая прямая, не параллельная оси Oy, является графиком некоторой линейной функции.

Построить график линейной функции очень легко.
Положение любой прямой однозначно определяется заданием двух её точек. Поэтому линейная функция вполне определяется заданием её значений для двух значений аргумента. Например,

x 1

y b k + b

Если Вы являетесь моим учеником или подписчиком, то можете поработать с интерактивными версиями этих графиков.

Свойства линейной функции при k ≠ 0, b ≠ 0.
1) Область определения функции – множество всех действительных чисел: R или (−∞; ∞).
2) Функция y = kx + b ни четна, ни нечетна.
3) При k > 0 функция монотонно возрастает, а при k Упражнение:
На рисунке представлены 4 прямые линии. Могут ли они являться графиками функций? Если да, то определите каких.

Прямые, наклоненные к оси абсцисс под острым или тупым углом – графики линейной функции общего вида: y = kx + b. Параметр b легко определить по точке пересечения линии с осью ординат (Oy). Параметр k определяется построеним по клеточкам треугольника, содержащего угол α для острых углов или смежный с ним – для тупых. Точные ответы на рисунке.
Прямая, параллельная оси абсцисс (здесь – горизонтальная линия), является графиком частного вида линейной функции y = b, который называют постоянной или константой. Значение этой функции не изменяется, поэтому ординаты точки графика всегда находятся на одной высоте относительно оси Ox.

Следующая прямая линия НЕ является графиком какой-либо функции. Здесь нет однозначности. Если x = 6, то y = ? Любому действительному числу! Т.е., для неё не удовлетворяется определение функции, а именно условие, что каждому значению аргумента x должно соответствовать единственное значение функции y. Но такие линии нам тоже встречаются, например, в качестве вертикальных асимптот. Поэтому нужно знать, что их уравнение x = a, где а – заданное число.

Видеоуроки для подготовки к ОГЭ по математике. 9 класс.

Подробное исследование коэффициентов линейной функции.

Примеры решения заданий ОГЭ по математике.

Понравились материалы сайта? Узнайте, как поддержать сайт и помочь его развитию.

Есть вопросы? пожелания? замечания? Обращайтесь – mathematichka@yandex.ru

Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено.

Линейная функция. Прямая пропорциональность

Содержание

Из прошлого урока вы узнали многое о функциях, но далеко не все. Вспомним основные знания, которые нам будут нужны для понимания линейной функции:

функция – это зависимость между двумя величинами, при которой каждому значению независимой переменной $x$ соответствует одно единственное значение другой зависимой переменной $y$;

зависимость может быть прямой и обратной

любая функция имеет область определения и область значений;

графически функция может убывать и/или возрастать, может выглядеть как прямой, так и кривой линией.

Вот о функциях, график которых выглядит как прямая линия, и пойдет речь в данном уроке.

Примеры линейных функций

Представим ситуацию: в копилке лежит $500$ рублей, мама дает дочке каждый день на обеды и другие мелкие расходы $100$ рублей, но она тратит только $50$, а $50$ рублей кладет в копилку. Таким образом, через $10$ дней в копилке девочки будет уже на $500$ рублей больше: $50times 10$. Всего же в копилке через $10$ дней будет $1000$ рублей: $500$ рублей накоплено за эти $10$ дней и $500$ рублей уже было.

Посмотрим, сколько же будет в копилке через $20$ дней: $ <50times 20>+ 500 = 1500$ рублей.

Возьмем за функцию (зависимую переменную $y$) общее количество денег в копилке. Число дней, когда откладывались деньги, обозначим за $x$ (независимая переменная). Тогда наша функция (зависимость количества денег в копилке от количества прошедших дней) будет выглядеть в виде формулы: $y = <50times x>+ 500$.

Посмотрим, как будет выглядеть график нашей функции. Для этого найдем несколько значений $y$ и заполним таблицу для $x$, например, равных $4$, $5$, $6$, $7$ (дней):

Найдем $y_1 = <50times 4>+ 500 = 700$

Тогда $y_2 = <50times 5>+ 500 = 750$

$x$ $4$ $5$ $6$ $7$

$y$ $700$ $750$ $800$ $850$

По точкам с координатами $(4, 700)$; $(5, 750)$; $(6, 800)$ и $(7, 850)$ построим график:

Как видим, график функции $y = <50times x>+ 500$ выглядит как прямая линия.

Таким образом, увеличение денег в копилке будет напрямую зависеть от количества дней, в которые она пополнялась на одну и ту же сумму. При этом, зависимая переменная $y$ меняется на одну и ту же величину (в нашем случае ежедневное приращение суммы равно $50$ рублям).

Другой пример. Летом отключили горячую воду. Водонагреватель сломался, а помыться нужно. В ванну сначала налили два ведра кипятка, каждое по $10$ литров. Затем в нее пустили холодную воду из крана. В течение каждой минуты в ванну добавлялось еще 5 литров воды. Зависимость количества воды в ванной в нашем случае можно выразить с помощью формулы $y = <5times x>+ 20$, где $y$ – количество воды в ванной, а $x$ – время в минутах, которое прошло с момента включения крана.

Что такое линейная функция

Итак, зависимость, подобная нашим примерам выше, функцию которой можно найти с помощью формулы вида $y = kx + b$, и называется линейной.

В данной формуле $k$ и $b$ – некоторые числа, называемые коэффициентами.

В наших случаях коэффициент $k$ был равен $50$ в примере с копилкой и $5$ в примере с ванной. Коэффициент $b$ в описанных примерах был равен $500$ рублям, уже лежавшим в копилке, и $20$ литрам, налитым в ванну до включения крана.

Если функцию можно задать формулой вида $y = kx + b$, где $k$ и $b$ – некоторые числа, а $x$ – независимая переменная, то ее называют линейной

Числовые коэффициенты $k$ и $b$ могут быть любыми числами: дробными и даже отрицательными.

Прямая пропорциональность и другие особые случаи

Давайте посмотрим, какие функции также будут линейными:

$y = -3times x- b$, в данном случае оба числовых коэффициента имеют отрицательные значения;

другой пример: $y = 2-x$, здесь коэффициент $k$ равен $-1$, а $b = 2$;

$y = 5$, тут коэффициент $k$ равен $0$, а коэффициент $b=5$ (в подобных случаях функция совсем не зависит от значения аргумента $x$, а лишь от числовой величины коэффициента $b$);

а в функции $y = 4times x$ коэффициент $b$ уже равен $0$.

Последний пример линейной функции (когда коэффициент $b$ равен $0$) – вариант прямой пропорциональности. Ранее вы уже изучали прямую зависимость. Такая зависимость – частный случай линейной функции, при котором формула будет выглядеть, как $y = kx$.

Вспомнить, что такое прямая зависимость

Если при увеличении одной величины, увеличивается другая, то величины называют прямо пропорциональными, у них прямая зависимость.

Чем больше денег – тем больше можно купить мороженого

Вернемся снова к нашим примерам: если бы в копилке и в ванной изначально было пусто, то функция $y$ увеличивалась бы прямо пропорционально увеличению количества потраченного на наполнение копилки или ванны времени. Коэффициент $b$ в таких случаях равен нулю.

Обратите внимание, что в формуле прямо пропорциональной функции коэффициент $b = 0$, но коэффициент $k$ не равен нулю.

Линейная функция (ЕГЭ 2022)

Зависимость одной величины от другой математики называют функций одной величины от другой.

Количество денег — это функция вашей зарплаты (иногда говорят «от зарплаты»).

Вес — это функция от съеденных круассанов. Чем меньше съел, тем меньше весишь.

Расстояние — это функция времени. Чем дольше ты будешь идти, тем больше пройдешь.

Ну а теперь перейдем к одному из видов функций – линейной функции.

Линейная функция — коротко о главном

Линейная функция –это функция вида ( y=kx+b), где ( k) и ( b) – любые числа (коэффициенты).

Рассмотрим, как коэффициенты влияют на месторасположение графика:

( k) — отвечает за угол наклона графика (( displaystyle k=tgalpha ))

( displaystyle b) — точка пересечения с ( displaystyle Oy)

Общие варианты представлены на рисунке:

Линейная функция

Но сначала официальное определение «Функции» – теперь ты его поймешь. Держи в уме: деньги – зарплата, вес – круассаны, расстояние – время.

Функция – это правило, по которому каждому элементу одного множества (аргументу) ставится в соответствие некоторый (единственный!) элемент другого множества (множества значений функции).

То есть, если у тебя есть функция ( y=fleft( x right)), это значит что каждому допустимому значению переменной ( x) (которую называют «аргументом») соответствует одно значение переменной ( y) (называемой «функцией»).

Что значит «допустимому»?

Все дело в понятии «область определения»: для некоторых функций не все аргументы «одинаково полезны» — не все можно подставить в зависимость.

Например, для функции ( y=sqrt) отрицательные значения аргумента ( x) – недопустимы.

Ну и вернемся, наконец, к теме данной статьи.

Линейной называется функция вида ( y=kx+b), где ( k) и ( b) – любые числа (они называются коэффициентами).

Другими словами, линейная функция – это такая зависимость, что функция прямо пропорциональна аргументу.

Как думаешь, почему она называется линейной?

Все просто: потому что графиком этой функции является прямая линия. Но об этом чуть позже.

Как уже говорилось в теме «Функции», важнейшими понятиями, связанными с любой функцией, являются ее область определения ( Dleft( y right)) и область значений ( Eleft( y right)).

Область определения линейной функции

Какими могут быть значения аргумента линейной функции ( y=kx+b)? Правильно, любыми. Это значит, что область определения – все действительные числа:

( Dleft( y right)=mathbb)

или ( Dleft( y right)=left( -infty ;+infty right)).

А множество значений?

Область значений линейной функции

Тут тоже все просто: поскольку функция прямо пропорциональна аргументу, то чем больше аргумент ( x), тем больше значение функции ( y).

Значит, ( y) так же как и ( x) может принимать все возможные значения, то есть ( Eleft( y right)=mathbb), верно?

Верно, да не всегда. Есть такие линейные функции, которые не могут принимать любые значения. Как думаешь, в каком случае возникают ограничения?

Вспомним формулу: ( y=kx+b). Какие нужно выбрать коэффициенты ( k) и ( b), чтобы значение функции y не зависело от аргумента ( x)?

А вот какие: ( b) – любое, но ( k=0). И правда, каким бы ни был аргумент ( x), при умножении на ( k=0) получится ( 0)!

Тогда функция станет равна ( y=0cdot x+b=b), то есть она принимает одно и то же значение при всех ( x):

( y = kx + b:>left[ beginEleft( y right) = mathbb>k ne 0\Eleft( y right) = left< b right>>k = 0.end right.)

Теперь рассмотрим несколько задач на линейную функцию.

Три задачи на линейную функцию

При увеличении аргумента функции ( y=kx+b) на ( 2), функция увеличилась на ( 4). Найдите коэффициент ( k).

При увеличении аргумента функции ( y=kx+b) на ( 1), функция уменьшилась на ( 3). Найдите коэффициент ( k).

Дана функция ( y=kx+b). При ( x=3:y=1), а при ( x=5:y=-1). Определите коэффициенты ( k) и ( b) функции.

Решение задачи №1

Пусть начальное значение аргумента равно некому числу ( <_<1>>). После увеличения на ( 2) аргумент стал равен: ( <_<2>>=<_<1>>+2).

Чему была равна функция до увеличения? Подставляем аргумент в формулу:

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Решение задачи №2

Аналогично предыдущей задаче:

Начальное значение аргумента равно ( <_<1>>), конечное – ( <_<2>>=<_<1>>+1).

Начальное значение функции: ( <_<1>>=k<_<1>>+b);

В этот раз функция не увеличилась, а уменьшилась. Это значит, что конечное значение будет меньше начального, а значит, изменение (разность конечного и начального) будет отрицательным:

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Определение прямой пропорциональной зависимости

Если проанализировать решения этих двух задач, можно прийти к важному выводу.

При изменении аргумента линейной функции на ( Delta x) функция изменяется на ( kcdot Delta x). То есть изменение функции всегда ровно в ( mathbf) раз больше изменения аргумента.

По сути это является определением прямой пропорциональной зависимости.

Решение задачи №3

Подставим известные значения аргумента и функции в формулу ( y=kx+b):

Получили два уравнения относительно ( k) и ( b). Теперь достаточно решить систему этих двух уравнений:

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

График линейной функции

Как я уже упоминал ранее, график такой функции – прямая линия.

Как известно из геометрии, прямую можно провести через две точки (то есть, если известны две точки, принадлежащие прямой, этого достаточно, чтобы ее начертить).

Предположим, у нас есть функция линейная функция ( y=2x+1). Чтобы построить ее график, нужно вычислить координаты любых двух точек.

То есть нужно взять любые два значения аргумента ( x) и вычислить соответствующие два значения функции.

Затем для каждой пары ( left( x;y right)) найдем точку в системе координат, и проведем прямую через эти две точки.

Проще всего найти функцию, если аргумент ( x=0:yleft( 0 right)=2cdot 0+1=1).

Итак, первая точка имеет координаты ( left( 0;1 right)).

Теперь возьмем любое другое число в качестве ( x), например, ( x=1:yleft( 1 right)=2cdot 1+1=3).

Вторая точка имеет координаты ( left( 1;3 right)).

Ставим эти две точки на координатной плоскости:

Теперь прикладываем линейку, и проводим прямую через эти две точки:

Вот и все, график построен!

Давай теперь на этом же рисунке построим еще два графика: ( y= -1) и ( y=-x+2).

Построй их самостоятельно так же: посчитай значение y для любых двух значений ( x), отметь эти точки на рисунке и проведи через них прямую.

Должно получиться так:

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Видно, что все три прямые по-разному наклонены и в разных точках пересекают координатные оси. Все дело тут в коэффициентах ( displaystyle k) и ( displaystyle b).

Давай разберемся, на что они влияют.

Коэффициенты линейной функции

Для начала выясним, что делает коэффициент ( displaystyle b). Рассмотрим функцию ( displaystyle y=x+b), то есть ( displaystyle k=1).

Меняя ( displaystyle b) будем следить, что происходит с графиком.

Итак, начертим графики для разных значений ( displaystyle b_b=-2,text< ->1,text< >0,text< >1,text< >2):

Что ты можешь сказать о них? Чем отличаются графики?

Это сразу видно: чем больше ( displaystyle b), тем выше располагается прямая.

Более того, заметь такую вещь: график пересекает ось ( displaystyle mathbf) в точке с координатой, равной ( displaystyle mathbf)!

И правда. Как найти точку пересечения графика с осью ( displaystyle y)? Чему равен ( displaystyle x) в такой точке?

В любой точке оси ординат (это название оси ( displaystyle y), если ты забыл) ( displaystyle x=0).

Значит достаточно подставить ( displaystyle x=0) в функцию, и получим ординату пересечения графика с осью ( displaystyle y):

( displaystyle y=kcdot 0+b=b)

Теперь по поводу ( displaystyle k). Рассмотрим функцию ( displaystyle left( b=0 right).) Будем менять ( displaystyle k) и смотреть, что происходит с графиком.

Построим графики для ( displaystyle k=-3,text< ->1,text< >0,text< >1,text< >2:)

Так, теперь ясно: ( displaystyle k) влияет на наклон графика.

Чем больше ( displaystyle k) по модулю (то есть несмотря на знак), тем «круче» (под большим углом к оси абсцисс – ( displaystyle Ox)) расположена прямая.

Если ( displaystyle k>0), график наклонен «вправо», при ( displaystyle k

Выберем на графике две точки ( displaystyle A) и ( displaystyle B). Для простоты выберем точку ( displaystyle A) на пересечении графика с осью ординат. Точка ( displaystyle B) – в произвольном месте прямой, пусть ее координаты равны ( displaystyle left( x;y right)).

Рассмотрим прямоугольный треугольник ( displaystyle ABC), построенный на отрезке ( displaystyle AB) как на гипотенузе.

Из рисунка видно, что ( displaystyle AC=x), ( displaystyle BC=y-b).

Подставим ( displaystyle y=kx+b) в ( displaystyle BC_BC=y-b=kx+b-b=kx).

Получается, что ( BC = k cdot AC> Rightarrow >k = frac<><> = nolimits> alpha ).

Итак, коэффициент ( displaystyle k) равен тангенсу угла наклона графика, то есть угла между графиком и осью абсциссс.

Именно поэтому его (коэффициент ( displaystyle k)) обычно называют угловым коэффициентом.

В случае, когда ( k

Если же ( displaystyle k=0), тогда и ( nolimits> alpha = 0,) следовательно ( displaystyle alpha =0), то есть прямая параллельна оси абсцисс.

Понимать геометрическое значение коэффициентов очень важно, оно часто используется в различных задачах на линейную функцию.

Разбор еще трех задач на линейную функцию

1. Найдите коэффициенты ( displaystyle k) и ( displaystyle b) линейной функции, график которой приведен на рисунке. Запишите уравнение этой функции.

2. Найдите коэффициенты ( displaystyle k) и ( displaystyle b) линейной функции, график которой приведен на рисунке. Запишите уравнение этой функции.

3. График какой из функций изображен на рисунке?

Решение задачи №1

Коэффициент ( b) найти проще простого – это ведь точка пересечения графика с осью ( displaystyle Oy):

Угловой коэффициент ( displaystyle k) – это тангенс угла наклона прямой.

Для его нахождения выберем две точки ( displaystyle A) и ( displaystyle B) на графике и построим прямоугольный треугольник с гипотенузой ( displaystyle AB):

Линейная функция « y = kx + b » и её график

Прежде чем перейти к изучению функции « y = kx » внимательно изучите урок
«Что такое функция в математике» и «Как решать задачи на функцию».

Функцию вида « y = kx + b » называют линейной функцией.

Буквенные множители « k » и « b » называют числовыми коэффициентами .

Вместо « k » и « b » могут стоять любые числа (положительные, отрицательные или дроби).

Другими словами, можно сказать, что « y = kx + b » — это семейство всевозможных функций, где вместо « k » и « b » стоят числа.

Примеры функций типа « y = kx + b ».

y = 5x + 3

y = −x + 1

y =

2

3

x − 2

y = 0,5x

Давайте определим для каждой функций выше, чему равны числовые коэффициенты « k » и « b » .

Обратите особое внимание на функцию « y = 0,5x » в таблице. Часто совершают ошибку при поиске в ней числового коэффициента « b ».

Рассматривая функцию « y = 0,5x », неверно утверждать, что числового коэффициента « b » в функции нет.

Числовый коэффициент « b » присутствет в функции типа « y = kx + b » всегда. В функции « y = 0,5x » числовый коэффициент « b » равен нулю .

Как построить график линейной функции
« y = kx + b »

Графиком линейной функции « y = kx + b » является прямая .
Так как графиком функции « y = kx + b » является прямая линия , функцию называют линейной функцией.

Из геометрии вспомним аксиому (утверждение, которое не требует доказательств), что через любые две точки можно провести прямую и притом только одну.

Исходя из аксиомы выше следует, что чтобы построить график функции вида
« у = kx + b » нам достаточно будет найти всего две точки.

Для примера построим график функции « y = −2x + 1 ».

Найдем значение функции « y » для двух произвольных значений « x ». Подставим, например, вместо « x » числа « 0 » и « 1 ».

Выбирая произвольные числовые значения вместо « x », лучше брать числа « 0 » и « 1 ». С этими числами легко выполнять расчеты.

x Расчет « y = −2x + 1 »

y(0) = −2 · 0 + 1 = 1

1 y(1) = −2 · 1 + 1 = −2 + 1 = −1

Полученные значения « x » и « y » — это координаты точек графика функции.

Запишем полученные координаты точек « y = −2x + 1 » в таблицу.

Точка Координата по оси « Оx » (абсцисса) Координата по оси « Оy » (ордината)

(·)A 1

(·)B 1 −1

Отметим полученные точки на системе координат.

Теперь проведем прямую через отмеченные точки. Эта прямая будет являться графиком функции « y = −2x + 1 ».

Как решать задачи на
линейную функцию « y = kx + b »

Построить график функции « y = 2x + 3 ». Найти по графику:

значение « y » соответствующее значению « x » равному −1; 2; 3; 5 ;

значение « x », если значение « y » равно 1; 4; 0; −1 .

Вначале построим график функции « y = 2x + 3 ».

Используем правила, по которым мы строили график функции выше. Для построения графика функции « y = 2x + 3 » достаточно найти всего две точки.

Выберем два произвольных числовых значения для « x ». Для удобства расчетов выберем числа « 0 » и « 1 ».

Выполним расчеты и запишем их результаты в таблицу.

Точка Координата
по оси « Оx » Координата
по оси « Оy »

(·)A y(0) = 2 · 0 + 3 = 3

(·)B 1 y(1) = 2 ·1 + 3 = 5

Отметим полученные точки на прямоугольной системе координат.

Соединим полученные точки прямой. Проведенная прямая будет являться графиком функции « y = 2x + 3 ».

Теперь работаем с построенным графиком функции « y = 2x + 3 ».

Требуется найти значение « y », соответствующее значению « x »,
которое равно −1; 2; 3; 5 .

Тему «Как получить координаты точки функции» с графика функции мы уже подробно рассматривали в уроке «Как решать задачи на функцию».

В этому уроке для решения задачи выше вспомним только основные моменты.

Чтобы найти значение « y » по известному значению « x » на графике функции необходимо:

провести перпендикуляр от оси « Ox » (ось абсцисс) из заданного числового значения « x » до пересечения с графиком функции;

из полученной точки пересечения перпендикуляра и графика функции провести еще один перпендикуляр к оси « Oy » (ось ординат);

полученное числовое значение на оси « Oy » и будет искомым значением.

По правилам выше найдем на построенном ранее графике функции « y = 2x + 3 » необходимые значения функции « y » для « x » равным −1; 2; 3; 5 .

Запишем полученные результаты в таблицу.

Заданное значение « x » Полученное с графика значение « y »

−1 1

2 7

3 9

5 13

Переходим ко второму заданию задачи. Требуется найти значение « x », если значение « y » равно 1; 4; 0; −1 .

Выполним те же действия, что и при решении предыдущего задания. Разница будет лишь в том, что изначально мы будем проводить перпендикуляры от оси « Oy » .

Запишем полученные результаты в таблицу.

Заданное значение « y » Полученное с графика значение « x »

−1 −2

−1,5

1 −1

4 0,5

Как проверить, проходит ли график через точку

Рассмотрим другое задание.

Не выполняя построения графика функции « y = 2x −

1

3

», выяснить, проходит ли график через точки с координатами (0; −

1

3

) и (1; −2) .

Чтобы проверить принадлежность точки графику функции нет необходимости строить график функции.

Достаточно подставить координаты точки в формулу функции (координату по оси « Ox » вместо « x », а координату по оси « Oy » вместо « y ») и выполнить арифметические расчеты.

Если получится верное равенство, значит, точка принадлежит графику функции.

Если получится неверное равенство, значит, точка не принадлежит графику функции.

Подставим в функцию « y = 2x −

1

3

» координаты точки (0; −

1

3

) .
−

1

3

= 2 · 0 −

1

3

−

1

3

= −

1

3

(верно)
Это означает, что график функции « y = 2x −

1

3

» проходит через точку с координатами (0; −

1

3

) .
Проверим точку с координатами (1; −2) . Также подставим координаты
в функцию « y = 2x −

1

3

».
−2 = 2 · 1 −

1

3

−2 = 2 −

1

3

−2 = 1

3

3

−

1

3

−2 = 1

2

3

(неверно)
Это означает, что график функции « y = 2x −

1

3

» не проходит через точку с координатами (1; −2) .

Как найти точки пересечения графика с осями

Найти координаты точек пересечения графика функции « y = −1,5x + 3 » с осями координат.

Для начала построим график функции « y = −1,5x + 3 » и на графике отметим точки пересечения с осями.

Для построения графика функции найдем координаты двух точек
функции « y = −1,5x + 3 ».

Выберем два произвольных числовых значения для « x » и рассчитаем значение « y » по формуле функции. Например, для x = 0 и x = 1 .

Точка Координата
по оси « Оx » Координата
по оси « Оy »

(·)A y(0) = −1,5 · 0 + 3 = 3

(·)B 1 y(1) = −1,5 · 1 + 3 = 1,5

Отметим полученные точки на системе координат и проведем через них прямую. Тем самым мы построим график функции « y = −1,5x + 3 ».

Теперь найдем координаты точек пересечения графика функции с осями по формуле функции.

Чтобы найти координаты точки пересечения графика функции
с осью « Oy » (осью ординат) нужно:

приравнять координату точки по оси « Ox » к нулю (x = 0) ;

подставить вместо « x » в формулу функции ноль и найти значение « y »;

записать полученные координаты точки пересечения с осью « Oy » .

Подставим вместо « x » в формулу функции « y = −1,5x + 3 » число ноль.

Чтобы найти координаты точки пересечения графика функции
с осью « Ox » (осью абсцисс) нужно:

приравнять координату точки по оси « Oy » к нулю (y = 0) ;

подставить вместо « y » в формулу функции ноль и найти значение « x »;

записать полученные координаты точки пересечения с осью « Oy » .

Подставим вместо « y » в формулу функции « y = −1,5x + 3 » число ноль.

Чтобы было проще запомнить, какую координату точки нужно приравнивать к нулю, запомните «правило противоположности».

Если нужно найти координаты точки пересечения графика с осью « Ox » , то приравниваем « y » к нулю.

И наооборот. Если нужно найти координаты точки пересечениа графика с осью « Oy » , то приравниваем « x » к нулю.

Алгебраические выражения

Содержание:

Алгебраические выражения. Основные понятия

Алгебраические выражения — это одна или несколько алгебраических величин (чисел и переменных), связанных между собой знаками арифметических операций: сложения, вычитания, умножения и деления, а также извлечения корня и возведения в степень (причём показатели корня и степени должны обязательно быть целыми числами) и знаками последовательности применения этих операций (обычно скобками различного вида). Количество величин, входящих в алгебраическое выражение, должно быть конечным.

Виды алгебраических выражений

Из чисел и переменных с помощью знаков сложения, вычитания, умножения, деления, возведения в рациональную степень и извлечения корня и с помощью скобок составляют алгебраические выражения.

Примеры алгебраических выражений:

Если алгебраическое выражение не содержит деления на переменные и извлечения корня из переменных (в частности, возведения в степень с дробным показателем), то его называют целым выражением. Из написанных выше целыми являются выражения 1), 2) и 6).

Если алгебраическое выражение составлено из чисел и переменных с помощью действий сложения, вычитания, умножения, возведения в степень с натуральным показателем и деления, причем используется деление на выражения с переменными, то его называют дробным выражением. Так, из написанных выше дробными являются выражения 3) и 4).

Целые и дробные выражения называют рациональными выражениями. Так, из написанных выше рациональными являются выражения 1), 2), 3), 4) и 6).

Если в алгебраическом выражении используется извлечение корня из переменных (или возведение переменных в дробную степень), то его называют иррациональным выражением. Так, из написанных выше иррациональными являются выражения 5) и 7).

Итак, алгебраические выражения могут быть рациональными и иррациональными. Рациональные выражения, в свою очередь, разделяются на целые и дробные.

Допустимые значения переменных. Область определения алгебраического выражения

Значения переменных, при которых алгебраическое выражение имеет смысл, называют допустимыми значениями переменных. Множество всех допустимых значений переменных называют областью определения алгебраического выражения (или областью допустимых значений переменных — ОДЗ).

Целое выражение имеет смысл при любых значениях входящих в него переменных. Так, при любых значениях переменных имеют смысл целые выражения 1), 2), 6) из п. 48.

Дробные выражения не имеют смысла при тех значениях переменных, которые обращают знаменатель в нуль. Так, дробное выражение 3) из п. 48 имеет смысл при всех , кроме = 1, а дробное выражение 4) имеет смысл при всех кроме значений

Иррациональное выражение не имеет смысла при тех значениях переменных, которые обращают в отрицательное число выражение, содержащееся под знаком корня четной степени или под знаком возведения в дробную степень. Так, иррациональное выражение 5) имеет смысл только при тех при которых а иррациональное выражение 7) имеет смысл только при (см. п. 48).

Если в алгебраическом выражении переменным придать допустимые значения, то получится числовое выражение; его значение называют значением алгебраического выражения при выбранных значениях переменных.

Пример:

Найти значение выражения

Решение:

Имеем

Понятие тождественного преобразования выражения. Тождество

Рассмотрим два выражения

При х = 2 имеем Числа 0 и 3 называют соответственными значениями выражений при х = 2. Найдем соответственные значения тех же выражений при х = 1:

Соответственные значения двух выражений могут быть равными друг другу (так, в рассмотренном примере выполняется равенство), а могут и отличаться друг от друга (так, в рассмотренном примере ).

Если соответственные значения двух выражений, содержащих одни и те же переменные, совпадают при всех допустимых значениях переменных, то выражения называют тождественно равными.

Тождеством называют равенство, верное при всех допустимых значениях входящих в него переменных.

Так, тождественно равны выражения

Пропорция (см. п. 30) есть тождество при всех значениях , кроме = 1, поскольку при = 1 знаменатели дробей обращаются в нуль, т. е. дроби не будут иметь смысла.

Замена выражения выражением (сократили на с) есть тождественное преобразование выражения при ограничениях Значит, = — тождество при всех значениях переменных, кроме Ь = 0, с = 0. Верные числовые равенства также называют тождествами.

Замену одного выражения другим, тождественно равным ему, называют тождественным преобразованием выражения.

Эта лекция взята со страницы полного курса лекций по изучению предмета “Математика”:

Смотрите также дополнительные лекции по предмету “Математика”:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Похожие записи:

Гипербола – определение, свойства и виды, уравнение

Число в нулевой степени – что это и как его вычислять

Степени чисел – возведение в степень в алгебре, таблица, правила

Теорема косинусов для треугольника – суть, как доказать