Онлайн урок: Координатная плоскость по предмету Математика 6 класс |

Урок 46 Бесплатно Координатная плоскость

До этого занятия мы обсуждали с вами только прямую и все, что с ней связано.

Сегодня урок посвятим изучению плоскости.

Узнаем, что называют координатной плоскостью и как получить её из обычной плоскости.

Познакомимся с прямоугольной системой координат на плоскости и разберем ее основные характеристики и особенности.

Выясним области применения и использования систем координат в практических целях и в жизни человека.

Научимся пользоваться прямоугольной системой координат на плоскости: определять координаты заданных точек и по заданным координатам точки находить ее положение на координатной плоскости.

Координатная плоскость и ее основные особенности

Представим движение автомобиля по прямолинейному участку дороги.

Любой прямолинейный участок дороги легко представить с помощью координатной прямой.

Координатная прямая позволяет нам связать точки на этой прямой с числом.

Вам уже известно, как из любой прямой получить координатную прямую.

Необходимо на прямой выбрать начало отсчета, задать направление и единичный отрезок (масштаб).

В результате с помощью координатной прямой вы однозначно определите, что конкретной точке на прямой соответствует ее единственное верное значение с соответствующим знаком.

И наоборот, если известна координата точки, то можно определить положение этой точки на координатной прямой.

Таким образом, для указания местоположения точки (в нашем случае автомобиля) на прямой нужна только одна координата на координатной оси.

В жизни часто приходится устанавливать положение точки по нескольким параметрам. В таком случае для однозначного определения положения точки требуется больше информации.

Предположим, купили мы билет на концерт.

Чтобы определить расположение конкретного кресла в зале, в билете указывают адрес места: номер ряда и номер кресла в ряду.

Так как каждому месту ставится в соответствие два числа, то для однозначного определения положения точки нам не будет хватать одной координатной прямой.

Для обозначения числами точного положения точки на плоскости используют математическую модель, которую называют координатной плоскостью.

Чтобы из обычной плоскости получить координатную, необходимо на этой плоскости задать определенную систему координат.

Существует различные системы координат.

Мы рассмотрим прямоугольную систему координат на плоскости.

Прямоугольной системой координат на плоскости называют систему из двух взаимно перпендикулярных прямых с общим началом отсчета и общей масштабной единицей.

Рассмотрим основные составляющие прямоугольной системы координат.

Две перпендикулярные прямые – это координатные оси:

Горизонтальная прямая – ось абсцисс (Ох).

Вертикальная прямая – ось ординат (Оу).

Точка пересечения координатных прямых – это начало координат (начало отсчета), её обозначают точкой О().

Единичный отрезок выбирается чаще всего одинаковый для каждой координатной оси.

Направление осей указывается стрелкой, каждая ось подписывается буквой.

Для координатных осей обычно выбирают положительное направление, т.е. «по умолчанию» принято использовать правостороннюю систему координат, в которой за положительное направление осей принимают ось ординат, направленную вверх, и ось абсцисс, направленную вправо.

Если приходится по каким-либо причинам использовать левостороннюю прямоугольную систему координат, то данный факт оговаривают в задаче.

Положение точки на плоскости определяется двумя упорядоченными числами: координатами х и y.

Координату точки по оси Ох называют абсцисса – х.

Координату точки по оси Оу называют ордината – y.

Координату точки на плоскости записывают так:

(х; y), причем обязательно на первом месте в скобках стоит абсцисса точки (х), а на втором – ордината этой точки (y)

Например, координата точки A:

A(2;-1), где

х = 2 (координата точки по оси Ох – абсцисса точки А)

y = –1 (координата точки по оси Оу – ордината точки А)

У меня есть дополнительная информация к этой части урока!

Чтобы запомнить порядок следования абсциссы и ординаты в записи координаты точки, часто используют такое сравнение:

Представьте, многоэтажный дом, а в нем вашу квартиру.

Чтобы попасть домой, первым делом вам необходимо зайти в нужный подъезд (координата по оси Ох), а затем подняться на нужный этаж (координата по оси Оу).

Координаты могут иметь различные числовые значения, в том числе быть равными нулю.

Если ордината точки равна нулю, то точка лежит на оси Ох.

Если абсцисса точки равна нулю, то точка лежит на оси Оу.

Оси координат разбивают плоскость на четыре части – координатные четверти (по-другому их называют координатные углы или квадранты).

Нумерация координатных плоскостей ведется против часовой стрелки римскими цифрами I, II, III, IV.

Если точка имеет положительную координату х (х > ) и положительную координату у (у > ), то она лежит в I координатной четверти.

Если точка имеет отрицательную координату х (х ), то она лежит во II координатной четверти.

История становления координатной системы уходит в глубину веков (IV век до н.э. – V век н.э.).

Античные ученые, мыслители (астрономы, философы, географы) на протяжении нескольких столетий пытались создать теорию о происхождении окружающего мира и всего мироздания в целом, изобразить известные им моря, океаны, страны в чертежах, а звездное небо на карте.

Благодаря великим умам появилось огромное множество фундаментальных знаний, понятий, представлений.

Появилось представление о Земле как о шаре, о ее расположение на звездном небе; создавались все более совершенные карты и планы, методы определения географических координат; на карту наносились линии широты и долготы, сетка параллелей и меридиан.

Долгое время лишь география и астрономия пользовались данными знаниями.

В XIV веке французский философ, астроном, математик Никола Орем пытался применить метод координат к геометрии.

Одной из самых важных математических работ Орема стал «Трактат о конфигурации качеств».

Именно в этой работе он ввел графическое изображение зависимости одной величины от другой с помощью прямоугольной системы координат, называя широтой и долготой то, что сейчас называют абсциссой и ординатой.

Это нововведение стало отправной точкой создания современного метода координат.

Научному обоснованию прямоугольной системы координат мы обязаны французскому ученому, философу Рене Декарту.

Он обобщил известные на то время знания по этой теме и дал научное истолкование прямоугольной системе координат.

Предложенная им прямоугольная система координат получила его имя, ее стали называть декартовой системой координат.

Координатный метод описания геометрических объектов положил начало аналитической геометрии.

Создание аналитической геометрии позволило переводить геометрические свойства тел и кривых на алгебраический язык, вместо геометрических построений использовать расчеты; кроме того, стало возможным анализировать геометрические объекты с помощью уравнений.

Развитием координатного метода и аналитической геометрии занимался также современник Рене Декарта, знаменитый французский ученый Пьер Ферма.

Однако все научные труды Ферма были опубликованы только после его смерти

Пройти тест и получить оценку можно после входа или регистрации

Прямоугольная система координат. Ось абсцисс и ординат

О чем эта статья:

Прямоугольная декартова система координат

Французский математик Рене Декарт преддложил вместо геометрических построений использовать математические расчеты. Так появился метод координат, о котором мы сейчас расскажем.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты школы тоже можно записать числами — они помогут понять, где именно находится наша школа. С точками на плоскости та же история.

Координатой можно назвать номер столика в кафе, широту и долготу на географической карте, положение точки на числовой оси и даже номер телефона друга. Проще говоря, когда мы обозначаем какой-то объект набором букв, чисел или других символов, тем самым мы задаем его координаты.

Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

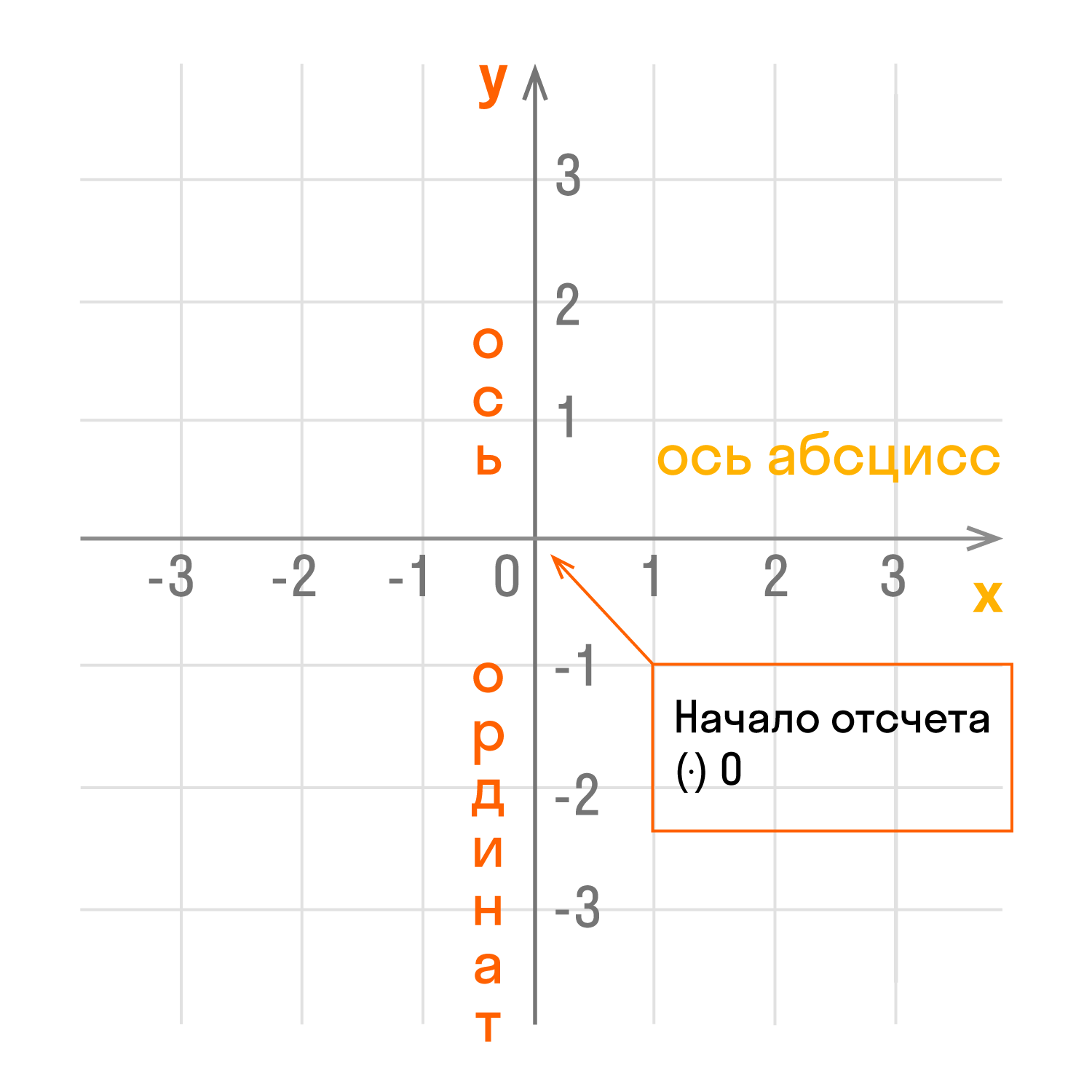
Координатные оси — это прямые, образующие систему координат.
Ось абсцисс Ox — горизонтальная ось.
Ось ординат Oy — вертикальная ось.
Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.

Единичные отрезки располагаются справа и слева от оси Oy, вверх и вниз от оси Oy. Числовые значения на оси Oy располагаются слева или справа, на оси Ox — внизу под ней. Чаще всего единичные отрезки двух осей соответствуют друг другу, но бывают задачи, где они не равны.

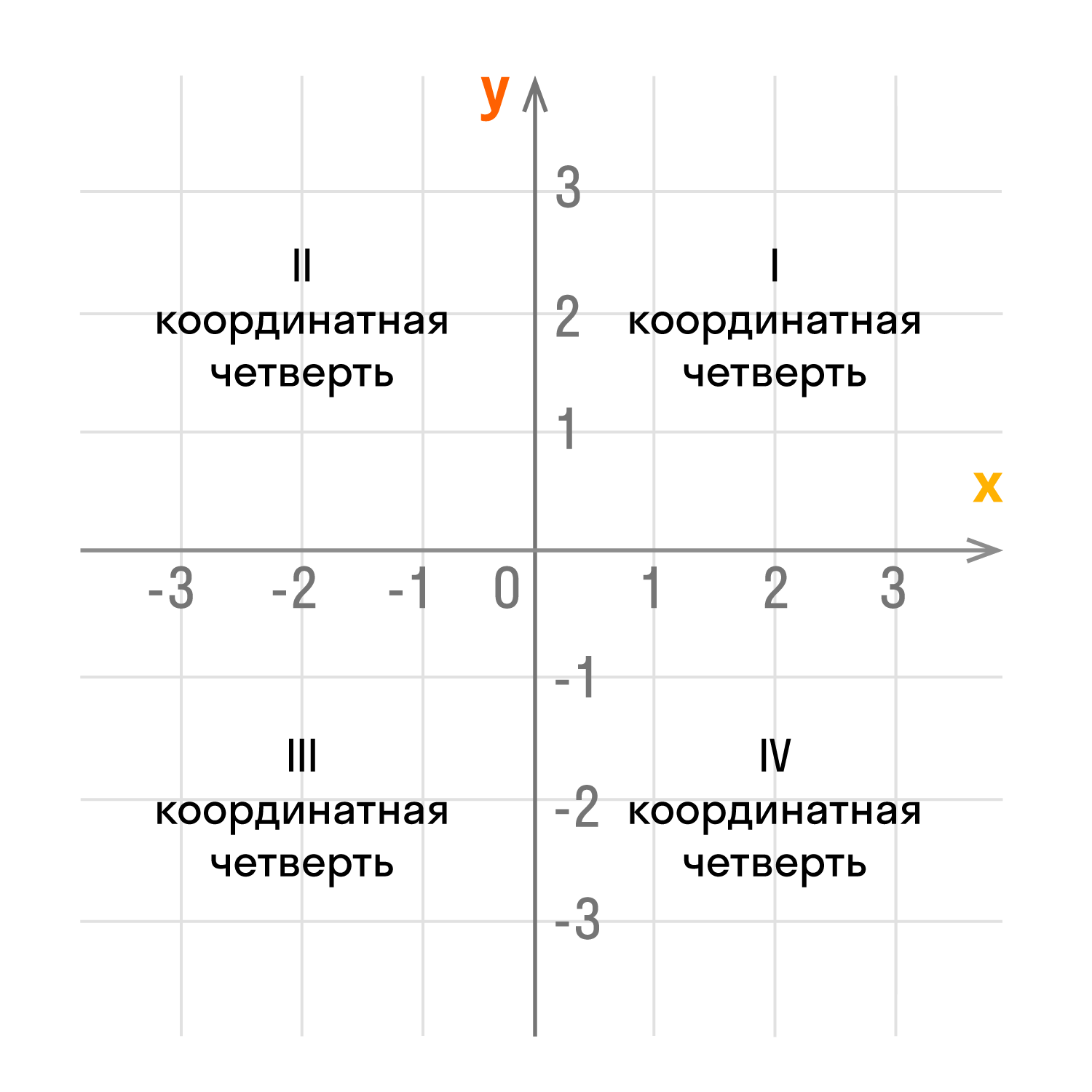
Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

верхний правый угол — первая четверть I;
верхний левый угол — вторая четверть II;
нижний левый угол — третья четверть III;
нижний правый угол — четвертая четверть IV;

Чтобы узнать координаты точки в прямоугольной системе координат, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра. Координаты записывают в скобках, первая по оси Ох, вторая по оси Оу.

Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
Если обе координаты отрицательны, то число находится в третьей четверти.
Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.

Прямоугольная система координат в трехмерном пространстве

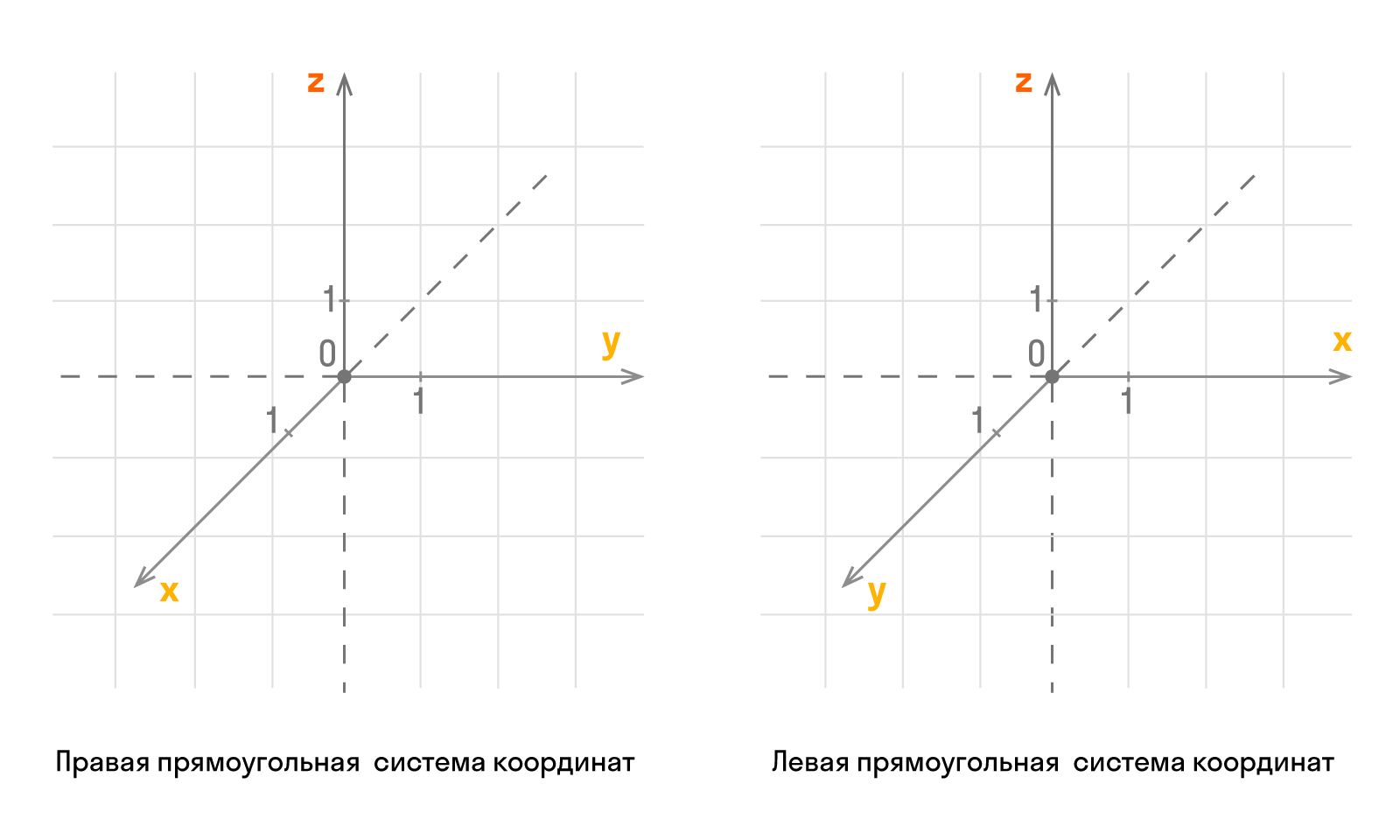
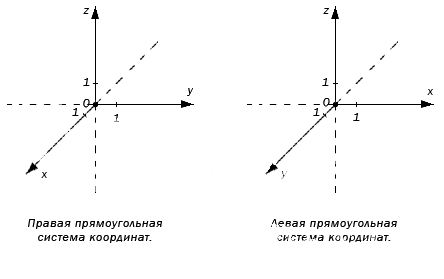
Трехмерное евклидово пространство состоит из трех взаимно перпендикулярных прямых: Ох, Оу, Оz, где Оz — ось аппликат. По направлению координатных осей есть разделение на правую и левую прямоугольные системы координат трехмерного пространства.

Оси координат пересекаются в точке О, которую называют началом. У каждой оси есть положительное направление, которое отмечается стрелкой. Если при повороте Ох против часовой стрелки на 90° ее положительное направление совпадает с положительным Оу, тогда это применимо для положительного направления Оz. Такую систему считают правой. Объясняем на пальцах! Если сравнить направление Х с большим пальцем руки, то указательный отвечает за Y, а средний за Z.

Также образуется левая система координат. Совмещать обе системы нет смысла, так как соответствующие оси не совпадут.

Координаты точки в декартовой системе координат

Для начала отложим точку М на координатной оси Ох. Любое действительное число x_M равно единственной точке М, которая располагается на данной прямой. При этом начало отсчета координатных прямых всегда ноль.

Каждая точка М, которая расположена на Ох, равна действительному числу x_M. Этим действительным числом и является ноль, если точка М расположена в начале координат, то есть на пересечении Оx и Оу. Если точка удалена в положительном направлении, то число длины отрезка положительно и наоборот.

Число x_M — это координата точки М на заданной координатной прямой.

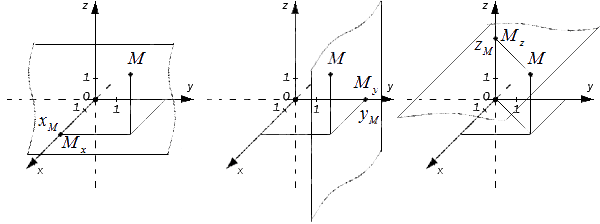
Пусть точка будет проекцией точки M_x на Ох, а M_y на Оу. Значит, через точку М можно провести перпендикулярные осям Оx и Оу прямые, после чего получим соответственные точки пересечения M_x и M_y.Тогда у точки M_x на оси Оx есть соответствующее число x_M, а M_y на Оу — y_M. Как это выглядит на координатных осях:

Каждой точке М на заданной плоскости в прямоугольной декартовой системе координат соответствует пара чисел (x_M, y_M), которые называются ее координатами. Абсцисса М — это x_M, ордината М — это y_M.

Обратное утверждение тоже верно: каждая пара (x_M, y_M) имеет соответствующую точку на плоскости.

Координаты точки в трехмерном пространстве

Сформулируем определение точки М в трехмерном пространстве.

Пусть M_x, M_y, M_z — это проекции точки М на соответствующие оси Оx, Оy, Оz. Тогда значения этих точек на осях примут значения x_M, y_M, z_M. Как это выглядит на координатных прямых:

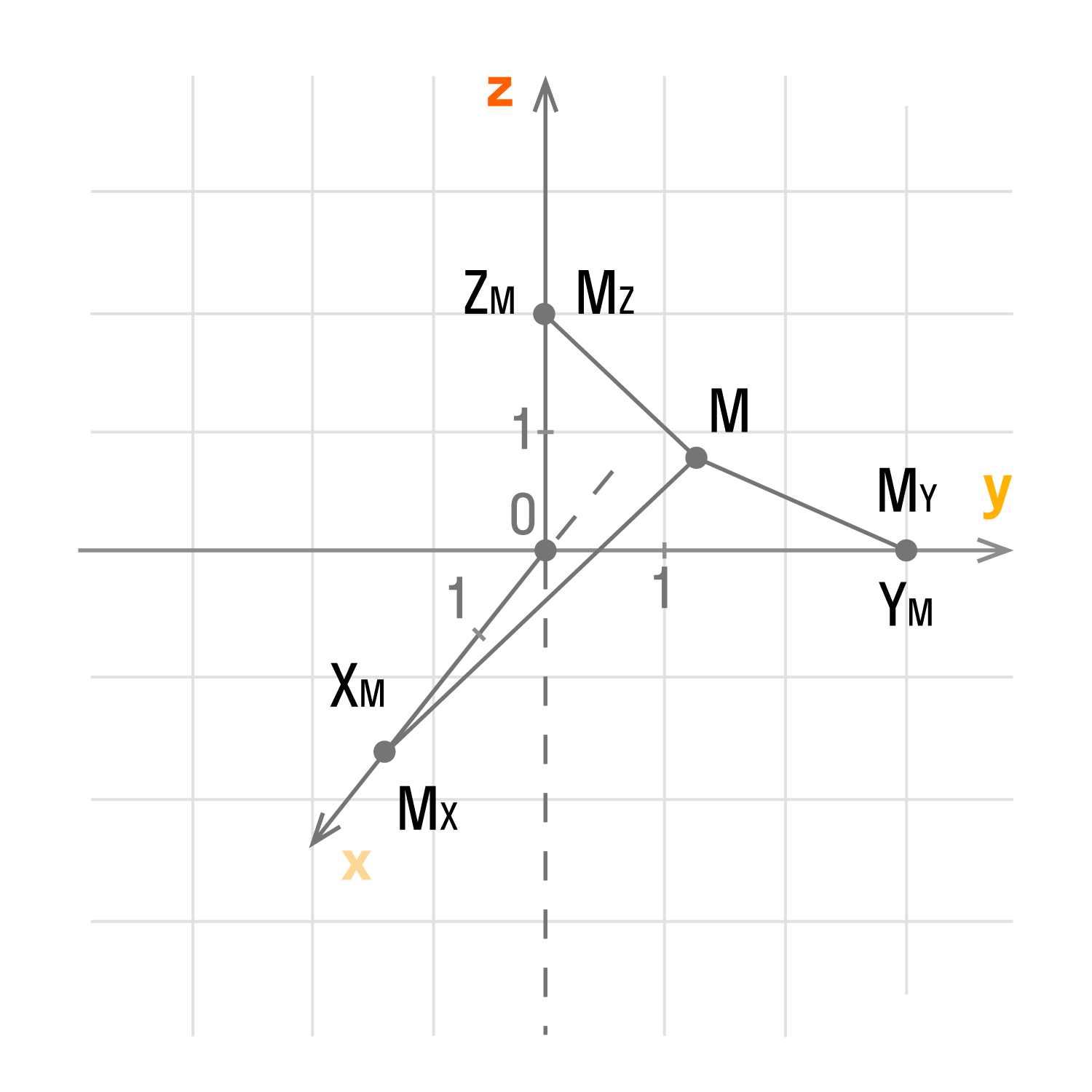
Чтобы получить проекции точки М, нужно добавить перпендикулярные прямые Оx, Оy, Оz, продолжить их и изобразить в виде плоскостей, которые проходят через М. Так плоскости пересекутся в M_x, M_y, M_z.

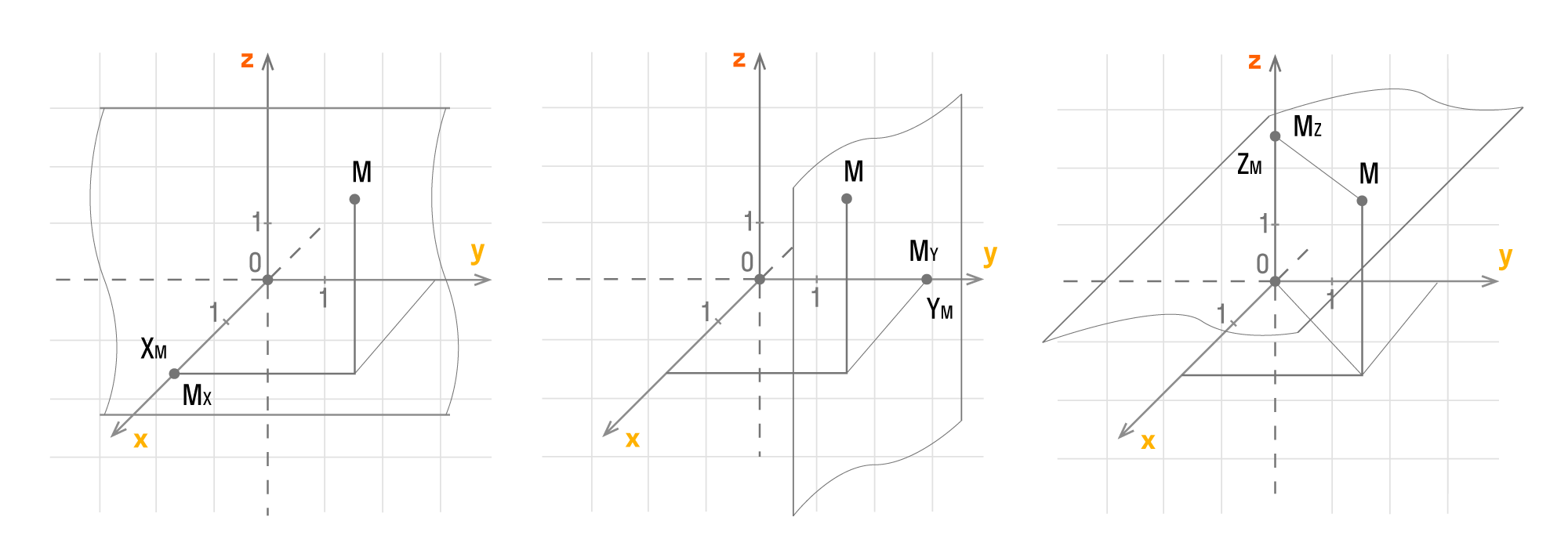
У каждой точки трехмерного пространства есть свои данные (x_M, y_M, z_M), которые являются координатами точки М.

x_M, y_M, z_M — это числа, которые являются абсциссой, ординатой и аппликатой данной точки М. Верно и обратное утверждение: каждая упорядоченная тройка действительных чисел (x_M, y_M, z_M) в заданной прямоугольной системе координат имеет одну соответствующую точку М трехмерного пространства.

Координатная плоскость

Урок 46. Математика 6 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока “Координатная плоскость”

В повседневной жизни вы могли слышать такую фразу: «Оставьте мне ваши координаты!».

Как вы понимаете эту фразу?

Это выражение означает, что собеседник должен оставить свой адрес или номер телефона, т.е. данные, по которым его можно найти.

Определение

Числа, с помощью которых указывают, где находится некоторый объект, называют его координатами.

С координатами вы уже не раз встречались и в математике. Вы умеете выполнять две операции: отмечать на координатной прямой точку с заданной координатой и, наоборот, определять координату заданной точки. Для этого на прямой выбирают начало отсчёта, положительное направление и единичный отрезок. После этого любая точка прямой получает свою собственную координату.

Координата точки указывает, таким образом, её место на координатной прямой.

Возникает вопрос: а можно ли определить местоположение точки на плоскости?

Наверняка, хоть раз в жизни вы играли в такую игру как «Морской бой».

Поле этой игры состоит из квадрата размерами 10 на 10 клеточек. В этом поле изображаются корабли: 1 четырёхклеточный, 2 трёхклеточных, 3 двухклеточных и 4 одноклеточных. При этом между любыми двумя соседними кораблями должен оставаться промежуток не меньше одной клетки.

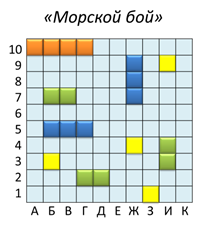
На экране изображён один из вариантов расположения кораблей. Каждая клеточка квадрата обозначается парой: (буква –число), указанных вдоль нижней и левой сторон квадрата. Например, корабль расположен в клетке (Ж; 4). Суть этой игры найти все корабли соперника первым. При обозначении положения клетки первой указывают её горизонтальную координату, а второй – вертикальную.

Именно в этом и состоит суть координат или, как обычно говорят, системы координат: это правило, по которому определяется положение того или иного объекта.

Системы координат встречаются в нашей жизни постоянно.

Вы знакомы с системой координат в зрительном зале кинотеатра (номер ряда и номер места), в поезде (номер вагона и номер места), с системой географических координат (долгота и широта).

Что нужно знать для того, чтобы найти своё место в кинотеатре? Места в зрительном зале кинотеатра задают двумя числами: первым числом обозначают номер ряда, а вторым – номер кресла в этом ряду. Значит, чтобы правильно занять своё место в зрительном зале необходимо знать две координаты: ряд и место.

Например, в билете указаны: 3 ряд 2 место. Посмотрите где это место расположено.

Обратите внимание, что при определении местоположения нам необходимо знать две характеристики или два значения.

Подобным образом можно обозначить и положение точки на плоскости.

Рене Декарт – французский математик ввёл в 1637 году систему координат, которая используется во всем мире и известна каждому школьнику. Её называют также «Декартова система координат».

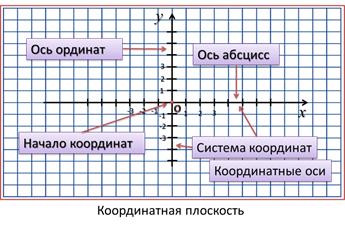
Чтобы задать декартову прямоугольную систему координат на плоскости проводят две взаимно перпендикулярные координатные прямые х и у, называемые координатными осями.

Точка пересечения осей – «O» называется началом координат.

На каждой оси ОX и ОY задаётся положительное направление и выбирается единичный отрезок.

Каждая из координатных осей имеет своё название: горизонтальную ось называют осью абсцисс (или осью х), вертикальную ось называют осью ординат (или осью у). Эти прямые составляют систему координат на плоскости.

Определение

Плоскость, на которой задана система координат, называется координатной плоскостью.

Оси разбивают координатную плоскость на четыре части, которые называют координатными четвертями. Их нумеруют римскими цифрами и против часовой стрелки.

Говорят: первая четверть, вторая четверть, третья четверть и четвертая четверть.

Каждая точка такой плоскости имеет две координаты.

Рассмотрим, как определяется положение точки на координатной плоскости.

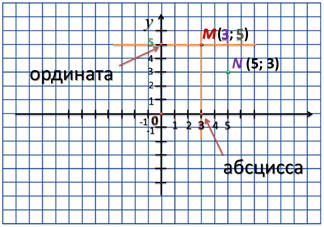
Например, у нас есть точка М. И нужно определить её координаты. Для этого проведём перпендикуляр из этой точки на горизонтальную ось или ось абсцисс.

Точка пересечения с осью х называется абсциссой точки М.

В нашем случае, абсцисса точки М 3.

Далее, из этой же точки проведём перпендикуляр до пересечения с вертикальной осью, или осью ординат.

Точка пересечения с осью у называется ординатой точки М.

В нашем случае, ордината точки М 5.

Абсцисса и ордината точки М называются координатами этой точки. Их принято записывать рядом с буквой, обозначающей точку, в круглых скобках. Причем, на первом месте всегда пишется абсцисса, а на втором – ордината.

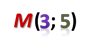
Читают эту запись так: «точка М с абсциссой 3 и ординатой 5», или «точка М с координатами 3 и 5». Обратите внимание, если переставить координаты местами, то получится совсем другая точка. Например, точка N (5; 3).

Определение

Координаты точки (х;у) на плоскости – это пара чисел, в которой на первом месте стоит абсцисса (х), а на втором – ордината (у) этой точки.

Сделаем вывод: координаты можно указать для любой точки координатной плоскости: для этого надо из точки провести перпендикуляры на координатные оси и определить, какому числу координатной оси соответствует основание перпендикуляра.

Точки любой прямой, перпендикулярной оси абсцисс, имеют одну и ту же абсциссу.

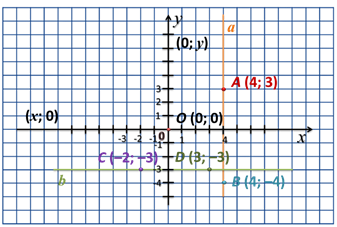
Например, все точки прямой а имеют абсциссу 4. Все точки оси ординат имеют абсциссу 0, т.е. координаты любой точки оси ординат имеют вид (0; у).

Точки любой прямой, перпендикулярной оси ординат, имеют одну и ту же ординату.

Например, все точки прямой b имеют ординату -3. Все точки оси абсцисс имеют ординату 0, т.е. координаты любой точки оси абсцисс имеют вид (х; 0).

Начало координат – точка О – лежит и на оси абсцисс, и на оси ординат. Значит, её координаты (0; 0).

Построить точку по её координатам можно несколькими способами.

Например, построим точку А (-5; 7).

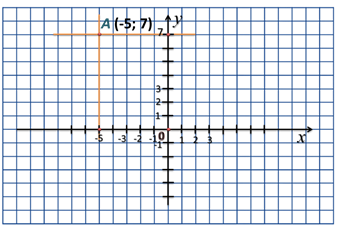
Первый способ: на оси х находим абсциссу точки А. Она у нас равна -5. Проводим перпендикуляр из этой точки относительно оси ОХ. Далее, на оси у, найдём ординату точки. Она равна 7. Проводим перпендикуляр из этой точки относительно оси ОУ. Точка, где пересеклись оба перпендикуляра, и есть искомая точка А.

Второй способ построения точки по заданным координатам. Можно сместиться по оси ОХ влево на 5 единиц, т.к. абсцисса точки – отрицательное число. А затем, параллельно оси ОX вверх на 7 единиц, т.к. ордината точки положительное число. Точка, где пересеклись оба перпендикуляра, и есть искомая точка А.

Сделаем ещё один очень важный вывод:

Каждой точке на координатной плоскости соответствует пара чисел: её абсцисса и ордината. Наоборот, каждой паре чисел соответствует одна точка плоскости, для которой эти числа являются координатами.

Задание

Построите на координатной плоскости точки, а затем последовательно соедините их отрезками.

Какая фигура у нас получилась в итоге? Правильно! Это котик.

Прямоугольная система координат

Содержание

Иногда в жизни, чтобы найти на плоскости какой-то объект, его описывают двумя значениями. Так каждое место в зале кинотеатра имеет два параметра: ряд и место. Каждая клетка на шахматной доске или при игре в «морской бой» описывается номером строки и буквой, обозначающей столбец.

В математике определение местоположения объекта на плоскости придумали быстро находить с помощью системы координат, образованной двумя прямыми, называемых координатными осями (или осями координат).

Ось координат

Абсцисса, ордината, начало координат и единичный отрезок

Эти оси имеют общепринятые наименования. А именно, горизонтальную ось именуют осью абсцисс и на письме обозначают $Ох$

Вертикальную ось называют осью ординат и на письме обозначают $Оу$

Оси пересекаются под прямым углом перпендикулярно друг к другу, поэтому такая система координат и называется прямоугольной.

Место пересечения осей координат является началом отсчета. Обычно эту точку обозначают буквой $О$ и называют началом координат. Ее называют еще иногда нулевой точкой.

На каждой оси выбирается единичный отрезок, с помощью которого вычисляются координаты объекта. Длиной единичного отрезка может выступать любая единица измерения, но она должна быть одинаковой на каждой из осей. То есть, если единичный отрезок на оси абсцисс задан, например, равным 1 см, то и на оси ординат единичный отрезок тоже должен быть равен одному сантиметру.

Абсцисса, ордината, начало координат и единичный отрезок

Положительное и отрицательное направление

У осей стрелкой задается положительное направление:

так обычно у оси $Ох$ положительным считается направление вправо;
у оси $Оу$ положительным считается направление снизу вверх.

В таком случае часть прямой $Ох$ левее точки $О$ будет принимать отрицательные значения. Аналогично часть прямой $Оу$ ниже точки отсчета $О$ будет также принимать отрицательные значения.

Таким образом, все вместе:

начало координат $О$
пересекающиеся под прямым углом оси $Ох$ и $Оу$ с заданными направлениями
заданный единичный отрезок

образуют в математике прямоугольную систему координат, плоскость называют координатной.

Или другими словами:

На письме система координат обозначается $Оху$

Четверти

Осями координат плоскость делится на 4 части, их обозначают римскими цифрами. Каждая часть называется «квадрант». Другие названия: «координатный угол» или «четверть». Нумерация четвертей принята против часовой стрелки в том порядке, в котором указано на рисунке ниже.

Четверти координатной плоскости

В квадранте I значения $х$ и $у$ будут больше 0 (или положительными). Отсюда следует, что если координаты объекта $х$ и $у$ – числа положительные, то он находится в I квадранте.

В квадранте II значения $у$ будут также положительными, а координаты $х$ будут иметь знак минус.

В квадранте III обе координаты $х$ и $у$ будут иметь отрицательные значения.

В последнем IV квадранте значение $х$ будет положительным, а $у$ отрицательным.

Немного из истории

В латинском языке слово «координаты» получилось из двух других: co – «совместно» и ordinatus – «определенный», «упорядоченный».

Впервые необходимость нахождения координат объектов возникла в географии и астрономии. Для этого использовали широту и долготу, определяющие расположение точки на небесной сфере или на поверхности земного шара. Таким образом начали вычислять координаты точек еще в 14 веке. Но упорядочил и систематизировал все знания в 17 веке французский математик по имени Рене Декарт. Поэтому прямоугольную систему координат также называют еще и «декартовой».

Прямоугольная система координат на плоскости и в пространстве

При введении системы координат на плоскости или в трехмерном пространстве появляется уникальная возможность описания геометрических фигур и их свойств при помощи уравнений и неравенств. Это имеет иное название – методы алгебры.

Данная статья поможет разобраться с заданием прямоугольной декартовой системой координат и с определением координат точек. Более наглядное и подробное изображение имеется на графических иллюстрациях.

Прямоугольная декартова система координат на плоскости

Чтобы ввести систему координат на плоскости, необходимо провести на плоскости две перпендикулярные прямые. Выбираем положительное направление, обозначая стрелочкой. Необходимо выбрать масштаб. Точку пересечения прямых назовем буквой O . Она считается началом отсчета. Это и называется прямоугольной системой координат на плоскости.

Прямые с началом O , имеющие направление и масштаб, называют координатной прямой или координатной осью.

Прямоугольная система координат обозначается O x y . Координатными осями называют О х и О у , называемые соответственно ось абсцисс и ось ординат.

Изображение прямоугольной системы координат на плоскости.

Оси абсцисс и ординат имеют одинаковую единицу изменения и масштаб, что показано в виде штрихе в начале координатных осей. Стандартное направление О х слева направо, а O y – снизу вверх. Иногда используется альтернативный поворот под необходимым углом.

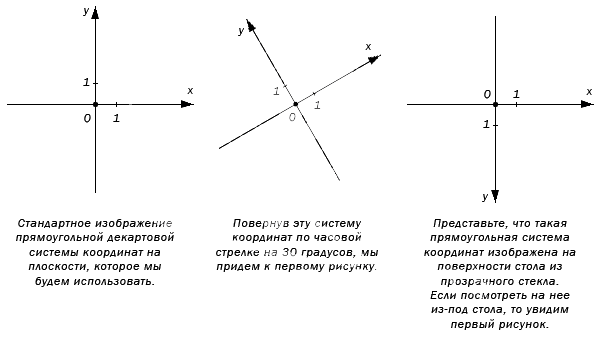
Прямоугольная система координат получила название декартовой в честь ее первооткрывателя Рене Декарта. Часто можно встретить название как прямоугольная декартовая система координат.

Прямоугольная система координат в трехмерном пространстве

Трехмерное евклидовое пространство имеет аналогичную систему, только оно состоит не из двух, а из трех О х , О у , О z осей. Это три взаимно перпендикулярные прямые, где О z имеет название ось аппликат.

По направлению координатных осей делят на правую и левую прямоугольные системы координат трехмерного пространства.

Оси координат пересекаются в точке O , называемой началом. Каждая ось имеет положительное направление, которое указывается при помощи стрелок на осях. Если при повороте О х против часовой стрелки на 90 ° ее положительное направление совпадает с положительным О у , тогда это применимо для положительного направления О z . Такую систему считают правой. Иначе говоря, если сравнить направление Х с большим пальцем руки, то указательный отвечает за Y , а средний за Z .

Аналогично образуется левая система координат. Обе системы совместить невозможно, так как соответствующие оси не совпадут.

Координаты точки в декартовой системе координат на плоскости

Для начала отложим точку М на координатной оси О х . Любое действительное число x M равняется единственной точке М , расположенной на данной прямой. Если точка расположена на координатной прямой на расстоянии 2 от начала отсчета по положительному направлению, то она равна 2 , если – 3 , то соответственное расстояние 3 . Ноль – это начало отсчета координатных прямых.

Иначе говоря, каждая точка М , расположенная на O x , равна действительному числу x M . Этим действительным числом и является ноль, если точка M расположена в начале координат, то есть на пересечении O x и О у . Число длины отрезка всегда положительно, если точка удалена в положительном направлении и наоборот.

Имеющееся число x M называют координатой точки М на заданной координатной прямой.

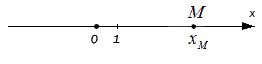
Возьмем точку как проекцию точки M x на О х , а как проекцию точки M y на О у . Значит, через точку М можно провести перпендикулярные осям О x и О у прямые, где послучим соответственные точки пересечения M x и M y .

Тогда точка M x на оси О х имеет соответствующее число x M , а M y на О у – y M . На координатных осях это выглядит так:

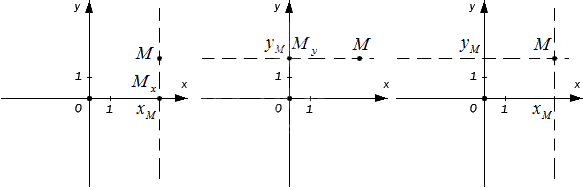
Каждая точка M на заданной плоскости в прямоугольной декартовой системе координат имеет одну соответствующую пару чисел ( x M , y M ) , называемую ее координатами. Абсцисса M – это x M , ордината M – это y M .

Обратное утверждение также считается верным: каждая упорядоченная пара ( x M , y M ) имеет соответствующую заданную в плоскости точку.

Координаты точки в прямоугольной системе координат в трехмерном пространстве

Определение точки М в трехмерном пространстве. Пусть имеются M x , M y , M z , являющиеся проекциями точки М на соответствующие оси О х , О у , О z . Тогда значения этих точек на осях О х , О у , О z примут значения x M , y M , z M . Изобразим это на координатных прямых.

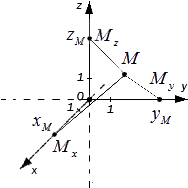
Чтобы получить проекции точки M , необходимо добавить перпендикулярные прямые О х , О у , О z продолжить и изобразит в виде плоскостей, которые проходят через M . Таким образом, плоскости пересекутся в M x , M y , M z

Каждая точка трехмерного пространства имеет свои данные ( x M , y M , z M ) , которые имеют название координаты точки M , , x M , y M , z M – это числа, называемые абсциссой, ординатой и аппликатой заданной точки M . Для данного суждения верно и обратное утверждение: каждая упорядоченная тройка действительных чисел ( x M , y M , z M ) в заданной прямоугольной системе координат имеет одну соответствующую точку M трехмерного пространства.

Координатная плоскость — определение расположения точек и фигур

Чтобы указать расположение точки или фигуры в двумерном пространстве, используется координатная плоскость.

С помощью этой системы осуществляется решение задач в геометрии, а также в других научных дисциплинах.

Кроме того, принцип указания точного адреса объекта с помощью двух величин получил широкое распространение во многих отраслях человеческой деятельности.

Системы координат

Под понятием координат в повседневной жизни понимается упорядоченный набор слов, цифр и прочих знаков, позволяющий определить местоположение человека, здания или другого объекта. Эти знания необходимы для ориентирования в современном обществе и организации любой человеческой деятельности.

Трудно даже представить себе мир без системы адресов и нумерации.

Примеры использования:

почтовый адрес;
номер места в театре, автобусе или самолёте;
обозначение положения фигур на шахматной доске;
географическая широта и долгота.

Таким образом, система координат необходима не только в математике.

Она буквально пронзает всю человеческую жизнь.

Без применения этих научных знаний люди не смогли бы значительно отдалиться от животных и первобытных предков.

Некоторые области применения:

Геометрия довольно часто пользуется методикой нахождения точки на координатной плоскости или в пространстве.

Математика — построение графиков функций.

География использует собственные координаты (широта и долгота).

Астрономия определяет положение небесных объектов во вселенной.

По определению любая координатная система представляет собой ряд идентификационных данных, которые позволяют узнать положение точки или фигуры в пространстве, а также дают возможность проследить её перемещение.

Наибольшее распространение получила прямоугольная система координат, которую ещё называют декартовой, по имени создателя Рене Декарта. Её популярность основана на простоте и универсальности.

Другие виды координат:

полярные;
цилиндрические;
сферические;
косоугольные;
биангулярные;
биполярные;
конические;
бицентрические;
координаты Риндлера;
бицилиндрические;
параболические;
тороидальные;
проективные;
трилинейные;
эллипсоидальные.

Видя такое множество, можно смело сказать, что задать координаты на плоскости, в двумерном или трёхмерном пространстве можно бесчисленным количеством способов. Для решения определённой задачи стоит выбирать наиболее подходящий метод из всех имеющихся.

Координатная плоскость

Прямоугольная или квадратная система координат была изобретена ещё в XVII веке. Благодаря своей невероятной гениальности, простоте и понятности для большинства людей, она получила широчайшее распространение и с успехом применяется до сих пор.

Чтобы построить фигуру на координатной плоскости, нужно изобразить две линии пересекающиеся под прямым углом:

Ось X’X.

Ось Y’Y.

Точка пересечения O является началом отсчёта, из неё откладываются все значения в координатной системе. Стоит помнить, что вправо и вверх идут положительные величины, а влево и вниз — отрицательные. Таким образом, две оси образуют квадранты координатной плоскости (четверти). В зависимости от того, в каком из четырёх образовавшихся сегментов находится точка или фигура, будет изменяться её значение.

Местоположение любой точки на координатной плоскости определяется при помощи двух числовых показателей. Первый — это абсцисса x, он откладывается по горизонтали и равен отрезку ОВ. Второй — ордината y, откладывающаяся по вертикали и совпадающая с отрезком ОС.

Выходит, что для задания и записи точного местоположения любой точки А необходимо измерить её расстояние до оси абсцисс и ординат. Схематическая запись координат будет выглядеть как А (x, y) или xА, xB, возможны и другие варианты.

Обычно на практике применяют правостороннюю координатную систему. В этом случае адрес точки принимает положительное значение лишь в правом верхнем квадранте I, образованном правой частью оси ординат (X) и верхней частью оси абсцисс (Y). Иногда бывают ситуации, в которых использование другой ориентации является более целесообразным.

Не стоит считать, что декартовая координатная система может применяться только на плоскости. Она вполне подходит для любого пространства, имеющего конечную размеренность. Всё становиться более сложным — для каждого дополнительного измерения создаётся новая ось.

Для нахождения местоположения точек в привычном трёхмерном пространстве, помимо абсциссы и ординаты, вводится третья координата, именуемая аппликатором (z). Для этого через точку O проводится дополнительная ось, изображающая третье измерение и являющаяся перпендикулярной к двум остальным. В этом случае создаётся своеобразная объёмная решётка, а пространство разделяется линиями на 8 частей — октантов.

При рисовании такой системы на листе применяется проекция на плоскость. Третья ось проводится под углом в 45 градусов к остальным, создавая иллюзию трёхмерного пространства.

Историческая справка

Сегодня каждый школьник, учащийся в шестом классе, не только слышал про координатную плоскость, но и знает правило построения простейших фигур в двумерном пространстве. Но так было не всегда.

Необходимость в определении точного местоположения объектов возникла очень давно. Скорее всего, ещё в древнейшие времена существовали примитивные методы записи координат. Более точные системы возникли в Древней Греции. Их появление было связано с потребностью в картографии.

Достоверно известно, что составитель первой карты Анаксимандр Милетский пользовался географической долготой и широтой, запись которых была основана на прямоугольной проекции. Незадолго до начала нашей эры древнегреческий учёный по имени Гиппарх выдвинул замечательную идею, заключающуюся в опоясывании земного шара параллелями и меридианами и записи информации о положении объектов в виде двух чисел. В Египте на стене одной из усыпальниц археологами был обнаружен рисунок, состоящий из клеточек и представляющий собой координатную сетку.

Автором прямоугольной системы координат на плоскости является математик Рене Декарт, живший во Франции XVII века. История этого гениального открытия весьма забавна. Дело в том, что в театре тех лет ещё не существовало привычной для современной публики нумерации мест. Из-за этого нередко возникала страшная путаница, ссоры, драки и даже дуэли. Будучи талантливым математиком, Декарт предложил новый способ обозначения, базирующийся на двух номерах — ряда и кресла. Это изобретение избавило зрителей от ненужных проблем и произвело настоящий фурор в обществе.

Позже учёный изложил принципы плоскости координат, а также прочие открытия в своём фундаментальном труде «Геометрия». Первые попытки применить метод Декарта к трёхмерному пространству были предприняты в XVIII веке Леонардом Эйлером.

Сегодня при помощи декартовой системы координат можно задать не только расположение простой фигуры, например, треугольника, на плоскости, но и описать любой сложный предмет и его перемещение в пространстве. Метод нашёл широкое применение во многих электронных устройствах и графических программах.

Особенности использования в географии

С развитием современных технологий определение географических координат очень упростилось.

Достаточно запустить одно из навигационных приложений или войти в специальный онлайн-сервис, и местоположение будет указано с максимальной точностью.

Поверхность земли имеет сферическую форму, из-за этого географическая система координат имеет свои особенности.

Обозначение любой точки на планете осуществляется при помощи набора цифробуквенных обозначений:

широта бывает северная и южная;
долгота — восточная и западная;
высота над уровнем моря.

Все точки одной широты соединяются параллелями. На экваторе широта составляет 0 градусов, а на полюсе 90. Меридианы соединяют точки с одним и тем же показателем долготы и сходятся на полюсах.

Обыкновенные дроби

теория по математике 📈 числа и вычисления

Обыкновенная дробь – это запись числа в виде:

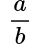
где число a называют числителем, а число b – знаменателем дроби.

Основное свойство дроби

Если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь.

Пример №1. У первой дроби можно разделить числитель и знаменатель на одно и то же число 14, и получится равная ей дробь. Или как у второй дроби можно умножить числитель и знаменатель на одно и то же число, допустим, на 5.

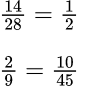Основное свойство дроби в основном применяют при сокращении обыкновенных дробей. Обыкновенные дроби бывают сократимые и несократимые.

Сократимые – это дроби, у которых числитель и знаменатель делятся на одно и то же число.
Несократимые – это дроби, у которых числитель и знаменатель не имеют общих делителей.

Сокращение дробей

Сократить дробь – значит разделить числитель и знаменатель на одно и то же число.

Пример №2. Чтобы сократить данную дробь надо вспомнить признаки делимости и увидеть, что числитель и знаменатель дроби — четные числа, значит, их можно разделить на 2, то есть дробь сокращается на 2:

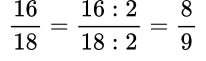
Пример №3. По признаку делимости числитель и знаменатель делятся на 5, значит, сокращается данная дробь на 5.

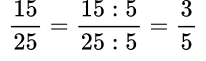Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями

При сложении (вычитании) обыкновенных дробей с одинаковыми знаменателями нужно знаменатель оставить тем же, а числители сложить (вычесть). Если дроби смешанные, то отдельно складывают (вычитают) целые части.

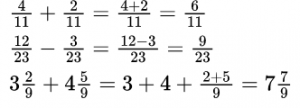
Решения можно записывать короче, выполняя устно сложение или вычитание целых частей, а также – числителей.

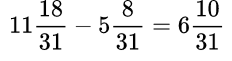
Вычитание обыкновенной дроби из целого числа

Чтобы вычесть дробь из единицы, нужно единицу представить в виде неправильной дроби, числитель и знаменатель которой равны знаменателю вычитаемой дроби.

Пример №5. Представляем единицу в виде дроби и получаем вычитание дробей с одинаковыми знаменателями (числители можно вычесть устно).

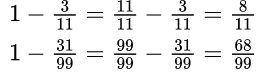Вычитание обыкновенной дроби из бóльшего числа

Чтобы вычесть обыкновенную дробь из числа, большего 1, необходимо представить эту дробь в виде смешанного числа, числитель и знаменатель которой равны также знаменателю вычитаемой дроби.

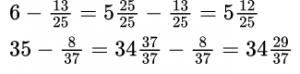
Сложение и вычитание дробей с разными знаменателями

Сложение и вычитание дробей с разными знаменателями требует предварительного приведения дробей к общему знаменателю. Существуют несколько приемов, которыми можно воспользоваться для нахождения общего знаменателя.

Нахождение общего знаменателя

Наименьшее общее кратное (НОК) – это наименьшее число, которое делится без остатка на данные знаменатели одновременно. Обычно его находят устно при выполнении действий с дробями.

Правило нахождения НОК рассмотрим на примере чисел 12 и 15. Пример №7. 1. Нужно разложить на простые множители каждое число:

2. Затем найти одинаковые множители (подчеркиваем):

В данном случае это только множитель 3.

3. Взять одно из данных чисел и домножить на оставшиеся (не подчеркнутые) множители другого числа:

12 домножаем на 5: 12×5=60, или

15 домножаем на 2 и 2: 15×2×2=60

Таким образом, НОК =60. Обычно достаточно просто внимательно посмотреть на числа и в уме подобрать для них НОК.

Перемножение знаменателей. Приём №2.

Нам необходимо просто перемножить знаменатели. Обычно этот прием используется тогда, когда даны простые числа (которые делятся на 1 и на само себя) и на множители их не разложить.

Пример №8.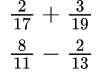

Для нахождения общего знаменателя в первом случае: 17×19=323, во втором: перемножаем 11 и 13, получаем 143.

Последовательный подбор. Приём №3.

Данный способ можно применить для небольших чисел устно: возьмем больший из знаменателей, умножим его на 2 и проверим, делится ли это число на второй знаменатель. Если нет, то умножим последовательно на 3, 4 и проверим аналогично.

Пример №9. Возьмем число 51, умножим на 2, получим 102 — видим, что 102 делится на 34, поэтому 102 и будет общий знаменатель.

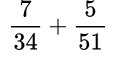
После того, как мы научились находить общий знаменатель, приступаем непосредственно к алгоритму сложения (или вычитания) обыкновенных дробей с разными знаменателями.

Алгоритм сложения (вычитания)

Находим общий знаменатель данных дробей.
Находим дополнительный множитель к числителю каждой дроби, разделив общий знаменатель на числитель каждой дроби.
Умножаем каждый числитель на дополнительный множитель.
Выполняем сложение (вычитание) дробей с одинаковыми знаменателями.

Пример №10.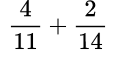

Находим общий знаменатель. Можно использовать прием, когда умножаем 11 и 14, так как 11 — простое число. Следовательно, общий знаменатель равен 154. Находим дополнительный множитель к каждому числителю:

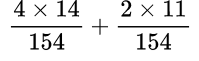Выполняем умножение в числителе: 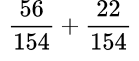Выполняем сложение дробей с одинаковыми знаменателями: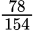

Умножение обыкновенных дробей

При умножении обыкновенных дробей получают дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.

При умножении обыкновенной дроби и целого числа необходимо целое число представить в виде дроби, числитель которой равен этому числу, а знаменатель равен 1 (что по сути означает перемножение числителя единственной первой дроби и целого числа, знаменатель же остается от первой дроби, так не меняется при умножении на единицу).

Если даны смешанные дроби, то необходимо сначала смешанную дробь перевести в неправильную, а затем выполнить умножение.

Пример №11. Здесь числитель 3 умножили на числитель 7, знаменатель 5 на знаменатель 10.

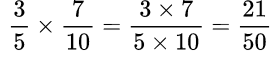
Пример №12. Случай, когда мы находим произведение дроби и целого числа. Целое число представили в виде дроби со знаменателем 1.

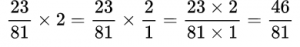
Пример №13. Нам даны смешанные дроби, переводим их в неправильные для выполнения умножения.

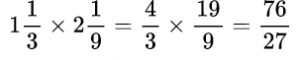
Деление обыкновенных дробей

При делении обыкновенных дробей необходимо делимое (то есть первую дробь) умножить на перевернутую вторую дробь, то есть дробь, обратную второй.

Если даны смешанные числа, то перед выполнением деления их необходимо перевести в обыкновенные неправильные дроби.

Если дробь нужно разделить на целое число, то его сначала нужно представить в виде дроби, а затем выполнить деление по правилу.

Пример №14. Делимое умножаем на число, обратное делителю. 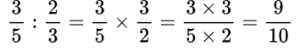Пример №15. Смешанные дроби сначала переводим в неправильные, а затем выполняем деление.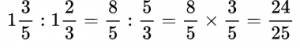

Пример №16. Деление дроби на целое число, где целое число 7 представлено в виде обыкновенной дроби.

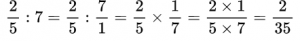
Найдите значение выражения:

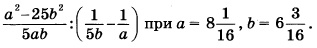
Упрощение заданного выражения нужно начать с преобразований в скобках. Здесь следует привести дроби к общему знаменателю:

теперь переходим от деления дробей к их умножению:

затем 1) сокращаем дроби на 5ab; 2) в числителе первой дроби раскладываем выражение, используя формулу сокращенного умножения для разности квадратов:

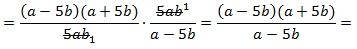сокращаем выражение на (a–5b): Представим числовые значения для a и b в виде неправильных дробей (для удобства вычислений): Подставим полученные значения в выражение и найдем конечный результат: 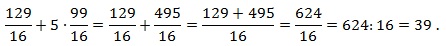Ответ: 39

pазбирался: Даниил Романович | обсудить разбор | оценить

Найдите значение выражения при x = 12:

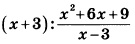
Выполним тождественные преобразования выражения, чтобы упростить его. 1-й шаг – переход от деления дробей к их умножению:

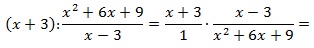
далее в знаменателе второй дроби сворачиваем выражение по формуле сокращенного умножения (используем ф-лу для квадрата суммы):

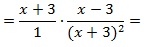
теперь сокращаем выражение (в числителе первой дроби и в знаменателе второй) и приходим к окончательно упрощенному виду:

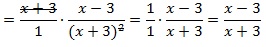
Подставляем числовое значение для х в полученное выражение и находим результат:

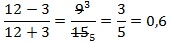Ответ: 0,6

pазбирался: Даниил Романович | обсудить разбор | оценить

Найдите значение выражения

В первую очередь в заданиях такого типа необходимо упростить выражение, а затем подставить числа. Приведем выражение к общему знаменателю — это b, для этого умножим первое слагаемое на b, после этого получим в числителе:

Приведем подобные слагаемые — это 9b² и — 9b², в числителе остается 5a. Запишем конечную дробь:

Вычислим её значение, подставив числа из условия:

pазбирался: Даниил Романович | обсудить разбор | оценить

Найдите значение выражения:

при x = √45 , y = 0,5

Итак, в данном задании при вычитании дробей нам необходимо привести их к общему знаменателю. Общий знаменатель — это 15 x y, для этого необходимо первую дробь домножить на 5 y — и числитель и знаменатель, естественно:

Далее, после того как дроби приведены к общему знаменателю, можно производить вычисления. Вычислим числитель:

5 y — (3 x + 5 y) = 5 y — 3 x — 5 y = — 3 x

Тогда дробь примет вид:

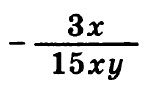
Выполнив простые сокращения числителя и знаменателя на 3 и на x, получим: — 1/5 y

Подставим значение y = 0,5: — 1 / (5 • 0,5) = — 1 / 2,5 = — 0,4

pазбирался: Даниил Романович | обсудить разбор | оценить

Найдите значение выражения:

при a = 13, b = 6,8

В данном случае, в отличие от первого, мы будем упрощать выражение вынося за скобки, а не раскрывая их.

Сразу можно заметить, что b присутствует у первой дроби в числителе, а у второй — в знаменателе, поэтому можем их сократить. Семь и четырнадцать тоже сокращаются на семь:

Далее выносим из числителя второй дроби a:

Подставляем значение a = 13:

pазбирался: Даниил Романович | обсудить разбор | оценить

Какое из данных ниже чисел является значением выражения?

Заметим, что в знаменателе присутствует разность (4 — √14), от которой нам необходимо избавиться. Как же это сделать?

Для этого вспоминаем формулу сокращенного умножения, а именно разность квадратов! Чтобы правильно её применить в этом задании необходимо помнить правила обращения с дробями. В данном случае вспоминаем, что дробь не изменяется, если числитель и знаменатель домножить на одно и то же число или выражение. Для разности квадратов нам не хватает выражения (4 + √14), значит, домножим на него числитель и знаменатель.

После этого в числителе получим 4 + √14, а в знаменателе разность квадратов: 4² — (√14)². После этого знаменатель легко вычисляется:

Суммарно наши действия выглядят так:

pазбирался: Даниил Романович | обсудить разбор | оценить

Аналогично предыдущим заданиям вычисляем знаменатель: для этого приводим дроби к общему знаменателю — это 84. Для этого первую дробь умножаем на 4, а вторую на 3, получим:

1/21 + 1/28 = 4/84 + 3/84

Итак, мы получили в знаменателе 7/84, теперь делим числитель на знаменатель — это все равно что умножить 1 на обратную 7/84 дробь:

1 / ( 7 / 84 ) = 1 •84/7 = 84/7

Далее остается поделить 84 на 7:

pазбирался: Даниил Романович | обсудить разбор | оценить

Можно решать задачу напрямую — вычисляя значения последовательно, это не должно составить труда, однако решение будет долгим и с большими вычислениями. Здесь можно заметить, что 1/3 присутствует как в уменьшаемом — 6 • (1/3)², так и в вычитаемом — 17 • 1/3, поэтому её можно легко вынести за скобку.

Проведя вычисления в скобках, получим:

1/3 • ( 6 • (1/3) — 17 ) = 1/3 • (6 /3 — 17 ) = 1/3 • ( 2 — 17 ) = 1/3 • ( -15 )

Теперь умножим полученное значение -15 на 1/3:

pазбирался: Даниил Романович | обсудить разбор | оценить