Функция « y = kx » и её график
Прежде чем перейти к изучению функции « y = kx » внимательно изучите урок
«Что такое функция в математике» и «Как решать задачи на функцию».
Функция « y = kx » — это первый тип функции, который изучается в математике.
Буквенный множитель « k » в функции « y = kx » называют числовым коэффициентом .
На месте « k » может стоять любое число (положительное, отрицательное или дробь).
Другими словами, можно сказать, что « y = kx » — это семейство всевозможных функций, где вместо « k » стоит число.
Примеры функций вида « y = kx ».
- y = 4x
- y = −1,5x
- y =
1 2 x
Давайте определим для каждой из функций выше, чему в них равен числовый коэффициент « k » .
Как построить график функции « y = kx »
Графиком функции « y = kx » является прямая .
Из геометрии вспомним аксиому (утверждение, которое не требует доказательства), что через любые две точки можно провести прямую и притом только одну.
Исходя из этой аксиомы, что чтобы построить график функции вида « у = kx » нам будет достаточно найти всего две точки.
Для примера построим график функции « y = −4x ».
Найдем значение функции « y » для двух произвольных значений « x ». Подставим, например, вместо « x » числа « 0 » и « 1 ».
Выбирая произвольные числовые значения вместо « x », лучше брать числа « 0 » и « 1 ». С этими числами легко выполнять расчеты.
| x | Расчет « y » |
|---|---|
| y(0) = −4 · 0 = 0 | |
| 1 | y(1) = −4 · 1 = −4 |
Полученные значения « x » и « y » — это координаты точек графика
функции « y = −4x ».
Запишем полученные координаты точек « y = −4x » в таблицу.
| Точка | Координата по оси « Оx » (абсцисса) | Координата по оси « Оy » (ордината) |
|---|---|---|
| (·)A | ||
| (·)B | 1 | −4 |
Отметим полученные точки на системе координат.
Теперь проведем прямую через отмеченные точки. Эта прямая и будет являться графиком функции « y = −4x ».
После построения не забудьте подписать график функции.
Как решать задачи на функцию « y = kx »
Построить график функции « y = −1,5x ». Найти по графику:
- значение « y » соответствующее значению « x » равному 1; 0; 2; 3 ;
- значение « x », если значение « y » равно −3; 4,5; 6 ;
- несколько целых значений « x », при которых значения « y » положительны (отрицательны).
Вначале построим график функции « y = −1,5x ».
Используем правила, по которым мы строили график функции выше. Для построения графика функции « y = −1,5x » достаточно найти всего две точки.
Выберем два произвольных числовых значения для « x ». Для удобства расчетов выберем числа « 0 » и « 1 ».
Выполним расчеты и запишем их результаты в таблицу.
| Точка | Координата по оси « Оx » | Координата по оси « Оy » |
|---|---|---|
| (·)A | y(0) = −1,5 · 0 = 0 | |
| (·)B | 1 | y(1) = −1,5 · 1 = −1,5 |
Отметим полученные точки на прямоугольной системе координат.
Соединим полученные точки прямой. Проведенная прямая будет являться графиком функции « y = −1,5x ».
Теперь работаем с построенным графиком функции « y = −1,5x ».
Требуется найти значение « y », соответствующее значению « x » равному 1; 0; 2; 3 .
Тему «Как получить координаты точки функции» с графика функции мы уже подробно рассматривали в уроке «Как решать задачи на функцию».
В этому уроке для решения задачи выше вспомним только основные моменты.
Чтобы найти значение « y » по известному значению « x » на графике функции необходимо:
- провести перпендикуляр от оси « Ox » (ось абсцисс) из заданного числового значения « x » до пересечения с графиком функции;
- из полученной точки пересечения перпендикуляра и графика функции провести еще один перпендикуляр к оси « Oy » (ось ординат);
- полученное числовое значение на оси « Oy » и будет искомым значением.
По правилам выше найдем на построенном ранее графике функции « y = −1,5x » необходимые значения функции « y » для « x » равным 1; 0; 2; 3 .
Запишем полученные результаты в таблицу.
| Заданное значение « x » | Полученное с графика значение « y » |
|---|---|
| 1 | −1,5 |
| 2 | −3 |
| 3 | −4,5 |
Переходим ко второму заданию задачи. Требуется найти значение « x », если значение « y » равно −3; 4,5; 6 .
Выполним те же действия, что и при решении предыдущего задания. Разница будет лишь в том, что изначально мы будем проводить перпендикуляры
от оси « Oy ».
Запишем полученные результаты в таблицу.
| Заданное значение « y » | Полученное с графика значение « x » |
|---|---|
| −3 | 2 |
| 4,5 | −3 |
| 6 | −4 |
Перейдем к последнему заданию. Нас просят найти несколько целых значений « x », при которых значения « y » положительны (отрицательны).
Для решения этой задачи необходимо внимательно изучить
график функции « y = −1,5x ».
Отметим область на оси « Oy », где значения « y » для графика функции « y = −1,5x » положительны.
Из этой области проведем от графика функции несколько перпендикуляров к оси « Ox » .
Помните, что по заданию, нас просят найти несколько «целых» значений « x ». Поэтому перпендикуляры мы будем проводить к оси « Ox » в целые числовые значения.
Запишем ответ. При x = −2; x = −1 значения y > 0 .
Теперь найдем при каких « x », значения « y » отрицательны. Отметим область на оси « Oy », где значения « y » на графике функции отрицательны.
Проведем перпендикуляры из отмеченной области к оси « Ox » в целые числовые значения « x ».
Запишем ответ. При x = 1; x = 2 значения y .
Рассмотрим другую задачу.
Какие из точек A(5; −3) , D(2; 1) принадлежат графику функции, заданной
формулой « y =
| 1 |
| 2 |
x »?
Подробный разбор задачи «Как проверить, что точка принадлежит графику функции» мы приводили в уроке «Как решать задачи на функцию».
В этом уроке мы вспомним только основные моменты решения подобных задач.
Чтобы проверить принадлежность точки графику функции нет необходимости строить график функции.
Достаточно подставить координаты точки в формулу функции (координату по оси « Ox » вместо « x », а координату по оси « Oy » вместо « y ») и выполнить арифметические расчеты.
- Если получится верное равенство, значит точка принадлежит графику функции.
- Если получится не верное равенство, значит точка не принадлежит графику функции.
Функция y=k/x и ее график
Урок 8. Алгебра 8 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока “Функция y=k/x и ее график”
Давайте рассмотрим пример:
Пусть расстояние в 200 км автомобиль со скоростью равной v км/ч преодолеет за время равное t часов. Тогда используя формулу пути, зависимость времени от скорости движения автомобиля при равном расстоянии можно выразить формулой:
Напомню, что такую зависимость называют обратно пропорциональной. Т.к. при увеличении одной величины вторая величина будет уменьшаться.
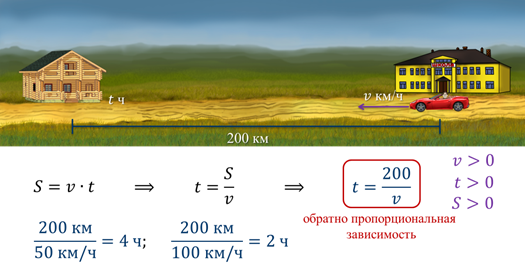
Вот, например, если автомобиль будет ехать со скоростью 50 км/ч, то на преодоление расстояния в 200 км ему понадобится 4 часа.
А вот, если автомобиль будет ехать со скоростью 100 км/ч, то на преодоление этого же пути, ему понадобится всего лишь 2 часа. Видим, что при увеличении скорости, времени тратится меньше.
Но в этой задаче переменные v и t могут принимать лишь положительные значения, т.к. скорость, время и расстояние это положительные величины.
В дальнейшем мы будем рассматривать функции, задаваемые формулой вида:
Такие функции называют обратными пропорциональностями.
С обратной пропорциональностью мы с вами часто встречаемся в повседневной жизни.
Масса m кг конфет, которую можно купить на 1 000 рублей по цене p рублей за кг. Зависимость массы конфет от стоимости за килограмм является обратно пропорциональной. Или, если есть прямоугольник длина которого a см, а ширина b см с площадью равной 27 см 2 . Такая зависимость также является обратно пропорциональной.
Определение:
Обратной пропорциональностью называется функция, которую можно задать формулой вида:
где x – независимая переменная и k – не равное 0 число.
Число k – называют коэффициентом обратной пропорциональности.
В нашем примере
Областью определения функции, заданной формулой вида:
является множество действительных чисел, отличных от нуля, т.к. выражение 
имеет смысл при любых x, кроме x равное нулю.
Теперь давайте построим график обратной пропорциональности 
.
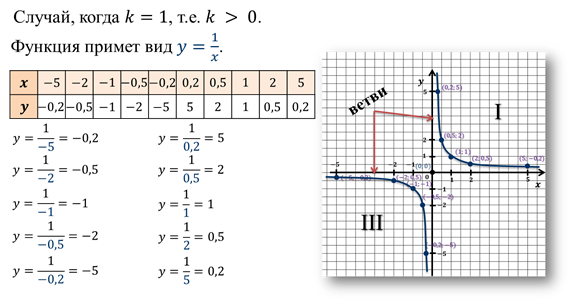
Полученный график состоит из двух симметричных относительно начала координат частей. Их обычно называют ветвями. Одна из этих ветвей расположена в первой четверти, вторая – в третьей.
График функции при любом k > 0 имеет такой же вид, что и график функции 
.
Теперь построим график функции . 
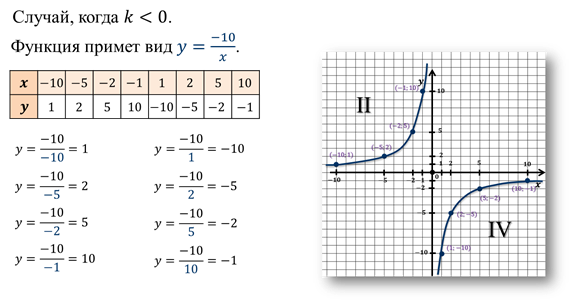
Такой же вид имеет график функции при любом k 0 ветви гиперболы лежат в 1-ой и 3-ей четвертях. При k Оцените видеоурок
График линейной функции, его свойства и формулы
О чем эта статья:
Понятие функции
Функция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
- Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ — наглядно.
- Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.
Понятие линейной функции
Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.
Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.
Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.
Если известно конкретное значение х, можно вычислить соответствующее значение у.
Нам дана функция: у = 0,5х – 2. Значит:
- если х = 0, то у = -2;
- если х = 2, то у = -1;
- если х = 4, то у = 0;
- и т. д.
Для удобства результаты можно оформлять в виде таблицы:
| х | 2 | 4 | |
| y | -2 | -1 |
Графиком линейной функции является прямая линия. Для его построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.
Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.
Буквенные множители «k» и «b» — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.
Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты «k» и «b».
| Функция | Коэффициент «k» | Коэффициент «b» |
|---|---|---|
| y = 2x + 8 | k = 2 | b = 8 |
| y = −x + 3 | k = −1 | b = 3 |
| y = 1/8x − 1 | k = 1/8 | b = −1 |
| y = 0,2x | k = 0,2 | b = 0 |
Может показаться, что в функции «y = 0,2x» нет числового коэффициента «b», но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа «y = kx + b» есть коэффициенты «k» и «b».
Свойства линейной функции
- Область определения функции — множество всех действительных чисел.
- Множеством значений функции является множество всех действительных чисел.
- График линейной функции — прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.
- Функция не имеет ни наибольшего, ни наименьшего значений.
- Четность и нечетность линейной функции зависят от значений коэффициентов k и b:
b ≠ 0, k = 0, значит y = b — четная;
b = 0, k ≠ 0, значит y = kx — нечетная;
b ≠ 0, k ≠ 0, значит y = kx + b — функция общего вида;
b = 0, k = 0, значит y = 0 — как четная, так и нечетная функция. - Свойством периодичности линейная функция не обладает, потому что ее спектр непрерывен.
- График функции пересекает оси координат:
ось абсцисс ОХ — в точке (-b/k, 0);
ось ординат OY — в точке (0; b). - x=-b/k — является нулем функции.
- Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.
Если b ≠ 0 и k = 0, то функция y = b не обращается в нуль ни при каких значениях переменной х. - Функция монотонно возрастает на области определения при k > 0 и монотонно убывает при k 0: функция принимает отрицательные значения на промежутке (-∞, – b /k) и положительные значения на промежутке (- b /k, +∞)
При k b /k, +∞) и положительные значения на промежутке (-∞, – b /k). - Коэффициент k характеризует угол, который образует прямая с положительным направлением Ох. Поэтому k называют угловым коэффициентом.
Если k > 0, то этот угол острый, если k
Построение линейной функции
В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида «у = kx + b», достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.
Например, чтобы построить график функции y = 1 /3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:
В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
- если k > 0, то график наклонен вправо;
- если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;
- если b 1 /2x + 3, y = x + 3.
Проанализируем рисунок. Все графики наклонены вправо, потому что во всех функциях коэффициент k больше нуля. Причем, чем больше значение k, тем круче идет прямая.
В каждой функции b = 3, поэтому все графики пересекают ось OY в точке (0; 3).
Теперь рассмотрим графики функций y = -2x + 3, y = – 1 /2x + 3, y = -x + 3.
В этот раз во всех функциях коэффициент k меньше нуля, и графики функций наклонены влево. Чем больше k, тем круче идет прямая.
Коэффициент b равен трем, и графики также пересекают ось OY в точке (0; 3).
Рассмотрим графики функций y = 2x + 3, y = 2x, y = 2x – 2.
Теперь во всех уравнениях функций коэффициенты k равны. Получили три параллельные прямые.
При этом коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
- график функции y = 2x + 3 (b = 3) пересекает ось OY в точке (0; 3);
- график функции y = 2x (b = 0) пересекает ось OY в точке начала координат (0; 0);
- график функции y = 2x – 2 (b = -2) пересекает ось OY в точке (0; -2).
Прямые будут параллельными тогда, когда у них совпадают угловые коэффициенты.
Подытожим. Если мы знаем знаки коэффициентов k и b, то можем представить, как выглядит график функции y = kx + b.
Если k 0, то график функции y = kx + b выглядит так:
0″ src=”https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png” style=”height: 600px;”>
Если k > 0 и b > 0, то график функции y = kx + b выглядит так:
0 и b > 0″ src=”https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png” style=”height: 600px;”>
Точки пересечения графика функции y = kx + b с осями координат:
- С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.
Координаты точки пересечения с осью OY: (0; b). - С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = – b /k.
Координаты точки пересечения с осью OX: (- b /k; 0)
Решение задач на линейную функцию
Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!
Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.
- В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.
Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.
Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:
2 = -4(-3) + b
b = -10 - Таким образом, нам надо построить график функции y = -4x – 10
Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).
Поставим эти точки в координатной плоскости и соединим прямой:
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
- Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.
Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство. - Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.
- Вычтем из второго уравнения системы первое, и получим k = 3.
Подставим значение k в первое уравнение системы, и получим b = -2.
Конспект урока алгебры по теме: “Функция y = k/x, её свойства и график”
Разделы: Математика
Цель:
-
ввести понятие функции y=k/x как обратно пропорциональную зависимость, через рассмотрение свойств данной функции и построение графика.
1. Самоопределение учебной деятельности
Цель этапа:
- включить учащихся в учебную деятельность;
- определить содержательные рамки урока: продолжить изучать степенную функцию.
Организация учебного процесса на этапе 1:
– Какую главу мы начали изучать на прошлых уроках? (Степенная функция)
– Сегодня мы продолжим работать над этой темой.
2. Актуализация знаний и фиксация затруднений в деятельности
Цель этапа: актуализировать учебное содержание, необходимое и достаточное для восприятия нового материала: свойства и графики функций, известных учащимся с 7-го класса;
Организация учебного процесса на этапе 2:
1. Укажите области определения следующих функций: y=x 2 +8, y=1/x-7, y=4x-1/5 y=2x, y=7-5x, y=2/x, y=x 3 , y= -10/x
2. На каком рисунке из таблицы (приложение 1) изображен график:
– линейной функции;
– прямой пропорциональности;
– квадратичной функции;
– функции вида y=kx 3
3. Какой знак имеет коэффициент k в формулах вида y=kx+b, которым соответствуют графики на рисунке 1, 2, 4, 5 таблицы?
4. Найдите в таблице графики линейных функций, у которых угловые коэффициенты: равны; равны по модулю и противоположны по знаку.
5. Как называются следующие функции, заданные формулами: y=kx 2 , y=x 2 , y=kx 2 , y=x 3 , y=kx 3 ,y=kx+b, y=k/x?
3. Выявление причины затруднения и постановка цели деятельности
Цель этапа: организовать коммуникативное воздействие, в ходе которого выявляется и фиксируется отличительное свойство задания, вызвавшего затруднения в учебной деятельности;
согласовать цель и тему урока.
Организация учебного процесса на этапе 3:
– Почему это задание вызвало затруднение? (Незнакомы с данной функцией).
– Какова цель урока? (Познакомиться с функцией y=k/x, ее свойствами и графиком.)
– Записываем число, классная работа и тему урока: “Функция y=k/x, ее свойства и график”.
4. Построение проекта выхода из затруднения
Цель этапа:
- организовать коммуникативное взаимодействие для построения нового способа действия, устраняющего причину выявленного затруднения;
- зафиксировать новый способ действия в знаковой, вербальной форме и с помощью эталона.
Организация учебного процесса на этапе 4:
– Работа в группах по алгоритму:
- Заполнить таблицу значений x и y для предложенной функции (каждой группе индивидуальное задание: y=5/x, y= -5/x, y=8/x, y= -8/x).
- По данным в таблице координатам (x;y) построить на координатной плоскости соответствующие точки.
- Ответить на вопросы:
– какова область определения заданной функции? (x не равно 0);
– принадлежит ли точка (0;0) графику функции? (Не принадлежит);
– пересекает ли график функции оси OY и OX? (Не пересекает).
– соединить точки и получить график целиком;
– подготовить отчет о проделанной работе.
– Сравните полученные графики (они симметричны относительно начала координат).
– Как зависит расположение графика от знака коэффициента k? (Если k>0, то график расположен в I и III координатных углах, а если k
| x | – 6 | – 4 | – 3 | – 2 | 1 | 2 | 3 | 4 | 6 |
| y | + 1 | +1,5 | + 2 | + 3 | – 6 | – 3 | – 2 | – 1,5 | – 1 |
Постройте график обратной пропорциональности y=16/x, предварительно заполнив таблицу
| x | – 8 | – 4 | – 2 | – 1 | 1 | 2 | 4 | 8 |
| y |
Постройте таблицу некоторых значений функции y=10/x и ее график.
– Работы проверяются по эталону. Ошибки исправляются, анализируются, выясняется их причина.
6. Рефлексия деятельности
Цель этапа: зафиксировать новое содержание, изученное на уроке;
Организация учебного процесса на этапе 6:
– Что нового узнали на уроке?
– Что использовали для “открытия” нового знания?
– Какие трудности встретили?
– Что нам помогло справиться с затруднениями?
Гипербола. График функции и свойства.
теория по математике функции
Графиком функции у= k x . . , где k ≠ 0 число, а х – переменная, является кривая, которую называют гиперболой.
Гипербола имеет две ветви и может располагаться в 1 и 3 координатных четвертях, либо во 2 и 4. Это зависит от знака числа k. Рассмотрим данную кривую на рисунке, где показано ее расположение в зависимости от знака k.
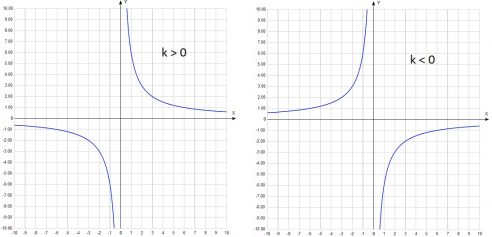
Свойства гиперболы (у= k x . )
График функции симметричен относительно начала координат (0;0). Поэтому функцию еще называют – обратная пропорциональность.
- Область определения – любое число, кроме нуля.
- Область значения – любое число, кроме нуля.
- Функция не имеет наибольших или наименьших значений.
Построение графика функции
Для построения графика функции необходимо подбирать несколько положительных и несколько отрицательных значений переменной х, затем подставлять их в заданную функцию для вычисления значений у. После этого по найденным координатам построить точки и соединить их плавной линией. Рассмотрим построение графиков на примерах.
Построить график функции у= 10 x . . .
Для этого построим две таблицы для положительных и отрицательных значений х. Подбирать желательно такие значения х, чтобы число 10 на них делилось
| х | 1 | 2 | 4 | 5 | 10 |
| у |
| х | –1 | –2 | –4 | –5 | –10 |
| у |
Теперь делим на эти числа 10, получим значения у:
| х | 1 | 2 | 4 | 5 | 10 |
| у | 10 | 5 | 2,5 | 2 | 1 |
| х | –1 | –2 | –4 | –5 | –10 |
| у | –10 | –5 | –2,5 | –2 | –1 |
Выполняем построение точек, они будут располагаться в первой и третьей координатных четвертях, так как число k положительное.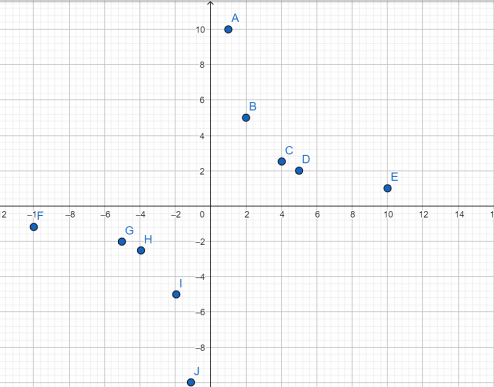 
Теперь для построения гиперболы соединим точки плавной линией.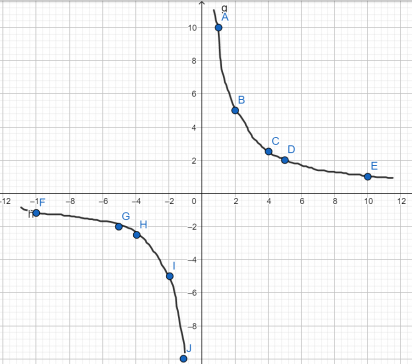 
Построить график функции у= − 5 x . . .
Для этого построим также две таблицы для положительных и отрицательных значений х. Подбирать желательно такие значения х, чтобы число минус 5 на них делилось. Выполняем деление и получаем значения у. При делении обращаем внимание на знаки, чтобы не допускать ошибок.
| х | 1 | 2 | 5 | 10 |
| у | –5 | –2,5 | –1 | –0,5 |
| х | –1 | –2 | –5 | –10 |
| у | 5 | 2,5 | 1 | 0,5 |
Теперь отмечаем точки во 2 и 4 координатных четвертях (число k отрицательное) и соединяем их для получения ветвей гиперболы.
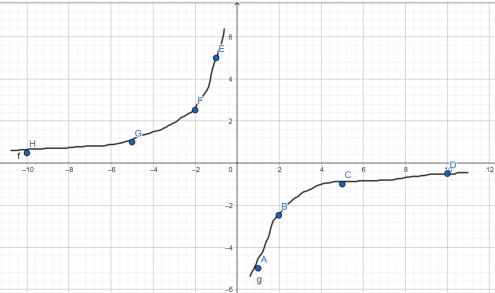
Установите соответствие между графиками функций и формулами, которые их задают.
1) y = x²
Для решения данной задачи необходимо знать вид графиков функций, а именно:
y = x² — парабола, в общем виде это y = ax²+bx+c, но в нашем случае b = c = 0, а а = 1
x/2 — прямая, в общем виде график прямой имеет вид y = ax + b, в нашем случае b = 0, а = 1/2
y = 2/x — гипербола, в общем виде график функции y = a/x + b, в данном примере b = 0, a = 2
Парабола изображена на рисунке А, гипербола на рисунке Б, а прямая — В.
pазбирался: Даниил Романович | обсудить разбор | оценить
Установите соответствие между функциями и их графиками.
В данной ситуации можно воспользоваться двумя подходами — можно руководствоваться общими соображениями, а можно просто решить задачу подстановкой. Я рекомендую решать задачу общими соображениями, а проверять подстановкой.
- если уравнение гиперболы положительное (то есть не стоит знак -, как во втором и третьем случае), то график функции лежит в первой и третьей координатной четверти
- если перед уравнением гиперболы стоит знак — (как в первом случае), то график лежит во второй и четвертой четвертях
Таким образом можно сразу определить, что первое уравнение соответствует графику под номером 2.
Второе правило, которым я пользуюсь, звучит так:
- чем больше число в знаменателе гиперболы (рядом с x), тем сильнее гипербола жмется к осям координатной плоскости
- чем больше число в числителе уравнения гиперболы, тем слабее и медленнее график функции прижимается к осям
Следовательно, функция Б слабее прижимается к осям и ей соответствует график 3, а функции В соответствует график 1, так как она сильнее прижимается к осям.
pазбирался: Даниил Романович | обсудить разбор | оценить
Урок “Свойства функции y=k/x, при k меньше 0”
Краткое описание документа:
Данный видеоурок по курсу математики познакомит вас со свойствами функции y = k/x, при условии, что значение k будет отрицательным.
В наших предыдущих видеоуроках вы познакомились с самой функцией y равно k деленное на x, ее графиком, который называется «гипербола», а также свойствами графика при положительном значении k. Данное видео познакомит вас со свойствами коэффициента k при отрицательном его значении, то есть меньше нуля.
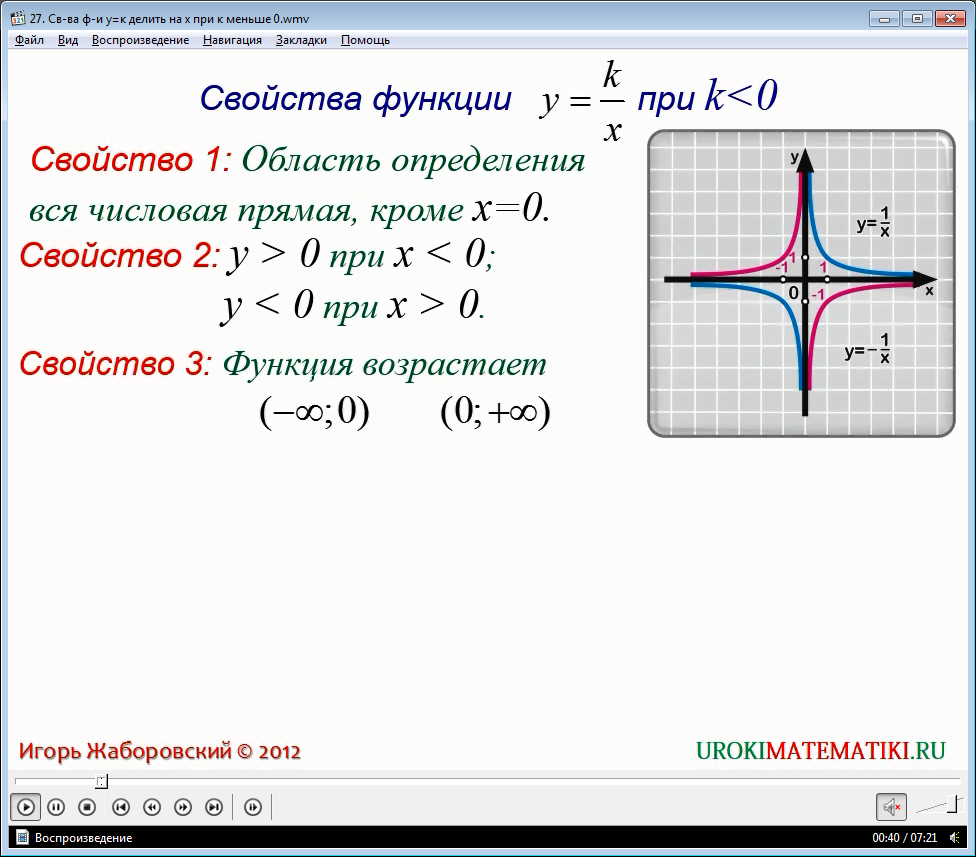
Свойства равенства, при котором y равняется коэффициенту k, деленному на независимую переменную x, при условии, что коэффициент имеет отрицательное значение, представлены в видеоматериале.
При описании свойств этой функции, прежде всего, опираются на ее геометрическую модель – гиперболу.
Свойство 1. Область определения функции состоит из всех чисел, однако следует, что x не может равняться 0, потому что на ноль делить нельзя.
Свойство 2. у больше нуля при условии, что х меньше нуля; и, соответственно, наоборот, у меньше нуля при значении, когда х находится в пределах больше нуля и до бесконечности.
Свойство 3. Функция возрастает на промежутках от минус бесконечности до нуля и от нуля до плюс бесконечности: (-∞, 0) и (0, +∞).
Свойство 4. Функция является бесконечной, так как не имеет ограничений ни снизу, ни сверху.
Свойство 5. Ни наименьшего, ни наибольшего значений у функции нет, поскольку она бесконечна.
Свойство 6. Функция является непрерывной на промежутках от минус бесконечности до нуля (-∞, 0) и от нуля до бесконечности (0, +∞), при этом следует обозначить, что она претерпевает разрыв в том случае, когда х имеет значение ноль.
Свойство 7. Область значений функций является объединением двух открытых лучей от минус бесконечности до нуля (-∞, 0) и от нуля до плюс бесконечности (0, +∞).
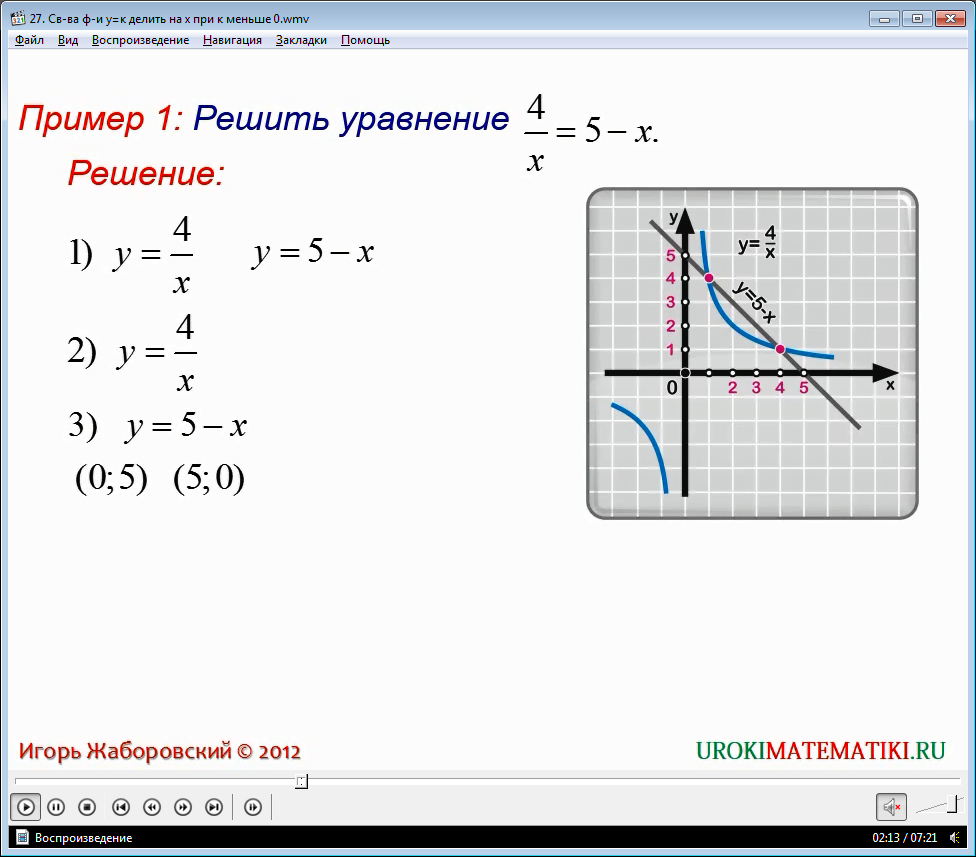
Далее в видео приводятся примеры. Мы рассмотрим только некоторые из них, остальные рекомендуем посмотреть самостоятельно в предоставленных видеоматериалах.
Итак, рассмотрим первый пример. Необходимо решить уравнение следующего вида: 4/x = 5-x.
Для большего удобства разделим решение данного равенства на несколько этапов:
1) Для начала записываем наше равенство в виде двух отдельных уравнений: y = 4/x и y = 5-x/
2) Затем, как показано в видео, строим график функции y = 4/x, который является гиперболой.
3) Далее строим график линейной функции. В данном случае это прямая, которую можно построить по двум точкам. Графики представлены в нашем видеоматериале.
4) Уже по самому чертежу определяем точки, в которых пересекаются оба наших графика, и гипербола, и прямая. Следует обозначить, что они пересекаются в точках А (1; 4) и В (4; 1). Проверка полученных результатов показывает, что они верны. Данное уравнение может иметь два корня 1 и 4.
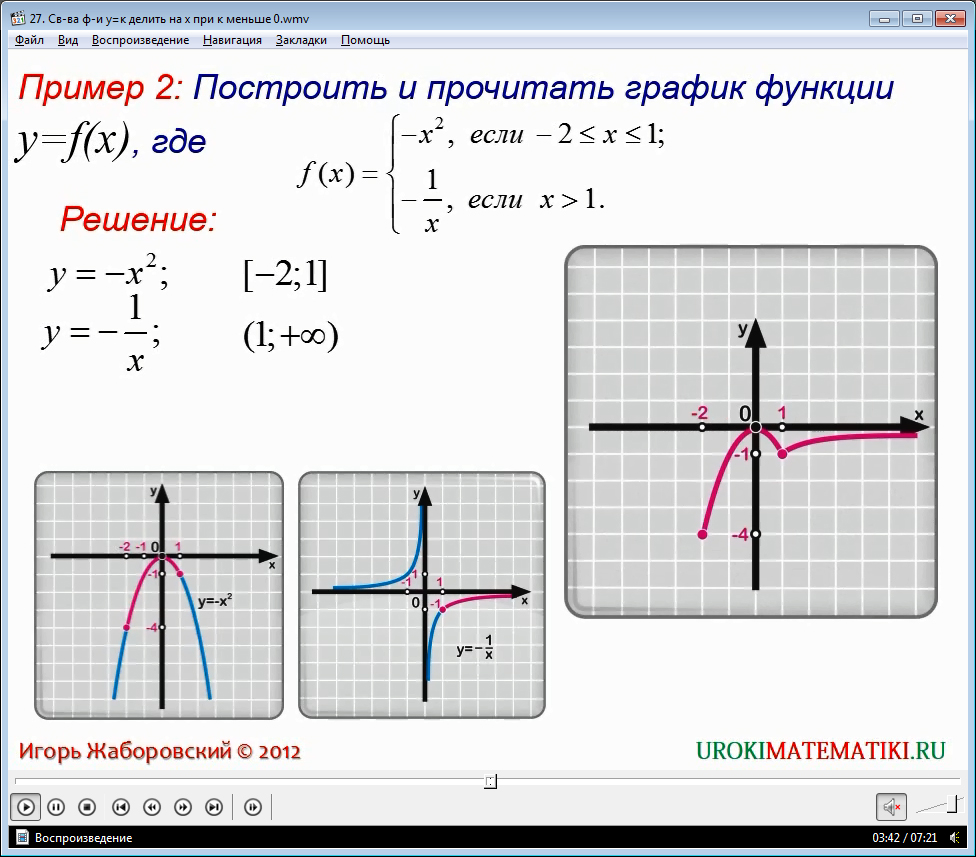
Следующий пример, рассмотренный в видеоуроке, имеет следующее задание: построить и прочитать график функции у = f(x), где f(x) = -x2, в случае если переменная x находится в пределах от больше или равно -2 и до больше или равно 1, и y = -1/x, в случае если x больше единицы.
Решение проводим в несколько этапов. Сначала строим график функции y = -x2, который называется «парабола», и выделяем ее часть на участке от – 2 до 1. Для просмотра графика обратитесь к видео.
Следующим этапом является построение гиперболы для равенства y = -1/x, и выделяем ее часть на открытом луче от единицы до бесконечности. Далее производим смещение обоих графиков в одной системе координат. В результате мы получаем график функции у = f(x).
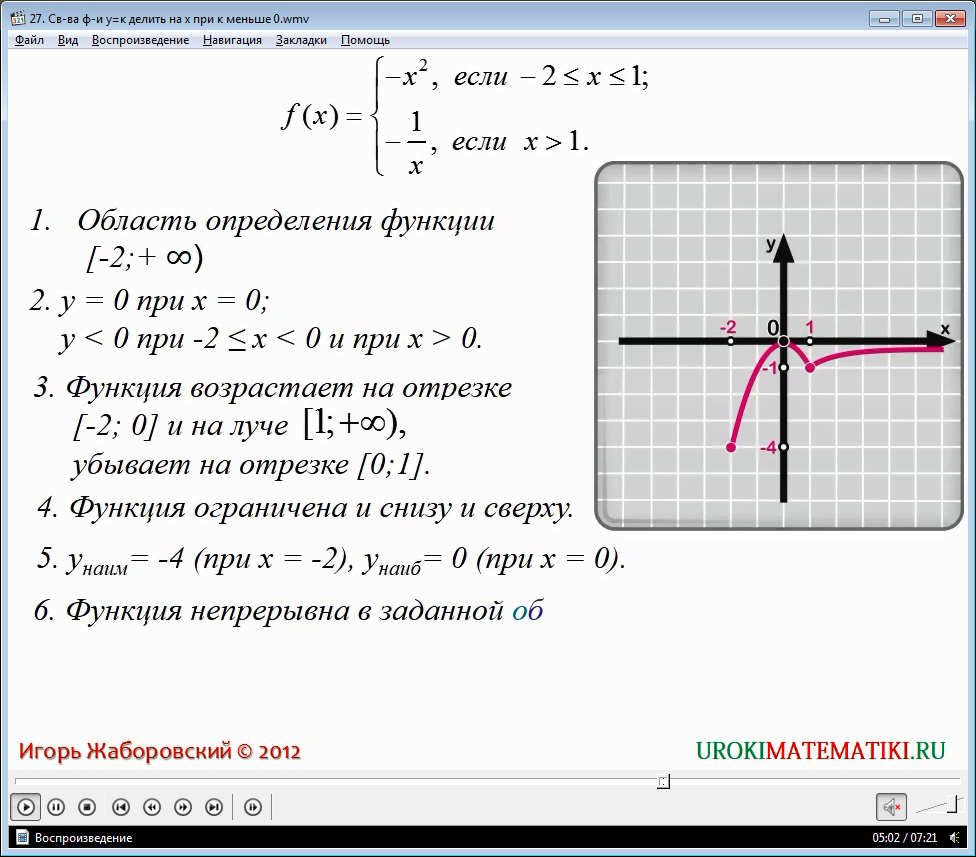
Далее следует прочитать график функции у = f(x):
1. Область определения функции – это луч на участке от -2 до +∞.
2. у равняется нулю в том случае, когда х равняется нулю; у меньше нуля при значении x больше или равно -2 и меньше нуля, а также при x больше нуля.
3. Функция возрастает на участке от -2 до 0 и на участке от 1 и до бесконечности, график показывает убывание на отрезке от нуля до единицы.
4. Функция с заданными параметрами является ограниченной как снизу, так и сверху.
5. Наименьшее значение переменной y равняется – 4 и постигается при значении х на уровне – 2; и также наибольшим значением y является 0, который достигается при значении х равному нулю.
6. В заданной области определения наша функция является непрерывной.
7. Область значения функции располагается на отрезке от -4 до 0.
8. Функция выпукла вверх на отрезке от -2 до 1 и на луче от 1 до бесконечности.
С оставшимися примерами вы сможете ознакомиться самостоятельно, просмотрев представленное видео.
Конспект урока по алгебре: «Функция у = k/x, её свойства и график»
Цели урока : сформулировать определение обратной пропорциональности, её области определения и графика.
Задачи урока :
Обучающая: повторить понятие функции, их виды и графики, научить находить значение функции и аргумента по формуле у = k/x , строить график обратной пропорциональности и «читать» его.
Развивающая: продолжить развитие познавательного интереса к изучению алгебры; развивать умение анализировать, наблюдать, сопоставлять, логически мыслить; продолжить развитие элементов творческой деятельности учащихся, через вовлечение их в работу частично поискового характера, развитие навыков взаимоконтроля и самоконтроля.
Воспитывающая: воспитание умения слушать и слышать другого, уважение к мнению товарища; воспитание у учащихся таких нравственных качеств, как настойчивость, аккуратность, инициативность, точность, привычка к систематичному труду, самостоятельность, активность; воспитание культуры общения.
Формы работы: индивидуальная, фронтальная.
Оборудование: п ерсональный компьютер, мультимедийный проектор, экран, а вторская презентация , к арточки с заданиями, учебник «Алгебра» 8 класс, Ю.Н., Миндюк Н.Г. и др.
Ход урока :
Организационный момент(1 мин)
Сегодня на уроке мы с вами повторим основные понятия по теме «Функция», познакомимся с функцией обратной пропорциональности, научимся строить ее график. Дома вы выполняли задания на упрощение выражений. Какие у вас вопросы по домашнему заданию. Если у вас нет вопросов, то давайте поработаем устно.
II . Устная работа(5 мин)
1. Проверить устно, правильно ли выполнены действия. Ели нет, скажите верный ответ.
2. Сократите дробь :
3. Как называется данная функция, указать ООФ и что представляет собой их график.
y = 2 x + 3, (Линейная функция, ООФ: х- л.ч., График: прямая)
y = x 2 , (Квадратичная функция, ООФ: х- л.ч., График: парабола)
y = x 3. (Кубическая функция, ООФ: х- л.ч., График: кубическая парабола)
y = 2 x , (Прямая пропорциональность, ООФ: х-л.ч., График: прямая, проходящая через начало координат)
III . Подготовка к изучению нового материала.(3 мин)
(Записываем в тетрадь число(14.10.11), классная работа)(Функция у = k/x, ее свойства и график )
Нам известно, что каждая из данных функций описывает какие- то процессы, происходящие в окружающем нас мире. Давайте рассмотрим следующую задачу:
Дан прямоугольник со сторонами 2 и x. Как найти площадь данного прямоугольника? ( S =2х). Что будет происходить с площадью, если неизвестную сторону х увеличить в 2 раза? Как называется данная зависимость?(Функция), где х – независимая переменная, а S – зависимая переменная. Как называется данная функция? (Прямая пропорциональность)
А теперь другая задача: Дан прямоугольник со сторонами x, y и площадью равной 8 кв. единицам. Запишите формулу площади прямоугольника? (Спросить у детей, кто что написал.) (x y=8)
Если мы с вами увеличим одну сторону в 2 раза, что произойдет с другой стороной, при условии, что площадь останется той же? (Ответ детей)
А теперь эту сторону уменьшить в два раза?
Какой же можно сделать вывод?
Я Вывод: что при увеличении одной переменной в несколько раз вторая переменная уменьшается во столько же раз. И наоборот, при уменьшении одной переменной в несколько раз вторая переменная увеличивается во столько же раз. Выразим переменную у через х. y= 8/x.
8 – число, заменим его на к . Получим
Такую зависимость переменных можно назвать обратной пропорциональностью. Как вы думаете, может ли к равняться нулю? (Может, тогда подставим. Получаем у=0, а это есть ось абсцисс) Что такое х? А какие значения она может принимать? А может ли х = нулю. ООФ? А у? (Нет, так как к ≠0 и х ≠0)А что такое у?
IV. Объяснение нового материала.(10 мин)
Обратной пропорциональностью называется функция, которую можно задавать формулой вида у = , где х – независимая переменная и k – не равное нулю число.
Приведите примеры обратно пропорциональной функции. (Записать две-три.) Чтобы было отрицательное число
Давайте построим графики функции у =6/х и у = – 6/х.
I вариант будет строить график функции у = 6/х , а II – у = – 6/х.
Но для начала найдем ООФ. Что такое ООФ?
(ООФ: х ООФ – множество всех чисел, отличных от нуля)
Для построения графика нам необходимо заполнить таблицы: по вариантам и нанести полученные точки на координатную плоскость.
Один ученик из каждого варианта (а остальные в тетрадях) заполняют таблицу значений функции на доске.
Следующий этап – это построения на координатной плоскости. Наносим получившиеся точки на координатную плоскость. Проверяем!
Соединяем данные точки плавными линиями.
– В каких координатных четвертях расположен график?
– Как вы думаете, отчего зависит расположение графика?
График не пересекает оси координат, так как ни х, ни у не могут равняться нулю.
После построения функций у =6/х и у = – 6/х. Мы можем сделать выводы, что
График не пересекает ни ось абсцисс, ни ось ординат;
2. График расположен в I и III координатных четвертях если к > 0 (y= 6/x) и во II и IV , если к
Полученная кривая называется гиперболой (записать в тетрадь). Она состоит из двух ветвей.
Ученик. Гипербола в переводе с греческого языка дословно означает «прохожу через что-либо» и с течением времени получило второе смысловое значение «преувеличение». Одним из первых, кто начал изучать эту кривую был ученик знаменитого Платона, древнегреческий математик Менехм в IV в. до н.э., но так и не сумел её полностью изучить.
А вот полностью исследовал свойства гиперболы и дал ей название крупнейший геометр древности Аполоний Пергский в III в. до н.э.
На свойство гиперболы к преувеличению или к преуменьшению обратили внимание поэты и писатели. Так в словаре русского языка Ожегова слово гипербола трактуется как поэтический приём чрезмерного преувеличения с целью усиления впечатления.
Русский поэт Николай Алексеевич Некрасов тоже любил этот прием и применял его в своих стихах. Например: Пройдёт – словно солнцем осветит: Посмотрит – рублём подарит! … Я видывал, как она косит: Что взмах – то готова копна. )
После столь лирического отступления давайте проверим на сколько вы усвоили тему.
Открываем учебник на 41 странице и читаем определение, обратной пропорциональности.
V. Закрепление материала (13 мин)
а) х = 2 у = 4 б) у = -4 х = -2
х = 4 у = 2 у = -2 х = -4
х = -1 у = – 8 у = 8 х = 1.
Дополнит. номер (Устно)
Обратная пропорциональность задана формулой у = .
Принадлежат ли точки А(3; 5) , В(5; -3), С( ; 20) графику этой функции?
2) Функция задана формулой у = – . Найти:
а) значения функции, если значение аргумента равно -3; 6; 0,5;
б) значение аргумента, при котором значение функции равно 12;
у = ; х=2, у = 12. (ученик)
Найти значение к.
V I . Самостоятельная работа (7 мин)
А теперь давайте проверим каждый сам себя, на сколько он усвоил принцип построения графика функции обратной пропорциональности у = к/х.
У вас на столе лежат карточки с заданиями по вариантам.
Вам нужно заполнить таблицу, построить график соответствующей функции. Проверить, принадлежит ли данная точка графику функции?
