Дифракционная решетка формулы, период, виды дифракции света

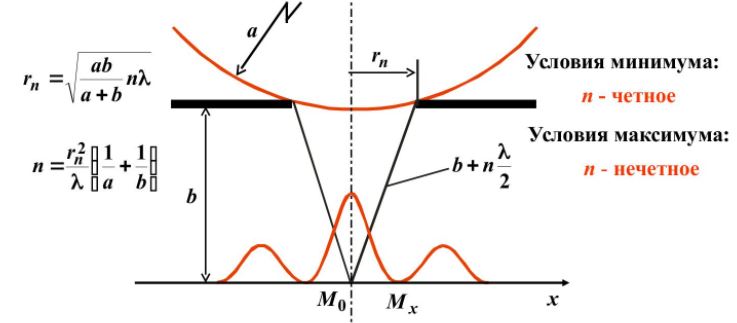
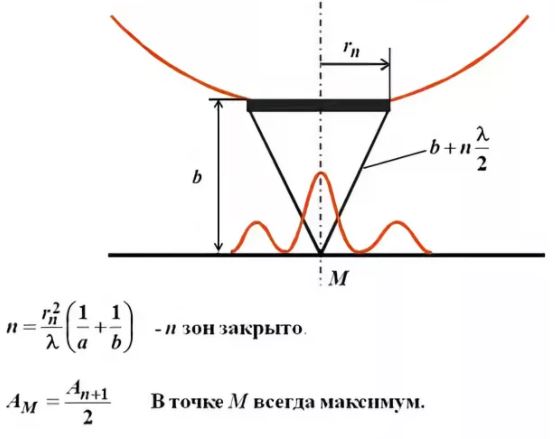
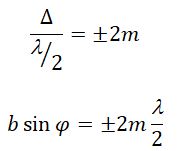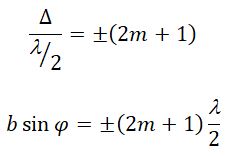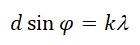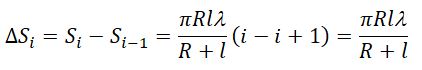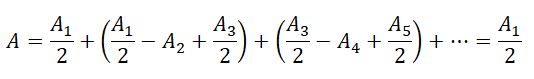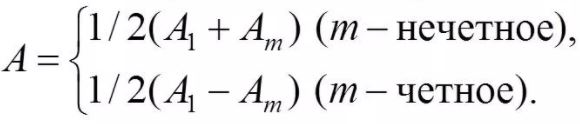Основная формула дифракционной решетки

В чем заключаются явления дифракции и интерференции?

Прежде чем рассматривать вывод формулы дифракционной решетки, следует познакомиться с явлениями, благодаря которым это решетка оказывается полезной, то есть с дифракцией и интерференцией.

Дифракция — это процесс изменения движения волнового фронта, когда на своем пути он встречает непрозрачное препятствие, размеры которого сравнимы с длиной волны. Например, если через маленькое отверстие пропустить солнечный свет, то на стене можно наблюдать не маленькую светящуюся точку (что должно было произойти, если бы свет распространялся по прямой линии), а светящееся пятно некоторых размеров. Этот факт свидетельствует о волновой природе света.

Интерференция — еще одно явление, которое характерно исключительно для волн. Его суть заключается в наложении волн друг на друга. Если волновые колебания от нескольких источников согласованы (являются когерентными), тогда можно наблюдать устойчивую картину из чередующихся светлых и темных областей на экране. Минимумы на такой картине объясняются приходом волн в данную точку в противофазе (pi и -pi), а максимумы являются результатом попадания в рассматриваемую точку волн в одной фазе (pi и pi).

Оба описанных явления впервые объяснил англичанин Томас Юнг, когда исследовал дифракцию монохроматического света на двух тонких щелях в 1801 году.

Принцип Гюйгенса-Френеля и приближения дальнего и ближнего полей

Математическое описание явлений дифракции и интерференции является нетривиальной задачей. Нахождение точного ее решения требует выполнение сложных расчетов с привлечением максвелловской теории электромагнитных волн. Тем не менее в 20-е годы XIX века француз Огюстен Френель показал, что, используя представления Гюйгенса о вторичных источниках волн, можно с успехом описывать эти явления. Эта идея привела к формулировке принципа Гюйгенса-Френеля, который в настоящее время лежит в основе вывода всех формул для дифракции на препятствиях произвольной формы.

Тем не менее даже с помощью принципа Гюйгенса-Френеля решить задачу дифракции в общем виде не удается, поэтому при получении формул прибегают к некоторым приближениям. Главным из них является плоский волновой фронт. Именно такая форма волны должна падать на препятствие, чтобы можно было упростить ряд математических выкладок.

Следующее приближение заключается в положении экрана, куда проецируется дифракционная картина, относительно препятствия. Это положение описывается числом Френеля. Оно вычисляется так:

Где a — геометрические размеры препятствия (например, щели или круглого отверстия), λ — длина волны, D — дистанция между экраном и препятствием. Если для конкретного эксперимента F 1, тогда имеет место приближение ближнего поля или дифракция Френеля.

Разница между дифракциями Фраунгофера и Френеля заключается в различных условиях для явления интерференции на маленьком и большом расстояниях от препятствия.

Вывод формулы главных максимумов дифракционной решетки, который будет приведен далее в статье, предполагает рассмотрение дифракции Фраунгофера.

Дифракционная решетка и ее виды

Эта решетка представляет собой пластинку из стекла или прозрачного пластика размером в несколько сантиметров, на которую нанесены непрозрачные штрихи одинаковой толщины. Штрихи расположены на постоянном расстоянии d друг от друга. Это расстояние носит название периода решетки. Две других важных характеристики прибора — это постоянная решетки a и число прозрачных щелей N. Величина a определяет количество щелей на 1 мм длины, поэтому она обратно пропорциональна периоду d.

Существует два типа дифракционных решеток:

• Прозрачная, которая описана выше. Дифракционная картина от такой решетки возникает в результате прохождения через нее волнового фронта.
• Отражающая. Она изготавливается с помощью нанесения маленьких бороздок на гладкую поверхность. Дифракция и интерференция от такой пластинки возникают за счет отражения света от вершин каждой бороздки.

Какой бы ни был тип решетки, идея ее воздействия на волновой фронт заключается в создании периодического возмущения в нем. Это приводит к образованию большого количества когерентных источников, результатом интерференции которых является дифракционная картина на экране.

Основная формула дифракционной решетки

Вывод этой формулы предполагает рассмотрение зависимости интенсивности излучения от угла его падения на экран. В приближении дальнего поля получается следующая формула для интенсивности I(θ):

В формуле ширина щели дифракционной решетки обозначается символом a. Поэтому множитель в круглых скобках отвечает за дифракцию на одной щели. Величина d — это период дифракционной решетки. Формула показывает, что множитель в квадратных скобках, где появляется этот период, описывает интерференцию от совокупности щелей решетки.

Пользуясь приведенной формулой, можно рассчитать значение интенсивности для любого угла падения света.

Если находить значение максимумов интенсивности I(θ), то можно прийти к выводу, что они появляются при условии, что α = m*pi, где m является любым целым числом. Для условия максимумов получаем:

Полученное выражение называется формулой максимумов дифракционной решетки. Числа m — это порядок дифракции.

Другие способы записи основной формулы для решетки

Заметим, что в приведенной в предыдущем пункте формуле присутствует член sin(θ). Здесь угол θ отражает направление падения фронта световой волны относительно плоскости решетки. Когда фронт падает параллельно этой плоскости, то θ = 0o. Тогда получаем выражение для максимумов:

Поскольку постоянная решетки a (не путать с шириной щели) обратно пропорциональна величине d, то через постоянную дифракционной решетки формула выше перепишется в виде:

Чтобы не возникало ошибок при подстановке конкретных чисел λ, a и d в эти формулы, следует всегда использовать соответствующие единицы СИ.

Понятие об угловой дисперсии решетки

Будем обозначать эту величину буквой D. Согласно математическому определению, она записывается следующим равенством:

Физический смысл угловой дисперсии D заключается в том, что она показывает, на какой угол dθ_m сместится максимум для порядка дифракции m, если изменить длину падающей волны на dλ.

Если применить это выражение для уравнения решетки, тогда получится формула:

Дисперсия угловая дифракционной решетки определяется по формуле выше. Видно, что величина D зависит от порядка m и от периода d.

Чем больше дисперсия D, тем выше разрешающая способность данной решетки.

Разрешающая способность решетки

Под разрешающей способностью понимают физическую величину, которая показывает, на какую минимальную величину могут отличаться две длины волны, чтобы их максимумы на дифракционной картине появлялись раздельно.

Разрешающая способность определяется критерием Рэлея. Он гласит: два максимума можно разделить на дифракционной картине, если расстояние между ними оказывается больше полуширины каждого из них. Угловая полуширина максимума для решетки определяется по формуле:

Разрешающая способность решетки в соответствии с критерием Рэлея равна:

Подставляя значения D и Δθ_1/2, получаем:

Это и есть формула разрешающей способности дифракционной решетки. Чем больше число штрихов N на пластинке и чем выше порядок дифракции, тем больше разрешающая способность для данной длины волны λ.

Дифракционная решетка в спектроскопии

Выпишем еще раз основное уравнение максимумов для решетки:

Здесь видно, что чем больше длина волны падает на пластинку со штрихами, тем при больших значениях углов будут появляться максимумы на экране. Иными словами, если через пластинку пропустить немонохроматический свет (например, белый), то на экране можно видеть появление цветных максимумов. Начиная от центрального белого максимума (дифракция нулевого порядка), дальше будут появляться максимумы для более коротких волн (фиолетовый, синий), а затем для более длинных (оранжевый, красный).

Другой важный вывод из этой формулы заключается в зависимости угла θ_m от порядка дифракции. Чем больше m, тем больше значение θ_m. Это означает, что цветные линии будут сильнее разделены между собой на максимумах для высокого порядка дифракции. Этот факт уже был освящен, когда рассматривалась разрешающая способность решетки (см. предыдущий пункт).

Описанные способности дифракционной решетки позволяют использовать ее для анализа спектров излучения различных светящихся объектов, включая далекие звезды и галактики.

Пример решения задачи

Покажем, как пользоваться формулой дифракционной решетки. Длина волны света, которая падает решетку, равна 550 нм. Необходимо определить угол, при котором появляется дифракция первого порядка, если период d равен 4 мкм.

Угол θ₁ легко рассчитать по формуле:

Переводим все данные в единицы СИ и подставляем в это равенство:

Если экран будет находиться на расстоянии 1 метр от решетки, то от середины центрального максимума линия первого порядка дифракции для волны 550 нм появится на расстоянии 13,8 см, что соответствует углу 7,9o.

Спектральные приборы. Дифракционная решетка

В состав видимого спектра света включены монохроматические волны с различными длинами. В излучении нагретых объектов (к примеру, нити лампы накаливания) длины волн беспрерывно заполняют весь диапазон видимого света. Данное излучение называют белым светом.

Свет, излучаемый, например, газоразрядными лампами или одним из множества других подобных им приборами, включает в свой состав отдельные монохроматические составляющие с некоторыми выделенными значениями длин волн.

Комплекс монохроматических компонент в излучении называется спектром.

Белый свет имеет непрерывный спектр, излучение источников, в которых он испускается атомами вещества, и дискретный спектр.

Спектральные приборы – это устройства, с помощью которых изучаются спектры излучения источников.

Для разложения излучения в спектр в простейшем спектральном приборе используется призма избраженная на картинке 3 . 10 . 1 .

Действие призмы базируется на таком явлении, как дисперсия, то есть на привязанности показателя преломления n вещества к длине волны света λ .

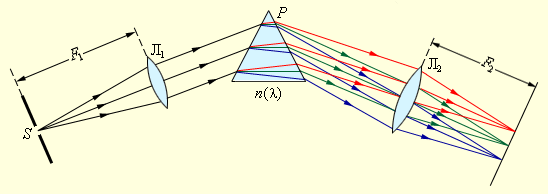
Рисунок 3 . 10 . 1 . Разложение излучения в спектр с помощью призмы.

Щель S , на которую падает рассматриваемое излучение, располагается в фокальной плоскости линзы Л 1 . Этот элемент прибора называется коллиматором.

Выходя из линзы, параллельный пучок света падает на призму P . По причине дисперсии, свет различных длин волн излучается из призмы под разнящимися углами. В фокальной плоскости линзы Л 2 устанавливают экран или фотопластинку, для фокусировки места излучения. Таким образом, в разных частях экрана появляется проекция входной щели S в свете различных длин волн.

У любого прозрачного твердого вещества (стекло, кварц), из которого изготавливаются призмы, показатель преломления n в диапазоне видимого света уменьшается с возрастанием длины волны λ , из-за чего призма наиболее сильно отклоняет, от их изначального направления, синие и фиолетовые лучи, а красные – наименее. Убывающая без ускорения зависимость n ( λ ) носит название нормальной дисперсии.

Первый опыт по разложению белого света в спектр осуществил известный физик И. Ньютон в 1672 году.

Дифракционные решетки

В спектральных приборах, относящихся к высокому классу точности, место призм занимают дифракционные решетки. Они представляют из себя периодические конструкции, которые гравируют, посредством использования особой делительной машины, на поверхности стеклянной или металлической пластинки (рис. 3 . 10 . 2 ).

У качественных решеток штрихи, параллельные друг другу, имеют длину около 10 с м , где на каждый миллиметр решетки приходится до 2000 штрихов. Причем, общая длина решетки может достигать 10 – 15 с м . Создание подобных решеток требует применения технологий самого высокого класса. Практически используются и более грубые версии решетки с 50 – 100 штрихами на миллиметр, которые нанесены на поверхность прозрачной пленки. В роли дифракционной решетки может применяться небольшая часть компакт-диска или даже осколок граммофонной пластинки.

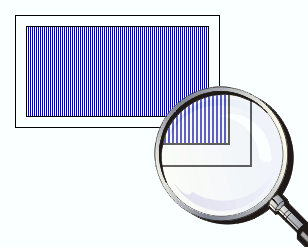
Рисунок 3 . 10 . 2 . Дифракционная решетка.

Самый простой тип дифракционной решетки производится из прозрачных участков, то есть щелей, которые разделены непрозрачными промежутками. С помощью коллиматора, на решетку направляется параллельный пучок исследуемого света. Наблюдение проводится в фокальной плоскости линзы, установленной за плоскостью решетки (рис. 3 . 10 . 3 ).

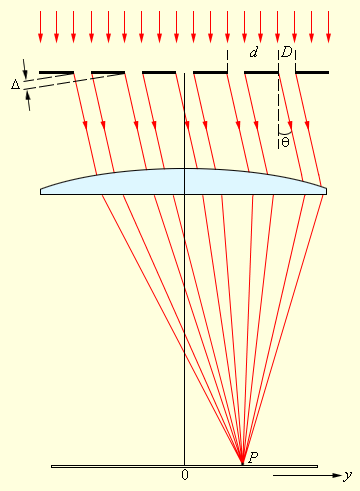
Рисунок 3 . 10 . 3 . Дифракция света на решетке.

В каждой точке P на экране в фокальной плоскости линзы сходятся лучи, который до линзы являлись параллельными между собой и расходились под некоторым углом θ к направлению падающей волны.

Интерференция волн

Колебание в точке P представляют собой следствие интерференции вторичных волн, которые сходятся в эту точку от разных щелей.

Для того, чтобы в точке P прослеживался интерференционный максимум, разность хода Δ между волнами, который испускают соседние щели, должна быть эквивалентной целому числу длин волн:

∆ = d sin θ m = m λ ( m = 0 , ± 1 , ± 2 , . . . ) .

Где d – это период дифракционной решетки, а m – целое число, носящее название порядка дифракционного максимума. В точках экрана, для которых это условие выполнено, расположены главные максимумы дифракционной картины.

В фокальной плоскости линзы, расстояние y m между максимумами нулевого порядка ( m = 0 ) и m -го порядка при сравнительно малых углах дифракции равняется:

где F – фокусное расстояние.

Также следует обратить внимание на то, что в каждой точке фокальной плоскости линзы, имеет место интерференция N волн, которые приходят в эту точку от N щелей решетки. Данный феномен является так называемой многоволновой или же «многолучевой» интерференцией.

Распространение световой энергии в плоскости наблюдения значительно отличается от того, которое выходит в обыкновенных «двухлучевых» интерференционных схемах. В главные максимумы все волны приходят в фазе, из-за чего амплитуда колебаний увеличивается в N раз, а интенсивность в N 2 раз, относительно колебания, которое провоцирует волна только от одной конкретной щели.

В условиях смещения из главных максимумов, стремительно теряется интенсивность колебаний. Для того, чтобы N волн погасили друг друга, значение разности фаз должно измениться на 2 π N , а не на π , как в случае интерференции двух волн.

На рис. 3 . 10 . 4 можно увидеть векторную диаграмму колебаний, возбуждаемых волнами от всех N щелей, если сдвиг фаз волн от соседних щелей равен 2 π N , а соответствующая разность хода равна отношению λ N .

Векторы, иллюстрирующие N колебаний, в данной ситуации формируют замкнутый многоугольник. Следовательно, при переходе из главного максимума в соседний минимум, разность хода Δ = d sin θ смениться на λ N . Исходя из данного условия, справедливым будет оценить угловую полуширину δ θ главных максимумов:

δ ∆ = δ ( d sin θ ) = d cos θ δ θ ≈ d · δ θ = λ N .

Здесь, дифракционные углы считаются достаточно малыми. Таким образом,

Где N d – это полный размер решетки. Данное выражение находится в полной симметрии с теорией дифракции в параллельных лучах. Согласно этой теории, дифракционная расходимость параллельного пучка лучей эквивалентна отношению длины волны λ к поперечному размеру препятствия.

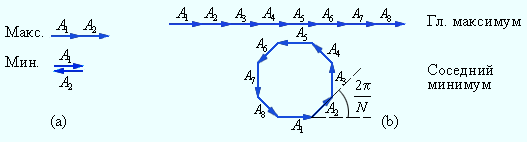
Рисунок 3 . 10 . 4 . Сложение колебаний в максимуме и минимуме интерференционной картины: a – интерференция двух волн, b – интерференция N волн ( N = 8 ) .

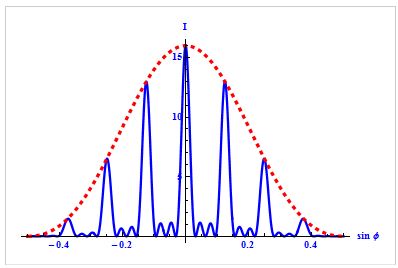
Из описанного выше, можно сделать однозначный вывод: при дифракции света на решетке главные максимумы крайне узки. Рис. 3 . 10 . 5 иллюстрирует изменение остроты главных максимумов при возрастании количества щелей решетки.

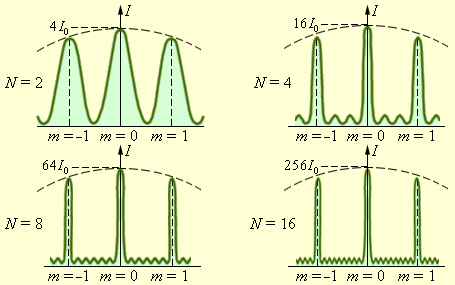
Рисунок 3 . 10 . 5 . Распределение интенсивности при дифракции монохроматического света на решетках с различным числом щелей. I 0 – интенсивность колебаний при дифракции света на одной щели.

Исходя из формулы дифракционной решетки, мы можем заявить, что положение главных максимумов, кроме нулевого, зависит от длины волны λ . По этой причине решетка может разбивать излучение в спектр. Следовательно, она является спектральным прибором. В случае, если на решетку попадает не монохроматическое излучение, то в каждом порядке дифракции, а именно при каждом значении m , проявляется спектр исследуемого излучения.

Также стоит обратить внимание на то, что фиолетовая часть спектра расположена ближе к максимуму нулевого порядка. На рис. 3 . 10 . 6 для белого света проиллюстрированы спектры различных порядков. Максимум нулевого порядка остается неокрашенным.

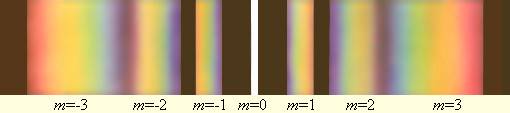
Рисунок 3 . 10 . 6 . Разложение белого света в спектр с помощью дифракционной решетки.

Используя дифракционную решетку, мы получаем возможность производить крайне точные измерения длины волны. При условии, что период d решетки известен, нахождение искомой величины (длины) приводится к измерению угла θ m , соответствующего направлению на выбранной линии в спектре m-го порядка. На практике, чаще всего применяются спектры 1 -го или 2 -го порядков.

Решетка в любом спектральном порядке (кроме m = 0 ) имеет возможность отсоединить одну волну от другой в случае, если в спектре изучаемого излучения есть две спектральные линии, обладающие длинами волн λ 1 и λ 2 .

Разрешающая способность дифракционной решетки – это одна из основных ее характеристик. Ей характеризуется возможность разделения при использовании решетки двух близких спектральных линий с длинами волн λ и λ + Δ λ .

Спектральная разрешающая способность R является отношением длины волны λ к минимальному реальному значению Δ λ , то есть: R = λ ∆ λ

Волновая природа света

Волновая природа света определяет разрешающую способность спектральных приборов, в частности, дифракционной решетки, так же от нее зависит предельное разрешение различных оптических инструментов, которые создают изображение объектов, таких как телескоп, микроскоп и др.

Считается, что если главный максимум для длины волны λ + Δ λ отступает от главного максимума для длины волны λ не менее, чем на полуширину главного максимума, т. е. на δ θ = λ N d , то две ближайшие линии в спектре m-го порядка различимы. Вывод выше является критерием Релея, примененным к спектральному прибору.

Из формулы решетки следует:

d d · cos θ · ∆ θ = m ∆ λ или ∆ θ = m δ cos θ ∆ λ ≈ m d ∆ λ

Где Δ θ является угловым расстоянием между двумя главными максимумами в спектре m -го порядка для двух близких спектральных линий с разницей длин волн Δ λ . Для упрощения, углы дифракции предполагаются незначительно малыми ( cos θ ≈ 1 ) . Уравнивая Δ θ и δ θ , получаем оценку разрешающей силы решетки:

λ N d = m d ∆ λ или R = λ ∆ λ = m N .

Из описанного выше следует, что предельное разрешение дифракционной решетки может зависеть только от порядка спектра m и от количества периодов решетки N .

Пускай период решетки d = 10 – 3 м м , а ее длина L = 10 с м .

Решение

В таком случае, N = 10 5 .

Исходя из данных показателей, можно с уверенностью сказать, что это хорошая решетка. В спектре 2 -го порядка разрешающая способность решетки равна R = 2 · 10 5 . Это указывает на то, что минимально разрешенный диапазон длин волн в зеленой части спектра (т.е. при λ = 550 н м ) равен Δ λ = λ R ≈ 2 , 8 · 10 – 3 н м , а предельное разрешение решетки с d = 10 – 2 м и L = 2 с м было бы равным Δ λ = 1 , 4 · 10 – 1 н м .

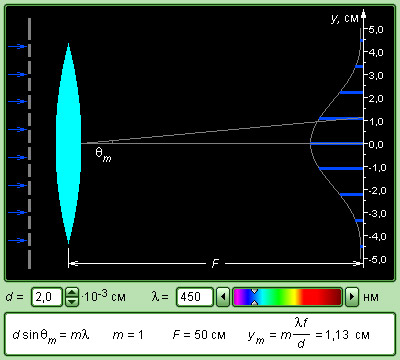
Рисунок 3 . 10 . 7 . Модель дифракционной решетки.

Физика. 11 класс

Конспект урока

Физика, 11 класс

Урок 17. Дифракция света

Перечень вопросов, рассматриваемых на уроке:

1) условия возникновения явления дифракции света.

2) знания о дифракционной решетке.

3) понятие дифракции, где наблюдается данное явление в природе.

4) представление о дифракции, как о явлении, подтверждающее волновую теорию света;

5) знакомство с спектральным прибором (дифракционная решетка).

Глоссарий по теме

Интерференция и дифракция – явления, подтверждающие волновую природу света.

Дифракция света – огибание световой волной непрозрачных тел с проникновением в область геометрической тени и образованием там интерференционной картины.

Принцип Гюйгенса – каждая точка поверхности, достигнутая световой волной, является вторичным источником световых волн. Огибающая вторичных волн, становится волновой поверхностью в следующий момент времени.

Френеля Принцип Гюйгенса – каждый элемент волнового фронта можно рассматривать как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн.

Дифракционная решётка – представляет собой совокупность большого числа узких щелей, разделенных непрозрачными промежутками.

Основная и дополнительная литература по теме урока:

Мякишев Г.Я, Буховцев Б Б. Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 213 – 220.

Рымкевич А.П. Сборник задач по физике. 10-11 класс.-Москва «Просвещение»1992. С.149 – 151

Основное содержание урока

Дифракция – огибание волнами краёв препятствий – присуща любому волновому движению

Но наблюдать дифракцию света нелегко, так как волны отклоняются от прямолинейного распространения на заметные углы только на препятствиях, размеры которых сравнимы с длиной волны, а длина световой волны, как мы с вами знаем, очень мала.

В 1802 г. Томас Юнг, поставил опыт по дифракции.

В непрозрачной ширме он сделал два маленьких отверстия на небольшом расстоянии друг от друга. Эти отверстия освещались узким световым пучком, прошедшим через первое отверстие в другой ширме. Волна от первого отверстия возбуждала когерентные колебания в двух других отверстиях. Вследствие дифракции из двух отверстий выходили два световых конуса, которые частично перекрывались. В результате интерференции этих двух световых волн на экране появились чередующиеся светлые и тёмные полосы. При закрывании Юнгом одной из отверстий, было обнаружено, что интерференционные полосы исчезали. Именно этот опыт помог Юнгу измерить длины волн, соответствующие световым лучам разного цвета. Следующий учёный Френель завершил в своих работах исследования дифракции. Он разработал количественную теорию дифракции, позволяющую в принципе рассчитать дифракционную картину, возникающую при огибании светом любых препятствий. Учёный впервые объяснил прямолинейное распространение света в однородной среде на основе волновой теории.

По идее Френеля каждая точка волнового фронта является источником вторичных волн, причём все вторичные источники когерентны.

На явлении дифракции основано устройство оптического прибора – дифракционной решётки

Дифракционная решётка представляет собой совокупность большого числа очень узких щелей, разделённых непрозрачными промежутками.

Если ширина прозрачных щелей равна а, и ширина непрозрачных промежутков равна b, то величина d = а + b называется периодам решётки.

Обычно период дифракционной решётки порядка 10 мкм.

Разбор тренировочных заданий

1.Дифракционная решетка освещается монохроматическим зеленым светом. При освещении решетки монохроматическим красным светом картина дифракционного спектр.

1) сузится; 2) расширится; 3) исчезнет;4) не изменится

Правильный ответ: 2) расширится

2. Сколько штрихов на каждый миллиметр содержит дифракционная решётка, если при наблюдении в монохроматическом свете 𝛌 = 0,6 мкм максимум пятого отклонён на угол φ = 18°.

Дифракционная решетка формулы, период, виды дифракции света

Дифракция – явление отклонения световых волн от прямолинейного распространения при прохождении света мимо края препятствия. При этом лучи могут попадать в область геометрической тени от препятствия.

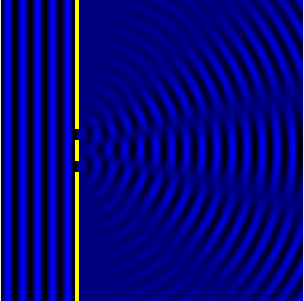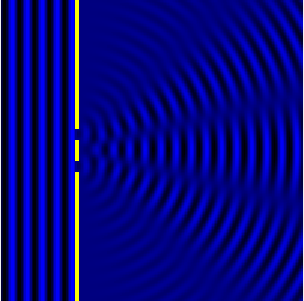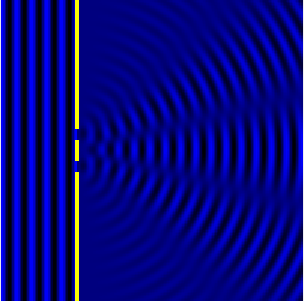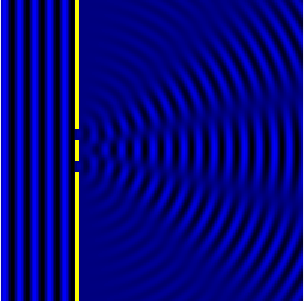
Между интерференцией и дифракцией нет существенного физического различия. Оба явления заключаются в перераспределении светового потока в результате наложения (суперпозиции) волн. По историческим причинам отклонение от закона независимости световых пучков, возникающее в результате суперпозиции когерентных волн, принято называть интерференцией волн . Отклонение от закона прямолинейного распространения света, в свою очередь, принято называть дифракцией волн .

Наблюдение дифракции осуществляется обычно по следующей схеме. На пути световой волны, распространяющейся от некоторого источника, помещается непрозрачная преграда, закрывающая часть волновой поверхности световой волны. За преградой располагается экран, на котором возникает дифракционная картина.

Различают два вида дифракции. Если источник света S и точка наблюдения P расположены от препятствия настолько далеко, что лучи, падающие на препятствие, и лучи, идущие в точку P, образуют практически параллельные пучки, говорят о дифракции в параллельных лучах или о дифракции Фраунгофера . В противном случае говорят о дифракции Френеля . Количественный критерий, позволяющий установить, какой вид дифракции имеет место, определяется величиной безразмерного параметра b 2 /lλ, где b – характерный размер препятствия, l – расстояние между препятствием и экраном, на котором наблюдается дифракционная картина, λ – длина волны.

Свойства дифракции:

1) Дифракция волн – характерная особенность распространения волн независимо от их природы.

2) Волны могут попадать в область геометрической тени (огибать препятствия, проникать через не­большие отверстия в экранах). На­пример, звук хорошо слышен за углом дома – звуковая волна его огибает. Дифракцией радиоволн вокруг поверхности Земли объясняется прием радиосигналов в диапазоне длинных и средних радиоволн за пределами прямой видимости излучающей антенны.

3) Дифракция волн зависит от соотношения между длиной волны и размером объекта, вызывающего дифракцию. В пределе при λ→0 законы волновой оптики переходят в законы геометрической оптики. Дифракция обнаруживается в тех случаях, когда размеры огибаемых препятствий соизмеримы с длиной волны.

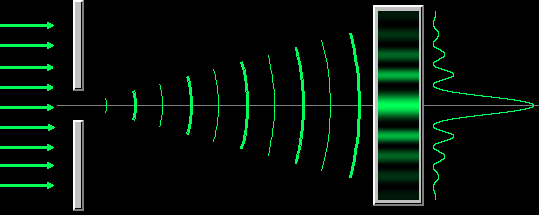
Объяснить явление дифракции можно исходя из принципа Гюйгенса-Френеля .Этот принцип представляет собой правило, объясняющее, как, исходя из положения волнового фронта в данный момент, найти новое положение волнового фронта в последующий момент времени.

Гюйгенс предложил рассматривать каждую точку среды, которой достигла волна, как источник вторичных сферических волн, распространяющихся по всем направлениям со скоростью, присущей данной среде . Поверхность, огибающая вторичные волны, представляет собой фронт волны в данный момент времени.

Френель дополнил изложенный принцип следующим положением: вторичные сферические волны являются когерентными и колебания в любой точке пространства, которой вторичные волны достигнут в момент времени t, представляют собой результат интерференции этих вторичных волн .

Принцип Гюйгенса – Френеля формулируется следующим образом:

Каждый элемент волнового фронта можно рассматривать как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн.

Дифракция Фраунгофера от одной щели

Дифракция Фраунгофера наблюдается, когда источник света сильно удален от места наблюдения, в результате фронт волны можно считать плоским.

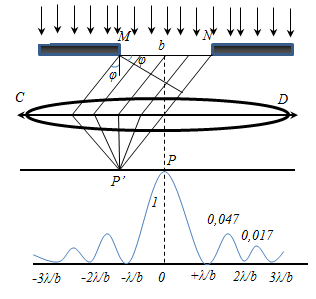
Разность хода двух волн от краев щели равна Δ = b sin φ .

Разобьем MN на отрезки длиной λ/2. Параллельно произвольному направлению луча через точки разбиения (1, 2, 3) проведем линии, которые разделят открытую часть волновой поверхности MN на участки равной ширины – зоны Френеля, параллельные краям щели. По построению ∆ – разность хода лучей от краев зон Френеля равна λ/2. Это означает, что волны, идущие от двух соседних зон при наложении погасят друг друга. Т.о., если на открытой части волновой поверхности для данного направления наблюдения уложится целое четное число зон Френеля, то для данного направления будет наблюдаться min интенсивности, т.к. зоны попарно друг друга погасят.

Четное число зон Френеля – минимум дифракции

Если число зон Френеля целое и нечетное, то в этом направлении будет наблюдаться max:

Дифракционная решетка

Совокупность большого числа щелей и промежутков между ними называется дифракционной решеткой.

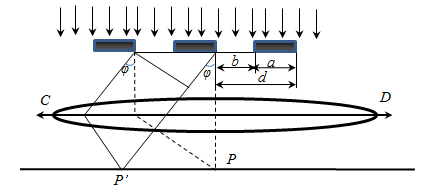
а – ширина промежутка между щелями;

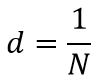
N – число щелей, приходящихся на единицу длины

Дифракционная картина на решетке определяется как интерференция волн, приходящих от всех щелей, т. е. дифракция на решетке – многолучевая интерференция. Поскольку щели разделены одинаковым расстоянием, разности хода лучей, поступающих из двух соседних щелей, будут для направления φ идентичны по всей решетке.

В областях, в которых существует минимум при одной щели, минимумы будут и в случае N щелей, т. е. условие первичного минимума дифракционной решетки аналогично условию минимума для одной щели:

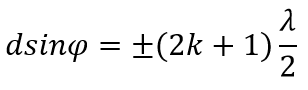– условие главных минимумов.

Условие главных максимумов :

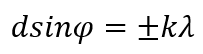
Эти максимумы расположены симметрично относительно центра (k = 0) и главного максимума.

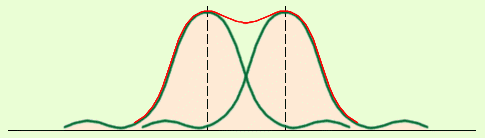
Между основными пиками есть дополнительные очень слабые пики, интенсивность которых значительно меньше, чем у основных пиков (1/22 интенсивности ближайшего главного максимума). Количество дополнительных максимумов равно N – 2, где N – количество штрихов решетки.

Между главными максимумами будут расположены (N-1) дополнительных минимумов.

Разрешающая способность дифракционной решетки

Размер дифракционных изображений очень мал. Например, радиус центрального светлого пятна в фокальной плоскости линзы диаметром D = 5 см с фокусным расстоянием F = 50 см в монохроматическом свете с длиной волны λ = 500 нм приблизительно равен 0,006 мм. Но в высокоточных астро­но­ми­ческих приборах реализуется дифракци­он­ный предел качества изо­бра­же­ний. Вслед­ствие дифракционного размытия изобра­жения двух близких точек объекта могут оказаться неотличимыми от изо­бра­же­ния одной точки.

Спектральной разрешающей способностью R решетки, характеризующей возможность разделения с ее помощью двух близких спектральных линий с длинами волн λ и λ + Δλ, называется отношение длины волны λ к минимально возможному значению Δλ

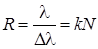
Пусть решетка имеет период d = 10 –3 мм, ее длина L = 10 см. Тогда, N = 10 5 (это хорошая решетка). В спектре 2-го порядка разрешающая способность решетки оказывается равной R = 2·10 5 . Это означает, что минимально разрешимый интервал длин волн в зеленой области спектра (λ = 550 нм) равен Δλ = λ / R ≈ 2,8·10 –3 нм.

Действие оптических приборов описывается законами геометрической оптики. Согласно этим законам можно различать с помощью микроскопа сколь угодно малые детали объекта; с помощью телескопа можно установить существование двух звезд при любых малых угловых расстояниях между ними. Однако в действительности это не так, и лишь волновая теория света позволяет разобраться в причинах предела разрешающей способности оптических приборов.

Метод зон Френеля

Границей первой (центральной) зоны служат точки поверхности S, находящиеся на расстоянии l + λ/2 от точки M. Точки сферы S, находящиеся на расстояниях l + 2λ/2, l + 3λ/2 , и т.д. от точки M , образуют 2, 3 и т.д. зоны Френеля.

Колебания, возбуждаемые в точке M между двумя соседними зонами, противоположны по фазе, так как разность хода от этих зон до точки M Δ = λ/2.

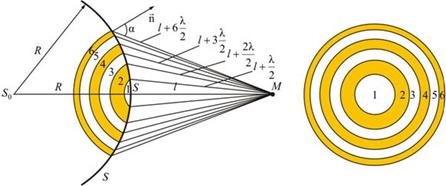
Поэтому при сложении этих колебаний, они должны взаимно ослаблять друг друга: A = A₁ + A₂ + A₃ +. + A_i.

где A – амплитуда результирующего колебания, A_i – амплитуда колебаний, возбуждаемая i-й зоной Френеля.

Величина A_i зависит от площади S_i зоны и угла α_i между нормалью к поверхности и прямой, направленной в точку M.

Площадь одной зоны

Отсюда видно, что площадь зоны Френеля не зависит от номера зоны i. Это значит, что при не слишком больших i площади соседних зон одинаковы.

В то же время с увеличением номера зоны возрастает угол α_i и, следовательно, уменьшается интенсивность излучения зоны в направлении точки M, т.е. уменьшается амплитуда A_i. Она уменьшается также из-за увеличения расстояния до точки M .

Отсюда следует, что углы между нормалью к зоне и направлением на точку M у соседних зон примерно равны, т.е. что амплитуды волн, приходящих в точку M от соседних зон, примерно равны.

Приближенно можно считать, что амплитуда колебания A m от некоторой m -й зоны равна среднему арифметическому от амплитуд примыкающих к ней зон, т.е.

.

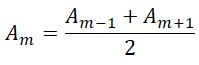
Тогда выражение для амплитуды можно записать в виде

Так как площади соседних зон одинаковы, то выражения в скобках равны нулю, значит результирующая амплитуда А = A₁ /2.

Интенсивность излучения J

Таким образом, результирующая амплитуда, создаваемая в некоторой точке M всей сферической поверхностью, равна половине амплитуды, создаваемой одной лишь центральной зоной, а интенсивность J = J₁/4 .

Так как радиус центральной зоны мал ( r₁ = 0,16 мм), следовательно, можно считать, что свет от точки P до точки M распространяется прямолинейно.

Если на пути волны поставить непрозрачный экран с отверстием, оставляющим открытой только центральную зону Френеля, то амплитуда в точке M будет равна A₁. Соответственно, интенсивность в точке M будет в 4 раза больше, чем при отсутствии экрана (т.к. J = 4J₁ ). Интенсивность света увеличивается, если закрыть все четные зоны.

Таким образом, принцип Гюйгенса–Френеля позволяет объяснить прямолинейное распространение света в однородной среде.

Дифракция на простых объектах

Дифракция на щели

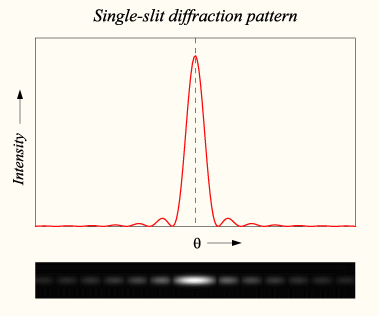
Дифракция от круглого отверстия
Поставим на пути сферической световой волны непрозрачный экран с круглым отверстием радиуса . Экран расположен так, что перпендикуляр, опущенный из S на непрозрачный экран, попадает точно в центр отверстия.

Разобьем открытую часть волновой поверхности на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, открываемых отверстием. К огда отверстие открывает нечетное число зон Френеля, то амплитуда (интенсивность) в точке М будет больше, чем при свободном распространении волны; если четное, то амплитуда (интенсивность) будет равна нулю.

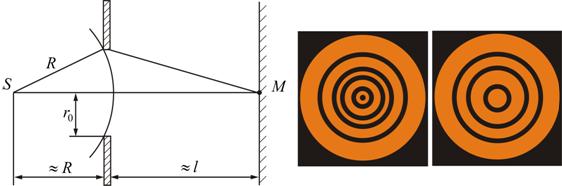
Дифракция на круглом отверстии при открытом чётном (слева) и не чётном (справа) числе зон.

Естественно, что если r>>λ, то никакой дифракционной картины не будет.

Дифракция от диска
Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск.

В центре тени светлое пятно

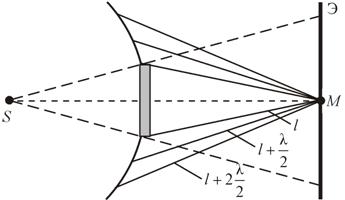
Амплитуда световых колебаний в точке M равна половине амплитуды, обусловленной первой открытой зоной. Если размер диска невелик (охватывает небольшое число зон), то действие первой зоны немногим отличается от действия центральной зоны волнового фронта. Таким образом, освещенность в точке M будет такой же, как и в отсутствие экрана. Вследствие симметрии центральная светлая точка будет окружена кольцами света и тени (вне границ геометрической тени).

Парадоксальное, на первый взгляд, заключение, в силу которого в самом центре геометрической тени может находиться светлая точка, было выдвинуто Пуассоном в 1818 г. и впоследствии было названо его именем. «Пятно Пуассона» подтверждает правильность теории Френеля.

Дифракция света

В рамках геометрической оптики, распространение луча в оптически однородной среде — прямолинейное, однако в природе существует ряд явлений, где можно наблюдать отклонение от этого условия.

Дифракция – явление огибания световыми волнами встреченных препятствий. В школьной физике изучаются две дифракционные системы (системы, при прохождении луча в которых наблюдается дифракция):

• дифракция на щели (прямоугольном отверстии)
• дифракция на решётке (набор равноотстоящих друг от друга щелей)

Дифракция на щели — дифракция на прямоугольном отверстии (рис. 1).

Рис. 1. Дифракция на щели

Пусть дана плоскость со щелью, шириной , на которую под прямым углом падает пучок света А. Большинство света проходит на экран, однако часть лучей дифрагирует на краях щели (т.е. отклоняется от своего первоначального направления). Далее эти лучи интерферируют друг с другом с образованием дифракционной картины на экране (чередование ярких и тёмных областей). Рассмотрение законов интерференции достаточно сложно, поэтому ограничимся основными выводами.

Полученная дифракционная картина на экране состоит из чередующихся областей с дифракционными максимумами (максимально светлыми областями) и дифракционными минимумами (максимально тёмными областями). Эта картина симметрична относительно центрального светового пучка. Положение максимумов и минимумов описывается углом относительно вертикали, под которым они видны, и зависит от размера щели и длины волны падающего излучения. Положение этих областей можно найти используя ряд соотношений:

• для дифракционных максимумов

• где
  • — ширина щели,
  • — угол между вертикалью и направлением на максимум,
  • — порядок максимума (счётчик),
  • — длина волны света.

Нулевым максимумом дифракции называется центральная точка на экране под щелью (рис. 1).

• для дифракционных минимумов

• где
  • — ширина щели,
  • — угол между вертикалью и направлением на минимум,
  • — порядок минимума (счётчик),
  • — длина волны света.

Вывод: по условиям задачи необходимо выяснить: максимум или минимум дифракции необходимо найти и использовать соответствующее соотношение (1) или (2).

Дифракция на дифракционной решётке.

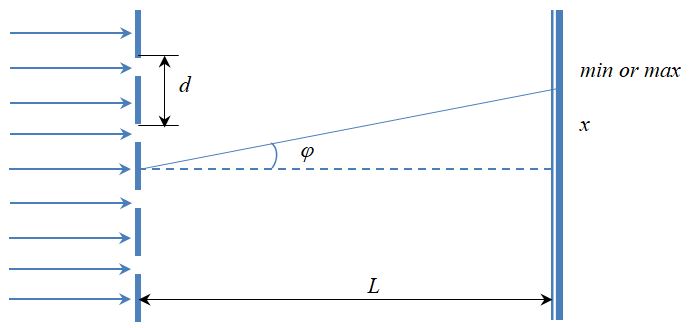
Дифракционной решёткой называется система, состоящая из чередующихся щелей, равноотстоящих друг от друга (рис. 2).

Рис. 2. Дифракционная решётка (лучи)

Так же, как и для щели, на экране после дифракционной решётки будет наблюдаться дифракционная картина: чередование светлых и тёмных областей. Вся картина есть результат интерференции световых лучей друг с другом, однако на картину от одной щели будет воздействовать лучи от других щелей. Тогда дифракционная картина должна зависеть от количества щелей, их размеров и близкорасположенности.

Введём новое понятие — постоянная дифракционной решётки:

• где
  • — постоянная дифракционной решётки,
  • — расстояние между щелями,
  • — ширина щели.

Тогда положения максимумов и минимумов дифракции:

• для главных дифракционных максимумов (рис. 3)

• где
  • — постоянная дифракционной решётки,
  • — угол между вертикалью и направлением на максимум.
  • — порядок максимума (счётчик),

Рис. 3. Дифракционная решётка (максимумы)

• для дифракционных минимумов

• где
  • — ширина щели,
  • — угол между вертикалью и направлением на минимум,
  • — порядок минимума (счётчик),
  • — длина волны света.

Отдельным вопросом задач на дифракцию является вопрос о наибольшем количестве максимумов, которые можно наблюдать в текущей системе. Наибольший угол, под которым можно наблюдать максимум — , тогда, исходя из (4):

Главное помнить, что число максимумов — число, т.е. от полученного ответа необходимо брать только целую часть.

Вывод: по условиям задачи необходимо выяснить: максимум или минимум дифракции необходимо найти и использовать соответствующее соотношение (4) или (5).

Общий вывод: задачи на дифракцию должны содержать в себе словосочетания, связанные с «дифракцией». Далее разбираемся с объектом: щель или дифракционная решётка и используем соответствующие соотношения для минимума или максимума.

Дифракция света

теория по физике 🧲 оптика

Дифракция — явление, присущее всем волновым процессам подобно интерференции. Чтобы лучше понять, в чем заключается явление дифракции света, сначала рассмотрим дифракцию механических волн.

Дифракция механических волн

Иногда на пути волны встречаются препятствия разных размеров. Если препятствия небольшие, волны легко их огибают и смыкаются за ними. Поэтому морские волны свободно огибают выглядывающие из воды камни и распространяются за ними так, как если бы их не было совсем. Если размер препятствия больше длины волны, за ним образуется «тень» — область, в которую волны проникнуть не могут.

На рисунке ниже видно, что за мелкими камнями волны распространяются так же, как если бы их не было. Но за большой глыбой поверхность воды спокойная — волны в эту область не проникают.

Внимание! Малыми препятствиями будем считать те, размеры которых намного меньше длины распространяющейся волны или сравнимы с ней.

Способность волн огибать препятствия является следствием отклонения распространения волн от их прямолинейного распространения. Такой способностью обладают не только волны на поверхности воды, но и звуковые волны. Вы услышите, как сигналит автомобиль за домом, который стоит между ним и вами препятствием именно благодаря дифракции. Звуковая волна обогнет дом и продолжит распространяться за ним. По этой же причине в лесу так далеко распространяется клик «Ау!» — деревья для звуковой волны не являются серьезным препятствием, и она их легко огибает.

Дифракция — явление отклонения от прямолинейного распространения волн.

Дифракция волн проявляется особенно отчетливо в случаях, когда размеры препятствий меньше длины волны или сравнимы с ней. Это явление встречается в природе, но его также можно вызвать искусственно. К примеру, дифракцию волн на поверхности воды можно наблюдать, налив воду в ванночку и поставив на пути возбуждаемых волн искусственное препятствие.

Если на пути распространения волн поставить экран с узкой щелью, размеры которой меньше длины волны, то увидим, что за ней начинает распространяться круговая волна. Такая же волна получилась, если бы в щели экрана находилось колеблющееся тело — источник волн.

Если же на пути распространения волны поставить экран с широкой щелью, за ним будет распространяться волна почти такой же формы. Волновая поверхность в этом случае искривляется только по краям щели.

Понять, почему появляется явление дифракции волн, помогает принцип Гюйгенса. Согласно ему, каждая точка волновой поверхности является источником вторичных волн. Вторичные волны, испускаемые участками среды, проникают за края препятствия, расположенного на пути распространения волны.

Дифракция световых волн

Если свет — это волна, то ему тоже должно быть присуще явление дифракции. Однако наблюдать дифракцию света сложно. Ведь дифракцию можно наблюдать тогда, когда препятствие сравнимо с длиной волны или меньше ее. А длина световой волны очень мала. Поэтому чтобы наблюдать дифракцию света, нужны очень малые препятствия.

Дифракция света на узкой щели

Наблюдать отклонение от прямолинейного распространения света можно, если пропустить пучок световых волн через узкую щель. При этом светлое пятно на экране будет больше, чем сама щель. Это возможно только в случае, если свет отклоняется от своего прямолинейного распространения.

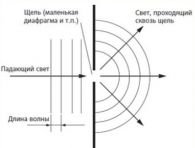
Опыт Юнга

В 1802 г. Т. Юнг, который открыл интерференцию света, поставил классический опыт по наблюдению дифракции. В непрозрачной ширме он проколол булавкой два небольших отверстия В и С на малом расстоянии друг от друга. Эти отверстия он осветил узким световым пучком, прошедшим через малое отверстие А в другой ширме. Именно эта деталь, до которой очень трудно было додуматься в то время, определила успех эксперимента. Интерферируют ведь только когерентные волны. Возникшая в соответствии с принципом Гюйгенса сферическая волна от отверстия А вызвала в отверстиях В и С образование когерентных источников световых волн. Вследствие дифракции от отверстий В и С выходили два световых конуса, которые частично перекрывались. В результате интерференции этих двух световых волн на экране появлялись картина, состоящая из чередующихся светлых и темных полос.

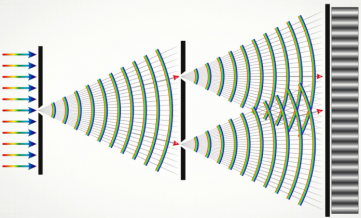
Закрыв одно из отверстий, Юнг обнаружил, что интерференционные полосы исчезали. Именно с помощью этого опыта впервые ученый измерил длины волн, соответствующие световым лучам разного цвета. И ему удалось сделать это с высокой точностью.

Принцип Гюйгенса — Френеля

Исследование дифракции завершил французский ученый О. Френель. Он занимался детальным исследованием различных случаев дифракции, что позволило ему разработать количественную теорию дифракции. Она помогла физику получить точные расчеты дифракционной картины, которая возникала при огибании светом различных препятствий. Френелю также удалось впервые объяснить, почему в однородной среде свет распространяется прямолинейно.

Успех Френеля объясняется тем, что он стал первым, кто решил объединить принцип Гюйгенса с идеей интерференции вторичных волн. В результате зародилась теория, которая получила название принципа Гюйгенса — Френеля:

Волновая поверхность в любой момент времени представляет собой не просто огибающую вторичных волн, а результат их интерференции.

Чтобы вычислить амплитуду световой волны в любой точке пространства, необходимо мысленно окружить источник света замкнутой поверхностью. Интерференция волн от вторичных источников, расположенных на этой поверхности, определяет амплитуду колебаний в рассматриваемой точке пространства. Такие расчеты дали объяснение тому, как свет от точечного источника S, являющегося источником сферических волн, достигает любой точки В пространства.

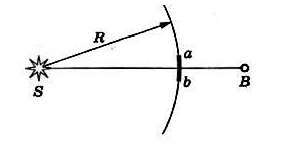
Если рассмотреть вторичные источники на сферической волновой поверхности радиусом R, то результат сложения вторичных волн от этих источников в точке В оказывается таким, как если бы только вторичные источники на малом сферическом сегменте ab посылали свет в точку В. Вторичные волны, распространяющие от источников, расположенных на остальной части поверхности, гасят друг друга в результате сложения. Поэтому все происходит так, как если бы свет распространялся вдоль прямой SB, т. е. прямолинейно. Эта теория Френеля доказала закон прямолинейного распространения света в однородной среде и позволила рассмотреть дифракцию с количественной точки зрения.

Внимание! Закон прямолинейного распространения света и другие законы геометрической оптики выполняются достаточно точно лишь в том случае, если размеры препятствий на пути распространения света много больше длины световой волны.

Дифракционные картины от различных препятствий

Расчеты Френеля получили экспериментальное подтверждение. Из-за малой длины световой волны угол ее отклонения от прямолинейного направления распространения небольшой. Поэтому наблюдать дифракцию можно только при использовании очень маленьких препятствий. Другой вариант наблюдения этого явления — расположение экрана вдали от препятствия.

Так, чтобы наблюдать дифракцию при расстоянии между экраном и препятствием в 1 м, размеры этого препятствия должны составлять сотые доли миллиметра. Если расстояние от препятствия до экрана увеличить до нескольких сотен метров, то размеры препятствия могут быть несколько сантиметров. Если расстояние между экраном и препятствием будет составлять несколько километров, дифракцию можно будет наблюдать при размерах препятствия в несколько метров.

Дифракционная картина — картина на экране, полученная в результате интерференции вторичных световых волн.

Подобную картину вы уже видели на картинке, иллюстрирующей опыт Юнга. Так, дифракционная картина от двух малых щелей — это чередующиеся темные и светлые полосы. Если использовать другие препятствия, картина будет меняться. На рисунке ниже схематично показаны дифракционные картины от различных препятствий: а — от тонкой проволочки; б — от круглого отверстия; в — от круглого экрана.

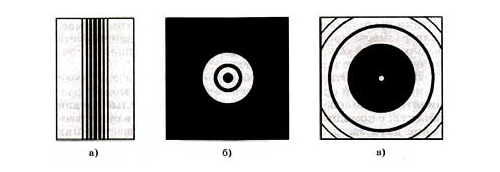
Вместо тени проволочка оставляет на экране светлые и темные полосы. В центре дифракционной картины, полученного от отверстия, появляется темное пятно, окруженное светлыми и темными кольцами. В центре тени, образованной круглым экраном, видно светлое пятнышко, а сама тень окружена темными кольцами. Если изменять диаметр отверстия, в центре дифракционной картины можно получить как светлое, так и темное пятно, окруженное либо темными, либо светлыми кольцами соответственно.

Дифракционная решетка

Дифракционная решетка — оптический прибор, принцип действия которого основан на явлении дифракции.

Дифракционная решетка представляет собой совокупность большого числа очень узких щелей, разделенных непрозрачными промежутками. Ее изготавливают путем нанесения на стекло штрихов. Их число может доходить до нескольких тысяч на 1 мм. Общее их число часто превышает 100 тысяч. Решетку также можно получить из металла, на котором чередуются участки, отражающие и рассеивающие свет.

• a — ширина прозрачных щелей (отражающих полос);
• b — ширина непрозрачных промежутков (рассеивающих полос);
• d — период дифракционной решетки.

Период дифракционной решетки равен сумме ширины прозрачных щелей и ширины непрозрачных промежутков:

Внимание! Обычно изготавливают дифракционные решетки с периодом в 10 мкм.

Пусть на дифракционную решетку с периодом d падает плоская монохроматическая волна, длина волны которой составляет λ.

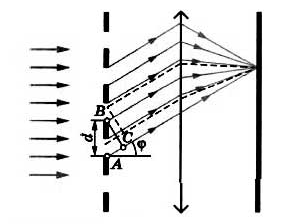
При этом вторичные источники, расположенные в щелях решетки, создают световые волны, распространяющиеся по всем направлениям. Найдем условие, при котором идущие от щелей волны усиливают друг друга (складываются). Для этого рассмотрим волны, распространяющиеся в направлении под углом φ к дифракционной решетке.

Разность хода между волнами от краев соседних щелей равна длине отрезка АС. Если на этом отрезке вмещается целое число длин волн, то волны от всех щелей при сложении будут усиливать друг друга. Из треугольника АВС найдем длину катета АС:

A C = A B sin . φ − d sin . φ

При этом максимумы будут наблюдаться под углом φ в соответствии с условием:

где величина k = 0, 1, 2, … определяет порядок спектра.

Нужно учитывать, что при выполнении условия друг друга усиливают как волны, распространяющиеся от нижних краев щелей, так и волны, распространяющиеся от всех других точек щелей. Каждой точке в первой щели соответствует точка во второй щели, находящаяся на расстоянии d от первой точки. Поэтому разность хода испущенных этими точками вторичных волн равна kλ, и эти волны взаимно усиливаются.

Рассмотрим следующий случай. За решеткой поместим собирающую линзу, а за ней — экран на фокусном расстоянии от линзы. Линза фокусирует лучи, идущие параллельно, в одной точке (в фокусе). В этой точке волны складываются и взаимно усиливаются. Углы φ, удовлетворяющие условию, определяют положение так главных максимумов на экране (соответствующих 1, 2 и т.д. порядку).

Наряду с картиной, получаемой в результате дифракции света, в случае дифракционной решетки наблюдается дифракционная картина и от отдельных щелей. Интенсивности максимумов в ней меньше интенсивности главных максимумов. Так как положение максимумов (кроме центрального, соответствующего k = 0) зависит от длины волны, то решетка разлагает белый свет в спектр. Чем больше λ, тем дальше от центрального максимума располагается тот или иной максимум, соответствующий данной длине волны.

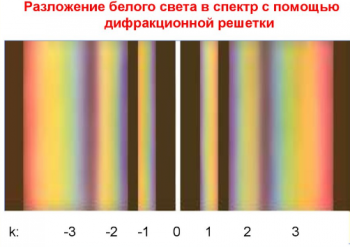
Каждому значению k соответствует свой порядок спектра. Между максимумами расположены минимумы освещенности. Чем больше число щелей, тем более резко очерчены максимумы и тем более широкими минимумами они разделены.

Пример №1. В опыте Юнга по дифракции расстояние между щелями равно d = 7∙10 –4 м. Расстояние от двойной щели до экрана равно D = 2 м. При освещении прибора зеленым светом расстояние между соседними светлыми дифракционными полосами оказалось равным ∆h = 16∙10 –2 м. Вычислите длину волны.

В некоторой точке С экрана будет наблюдаться максимум освещенности при выполнении условия:

где величина k = 0, 1, 2, … — целые числа.

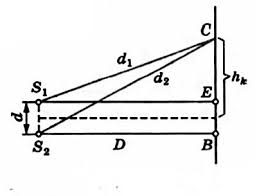
Применим теорему Пифагора к треугольникам S₁CE и S_sCB:

d 2 2 = D 2 + ( h k + d 2 . . ) 2

d 2 1 = D 2 + ( h k − d 2 . . ) 2

Вычитая из первого равенства второе, получаем:

d 2 2 − d 2 1 = 2 h k d

( d 2 + d 1 ) ( d 2 − d 1 ) = 2 h k d

Так как расстояние между щелями много меньше расстояния между ними и экраном, то можем считать, что:

d 2 − d 1 ≈ h k d D . .

Учитывая, что d 2 − d 1 = k λ , можем считать, что:

Отсюда можем найти расстояние k-той светлой полосы от центра экрана:

Расстояние между соседними полосами равно:

Δ h = h k + 1 − h k ≈ λ D d . .

λ ≈ d Δ h D . . ≈ 7 · 10 − 4 · 16 · 10 − 2 2 . . = 56·1 0 − 6 ( м ) = 56 ( м к м )

На плоскую непрозрачную пластину с узкими параллельными щелями падает по нормали плоская монохроматическая волна из красной части видимого спектра. За пластиной на параллельном ей экране наблюдается интерференционная картина, содержащая большое число полос. При переходе на монохроматический свет из синей части видимого спектра

а) расстояние между интерференционными полосами увеличится

б) расстояние между интерференционными полосами уменьшится

в) расстояние между интерференционными полосами не изменится

г) интерференционная картина станет невидимой для глаза

Алгоритм решения

1. Записать, как зависит расстояние между интерференционными полосами от частоты световых лучей.
2. Выбрать ответ, удовлетворяющий установленной зависимости.

Решение

Зависимость расстояния между интерференционными полосами от частоты световых лучей удалось установить экспериментально. Было выяснено, что чем выше частота, тем меньше расстояние между ними. Частота света из синего части спектра больше частоты из красной части спектра. Поэтому при переходе из красной части спектра в синюю часть расстояние между полосами интерференционной картины уменьшится.

pазбирался: Алиса Никитина | обсудить разбор | оценить

В прозрачном сосуде, заполненном водой, находится дифракционная решётка. Решётка освещается лучом света лазерной указки, падающим перпендикулярно её поверхности через боковую стенку сосуда. Как изменятся частота световой волны, длина волны, падающей на решётку, и угол между падающим лучом и первым дифракционным максимумом при удалении воды из сосуда?

Для каждой величины определите соответствующий характер изменения:

1. Увеличится
2. Уменьшится
3. Не изменится

Запишите в таблицу выбранные цифры для каждого ответа. Цифры в ответе могут повторяться.

Алгоритм решения

Решение

Когда воды в сосуде не станет, изменится оптическая плотность среды — ею будет воздух, имеющий абсолютный показатель преломления 1 (у воды он равен 1,33).

Частота световой волны — величина постоянная. Она не меняется при изменении любых величин.

Длина световой волны меняется с учетом оптической плотности среды. Она определяется формулой:

В оптически более плотной среде скорость распространения волны уменьшается. Но когда их сосуда была удалена вода, оптическая плотность уменьшилась, значит, скорость волны увеличилась. Так как частота волны — постоянная, а длина волны прямо пропорциональна ее скорости, то при увеличении скорости длина волны тоже увеличится.

В оптически более плотной среде волны отклоняются от прямолинейного распространения сильнее в сторону нормали. Поэтому при удалении воды, когда оптическая среда станет менее плотной, лучи отклонятся от нормали. В этом случае угол между нормалью к решётке и первым дифракционным максимумом увеличится.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Дифракционная решётка с периодом 10 –5 м расположена параллельно экрану на расстоянии 0,75 м от него. На решётку по нормали к ней падает пучок света с длиной волны 0,4 мкм. Какого порядка максимум в спектре будет наблюдаться на экране на расстоянии 3 см от центра дифракционной картины? Считать sina ≈ tga.

Как используется солнечная энергия

1. Где используют солнечную энергию?
2. Использование солнечной энергии: особенности
3. Пассивные системы
4. Активные системы
5. Фотоэнергия
6. Солнечные фотоэлементы
7. Солнечные коллекторы
8. Солнечные батареи
9. Материалы
10. Преимущества солнечных установок

Что мы знаем про использование солнечной энергии на земле и про ее перспективы? Все мы, даже не имея дома солнечных батарей, активно пользуемся энергией солнца. Так, оно нагревает своим теплом нашу планету и не дает нам умереть от холода, осветляет поверхность Земли. Задумайтесь: всего один квадратный километр способен излучить почти 63000 кВт энергии. Чтобы понять, сколько это, представьте, что это равно работе целого миллиона электрических лампочек! Таким образом, каждую секунду солнце излучает 80 000 миллиардов кВт. Впечатляющие цифры.

Без энергии всего человечества попросту бы не существовало. Вспомним школьные годы и закон сохранения энергии, который мы изучали на уроках физики: энергия не возникает из ниоткуда и не может исчезнуть бесследно. Ее можно получить из природных ресурсов. Например, из угля, природного газа или урана. Ее превратят в необходимое нам тепло или свет. И все же, главным источником энергии было и остается солнце.

Разумеется, человеку было бы глупо не воспользоваться солнечной энергией, как альтернативой электрической, поскольку она имеет ряд преимуществ. Во-первых, она самовозобновляема, то есть участие человека абсолютно не требуется, во-вторых, бесплатна, в-третьих, может использоваться для нужд как мощных заводов, в хозяйстве, так и в быту среднестатистического пользователя, в-четвертых, безопасна для окружающей среды и здоровья человека. Чем ближе местность к югу, тем перспективнее использование солнечных батарей. Так, к примеру, в Израиле около 90 % домов имеют подобное оборудование.

Узнайте больше о самовозобновляемой и бесплатной энергии будущего. Солнечные батареи в действии.

Именно поэтому одной из главных задач ученых мира остается изобретение способов максимально полного и эффективного использования энергии большого светила. Поистине, это будущее всего человечества, ведь природные ресурсы не вечны.

Где используют солнечную энергию?

Год за годом люди все более активно используют энергию солнца. Если еще пять лет тому назад ее использовали для подогрева воды на даче, например, то сейчас возобновляемый источник энергии используют повсеместно промышленные объекты, а также пользователи для освещения своих домов и подогрева воды.

Использование солнечной энергии — ключевые сферы:

• В аграрном хозяйстве: для электрообеспечения парников ангаров и т.п.
• На спортивных объектах: для электроснабжения.
• В медицинских учреждениях: для энергоснабжения и автономности от перепадов напряжения и плановых отключений электричества.
• В авиации и космической промышленности.
• Для уличного освещения в городах.
• Для электрификация отдаленных населенных пунктов.
• В жилых домах: для их электроснабжение, отопление и снабжение горячей водой.
• Для бытовых нужд.

Солнечные панели в авто — Honda Fit

Использование солнечной энергии: особенности

Для превращения излучаемого солнцем света в тепловую энергию используют пассивные и активные системы. Как их различать? Пассивные системы – это здания, которые построены с применением таких стройматериалов, которые максимально эффективно поглощают солнечную энергию. Активные же – это коллекторы, фотоэлементы и солнечные батареи.

Пассивные системы

Как уже упомянуто выше, это так называемые «солнечные здания». Их строят, учитывая особенности климатической зоны, в которой они расположены. Материалы, из которых они строятся, дают возможность использования всей солнечной энергии для освещения, обогрева, охлаждения помещений. Как жилых, так и промышленных. Что же это за материалы и технологии? Это изоляция, деревянный пол, поглощающий свет от поверхности, расположение здания фасадом к югу.

Построенные таким образом солнечные здания максимально используют солнечное излучение, к тому же довольно быстро окупаются, снижая энергозатраты пользователей. Счастливые обладатели таких домов становятся энергетически независимы, а также живут в экологически чистых условиях.

Активные системы

В данную подкатегорию входят коллекторы, солнечные батареи, аккумуляторы, насосы, трубопроводы для горячей воды и теплоснабжения. Их располагают на крышах или в подвалах.

Фотоэнергия

Это один из способов использования излучения солнца: постоянный ток, который вырабатывается при попадании солнечного излучения. Это преобразование происходит в фотоячейках. Фотоячейки имеют двухслойную структуру. Один полупроводник располагается ниже и относится к р-типу, второй находится выше и относится к n-типу.

Электроны второго проводника поглощают излучение солнечной энергии, после чего покидают орбиты, переходя в зону первого проводника. Именно в этот момент появляется электронный поток – фототок.

Солнечные фотоэлементы

Используются они для более эффективного применения солнечного излучения. Они состоят из полупроводников, которые, при попадании на их поверхность солнечных лучей, приходят в движение и таким образом вырабатывают ток. Из-за отсутствия химических реакций при выработке тока, срок их службы достаточно долгий. Один из способов использования это фотоэлемент для включения света.

Фотоэлектрические преобразователи энергии солнца легки в использовании благодаря маленькому весу, легкостью в обслуживании. К тому же, являются очень эффективными при использовании энергии солнца.

Солнечные коллекторы

Принцип их работы заключается в преобразовании солнечного излучения в тепло. Коллекторы можно разделить на группы:

• Вакуумные.Используются в быту, когда вам нужна горячая вода. Состоят из стеклянных трубочек, которые нагреваются от солнечных лучей. В свою очередь, они уже нагревают воду.
• Плоские. Довольно распространены среди пользователей альтернативных источников энергии. Удобны в использовании для бытовых отопительных потребностей, а также для подогрева воды.
• Интегрированные. Считаются наиболее простыми и используются в газовых котлах для подогрева воды. Подогретая вода накапливается в баке для последующего потребления.
• Воздушные. Предназначены для воздушного отопления, рекуперации воздушных масс и для осушительных установок.

Для того, чтобы в последующем использовать солнечную энергию, вначале коллекторы накапливают ее в модулях, которые ставятся на крыше. Их конструкция следующая: это стеклянные трубки и пластины, окрашенные в черный цвет для лучшего поглощения излучения солнца.

Солнечные батареи

Что такое солнечная батарея? Давайте разбираться. Она состоит из модулей, которые принимают и преобразуют энергию солнца, в том числе тепловую. Батареи генерируют электрическую энергию постоянно либо аккумулируют ее для дальнейшего использования.Чаще всего используют солнечные батареи с помощью аккумуляторов – химических источников тока. Первое их применение зафиксировано в космическом спутнике.

Материалы

Для производства большинства батарей используют кремний, который стоит недешево. Потому первичная покупка влетит вам в копеечку, что впрочем, окупится за несколько лет. У солнечных батарей множество достоинств. Это простота конструкции батарей, легкость в установке, нетребовательность в обслуживании, долгая эксплуатация, эргономичность. Работают они от аккумуляторов. Главное, о чем не стоит забывать: они должны работать на открытых участках, не затемненных деревьями или зданиями. Также не рекомендуют забывать об очищении батарей от пыли и прочих загрязнений. При правильной эксплуатации солнечных батарей, они прослужат вам верой и правдой не один десяток лет. Энергию они вырабатывают как в течение светового дня, так и при пасмурных погодных условиях. Последнее время цена батарей неуклонно падает, что говорит про перспективы их использования.

Преимущества солнечных установок

Конечно же, стоит отметить явные достоинства таких установок:

• Они неисчерпаемы, потому никогда не закончатся.
• Абсолютно бесплатно потребляют солнечную энергию.
• Очень безопасны в эксплуатации.
• Обладают таким качеством, как автономность, так как работают от аккумуляторов.
• Крайне экономичны, ведь потратитесь вы только раз, приобретая их.
• Вы независимы от скачков напряжения в электросети или от плановых отключений.
• Установки долговечны при правильной эксплуатации.
• Довольно просты как в использовании, так и в их обслуживании.

Мы неспроста закончили статью преимуществами солнечных установок, ведь благодаря ним, они с каждым годом становятся всё популярнее. Неудивительно: вы хорошенько сэкономите, купив такое чудо техники, а еще защитите свою семью и их здоровье, ведь установки не наносят ни малейшего вреда человеку, а солнечная энергия практически вечная и бесплатная. Использование солнечной энергии – поистине наше светлое будущее! А перспективы безграничны.

Похожие записи:

1. Ассортимент – понятие, структура, виды и свойства
2. Цунами – определение, причины возникновения, предвестники и виды
3. Дефекты в кристаллах – все виды с подробным описанием
4. Звуковые волны определение, виды, основные свойства и характеристики