Метод интервалов, решение неравенств

О чем эта статья:
Определение квадратного неравенства
Неравенство — алгебраическое выражение, в котором используются знаки ≠, , ≤, ≥.
Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения.
Решение — значение переменной, при котором неравенство становится верным.
Решить неравенство значит найти множество, для которых оно выполняется.
Квадратное неравенство выглядит так:
 |
где x — переменная,
Квадратное неравенство можно решить двумя способами:
- графический метод;
- метод интервалов.
Решение неравенства графическим методом
При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax^2 + bx + c = 0. Чтобы найти корни, нужно найти дискриминант данного уравнения.
Как дискриминант влияет на корни уравнения:
- D = 0. Если дискриминант равен нулю, тогда у квадратного уравнения есть один корень;
- D > 0. Если дискриминант больше нуля, тогда у квадратного уравнения есть два корня;
- D
Решение неравенства методом интервалов
Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств.
Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция. При этом знак может быть любым: >, или ≥ — наносим штриховку над промежутками со знаками +.
Плюс или минус: как определить знаки
Можно сделать вывод о знаках по значению старшего коэффициента a:
если a > 0, последовательность знаков: +, −, +,
если a 0, последовательность знаков: +, +,
если a 0 имеет два корня, то знаки его значений на промежутках чередуются. Это значит, что достаточно определить знак на одном из трех промежутков и расставить знаки над оставшимися промежутками, чередуя их. В результате возможна одна из двух последовательностей: +, −, + или −, +, −.
Теперь мы знаем пошаговый алгоритм. Чтобы закрепить материал потренируемся на примерах и научимся использовать метод интервалов для квадратных неравенств.
Пример 1. Решить неравенство методом интервалов: x^2 – 5x + 6 ≥ 0.
Разложим квадратный трехчлен на множители.
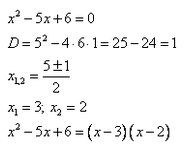
Неравенство примет вид:
Проанализируем два сомножителя:
Первый: х – 3. Этот сомножитель может поменять знак при х = 3, значит при х 0 принимает положительные значения: х – 3 > 0.
Второй: х – 2. Для этого сомножителя такая «знаковая» точка: х = 2.
Вывод: знак произведения (х – 3) * (х – 2) меняется только при переходе переменной через значения х = 3 и х = 2.
В этом весь смысл метода интервалов: определить интервалы значений переменной, на которых ситуация не меняется и рассматривать их как единое целое.
Отобразим эти данные на чертеже:

2 3 — на этом интервале ситуация не изменяется. Значит нужно взять любое значение из этого интервала и подставить его в произведение. Например: х = 25.
- (25 – 3) (25 – 2) = 22*23 = 506 > 0
Вывод: при х > 3 верно неравенство (х – 3) * (х – 2) > 0. Внесем эти данные в чертеж.
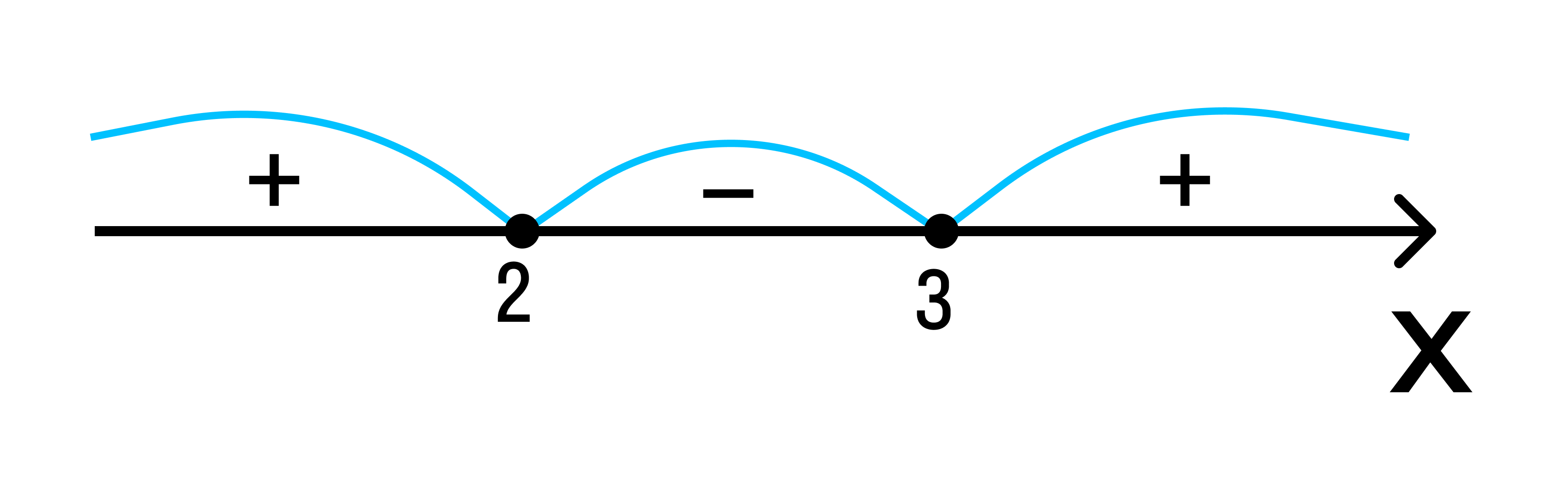
Исходное неравенство: (х – 3) * (х – 2) ≥ 0.
Если (х – 3) * (х – 2) > 0:
Если (х – 3) (х – 2) = 0 — при х1 = 3, х2 = 2.
Удовлетворяющие неравенству точки закрасим, а не удовлетворяющие — оставим пустыми.

Ответ: х ≤ 0, х ≥ 3.
Пример 2. Применить метод интервалов для решения неравенства х2+4х+3
Таблица числовых промежутков: виды, обозначения, изображения
Среди множеств чисел имеются множества, где объектами выступают числовые промежутки. При указывании множества проще определить по промежутку. Поэтому записываем множества решений, используя числовые промежутки.
Данная статья дает ответы на вопросы о числовых промежутках, названиях, обозначениях, изображениях промежутков на координатной прямой, соответствии неравенств. В заключение будет рассмотрена таблица промежутков.
Виды числовых промежутков
Каждый числовой промежуток характеризуется:
- названием;
- наличием обычного или двойного неравенства;
- обозначением;
- геометрическим изображением на координатой прямой.
Числовой промежуток задается при помощи любых 3 способов из выше приведенного списка. То есть при использовании неравенства, обозначения, изображения на координатной прямой. Данный способ наиболее применимый.
Произведем описание числовых промежутков с выше указанными сторонами:
- Открытый числовой луч. Название связано с тем, что его опускают, оставляя открытым.
Этот промежуток имеет соответствующие неравенства x a или x > a , где a является некоторым действительным числом. То есть на такое луче имеются все действительные числа, которые меньше a – ( x a ) или больше a – ( x > a ) .
Множество чисел, которые будут удовлетворять неравенству вида x a обозначается виде промежутка ( − ∞ , a ) , а для x > a , как ( a , + ∞ ) .
Геометрический смыл отрытого луча рассматривает наличие числового промежутка. Между точками координатной прямой и ее числами имеется соответствие, благодаря которому прямую называем координатной. Если необходимо сравнить числа, то на координатной прямой большее число находится правее. Тогда неравенство вида x a включает в себя точки, которые расположены левее, а для x > a – точки, которые правее. Само число не подходит для решения, поэтому на чертеже обозначают выколотой точкой. Промежуток, который необходим, выделяют при помощи штриховки. Рассмотрим рисунк, приведенный ниже.


Из вышеприведенного рисунка видно, что числовые промежутки соответствуют части прямой, то есть лучам с началом в a . Иначе говоря, называется лучами без начала. Поэтому он и получил название открытый числовой луч.
Рассмотрим несколько примеров.
При заданном строгом неравенстве x > − 3 задается открытый луч. Эту запись можно представить в виде координат ( − 3 , ∞ ) . То есть это все точки, лежащие правее, чем – 3 .
Если имеем неравенство вида x 2 , 3 , то запись ( − ∞ , 2 , 3 ) является аналогичной при задании открытого числового луча.

- Числовой луч. Геометрический смысл в том, что начало не отбрасывается, иначе говоря, луч оставляет за собой свою полноценность.
Его задание идет с помощью нестрогих неравенств вида x ≤ a или x ≥ a . Для такого вида приняты специальные обозначения вида ( − ∞ , a ] и [ a , + ∞ ) , причем наличие квадратной скобки имеет значение того, что точка включена в решение или в множество. Рассмотрим рисунок, приведеный ниже.


Для наглядного примера зададим числовой луч.
Неравенство вида x ≥ 5 соответствует записи [ 5 , + ∞ ) , тогда получаем луч такого вида:

- Интервал. Задавание при помощи интервалов записывается при помощи двойных неравенств a x b , где а и b являются некоторыми действительными числами, где a меньше b , а x является переменной. На таком интервале имеется множество точек и чисел, которые больше a , но меньше b . Обозначение такого интервала принято записывать в виде ( a , b ) . Наличие круглых скобок говорит о том, что число a и b не включены в это множество. Координатная прямая при изображении получает 2 выколотые точки.
Рассмотрим рисунок, приведенный ниже.

Пример интервала − 1 x 3 , 5 говорит о том, что его можно записать в виде интервала ( − 1 , 3 , 5 ) . Изобразим на координатной прямой и рассмотрим.

- Числовой отрезок. Данный промежуток отличается тем, что он включает в себя граничные точки, тогда имеет запись вида a ≤ x ≤ b . Такое нестрогое неравенство говорит о том, что при записи в виде числового отрезка применяют квадратные скобки [ a , b ] , значит, что точки включаются во множество и изображаются закрашенными.

Рассмотрев отрезок, получим , что его задание возможно при помощи двойного неравенства 2 ≤ x ≤ 3 , которое изображаем в виде 2 , 3 . На координатной прямой данный точки будут включены в решение и закрашены.
- Полуинтервалы. Это промежуточные интервалы с включением приграничных точек. Они записываются при помощи двойных неравенств вида a x ≤ b или a ≤ b c , где ( a , b ] и [ a , b ) . Изобразим на координатной прямой.


Если имеется полуинтервал ( 1 , 3 ] , тогда его обозначение можно в виде двойного неравенства 1 x ≤ 3 , при чем на координатной прямой изобразится с точками 1 и 3 , где 1 будет исключена, то есть выколота на прямой.
Таблица числовых промежутков
Промежутки могут быть изображены в виде:
- открытого числового луча;
- числового луча;
- интервала;
- числового отрезка;
- полуинтервала.
Чтобы упростить процесс вычисления, необходимо пользоваться специальной таблицей, где имеются обозначения всех видов числовых промежутков прямой.
Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства.
теория по математике функции
Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.

На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.
Остановимся подробнее на свойствах функций.
Нули функции
Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.
 На рисунке он пересекает ось х при х=-1; х=4; х=6. Эти точки пересечения выделены красным цветом. Внимание!
На рисунке он пересекает ось х при х=-1; х=4; х=6. Эти точки пересечения выделены красным цветом. Внимание!
Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет вид у=k/x, где х не равное 0 число.
График функции у=k/x выглядит следующим образом: 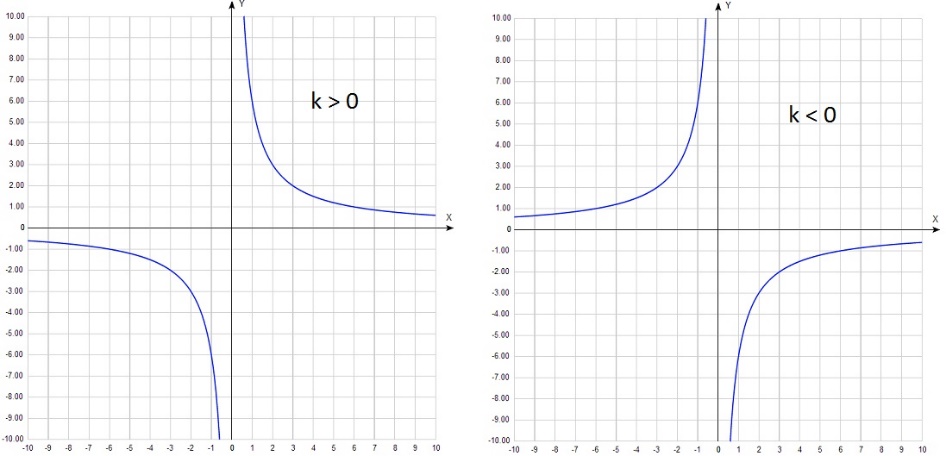 По данному рисунку видно, что нулей функции не существует. Как найти нули функции?
По данному рисунку видно, что нулей функции не существует. Как найти нули функции?
- Для того чтобы найти нули функции, которая задана формулой, надо подставить вместо у число нуль и решить полученное уравнение.
- Если график функции дан на рисунке, то ищем точки пересечения графика с осью х.
Рассмотрим примеры нахождения нулей функции. Пример №1. Найти нули функции (если они существуют):
а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22
Находим х, разделив 22 на 11: х=22:11
Таким образом, мы нашли нуль функции: х=2
б) Аналогично во втором случае. Подставляем вместо у число 0 и решаем уравнение вида 0=(х + 76)(х – 95). Вспомним, что произведение двух множителей равно 0 тогда и только тогда, когда хотя бы один из множителей равен 0. Таким образом, так как у нас два множителя, составляем два уравнения: х + 76 = 0 и х – 95 = 0. Решаем каждое, перенося числа 76 и -95 в правую часть, меняя знаки на противоположные. Получаем х = – 76 и х = 95. Значит, нули функции это числа (-76) и 95.
в) в третьем случае: если вместо у подставить 0, то получится 0 = – 46/х, где для нахождения значения х нужно будет -46 разделить на нуль, что сделать невозможно. Значит, нулей функции в этом случае нет.
Пример №2. Найти нули функции у=f(x) по заданному графику.

Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.
Промежутки знакопостоянства
Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.

Рассмотрим по нашему рисунку, на какие промежутки разбивается область определения данной функции [-3; 7] ее нулями. По графику видно, что это 4 промежутка: [-3; -1), (-1;4), (4; 6) и (6; 7]. Помним, что значения из области определения смотрим по оси х.
На рисунке синим цветом выделены части графика в промежутках [-3; -1) и (4; 6), которые расположены ниже оси х. Зеленым цветом выделены части графика в промежутках (-1;4) и (6; 7], которые расположены выше оси х.
Значит, что в промежутках [-3; -1) и (4; 6) функция принимает отрицательные значения, а в промежутках (-1;4) и (6; 7] она принимает положительные значения. Это и есть промежутки знакопостоянства.
Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).

Функция принимает положительные значения в промежутках [-2; -1) и (3; 8). Обратите внимание, что эти части на рисунке выделены зеленым цветом.
Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.
Возрастание и убывание функции
Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.

На графике видно, что с увеличением значения х от -3 до 2 значения у тоже увеличиваются. Также с увеличением значения х от 5 до 7 значения у опять увеличиваются. Проще говоря, слева направо график идет вверх (синие линии). То есть в промежутках [-3; 2] и [5; 7] функция у=f(x) является возрастающей.
Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Таблица числовых промежутков: виды, обозначения, изображения.
Среди числовых множеств, то есть множеств, объектами которых являются числа, выделяют так называемые числовые промежутки. Их ценность в том, что очень легко вообразить множество, соответствующее указанному числовому промежутку, и наоборот. Поэтому с их помощью удобно записывать множество решений неравенства.
В этой статье мы разберем все виды числовых промежутков. Здесь мы дадим их названия, введем обозначения, изобразим числовые промежутки на координатной прямой, а также покажем, какие простейшие неравенства им соответствуют. В заключение наглядно представим всю информацию в виде таблицы числовых промежутков.
Навигация по странице.
- Виды числовых промежутков.
- Таблица числовых промежутков.
Виды числовых промежутков
Каждому числовому промежутку присущи четыре неразрывно связанные между собой вещи:
- название числового промежутка,
- отвечающее ему неравенство или двойное неравенство,
- обозначение,
- и его геометрический образ в виде изображения на координатной прямой.
Любой числовой промежуток может быть задан любым из трех последних по списку способов: либо неравенством, либо обозначением, либо его изображением на координатной прямой. Причем по данному способу задания, например, по неравенству, с легкостью восстанавливаются и другие (в нашем случае обозначение и геометрический образ).
Переходим к конкретике. Опишем все числовые промежутки с указанных выше четырех сторон.
Начнем с описания числового промежутка, получившего название открытый числовой луч. Заметим, что часто прилагательное «числовой» опускают, оставляя название открытый луч.
Осталось показать геометрическое изображение открытого луча, из него станет видно, что такое название рассматриваемый числовой промежуток получил не случайно. Обратимся к координатной прямой. Известно, что между ее точками и действительными числами имеет место взаимно однозначное соответствие, что позволяет координатную прямую называть числовой прямой. А при разговоре о сравнении чисел мы отметили, что большее число располагается на координатной прямой правее меньшего, а меньшее – левее большего. Исходя из этих соображений, неравенству x отвечают все точки координатной прямой, лежащие левее точки с координатой a , а неравенству x>a – точки, лежащие правее точки a . Само число a не удовлетворяет этим неравенствам, чтобы подчеркнуть это на чертеже ее изображают точкой с пустым центром. Над точками, которым соответствуют числа, удовлетворяющие неравенству, изображают наклонную штриховку: 
 a”/>
a”/>
Из приведенных чертежей видно, что данным числовым промежуткам соответствуют части числовой прямой, представляющие собой лучи с началом в точке a , но исключая саму точку a . Другими словами, это лучи без начала. Отсюда и название – открытый числовой луч.
Приведем несколько конкретных примеров открытых числовых лучей. Так строгое неравенство x>−3 задает открытый числовой луч. Его же задает запись (−3, ∞) . А на координатной прямой этот числовой промежуток представляет собой множество точек, лежащих правее точки с координатой −3 , не включая саму эту точку. Еще пример: неравенство x , как и запись (−∞, 2,3) , задает открытый числовой луч, который следующим образом изображается на координатной прямой

Переходим к числовым промежуткам следующего вида – числовым лучам. В геометрическом плане их отличие от открытых лучей заключается в том, что начало луча не отбрасывается. Другими словами, геометрический образ числовых промежутков этого вида есть полноценный луч.
Что касается задания числовых лучей с помощью неравенств, то им отвечают нестрогие неравенства x≤a или x≥a . Для них приняты обозначения (−∞, a] и [a, +∞) соответственно, квадратная скобка означают включение записанного рядом с ней числа в множество.

 =a”/>
=a”/>
Для наглядности зададим конкретный числовой луч. Неравенству x≥5 , как и записи [5, +∞) , отвечает множество точек на числовой прямой, представляющее собой луч следующего вида

Переходим к следующему числовому промежутку – интервалу. Интервалы задаются двойными неравенствами вида a , где a и b – некоторые действительные числа, причем a меньше b , а x – переменная. То есть, такой числовой промежуток как интервал представляет собой множество всех таких чисел, которые больше, чем a , но меньше, чем b . Для таких интервалов принято обозначение (a, b) , круглые скобки указывают на то, что ни число a , ни число b не включаются в множество. На координатной прямой интервал представляет собой отрезок прямой, заключенный между точками с координатами a и b , причем эти точки – концы отрезка – не включаются.

Приведем пример интервала: −1 , что то же самое (−1, 3,5) , и изобразим его на координатной прямой

Числовой отрезок – следующий вид числового промежутка – отличается от только что рассмотренного интервала тем, что включает в себя граничные точки. Числовым отрезкам отвечают нестрогие двойные неравенства вида a≤x≤b . В обозначении используются квадратные скобки, в которых через запятую заключены числа a и b : [a, b] . А геометрический образ числового отрезка представляет собой отрезок вместе с его концами:

Например, числовой отрезок, который задается двойным неравенством  можно обозначить как
можно обозначить как  , на координатной прямой ему отвечает отрезок с концами в точках, имеющих координаты корень из двух и корень из трех.
, на координатной прямой ему отвечает отрезок с концами в точках, имеющих координаты корень из двух и корень из трех.
Осталось лишь сказать про числовые промежутки, называемые полуинтервалами. Они представляют собой, если так можно выразиться, промежуточный вариант между интервалом и отрезком, так как включают в себя одну из граничных точек. Полуинтервалы задаются двойными неравенствами a или a≤b , которым соответствуют обозначения (a, b] и [a, b) . Несложно представить и их геометрическую интерпретацию:


Например, полуинтервал (1, 3] можно обозначить как 1 , а на числовой прямой он представлен отрезком с концами в точках с координатами 1 и 3 , причем первую из них следует исключить.
Таблица числовых промежутков
Итак, в предыдущем пункте мы определили и описали следующие числовые промежутки:
- открытый числовой луч;
- числовой луч;
- интервал;
- числовой отрезок;
- полуинтервал.
Для удобства сведем все данные о числовых промежутках в таблицу. Занесем в нее название числового промежутка, соответствующее ему неравенство, обозначение и изображение на координатной прямой. Получаем следующую таблицу числовых промежутков:
Числовые промежутки
Урок 31. Алгебра 8 класс ФГОС


В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности



Конспект урока “Числовые промежутки”
Как вы уже знаете, любое число можно отметить точкой на координатной прямой. Верно и обратное утверждение: каждой точке на координатной прямой соответствует какое-то число.
Также на координатной прямой можно отметить и множество чисел х, удовлетворяющих любому неравенству. Такое множество называют числовым промежутком. И в зависимости от типа неравенства выделяют виды числовых промежутков, которые имеют свои названия, обозначения и изображения на координатной прямой.
Вспомним типы неравенств.
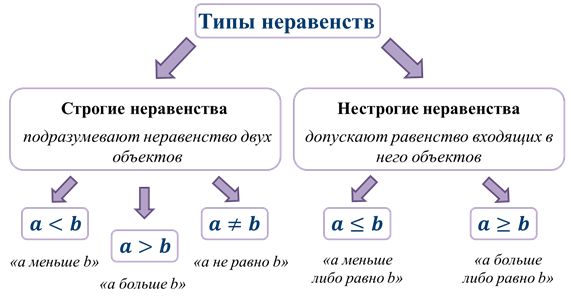
Рассмотрим виды числовых промежутков на конкретных примерах.
Пусть есть два числа: 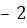 и
и  .
.

Множество всех чисел, удовлетворяющих условию 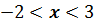 называют интервалом.
называют интервалом.

Множество всех чисел, удовлетворяющих условию  называют числовым отрезком.
называют числовым отрезком.
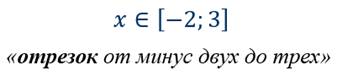
Множества чисел 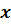 , для которых выполняются двойные неравенства
, для которых выполняются двойные неравенства 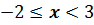 или
или  , называют полуинтервалами.
, называют полуинтервалами.
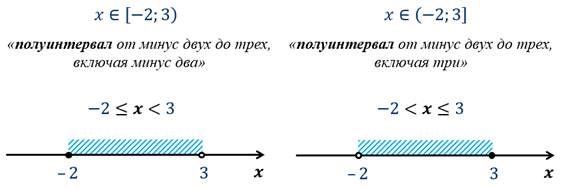
На экране вы видите, как изображают такие полуинтервалы на координатной прямой.

Как вы уже знаете, множество действительных чисел изображается всей координатной прямой. Его называют числовой прямой и обозначают так:
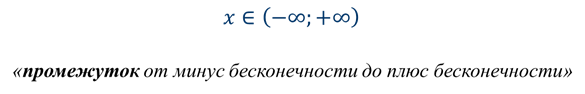
Рассмотрим другие виды числовых промежутков.
Множество чисел, удовлетворяющих условию 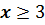 называют числовым лучом.
называют числовым лучом.
Множество чисел, удовлетворяющих условию 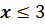 называют числовым лучом.
называют числовым лучом.
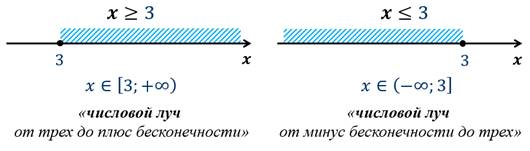
Множества чисел, удовлетворяющих условиям 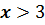 или
или 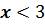 называют открытым числовым лучом.
называют открытым числовым лучом.
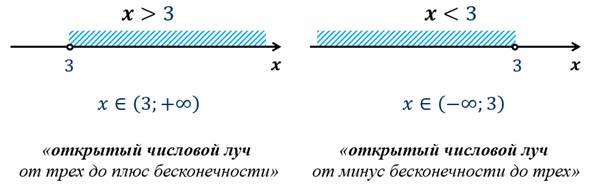
Заметим, что в обоих случаях число 3 не входит в множества.
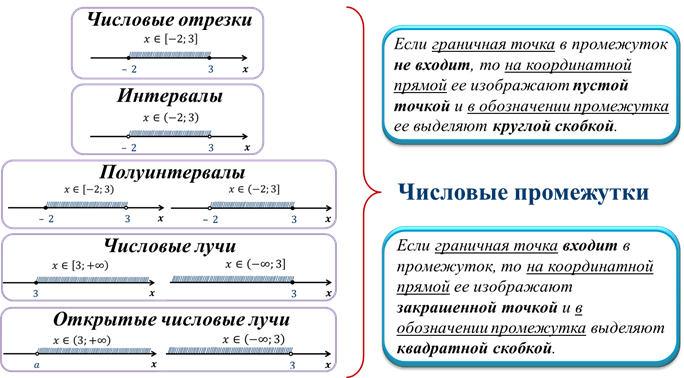
Числовые отрезки, интервалы, полуинтервалы, числовые лучи и открытые числовые лучи называют числовыми промежутками.
Замечание: Если граничная точка в промежуток не входит, то на координатной прямой её изображают пустой точкой и в обозначении промежутка её выделяют круглой скобкой. Если же граничная точка входит в промежуток, то на координатной прямой её изображают закрашенной точкой и в обозначении промежутка выделяют квадратной скобкой.
Запишем обозначения числовых промежутков, их названия и изображение на координатной прямой для произвольных чисел 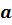 и
и  .
.

Задание: изобразить на координатной прямой множество чисел, удовлетворяющих неравенствам, и записать решение числовым промежутком.
Решение:

Задание: найдём все целые числа, удовлетворяющие неравенствам.
Решение:
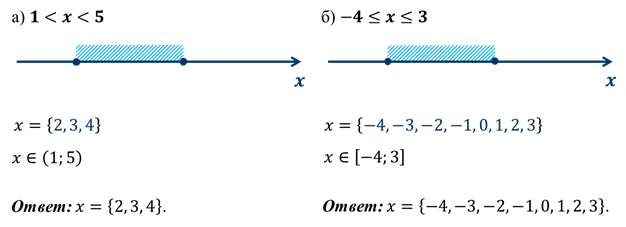
Имея представления о числовых промежутках можно находить их пересечение и объединение.
Например: найдём пересечение и объединение числовых промежутков:
Решение:
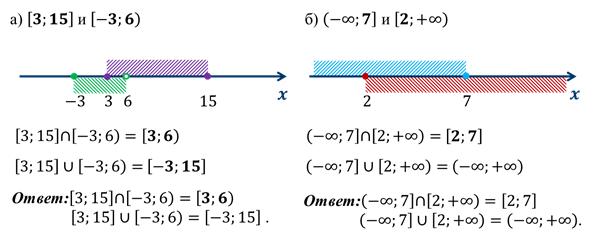
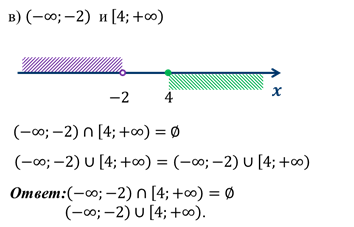
Интервал – это множество чисел, удовлетворяющих условию или Оцените видеоурок
∑ Некоторые алгебраические понятия – определения и работа с ними
Числовые промежутки. Контекст. Определение
Равенство (уравнение) имеет одну точку на числовой прямой (хотя это точка зависит от проделанных преобразований и выбранного корня). Само решение уравнения будет числовым множеством (иногда состоящим из одного числа). Однако, всё это на числовой прямой (визуализации множества вещественных чисел) будет отображаться лишь точечно, но существуют также более обобщённые типы отношений между двумя числами – неравенства. В них числовая прямая разделяется некоторым числом и от неё отсекается определённая часть – значения выражения или числовой промежуток.
Тему числовых промежутков логично обсуждать вместе с неравенствами, но это отнюдь не означает, что она связана лишь с ними. Числовые промежутки (интервалы, отрезки, лучи) являются множеством значений переменной, удовлетворяющих некоему неравенству. То есть, по сути, это множество всех точек на числовой прямой, ограниченной какими-то рамками. Поэтому наиболее тесно связана тема числовых промежутков с понятием переменной. Там, где есть переменная, или произвольная точка x на числовой прямой, и её применяют, используют, есть и числовые промежутки, интервалы – значения x. Часто значение может быть любым, но это тоже числовой промежуток, охватывающий всю числовую прямую.
Введём понятие числового промежутка. Среди числовых множеств, то есть множеств, объектами которых являются числа, выделяют так называемые числовые промежутки. Их ценность в том, что очень легко вообразить множество, соответствующее указанному числовому промежутку, и наоборот. Поэтому с их помощью удобно записывать множество решений неравенства. Тогда как множеством решения уравнения будет не числовой промежуток, а просто несколько чисел на числовой прямой, с неравенствами, иначе говоря, любыми ограничениями значения переменной появляются числовые промежутки.
– это множество всех точек числовой прямой, ограниченное данным числом или числами (точками на числовой прямой).
Числовой промежуток любого вида (множество значений x, заключённых между некоторыми числами) всегда можно представить тремя видами математических обозначений: специальными обозначениями промежутков, цепочками неравенств (одним неравенством или двойным неравенством) или геометрически на числовой прямой. По сути, все эти обозначения имеют один смысл. Они дают ограничение(-я) для значений какого-то математического объекта, переменной величины (некоторой переменной, любого выражения с переменной, функции и т.д.).
Из вышесказанного можно понять, что так как можно по-разному ограничить область числовой прямой (есть разные типы неравенств), то и типы числовых промежутков бывают разные.
Виды числовых промежутков
Каждый тип числового промежутка имеет собственное название, особое обозначение. Для обозначения числовых промежутков используют круглую и квадратную скобку. Круглая скобка означает, что конечная, определяющая границу, точка на числовой прямой (конец) у этой скобки не входит во множество точек данного промежутка. Квадратная скобка означает, что конец входит в промежуток. С бесконечностью (с этой стороны промежуток не ограничен) используют круглую скобку. Иногда вместо круглых скобок можно писать квадратные, повёрнутые в обратную сторону: (a;b) ⇔]a;b[
| Вид промежутка (название) | Геометрическое изображение (на числовой прямой) | Обозначение | Запись с помощью неравенств (для краткости всегда цепочками) |
|---|---|---|---|
| Интервал (открытый) | (a;b) | a x x ≤ b | |
| Полуинтервал (полусегмент) | [a;b) | a ≤ x x ≤ b | |
| Луч | [a;+∞) | x ≥ a | |
| Луч | (-∞;b] | x ≤ b | |
| Открытый луч | (a;+∞) | x > a | |
| Открытый луч | (-∞;b) | x x ∈ ℝ (обычно говорят о множестве вещественных чисел, для представления комплексных чисел используют уже комплексную плоскость, а не прямую) | |
| Равенство | [a;a] или x=a | x = a (частный случай нестрогого неравенства: a ≤ x ≤ a – интервал длины 1, где оба конца совпадают – отрезок, состоящий из одной точки) | |
| Пустое множество | ∅ | Пустое множество тоже является промежутком – у переменной x нет значений (пустое множество). Обозначение: x∈∅⇔x∈ . |
С названиями промежутков может возникнуть путаница: есть огромное количество вариантов. Поэтому лучше всегда точно их указывать. В англоязычной литературе используется только термин интервал (“interval”) – открытый, замкнутый, полуоткрытый (полузамкнутый). Вариаций много.
С помощью промежутков в математике обозначается очень большое количество вещей: есть промежутки изоляции при решении уравнений, промежутки интегрирования, промежутки сходимости рядов. Промежутками принято всегда обозначать при при исследовании функции её область значений и область определения. Промежутки очень важны, например, есть теорема Больцано — Коши (можно узнать больше в “Википедии”).
Системы и совокупности неравенств
Система неравенств
Итак, переменную x или значение некоторого выражения можно сравнить с какой-то постоянной величиной – это неравенство, но можно сравнивать это выражение с несколькими величинами – двойное неравенство, цепочка неравенств и т. д. Именно это было показано выше – как интервал и отрезок. И то, и то является системой неравенств.
Итак, если ставится задача найти множество общих решений двух или больше неравенств, то можно говорить о (также как с уравнениями — хотя можно сказать, что уравнения – это частный случай).
Тогда очевидно, что значение переменной, использованной в неравенствах, при котором каждое из них обращается в верное, называется .
Решение систем линейных неравенств с одной переменной в общем случае сводится к вот этим 4 видам: x > a x > b (1) x > a x b (2) x a x > b (3) x a x b (4) . Здесь предполагается, что b > a.
Любую систему можно решать графически с использованием числовой прямой. Там, где решения составляющих систему неравенств пересекаются и будет решение самой системы.
Представим для каждого случая графическое решение.
(1) x>b
(2) a
(3) x
(4) x∈∅
Итак, что же получается? В случае (1) решением является промежуток (a;+∞). В случае (2) решение – промежуток (a;b). Случай (3) – это пример открытого луча (-∞;a). В случае (4) же решения отдельных неравенств не пересекаются – система не имеет решений.
Далее, системы неравенств можно классифицировать как равносильные, если они имеют общее множество решений. Отсюда (как можно видеть выше) следует, что более сложные системы можно упрощать (например, используя геометрическое решение).
Фигурную скобку можно условно, грубо говоря, назвать эквивалентом союза “И” для неравенств
Совокупность неравенств
Однако, бывают и другие случаи. Так кроме пересечения множеств решений бывает их объединение: если ставится задача найти множество всех таких значений переменной, каждое из которых является решением хотя бы одного из данных неравенств, то говорят, что надо .
Итак, все неравенства в совокупности объединяют скобкой совокупности “[“. Если значение переменной удовлетворяет хотя бы одному неравенству из совокупности, то оно принадлежит множеству решений всей совокупности. Также и с уравнениями (опять же их можно назвать частным случаем).
Если фигурная скобка – и, то скобка совокупности – это, условно, говоря простым языком, эквивалент союза “ИЛИ” для неравенств (хотя это, конечно, будет логическое или, включающее случай, удовлетворяющий обоим условиям).
Итак, – это значение переменной, при котором хотя бы одно неравенство, обращается в верное.
Множество решений, как совокупности, так и системы неравенств, можно определить через две основные бинарные операции для работы с множествами – пересечение и объединение. Множество решений системы неравенств – это пересечение множеств решений неравенств, её составляющих. Множество решений совокупности неравенств – это объединение множеств решений неравенств, её составляющих. Это тоже можно проиллюстрировать. Допустим у нас есть система и совокупность из двух неравенств. Множество решений первого обозначим A, а множество решений второго обозначим B. Прекрасной иллюстрацией будет диаграмма Эйлера-Венна.
A ∪ B – решение системы неравенств
A ∩ B – решение совокупности неравенств fedor1113
К остальным темам 
Числовые промежутки – что такое?
Числовая прямая (или, что то же самое, числовая ось) — понятие нехитрое. Более того, числовая прямая — главный помощник в решении любых заданий с неравенствами! Любых. От примитивных линейных неравенств до сложных показательных или логарифмических неравенств, систем неравенств и метода интервалов. Освоим темку, пока всё просто?)
Что такое числовая прямая? Что такое координатная прямая?
С понятием числовой прямой вы все уже сталкивались, когда изучали такие темы как координаты точек (5-й класс), страшное понятие модуля числа (6-й класс), и особенно когда рисовали графики функций (7-й класс). Вспомним ещё разок?)
Всё то же самое, ничего нового! Первым делом возьмём и нарисуем в тетрадке самую обычную прямую и дополнительно укажем на ней:
1) Начало отсчёта или начало координат (точку О);
2) Положительное направление (стрелочкой);
3) Масштаб или единицу измерения длины (например, одна тетрадная клетка).
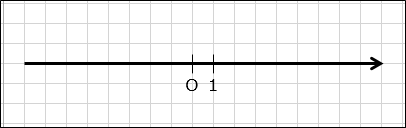
Вот и всё. Про устройство числовой прямой вы тоже давно в курсе (надеюсь). Но на всякий случай напоминаю. Начало координат всегда соответствует числу 0. Все положительные числа изображаются на положительной полуоси справа от нуля, в направлении стрелочки. А все отрицательные — слева от нуля, на отрицательной полуоси. Большее число всегда располагается правее меньшего, а меньшее — левее большего. Элементарно, Ватсон!)
Ну хорошо, прямая и прямая. Но почему — числовая? Ответ очевиден. Каждой точке на прямой соответствует какое-то число. Положительное, отрицательное, целое, дробное, иррациональное — какое угодно. Но — число! Поэтому и прямая — числовая. Это число имеет специальное и вполне научное название — координата точки. Отсюда следует, что числовая прямая — и координатная прямая тоже. Вот так. Два термина в одном флаконе.)
А вот теперь мы с вами колоссально расширяем наши возможности. Начинаем работать с числовой прямой на полную катушку! Готовы?)
Что такое числовой промежуток? Виды числовых промежутков.
В уравнениях было всё просто. Нашли икс, да и записали в ответ. Например, х=2. В неравенствах же ответом обычно служит не одно-два числа, а промежуток. Числовой промежуток. Или даже несколько числовых промежутков. Это и смущает поначалу…) Что это за зверь такой — числовой промежуток?
Числовой промежуток — это просто какой-то кусочек числовой прямой. И всё!
Сейчас начинается самое весёлое. Сейчас мы нашу числовую прямую будем пилить.) Пилить не на дрова, а на… числовые промежутки.)
Вот прям берём числовую прямую и вырезаем из неё какой-то кусочек какими-то точками. Которые, напоминаю, соответствуют каким-то числам. Вот и получаем — числовой промежуток. Разумеется, вырезать конкретный кусочек числовой прямой можно по-разному, да…)
Соответственно, и числовые промежутки в математике бывают разных видов.
Вот они, эти виды (подкрашены красным цветом):
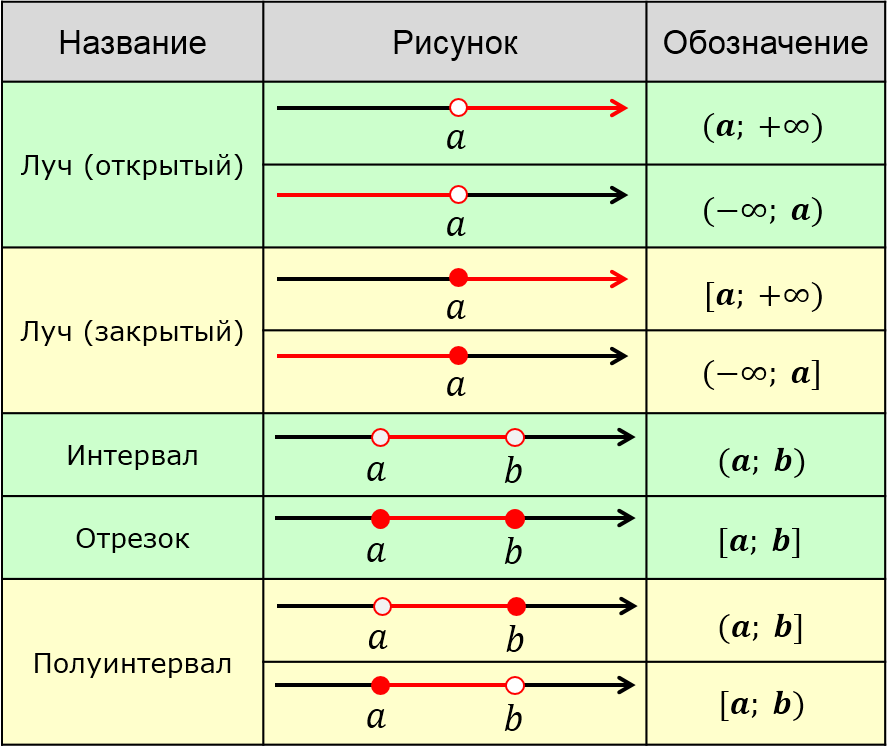
Смотрим на табличку и… мама родная! Какие-то непонятные кружочки (пустые внутри и закрашенные), какой-то странный иероглиф “∞”, да ещё и со знаками плюс/минус, круглые и квадратные скобочки.
Вам и вправду страшно? Возможно… Но сейчас вы увидите, насколько всё просто! Читаем дальше.)
Граничные точки
Я разгадала знак бесконечность… (Земфира)
Те точки, которые нам указывают, в каких местах мы выпиливаем кусочек прямой, так и называются – граничные точки. В таблице эти самые граничные точки обозначены буковками a и b. Точка a — левая граница (меньшее число), точка b — правая граница (большее число).
А может ли числовой промежуток в каком-то направлении быть неограниченным?
А почему — нет? Запросто! Можно распилить числовую прямую не в двух точках, а в какой-то одной точке. И забрать себе одну часть — левую или правую. Бесконечную… Или — луч. Только для обозначения этой бесконечной границы буквы или числа не годятся. Зато есть специальный значок “∞“. Значок этот так и называется — “бесконечность”. Очевидно, бесконечность бывает двух видов (точнее, двух знаков) — плюс (+∞) или минус (-∞). В зависимости от того, какой именно луч, какая часть прямой, правая или левая, берётся на дальнейшее рассмотрение.
Кружочки и скобочки…
Граничная точка — это, как и намекает название, точка, задающая границу числового промежутка. Слева или справа. Естественно, у думающих тут же возникает вполне логичный и важный вопрос: А куда относить саму граничную точку? Включать её в состав промежутка или нет?
Именно для ответа на этот вопрос нам и служат всякие кружочки и скобочки в обозначениях и на рисунках!
Запоминаем:
Если граничная точка в числовой промежуток НЕ ВХОДИТ, то на числовой прямой она рисуется НЕЗАКРАШЕННОЙ. Т.е. пустой внутри. В математике такие точки называются выколотыми точками. В обозначениях выколотые точки всегда соседствуют с круглыми скобками “(” или “)”.
Если же граничная точка в числовой промежуток ВХОДИТ, то на числовой прямой она рисуется ЗАКРАШЕННОЙ, а в записи обозначается квадратной скобкой “[” или “]”.
Вот и вся расшифровка.) Кстати говоря, специальные названия промежутков (луч, отрезок, интервал, полуинтервал) запоминать пока не обязательно. Всё равно поначалу будете путаться. Это для общей эрудиции сделано.) На практике обычно не заморачиваются и говорят “числовой промежуток такой-то…”, без уточнения вида — луч, отрезок и т.д. А иногда и совсем кратко — просто “промежуток”. Если и вы путаетесь — говорите так же. Не ошибётесь! А спецназвания оставим для старших классов. Но если запомнили (и поняли!) названия промежутков — что ж, только респект!)
Теперь можно потренироваться в записи и чтении числовых промежутков. Чтобы не мычать… Ну что, потренируемся?
Читаем числовые промежутки и рисуем их на оси!
С чтением и рисованием числовых промежутков обычно никаких проблем нет. Нужно только чётко понимать, что означают все эти скобочки и кружочки, что разбирались в предыдущем параграфе.
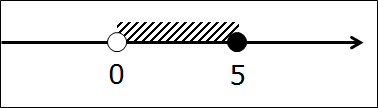
Например, задан числовой промежуток (0; 5].
Словами эта запись звучит так: числовой промежуток от нуля до пяти, не включая ноль и включая пять.
Читаем (и пишем) именно в таком порядке — от левой границы до правой.
Левая граница (т.е. число 0) соседствует с круглой скобкой “(“, о чём нам и говорят слова “не включая”. Этот факт означает, что число 0 в наш промежуток не входит. Например, число 0,1 входит, и даже 0,000001 — ещё входит. Хоть чуть-чуть, да больше нуля. А вот ровно ноль — уже нет…
Пятёрка же — напротив, соседствует с квадратной скобкой “]”, что говорит нам о том, что сама она также входит в наш промежуток. И отражено словом “включая” в словесной расшифровке.
А теперь нарисуем наш промежуток на оси. Для этого рисуем числовую прямую и отмечаем на ней граничные точки 0 и 5.

Заметили разницу между нулём и пятёркой? Ну да, трудно не заметить!  Точка 0 изображена белой, т.е. незакрашенной. Пустой внутри. Или, по-математически, выколотой точкой. Это, как мы с вами уже выяснили, означает, что ноль — не входит в наш промежуток. В отличие от пятёрки, которая входит в промежуток. И на рисунке, соответственно, нарисованной чёрной. Закрашенной.) Я специально точки такими здоровыми изобразил. Чтобы хорошенько врезались в память…
Точка 0 изображена белой, т.е. незакрашенной. Пустой внутри. Или, по-математически, выколотой точкой. Это, как мы с вами уже выяснили, означает, что ноль — не входит в наш промежуток. В отличие от пятёрки, которая входит в промежуток. И на рисунке, соответственно, нарисованной чёрной. Закрашенной.) Я специально точки такими здоровыми изобразил. Чтобы хорошенько врезались в память…
Итак, мы отметили на оси границы промежутка. Осталось лишь отметить все остальные числа, которые входят в этот промежуток. Вы спросите: Как? Ведь между нулём и пятёркой находится бесконечно много чисел! Это и 1, и 2,5, и 3,14, и 4,9999 и так далее… И что? Все-все отмечать)?
Нет, конечно. Всё гораздо проще!) Сейчас мы с вами отметим на прямой все интересующие нас числа одним махом! Тут есть два варианта. Вариант первый — штриховка. Просто берём и подштриховываем весь кусочек прямой между 0 и 5.
Вариант второй рассмотрим на следующем примере.
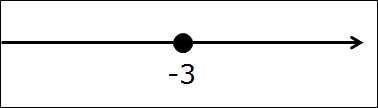
В этот раз дан промежуток такой: [-3; +∞).
Для начала читаем словами название промежутка с гордо поднятой головой: Числовой промежуток от минус трёх до плюс бесконечности, включая минус три!
Вот так. А теперь вопрос на засыпку: почему я оборвал чтение на словах “включая минус три…” и не продолжил мысль гениальными словами “…и не включая плюс бесконечность”?
Всё очень просто. Бесконечность (что плюс, что минус) не может включаться никогда. Это не число, это — символ. Поэтому в подобных записях бесконечность всегда соседствует с круглой скобкой, а в расшифровке говорится просто: “до плюс бесконечности”. Или “до минус бесконечности”. И всё.
А теперь всё как обычно, рисуем прямую, отмечаем на ней одну единственную точку минус три. Закрашенную, естественно, раз уж скобочка перед минус тройкой — квадратная. Вот так:
И отмечаем все остальные числа, входящие в промежуток от минус тройки до плюс бесконечности. На этот раз я отмечу нужный кусок оси дужкой (от слова дуга) вместо штриховки. Вот так:
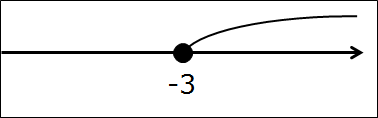
Особой разницы между штриховкой и дужками нет. Рисуйте как удобнее. Но в сложных заданиях с неравенствами, где надо постоянно пересекать и объединять много промежутков, дужки предпочтительнее, ибо штриховка куда менее наглядна. Запутаться можно.
Я предпочитаю совмещать оба способа. Получается красиво и наглядно! В следующем уроке, на примерах, сами увидите.)
Вот так рисуются числовые промежутки на оси.
Входит и выходит… ))
А какая нам разница, входит число в указанный промежуток или не входит?
Вопрос смешной. Огромная! Ответ на этот вопрос (входит/не входит) — это ключевой этап в работе с промежутками и с неравенствами вообще! Даже значки специальные придуманы для этого. Вот такие:
За этими странными значками скрываются безобидные слова “принадлежит” и “не принадлежит”.
Возьмём, к примеру, промежуток (1; 3].
Входит в этот промежуток, допустим, двойка? Конечно! Раз уж она посерёдке между единичкой и тройкой… А единичка? Э-э-э… Скобка перед ней — круглая! Не входит единичка в наш промежуток. Тройка входит? Попадает на границу, но скобочка — квадратная. Значит, входит! А вот три с половиной — снова не входит. 3,5 строго больше, чем тройка. Выпадает 3,5 из нашего промежутка…
Математически, с помощью значков принадлежности, эти факты можно записать вот так:
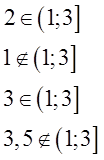
А словами можно прочитать вот так:
Два принадлежит промежутку от одного (не включая) до трёх (включая).
Один не принадлежит промежутку от одного (не включая) до трёх (включая).
В этом уроке было простое чтение и рисование промежутков на оси. Пока — цветочки. Переходим к ягодкам. К операциям над числовыми промежутками. Те ещё грабли, да…) Об этом — в следующем уроке.




