Броуновское движение

О чем эта статья:
7 класс, без форм заявки
Молекулярно-кинетическая теория
Мы состоим из клеток, клетки состоят из молекул, молекулы из атомов, атомы из… Ладно, пока достаточно атомов. И молекулы, и атомы подчиняются законам, которые описаны в молекулярно-кинетической теории.
В основе молекулярно-кинетической теории лежат три основных положения:
- Все вещества — жидкие, твердые и газообразные — образованы из мельчайших частиц: молекул, которые сами состоят из атомов.
Молекулы химического вещества могут быть простыми и сложными, то есть состоять из одного или нескольких атомов. Молекулы и атомы представляют собой электрически нейтральные частицы. При определенных условиях молекулы и атомы могут приобретать дополнительный электрический заряд и превращаться в положительные или отрицательные ионы. - Атомы и молекулы находятся в непрерывном хаотическом движении.
- Частицы взаимодействуют друг с другом силами, которые имеют электрическую природу. Гравитационное взаимодействие между частицами пренебрежимо мало.
Броуновское движение
Во второй половине ХIХ века в научных кругах разгорелась нешуточная дискуссия о природе атомов. На одной стороне дискуссии утверждали, что атомы — просто математические функции, удачно описывающие физические явления и не имеющие под собой реальной физической основы.С другой стороны настаивали, что атомы — это реально существующие физические объекты.
Самое смешное в этих спорах то, что за десять лет до их начала ботаник Роберт Броун уже провел эксперимент, который доказал физическое существование атомов. Вот, как это было:
Как Броун проводил эксперимент
Броун изучал поведение цветочной пыльцы под микроскопом и обнаружил, что отдельные споры совершают абсолютно хаотичные движения.
Представьте себе, что мы издалека наблюдаем, как плотная толпа людей толкает над собой большой мяч. Причём каждый толкает мяч, куда хочет. Мы не видим отдельных игроков, потому что поле далеко от нас, но мяч мы видим — и замечаем, что перемещается он очень беспорядочно.
Мяч постоянно меняет направление своего движения, и пойти в какую-нибудь определенную сторону не желает. Предсказать его местоположение через заданное время — нельзя.
Вот что-то похожее на это Броун увидел при изучении пыльцы.
В первую очередь он начал грешить на движение потоков воды или ее испарение, но проверив эту гипотезу, отмел ее. Проведя множество экспериментов, Броун установил, что такое хаотичное движение свойственно любым микроскопическим частицам — будь то пыльца растений, взвеси минералов или вообще любая измельченная субстанция. Но причины этого явления он выяснить не смог (не в обиду ботаникам, но все же, это не его специализация).
А теперь угадайте, кто смог применить этот эксперимент в доказательстве атомной теории строения вещества. Альберт Эйнштейн, кто же еще. Он объяснил его примерно так: взвешенная в воде спора подвергается постоянной «бомбардировке» со стороны хаотично движущихся молекул воды.
В среднем, молекулы воздействуют на нее со всех сторон с равной интенсивностью и через равные промежутки времени. Однако, как бы ни мала была частица, в силу чисто случайных отклонений сначала она получает импульс со стороны молекулы, ударившей ее с одной стороны, а затем — со стороны молекулы, ударившей ее с другой. И так далее.
Чуть позже, через 3 года после открытия Эйнштейна, в 1908 году французский физик Жан Батист Перрен провел серию опытов, которые подтвердили правильность эйнштейновского объяснения броуновского движения. Стало окончательно ясно, что наблюдаемое «хаотичное» движение броуновских частиц происходит вследствие межмолекулярных соударений. Поскольку вывод о том, что несуществующие в природе математические функции не могут привести к физическому взаимодействию, напрашивается сам собой, стало окончательно ясно, что спор о реальности атомов окончен: они существуют в природе.
Также, если еще раз посмотреть на второе положение молекулярно-кинетической теории, можно заметить, что броуновское движение очень хорошо его доказывает: Атомы и молекулы находятся в непрерывном хаотическом движении.
Диффузия
Явление, которое доказывает первое и второе положения молекулярно-кинетической теории называется диффузия.
- Диффузия — это взаимное проникновение частиц одного вещества в другое, обусловленное движением молекул.
Диффузия в газах
Если в комнате открыть флакон с духами или зажечь ароматизированную свечу, то запах вскоре будет чувствоваться во всей комнате. Распространение запахов происходит из-за того, что молекулы духов проникают между молекулами воздуха. На самом деле, в этом процессе очень большую роль играет такой вид теплопередачи, как конвекция, но и без диффузии не обошлось.
На самом деле, молекулы вокруг нас движутся очень быстро — со скоростью в сотни метров в секунду — это напрямую зависит от температуры.
Давайте проверим это сами несложным экспериментом:
Замерьте температуру воздуха в помещении. Распылите освежитель воздуха в одном углу, встаньте в другой и включите секундомер. А лучше проведите эксперимент вдвоем, чтобы один человек распылял, а другой включал секундомер — так не будет погрешности, но будет веселье 
Как только почувствуете аромат освежителя в противоположном от места распыления, выключите секундомер. Запишите результат измерения. А потом проветрите помещение и проделайте все то же самое. Время, через которое до вас дойдет запах, будет другим. Во втором случае аромат будет распространяться медленнее.
То есть, чем выше температура, тем больше скорость диффузии.
Диффузия в жидкостях
Если диффузия в газах происходит быстро — чаще всего за считанные секунды — то диффузия в жидкостях занимает минуты или в некоторых случаях часы. Зачастую это зависит от температуры (как и в эксперименте выше) и плотности вещества.
С диффузией в жидкостях вы встречаетесь, когда, например, размешиваете краску. Или когда смешиваете любые две жидкости, например, газировку с сиропом. Также из-за диффузии происходит загрязнение рек (да и в целом окружающей среды).
Ну или вот пример диффузии в жидкостях, с которым вы точно не встречались — акулы ищут свою жертву по запаху крови, который распространяется в океане за счет диффузии.
Диффузия в твёрдых телах
Диффузия в твёрдых телах происходит очень медленно. Например, при комнатной температуре (около 20 °С) за 4-5 лет золото и свинец взаимно проникают друг в друга на расстояние около 1 мм.
Кстати, если вы проведете такой эксперимент, то увидите, что в свинец проникло малое количество золота, а свинец проник в золото на глубину не более одного миллиметра. Такое различие обусловлено тем, что плотность свинца намного выше плотности золота.
Этот процесс можно ускорить за счет нагревания, как в жидкостях и газах. Если на тонкий свинцовый цилиндр нанести очень тонкий слой золота, и поместить эту конструкцию в печь на неделю при температуре воздуха в печи 200 градусов Цельсия, то после разрезания цилиндра на тонкие диски, очень хорошо видно, что свинец проник в золото и наоборот.
Броуновское движение
Содержание
Что такое броуновское движение?
Сейчас вы познакомитесь с самым очевидным доказательством теплового движения молекул (второе основное положение молекулярно-кинетической теории). Обязательно постарайтесь посмотреть в микроскоп и увидеть, как движутся так называемые броуновские частицы.
Ранее вы узнали, что такое диффузия, т. е. перемешивание газов, жидкостей и твердых тел при их непосредственном контакте. Это явление можно объяснить беспорядочным движением молекул и проникновением молекул одного вещества в пространство между молекулами другого вещества. Этим можно объяснить, например, тот факт, что объем смеси воды и спирта меньше объема составляющих ее компонентов. Но самое очевидное доказательство движения молекул можно получить, наблюдая в микроскоп мельчайшие, взвешенные в воде частицы какого-либо твердого вещества. Эти частицы совершают беспорядочное движение, которое называют броуновским.
Броуновское движение – это тепловое движение взвешенных в жидкости (или газе) частиц.
Наблюдение броуновского движения
Английский ботаник Р. Броун (1773-1858) впервые наблюдал это явление в 1827 г., рассматривая в микроскоп взвешенные в воде споры плауна. Позже он рассматривал и другие мелкие частицы, в том числе частички камня из египетских пирамид. Сейчас для наблюдения броуновского движения используют частички краски гуммигут, которая нерастворима в воде. Эти частички совершают беспорядочное движение. Самым поразительным и непривычным для нас является то, что это движение никогда не прекращается. Мы ведь привыкли к тому, что любое движущееся тело рано или поздно останавливается. Броун вначале думал, что споры плауна проявляют признаки жизни.
Броуновское движение – тепловое движение, и оно не может прекратиться. С увеличением температуры интенсивность его растет. На рисунке 8.3 приведена схема движения броуновских частиц. Положения частиц, отмеченные точками, определены через равные промежутки времени – 30 с. Эти точки соединены прямыми линиями. В действительности траектория частиц гораздо сложнее.
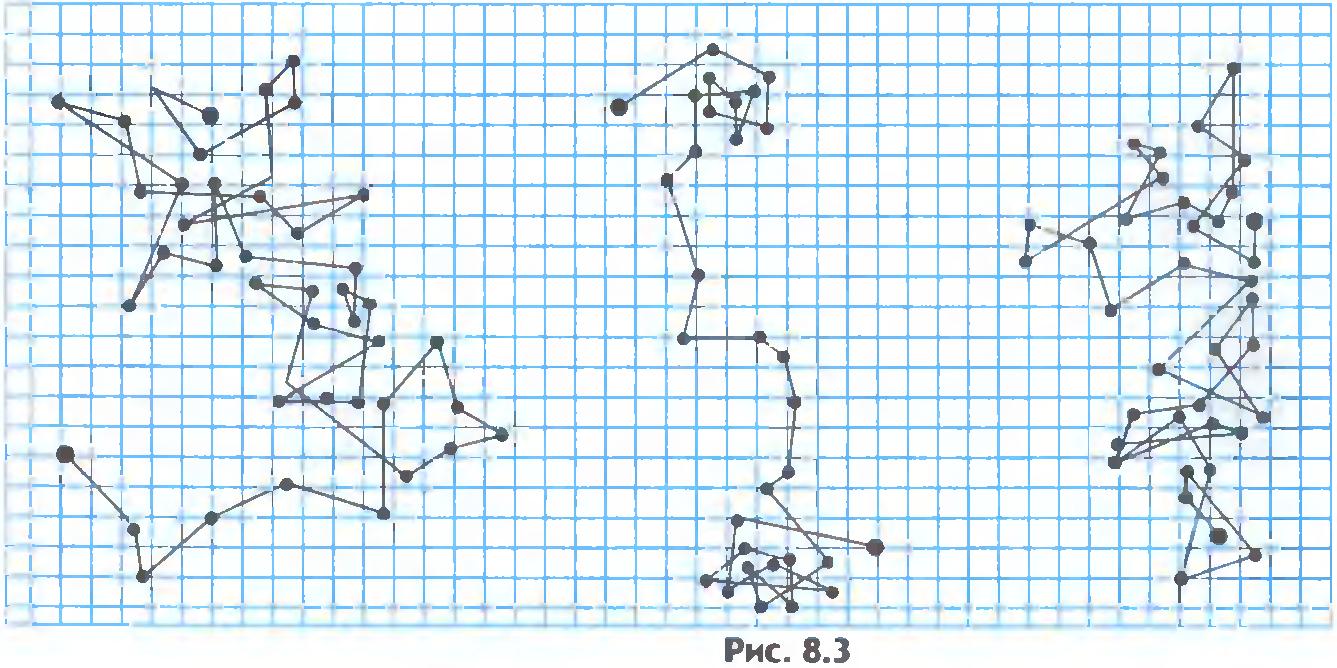
Броуновское движение можно наблюдать и в газе. Его совершают взвешенные в воздухе частицы пыли или дыма.
Красочно описывает броуновское движение немецкий физик Р. Поль (1884-1976): «Немногие явления способны так увлечь наблюдателя, как броуновское движение. Здесь наблюдателю позволяется заглянуть за кулисы того, что совершается в природе. Перед ним открывается новый мир – безостановочная сутолока огромного числа частиц. Быстро пролетают в поле зрения микроскопа мельчайшие частицы, почти мгновенно меняя направление движения. Медленнее продвигаются более крупные частицы, но и они постоянно меняют направление движения. Большие частицы практически толкутся на месте. Их выступы явно показывают вращение частиц вокруг своей оси, которая постоянно меняет направление в пространстве. Нигде нет и следа системы или порядка. Господство слепого случая – вот какое сильное, подавляющее впечатление производит эта картина на наблюдателя».
В настоящее время понятие броуновское движение используется в более широком смысле. Например, броуновским движением является дрожание стрелок чувствительных измерительных приборов, которое происходит из-за теплового движения атомов деталей приборов и окружающей среды.
Объяснение броуновского движения
Объяснить броуновское движение можно только на основе молекулярно-кинетической теории. Причина броуновского движения частицы заключается в том, что удары молекул жидкости о частицу не компенсируют друг друга. На рисунке 8.4 схематически показано положение одной броуновской частицы и ближайших к ней молекул. При беспорядочном движении молекул передаваемые ими броуновской частице импульсы, например слева и справа, неодинаковы. Поэтому отлична от нуля результирующая сила давления молекул жидкости на броуновскую частицу. Эта сила и вызывает изменение движения частицы.
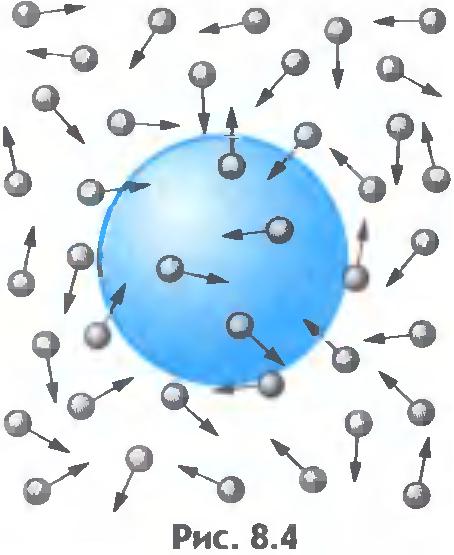
Среднее давление имеет определенное значение как в газе, так и в жидкости. Но всегда происходят незначительные случайные отклонения от этого среднего значения. Чем меньше площадь поверхности тела, тем заметнее относительные изменения силы давления, действующей на данную площадь. Так, например, если площадка имеет размер порядка нескольких диаметров молекулы, то действующая на нее сила давления меняется скачкообразно от нуля до некоторого значения при попадании молекулы в эту площадку.
Молекулярно-кинетическая теория броуновского движения была создана в 1905 г. А. Эйнштейном (1879-1955).
Построение теории броуновского движения и ее экспериментальное подтверждение французским физиком Ж. Перреном окончательно завершили победу молекулярно-кинетической теории.
Опыты Перрена
Идея опытов Перрена состоит в следующем. Известно, что концентрация молекул газа в атмосфере уменьшается с высотой. Если бы не было теплового движения, то все молекулы упали бы на Землю и атмосфера исчезла бы. Однако если бы не было притяжения к Земле, то за счет теплового движения молекулы покидали бы Землю, так как газ способен к неограниченному расширению. В результате действия этих противоположных факторов устанавливается определенное распределение молекул по высоте, о чем сказано выше, т. е. концентрация молекул довольно быстро уменьшается с высотой. Причем, чем больше масса молекул, тем быстрее с высотой убывает их концентрация.
Броуновские частицы участвуют в тепловом движении. Так как их взаимодействие пренебрежимо мало, то совокупность этих частиц в газе или жидкости можно рассматривать как идеальный газ из очень тяжелых молекул. Следовательно, концентрация броуновских частиц в газе или жидкости в поле тяжести Земли должна убывать по тому же закону, что и концентрация молекул газа. Закон этот известен.
Перрен с помощью микроскопа большого увеличения и малой глубины поля зрения (малой глубины резкости) наблюдал броуновские частицы в очень тонких слоях жидкости. Подсчитывая концентрацию частиц на разных высотах, он нашел, что эта концентрация убывает с высотой по тому же закону, что и концентрация молекул газа. Отличие в том, что за счет большой массы броуновских частиц убывание происходит очень быстро.
Более того, подсчет броуновских частиц на разных высотах позволил Перрену определить постоянную Авогадро совершенно новым методом. Значение этой постоянной совпало с известным.
Все эти факты свидетельствуют о правильности теории броуновского движения и, соответственно, о том, что броуновские частицы участвуют в тепловом движении молекул.
Вы наглядно убедились в существовании теплового движения; увидели, как происходит беспорядочное движение. Молекулы движутся еще более беспорядочно, чем броуновские частицы.
Сущность явления
Теперь давайте попробуем разобраться в сущности явления броуновского движения. А происходит оно потому, что все абсолютно жидкости и газы состоят из атомов или молекул. Но также нам известно, что эти мельчайшие частицы, находясь в непрерывном хаотическом движении, постоянно толкают броуновскую частицу с разных сторон.
Но вот что интересно, ученые доказали, что частицы более крупных размеров, которые превышают 5 мкм остаются неподвижными и в броуновском движении почти не участвуют, чего не скажешь о более мелких частицах. Частицы, имеющие размер менее 3 мкм, способны двигаться поступательно, совершая вращения или выписывая сложные траектории.
При погружении в среду крупного тела, происходящие в огромном количестве толчки, как бы выходят на средний уровень и поддерживают постоянное давление. В этом случае в действие вступает теория Архимеда, так как окруженное средой со всех сторон крупное тело уравновешивает давление и оставшаяся подъемная сила позволяет этому телу всплыть, или утонуть.
Но если тело имеет размеры такие, как броуновская частица, то есть совершенно незаметные, то становятся заметны отклонения давления, которые способствуют созданию случайной силы, которая приводит к колебаниям этих частиц. Можно сделать вывод, что броуновские частицы в среде находятся во взвешенном состоянии, в отличие от больших частиц, которые тонут или всплывают.
Значение броуновского движения
Давайте попробуем разобраться, имеет ли какое-либо значение броуновское движение в природной среде:
• Во-первых, броуновское движение играет значительную роль в питании растений из почвы;
• Во-вторых, в организмах человека и животных всасывание питательных веществ происходит через стенки органов пищеварения благодаря броуновскому движению;
• В-третьих, в осуществлении кожного дыхания;
• Ну и последнее, имеет значение броуновское движение и в распространении вредных веществ в воздухе, и в воде.
Домашнее задание
Внимательно прочитайте вопросы и дайте письменные ответы на них:
1. Вспомните, что называется диффузией?
2. Какая существует связь между диффузией и тепловым движением молекул?
3. Дайте определение броуновскому движению.
4. Как вы думаете, является ли броуновское движение тепловым, и обоснуйте свой ответ?
5. Изменится ли характер броуновского движения при нагревании? Если изменится, то, как именно?
6. Каким прибором пользуются при изучении броуновского движения?
7. Меняется ли картина броуновского движения при увеличении температуры и как именно?
8. Произойдут ли какие-либо изменения в броуновском движении, если водную эмульсию заменить на глицериновую?
Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс
Броуновское движение


Средняя оценка: 4.3
Всего получено оценок: 147.
Средняя оценка: 4.3
Всего получено оценок: 147.
Броуновское движение – хаотичное движение мельчайших видимых частиц твердого вещества в газе или жидкости. Так в чем суть, и чем обусловлено броуновское движение частиц?
Открытие броуновского движения
В 1827 году ботаник Роберт Броун наблюдал за движением пыльцевых зерен в жидкости. Он обнаружил, что эти мельчайшие частицы безостановочно и хаотично движутся в воде. Этот случай его очень удивил, первой его реакцией было высказывание о том, что, наверное, пыльца живая, раз может двигаться. Поэтому тот же опыт он проделал с неорганическими веществами. И уже на основе этого примера выяснил, что частицы определенных размеров, независимо от того, органические они или неорганические, движутся хаотично и безостановочно в жидкостях и газе.
Уже позже было установлено, что в зависимости от размера частицы участвуют или не участвуют в броуновском движении. Если размер частицы более 5 мкм, то эти частицы в броуновском движении практически не участвуют. Если размер частиц менее 3 мкм, то эти частицы движутся хаотично, поступательно, либо вращаются.
Броуновские частицы в водной среде обычно не тонут, но и не всплывают на поверхность. Они находятся в толще жидкости во взвешенном состоянии
Уже в XIX веке броуновское движение изучал французский физик Луи Жорж Гуи. Он установил, что чем меньше внутреннее трение жидкости, тем броуновское движение становится интенсивнее.
 Рис. 2. Портрет Луи Жорж Гуи.
Рис. 2. Портрет Луи Жорж Гуи.
Броуновское движение не зависит от освещения и внешнего электромагнитного поля. Оно вызвано влиянием теплового движения молекул.
Общая характеристика броуновского движения
Броуновское движение имеет место быть, так как все жидкости и газы состоят из атомов и молекул, которые постоянно находятся в движении. Следовательно, броуновская частица, попадая в жидкую или газообразную среду, подвергается воздействию этих атомов и молекул, которые двигают и толкают ее.
Когда в жидкую или газообразную среду помещено крупное тело, то толчки формируют постоянное давление. Если же среда окружает крупное тело со всех сторон, то давление уравновешивается, и на тело действует только сила Архимеда. Такое тело либо всплывает, либо тонет.
 Рис. 3. Броуновское движение пример.
Рис. 3. Броуновское движение пример.
Основной физический принцип лежащий в основе законов броуновского движения заключается в том, что средняя кинетическая энергия движения молекул жидкого или газообразного вещества равна средней кинетической энергии любой частицы, подвешенной в этой среде. Поэтому среднюю кинетическую энергию $E$ поступательного движения броуновской частицы можно вычислить по формуле: $E =
Броуновское движение объясняется тем, что благодаря случайной неодинаковости количества ударов молекул жидкости о частицу с разных направлений возникает равнодействующая сила определенного направления.

Что мы узнали?
Броуновское движение – бесконечное и хаотичное движение частиц определенного размера в газе или жидкости, молекулы и атомы которых приводят в движение эти частицы. В данной статье дается определение броуновского движения, а также объясняются причины его возникновения.
Броуновское движение в физике
Содержание:
Определение
Броуновским движением называется хаотическое и беспорядочное движение маленьких частиц, как правило, молекул в разных жидкостях или газах. Причиной возникновения броуновского движения является столкновение одних (более мелких частиц) с другими частицами (уже более крупными). Какая история открытия броуновского движения, его значение в физике, и в частности в атомно-молекулярной теории? Какие примеры броуновского движения есть в реальной жизни? Обо всем этом читайте далее в нашей статье.
Открытие
Первооткрывателем броуновского движения был английский ботаник Роберт Броун (1773-1858), собственно именно в его честь оно и названо «броуновским». В 1827 году Роберт Броун занимался активными исследованиями пыльцы разных растений. Особенно сильно его интересовало, то, какое участие пыльца принимает в размножении растений. И вот как то, наблюдая в микроскоп движение пыльцы в овощном соке, ученый заметил, что мелкие частицы то и дело совершают случайные извилистые движения.
Наблюдение Броуна подтвердили и другие ученые. В частности было подмечено, что частицы имеют свойство ускоряться с увеличением температуры, а также с уменьшением размера самих частиц. А при увеличении вязкости среды, в которой они находились, их движение наоборот, замедлялось.

Роберт Броун, открыватель броуновского движения.
Сначала Роберт Броун подумал, что он наблюдает движение, даже «танец» каких-то живых микроорганизмов, ведь и сама пыльца – это, по сути, мужские половые клетки растений. Но похожее движение имели и частицы мертвых растений, и даже растений засушенных сто лет назад в гербариях. Еще больше удивился ученый, когда стал исследовать неживую материю: мелкие частицы угля, сажи, и даже частички пыли лондонского воздуха. Затем под микроскоп исследователя попало стекло, различные и разнообразные минералы. И везде были замечены эти «активные молекулы», пребывающие в постоянном и хаотичном движении.
Это интересно: вы и сами можете наблюдать броуновское движение своими глазами, для этого вам понадобится не сильный микроскоп (ведь во время жизни Роберта Броуна еще не было мощных современных микроскопов). Если рассматривать через этот микроскоп, например, дым в зачерненной коробке и освещенный боковым лучом света, то можно будет увидеть маленькие кусочки сажи и пепла, которые будут непрерывно скакать туда-сюда. Это и есть броуновское движение.
Атомно-молекулярная теория
Открытое Броуном движение вскоре стало очень известным в научных кругах. Сам первооткрыватель с удовольствием показывал его многим своим коллегам. Однако долгие годы и сам Роберт Броун, ни его коллеги не могли объяснить причины возникновения броуновского движения, то почему оно вообще происходит. Тем более что броуновское движение было совершенно беспорядочным и не поддавалось никакой логике.
Его пояснение было дано лишь в конце ХIX века и оно не сразу было принято научным сообществом. В 1863 году немецкий математик Людвиг Кристиан Винер предположил, что броуновское движение обусловлено колебательными движениями неких невидимых атомов. По сути это было первое объяснение этого странного явления, связанное со свойствами атомов и молекул, первая попытка при помощи броуновского движения проникнуть в тайну строения материи. В частности Винер попытался измерить зависимость скорости движения частиц от их размера.
Впоследствии идеи Винера были развиты другими учеными, среди них был известный шотландский физик и химик Уильям Рамзай. Именно ему удалось доказать, что причиной броуновского движения мелких частиц являются удары на них еще более мелких частиц, которые в обычный микроскоп уже не видны, подобно тому, как не видны с берега волны качающие далекую лодку, хотя движение самой лодки видно вполне ясно.

Уильям Рамзай в своей лаборатории.
Таким образом броуновское движение стало одной из составных частей атомно-молекулярной теории и одновременно важным доказательством того факта, что вся материя, состоит из мельчайших частиц: атомов и молекул. В это трудно поверить, но еще в начале ХХ века часть ученых отрицала атомно-молекулярную теорию, и не верила в существование молекул и атомов. Научные работы Рамзая связанные с броуновским движением нанесли сокрушительный удар противникам атомизма, и заставили всех ученых окончательно убедиться, что вот смотрите сами, атомы и молекулы существуют, и их действие можно видеть собственным глазами.
Теория броуновского движения
Несмотря на внешний беспорядок хаотического движения частиц, их случайные перемещения все-таки попытались описать математическими формулами. Так родилась теория броуновского движения.
К слову, одним из тех, кто разрабатывал эту теорию, был польский физик и математик Мариан Смолуховский, который как раз в то время работал во Львовском университете и жил в родном городе автора этой статьи, в прекрасном украинском городе Львове.

Львовский университет, ныне университет им. И. Франка.
Параллельно с Смолуховским теорией броуновского движения занимался один из светочей мировой науки – знаменитый Альберт Эйнштейн, который в то время еще был молодым и никому известным работником в Патентном бюро швейцарского города Берна.

Оба ученых в результате создали свою теорию, которую можно также называть теорией Смолуховского-Эйнштейна. В частности была сформирована математическая формула, согласно нее среднее значение квадрата смещения броуновской частицы (s 2 ) за время t прямо пропорционально температуре Т и обратно пропорционально вязкости жидкости n, размеру частицы r и постоянной Авогадро.
NA: s 2 = 2RTt/6 ph rNA – так выглядит эта формула.
R в формуле – газовая постоянная. Так, если за 1 мин частица диаметром 1 мкм сместится на 10 мкм, то за 9 мин – на 10 = 30 мкм, за 25 мин – на 10= 50 мкм и т.д. В аналогичных условиях частица диаметром 0,25 мкм за те же отрезки времени (1, 9 и 25 мин) сместится соответственно на 20, 60 и 100 мкм, так как = 2. Важно, что в приведенную формулу входит постоянная Авогадро, которую таким образом, можно определить путем количественных измерений перемещения броуновской частицы, что и сделал французский физик Жан Батист Перрен.
Для наблюдений за броуновскими частицами Перрен использовал новейший на то время ультрамикроскоп, через который уже были видны мельчайшие частицы вещества. В своих опытах ученый, вооружившись секундомером, отмечал положения тех или иных броуновских частиц через равные интервалы времени (например, через 30 секунд). Затем соединяя положения частиц прямыми линями, получались разнообразные замысловатые траектории их движения. Все это зарисовывались на специальном разграфленном листе.
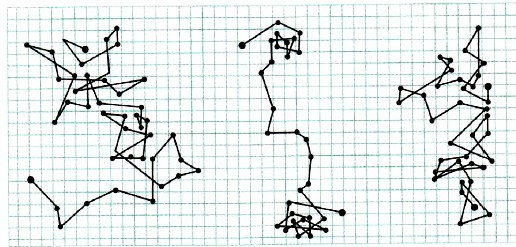
Так выглядели эти рисунки.
Составляя теоретическую формулу Эйнштейна со своими наблюдениями Перрен смог получить максимально точное для того времени значение числа Авогадро: 6,8 . 10 23
Своими опытами он подтвердил теоретические выводы Эйнштейна и Смолуховского.
Диффузия
Перемещения частиц при броуновском движении, внешне очень похоже с движением частиц при диффузии – взаимному проникновению молекул разных веществ под действием температуры. Тогда в чем же различие между броуновским движением и диффузией? В действительности, и диффузия и броуновское движение происходят по причине хаотического теплового движения молекул, и как результат описываются похожими математическими правилами.
Разница между ними в том, что при диффузии молекула всегда движется по прямой линии, пока не столкнется с другой молекулой, после чего она изменит траекторию своего движения. Броуновская частица «свободного полета» не совершает, а испытывает очень мелкие и частые как бы «дрожания», вследствие которых она хаотически перемещается то туда, то сюда. Говоря образным языком, броуновская частица подобна пустой банки пива, валяющейся на площади, где собралась большая толпа народу. Люди снуют туда-сюда, задевают банку своими ногами и она летает хаотически в разные стороны подобно броуновской частице. А движение самих людей в толпе уже более характерно для движения частиц при диффузии.
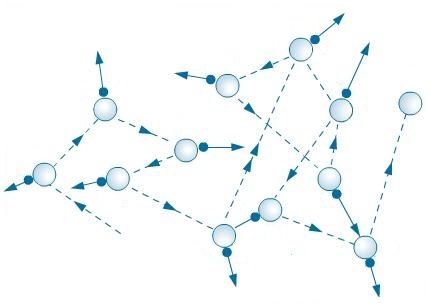
Если же смотреть на микро уровне, то причиной движения броуновской частицы является ее столкновение с более мелкими частицами, в то время как при диффузии частицы сталкиваются с себе подобными другими частицами.
И диффузия и броуновское движение происходит под действием температуры. С уменьшением температуры, как скорость частиц при броуновском движении, так и скорость движения частиц при диффузии замедляются.
Примеры в реальной жизни
Теория броуновского движения, этих случайных блужданий имеет и практическое воплощение в нашей реальной жизни. Например, почему, человек, который заблудился в лесу, периодически возвращается на одно и то же место? Потому, что он ходит не кругами, а примерно так, как движется обычно броуновская частица. Поэтому свой собственный путь он пересекает сам много раз.
Поэтому, не имея четких ориентиров и направлений движения, заблудившийся человек уподобляется броуновской частице, совершающей хаотические движения. Но чтобы выйти из леса нужно иметь четкие ориентиры, разработать систему, вместо того, чтобы совершать разные бессмысленные действия. Одним словом, не стоит вести себя в жизни подобно броуновской частице, бросаясь из стороны в сторону, а знать свое направление, цель и призвание, иметь мечты, смелость и упорство их достигать. Вот так из физики мы плавно перешли к философии. На этом заканчиваем эту статью.
Видео
И в завершение образовательное видео по теме нашей статьи.
Автор: Павел Чайка, главный редактор журнала Познавайка
При написании статьи старался сделать ее максимально интересной, полезной и качественной. Буду благодарен за любую обратную связь и конструктивную критику в виде комментариев к статье. Также Ваше пожелание/вопрос/предложение можете написать на мою почту pavelchaika1983@gmail.com или в Фейсбук, с уважением автор.
Эта статья доступна на английском языке – Brownian Motion.
Броуновское движение в физике – определение, в чем суть и примеры
Бро́уновское движе́ние — в естествознании, беспорядочное движение микроскопических, видимых, взвешенных в жидкости (или газе) частиц (броуновские частицы) твёрдого вещества (пылинки, крупинки взвеси, частички пыльцы растения и так далее), вызываемое тепловым движением частиц жидкости (или газа). Не следует смешивать понятия «броуновское движение» и «тепловое движение»: броуновское движение является следствием и свидетельством существования теплового движения.
Сущность явления
Броуновское движение происходит из-за того, что все жидкости и газы состоят из атомов или молекул — мельчайших частиц, которые находятся в постоянном хаотическом тепловом движении, и потому непрерывно толкают броуновскую частицу с разных сторон. Было установлено, что крупные частицы с размерами более 5 мкм в броуновском движении практически не участвуют (они неподвижны или седиментируют),более мелкие частицы (менее 3мкм) двигаются поступательно по весьма сложным траекториям или вращаются. Когда в среду погружено крупное тело, то толчки, происходящие в огромном количестве, усредняются и формируют постоянное давление. Если крупное тело окружено средой со всех сторон, то давление практически уравновешивается, остаётся только подъёмная сила Архимеда — такое тело плавно всплывает или тонет. Если же тело мелкое, как броуновская частица, то становятся заметны флуктуации давления, которые создают заметную случайно изменяющуюся силу, приводящую к колебаниям частицы. Броуновские частицы обычно не тонут и не всплывают, а находятся в среде во взвешенном состоянии.
Открытие броуновского движения
Это явление открыто Р. Броуном в 1827 году, когда он проводил исследования пыльцы растений. Шотландский ботаник Роберт Броун (иногда его фамилию транскрибируют как Браун) еще при жизни как лучший знаток растений получил титул «князя ботаников». Он сделал много замечательных открытий. В 1805 после четырехлетней экспедиции в Австралию привез в Англию около 4000 видов не известных ученым австралийских растений и много лет потратил на их изучение. Описал растения, привезенные из Индонезии и Центральной Африки. Изучал физиологию растений, впервые подробно описал ядро растительной клетки. Петербургская Академия наук сделала его своим почетным членом. Но имя ученого сейчас широко известно вовсе не из-за этих работ.
В 1827 Броун проводил исследования пыльцы растений. Он, в частности, интересовался, как пыльца участвует в процессе оплодотворения. Как-то он разглядывал под микроскопом выделенные из клеток пыльцы североамериканского растения Clarkia pulchella (кларкии хорошенькой) взвешенные в воде удлиненные цитоплазматические зерна. Неожиданно Броун увидел, что мельчайшие твердые крупинки, которые едва можно было разглядеть в капле воды, непрерывно дрожат и передвигаются с места на место. Он установил, что эти движения, по его словам, «не связаны ни с потоками в жидкости, ни с ее постепенным испарением, а присущи самим частичкам».
Наблюдение Броуна подтвердили другие ученые. Мельчайшие частички вели себя, как живые, причем «танец» частиц ускорялся с повышением температуры и с уменьшением размера частиц и явно замедлялся при замене воды более вязкой средой. Это удивительное явление никогда не прекращалось: его можно было наблюдать сколь угодно долго. Поначалу Броун подумал даже, что в поле микроскопа действительно попали живые существа, тем более что пыльца – это мужские половые клетки растений, однако так же вели частички из мертвых растений, даже из засушенных за сто лет до этого в гербариях. Тогда Броун подумал, не есть ли это «элементарные молекулы живых существ», о которых говорил знаменитый французский естествоиспытатель Жорж Бюффон (1707–1788), автор 36-томной Естественной истории. Это предположение отпало, когда Броун начал исследовать явно неживые объекты; сначала это были очень мелкие частички угля, а также сажи и пыли лондонского воздуха, затем тонко растертые неорганические вещества: стекло, множество различных минералов. «Активные молекулы» оказались повсюду: «В каждом минерале, – писал Броун, – который мне удавалось измельчить в пыль до такой степени, чтобы она могла в течение какого-то времени быть взвешенной в воде, я находил, в больших или меньших количествах, эти молекулы».
Теория броуновского движения
Построение классической теории
В 1905 году Альбертом Эйнштейном была создана молекулярно-кинетическая теория для количественного описания броуновского движения. В частности, он вывел формулу для коэффициента диффузии сферических броуновских частиц:

где D — коэффициент диффузии, R — универсальная газовая постоянная, T — абсолютная температура , NA — постоянная Авогадро, a — радиус частиц, ξ — динамическая вязкость.
Броуновское движение
Вы будете перенаправлены на Автор24
Что такое Броуновское движение
Броуновским движением называют непрерывное хаотическое движение малых частиц, взвешенных в жидкости или газе.
Это движение характеризуется следующими чертами:
- продолжается неограниченно долго без каких бы то ни было видимых изменений,
- интенсивность движения броуновских частиц зависит от их размеров, но не зависит от их природы,
- интенсивность возрастает с ростом температуры,
- интенсивность возрастает с уменьшением вязкости жидкости или газа.
Броуновское движение не является молекулярным движением, но служит непосредственным доказательством существования молекул и хаотического характера их теплового движения.
Сущность Броуновского движения
Сущность этого движения в следующем. Частица вместе с молекулами жидкости или газа образуют одну статистическую систему. В соответствии с теоремой о равномерном распределении энергии по степени свободы на каждую степень свободы приходится 1/2kT энергии. Энергия 2/3kT, приходящаяся на три поступательные степени свободы частицы, приводит к движению ее центра масс, которое наблюдается под микроскопом в виде дрожания частицы. Если броуновская частица достаточно жесткая, то еще 3/2kT энергии приходится на ее вращательные степени свободы. Поэтому при своем дрожании она испытывает еще и постоянные изменения ориентировки в пространстве.
Можно объяснить броуновское движение и так: причиной Броуновского движения являются флуктуации давления, которое оказывается на поверхность малой частицы со стороны молекул среды. Сила и давление изменяется по модулю и направлению, в результате чего частица находится в беспорядочном движении.
Движение броуновской частицы является случайным процессом. Вероятность (dw) того, что броуновская частица, находившаяся в однородной изотропной среде в начальный момент времени (t=0) в начале координат, сместится вдоль произвольно направленной (при t$>$0) оси Ox так, что ее координата будет лежать в интервале от x до x+dx, равна:
где $triangle x$- малое изменение координаты частицы, вследствие флуктуации.
Рассмотрим положение Броуновской частицы через некоторые фиксированные промежутки времени. Начало координат поместим в точку, в которой частица находилась при t=0. Обозначим $overrightarrow
Перемещения частицы происходит по сложной ломаной линии все время наблюдений.
Найдем средний квадрат удаления частицы от начала после n шагов в большой серии опытов:
где $leftlangle q^2_irightrangle $- средний квадрат смещения частицы на i- м шаге в серии опытов (он для всех шагов одинаков и равен какой-то положительной величине a2), $leftlangle q_iq_jrightrangle $- является средней величиной скалярного произведения при i-м шаге на перемещение при j-м шаге в различных опытах. Эти величины независимы друг от друга, одинаково часто встречаются как положительные значения скалярного произведения, так и отрицательные. Поэтому, считаем, что $leftlangle q_iq_jrightrangle $=0 при$ ine j$. Тогда имеем из (3):
[leftlangle r^2_nrightrangle =a^2n=frac
где $triangle t$- промежуток времени между наблюдениями; t=$triangle tn$ – время, в течение которого средний квадрат удаления частицы стал равен $leftlangle r^2rightrangle .$ Получаем, что частица удаляется от начала. Существенно то, что средний квадрат удаления растет пропорционально первой степени времени. $alpha $- можно найти экспериментально, а можно теоретически, как будет показано в примере 1.
Броуновская частица движется не только поступательно, но и вращаясь. Среднее значение угла поворота $triangle varphi $ броуновской частицы за время t равно:
где $D_
где $eta $ – коэффициент вязкости среды.
Броуновское движение ограничивает точность измерительных приборов. Предел точности зеркального гальванометра определяется дрожание зеркальца, подобно броуновской частице, которая подвергается ударам молекул воздуха. Случайное движение электронов вызывает шумы в электрических сетях.
Готовые работы на аналогичную тему
Задание: Для того, чтобы математически полно охарактеризовать броуновское движение, надо найти $alpha $ в формуле $leftlangle r^2_nrightrangle =alpha t$. Считать коэффициент вязкости жидкости известным и равным b, температура жидкости T.
Запишем уравнение движения броуновской частицы в проекции на ось Ox:
где m — масса частицы, $F_x$ — случайная сила, действующая на частицу, $bdot
Аналогичный вид имеют уравнения для величин, относящиеся к другим координатным осям.
Умножим обе части уравнения (1.1) на x, а члены $ddot
Тогда уравнение (1.1) приведем к виду:
Усредним обе части этого уравнения по ансамблю броуновских частиц, учитывая при этом, что средняя от производной по времени равна производной от средней величины, так как это усреднение по ансамблю частиц, и, значит, переставим операцией дифференцирования по времени. В результате усреднения (1.3) получаем:
[frac
Так как отклонения броуновской частицы в любом направлении равновероятны, то:
[leftlangle x^2rightrangle =leftlangle y^2rightrangle =leftlangle z^2rightrangle =frac
Используем $leftlangle r^2_nrightrangle =a^2n=frac
Из-за случайного характера силы $F_x$ и координаты частицы x и их независимости друг от друга должно выполняться равенство $leftlangle F_xxrightrangle =0$, тогда (1.5) сводится к равенству:
По теореме о равномерном распределении энергии по степеням свободы:
Таким образом, получим формулу для решения задачи о Броуновском движении:
[leftlangle r^2rightrangle =frac<6kT>t]
Ответ: Формула $leftlangle r^2rightrangle =frac<6kT>t$ решает задачу о броуновском движении взвешенных частиц.
Задание: Частицы гуммигута сферической формы радиуса r участвуют в броуновском движении в газе. Плотность гуммигута $rho $. Найти среднеквадратичную скорость частиц гуммигута при температуре T.
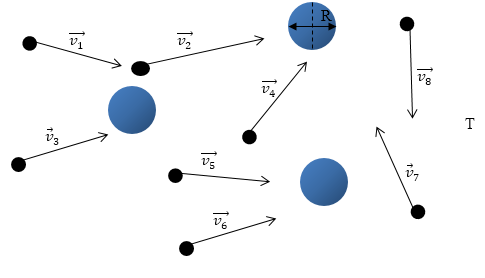
Среднеквадратичная скорость молекул равна:
[leftlangle v^2rightrangle =sqrt
Броуновская частица находится в равновесии с веществом, в котором она находится, и мы можем рассчитать ее среднеквадратичную скорость, используя формулу для скорости молекул газа, которые, в свою очередь, двигаясь, заставляют перемещаться броуновскую частицу. Для начала найдем массу частицы:
[m_0=rho V=frac<4><3>pi R^3rho left(2.2right)]
Ответ: Скорость частицы гуммигута взвешенного в газе можно найти как $leftlangle v^2rightrangle =sqrt
Электролиз расплавов и растворов
Теория к заданию 22 из ЕГЭ по химии
Электролиз расплавов и растворов (солей, щелочей)
Если в раствор или расплав электролита опустить электроды и пропустить постоянный электрический ток, то ионы будут двигаться направленно: катионы к катоду (отрицательно заряженному электроду), анионы к аноду (положительно заряженному электроду).
На катоде катионы принимают электроны и восстанавливаются, на аноде анионы отдают электроны и окисляются. Этот процесс называют электролизом.
Электролиз — это окислительно-восстановительный процесс, протекающий на электродах при прохождении электрического тока через расплав или раствор электролита.
Электролиз расплавленных солей
Рассмотрим процесс электролиза расплава хлорида натрия. В расплаве идет процесс термической диссоциации:
Под действием электрического тока катионы $Na^<+>$ движутся к катоду и принимают от него электроны:
Анионы $Cl^<->$ движутся к аноду и отдают электроны:
Суммарное уравнение процессов:
На катоде образуется металлический натрий, на аноде — газообразный хлор.
Главное, что вы должны помнить: в процессе электролиза за счет электрической энергии осуществляется химическая реакция, которая самопроизвольно идти не может.
Электролиз водных растворов электролитов
Более сложный случай — электролиз растворов электролитов.
В растворе соли, кроме ионов металла и кислотного остатка, присутствуют молекулы воды. Поэтому при рассмотрении процессов на электродах необходимо учитывать их участие в электролизе.
Для определения продуктов электролиза водных растворов электролитов существуют следующие правила:
1. Процесс на катоде зависит не от материала, из которого сделан катод, а от положения металла (катиона электролита) в электрохимическом ряду напряжений, при этом если:
1.1. Катион электролита расположен в ряду напряжений в начале ряда по $Al$ включительно, то на катоде идет процесс восстановления воды (выделяется водород $Н_2↑$). Катионы металла не восстанавливаются, они остаются в растворе.
1.2. Катион электролита находится в ряду напряжений между алюминием и водородом, то на катоде восстанавливаются одновременно и ионы металла, и молекулы воды.
1.3. Катион электролита находится в ряду напряжений после водорода, то на катоде восстанавливаются катионы металла.
1.4. В растворе содержатся катионы разных металлов, то сначала восстанавливается катион металла, стоящий в ряду напряжений правее.
Катодные процессы
| $Li K Ca Na Mg Al$ $Li^ <+>K^ <+>Ca^ <2+>Na^ <+>Mg^ <2+>Al^<3+>$ |
$Mn Zn Fe Ni Sn Pb$ $Mn^ <2+>Zn^ <2+>Fe^ <2+>Ni^ <2+>Sn^ <2+>Pb^<2+>$ |
$H_2$ $2H^<+>$ |
$Cu Hg Ag Pt Au$ $Cu^ <2+>Hg_2^ <2+>Ag^ <+>Pt^ <2+>Au^<3+>$ |
| Восстанавливается вода: $2H_2O+2ē=H_2↑+2OH^<−>;$ $M^ |
Восстанавливаются катионы металла и вода: $M^ $2H_2O+2ē=H_2↑+2OH^<−>$ |
Восстанавливаются катионы металла: $M^ |
|
| $nē→$ Усиление окислительных свойств катионов (способности принимать электроны) |
|||
2. Процесс на аноде зависит от материала анода и от природы аниона.
Анодные процессы
| Кислотный остаток $Ас^ |
Анод | |
| Растворимый | Нерастворимый | |
| Бескислородный | Окисление металла анода $M^<−>−nē=M^ анод раствор |
Окисление аниона (кроме $F^<–>$) $Ac^ |
| Кислородсодержащий | В кислотной и нейтральной средах: $2H_2O−4ē=O_2↑+4H^<+>$ В щелочной среде: $4OH^<−>−4ē=O_2↑+4H^<+>$ |
|
2.1. Если анод растворяется (железо, цинк, медь, серебро и все металлы, которые окисляются в процессе электролиза), то окисляется металл анода, несмотря на природу аниона.
2.2. Если анод не растворяется (его называют инертным — графит, золото, платина), то:
а) при электролизе растворов солей бескислородных кислот (кроме фторидов) на аноде идет процесс окисления аниона;
б) при электролизе растворов солей кислородсодержащих кислот и фторидов на аноде идет процесс окисления воды (выделяется $О_2↑$). Анионы не окисляются, они остаются в растворе;
в) анионы по их способности окисляться располагаются в следующем порядке:

Попробуем применить эти правила в конкретных ситуациях.
Рассмотрим электролиз раствора хлорида натрия в случае, если анод нерастворимый и если анод растворимый.
1) Анод нерастворимый (например, графитовый).
В растворе идет процесс электролитической диссоциации:
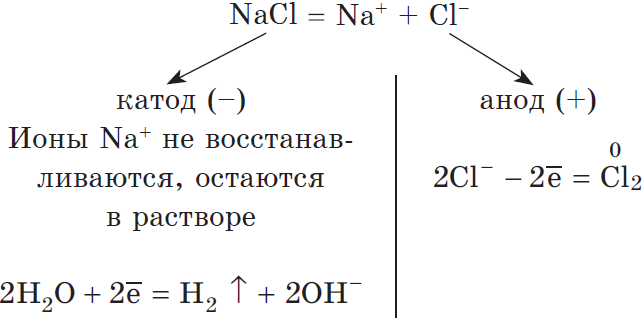
Учитывая присутствие ионов $Na^<+>$ в растворе, составляем молекулярное уравнение:
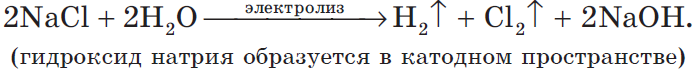
2) Анод растворимый (например, медный):
Если анод растворимый, то металл анода будет окисляться:
Катионы $Cu^<2+>$ в ряду напряжений стоят после ($Н^<+>$), по этому они и будут восстанавливаться на катоде.
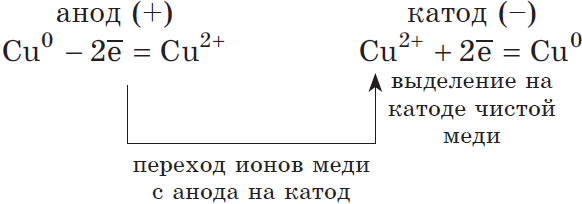
Концентрация $NaCl$ в растворе не меняется.
Рассмотрим электролиз раствора сульфата меди (II) на нерастворимом аноде:
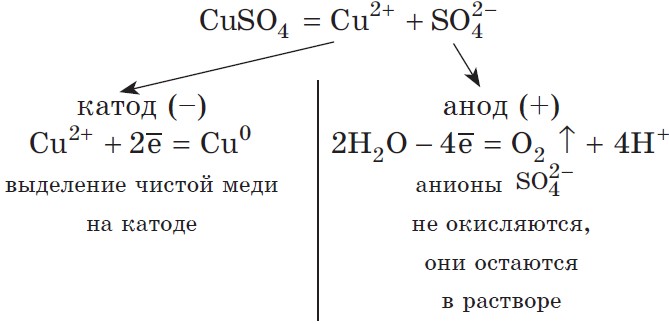
Суммарное ионное уравнение:
Суммарное молекулярное уравнение с учетом присутствия анионов $SO_4^<2->$ в растворе:
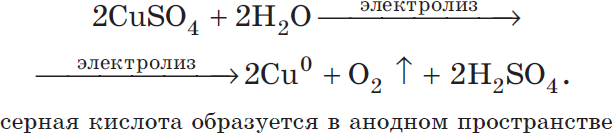
Рассмотрим электролиз раствора гидроксида калия на нерастворимом аноде:
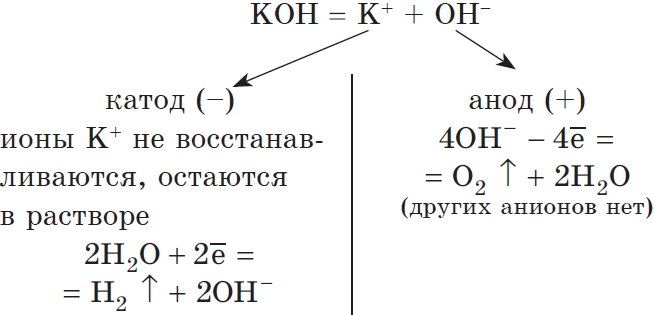
Суммарное ионное уравнение:
Суммарное молекулярное уравнение:
В данном случае, оказывается, идет только электролиз воды. Аналогичный результат получим и в случае электролиза растворов $H_2SO_4, NaNO_3, K_2SO_4$ и др.
Электролиз расплавов и растворов веществ широко используется в промышленности:
- Для получения металлов (алюминий, магний, натрий, кадмий получают только электролизом).
- Для получения водорода, галогенов, щелочей.
- Для очистки металлов — рафинирования (очистку меди, никеля, свинца проводят электрохимическим методом).
- Для защиты металлов от коррозии (хрома, никеля, меди, серебра, золота) — гальваностегия.
- Для получения металлических копий, пластинок — гальванопластика.





